III. LA GRAN PROEZA
| El problema de la gravitación me convirtió en un racionalista creyente, es decir, en alguien que busca la única fuente confiable de la verdad en la simplicidad matemática. Imagínate mi alegría al encontrar realizable la covariancia general y que las ecuaciones describen con precisión el corrimiento del perihelio de Mercurio. Estuve varios días fuera de mí de gozosa exaltación. A. EINSTEIN |
LA ESTANCIA de los Einstein en Zurich dura sólo 18 meses. Einstein
tiene ahí sus primeros estudiantes doctorales y usa parte de su tiempo para
desarrollar un aparato para medir pequeñas fluctuaciones —de tipo browniano—
de voltajes.1 Sin embargo, pronto recibe un nombramiento
de profesor titular —finalmente151 en la Universidad Alemana de Praga. Pese
a las dificultades de su carencia de religión y su ciudadanía suiza se confirma
el nombramiento y los Einstein se trasladan a Praga en marzo de 1911. Durante
su estancia allí —que también será muy breve— Einstein asiste al Primer
Congreso Solvay en noviembre de 1911. Mientras tanto, Marcel Grossmann (1878-1936)
—su cercano amigo y excompañero de estudios a quien Einstein dedicara su
tesis doctoral—, convertido en profesor de matemáticas en el ETH,
procura atraer a Einstein a su vieja escuela. Einstein ve con mucha simpatía
la invitación —e incluso declina por ella la oferta que le hace Lorentz
de convertirse en su sucesor en Leyden, puesto que ocupará más tarde Paul Ehrenfest
(1880-1933—. Finalmente, Einstein regresa a Zurich en agosto de 1912.
Ha dividido el tiempo entre problemas de diversa naturaleza, desde la mecánica estadística clásica hasta la desviación de la luz por la gravedad, aunque los problemas cuánticos son los que más le inquietan en este periodo. Sin embargo, ha avanzado considerablemente en su búsqueda de una generalización satisfactoria de la teoría de la relatividad. De regreso en Zurich se inicia una nueva y muy importante etapa en la construcción de la teoría de la relatividad general. Einstein induce a Grossmann a colaborar con él en la fundación de esta teoría; de esta colaboración, que tiene lugar durante los años de 1912 y 1913, emerge una nueva forma matemática de la teoría, la que está a la base de todos los desarrollos ulteriores, como veremos en la siguiente sección.
Tampoco la estancia en Zurich es larga, pues en 1913 Planck y Nernst visitan a Einstein en Zurich, para saber con qué interés consideraría una invitación a trabajar en Berlín, tal vez el centro más importante de la física de la época. La oferta es excepcional: se le nombraría miembro de la Academia Prusiana de Ciencias, se le daría un puesto de profesor en la Universidad de Berlín sin obligación de enseñar y se le ofrecía, además, la dirección del Instituto de Física Kaiser Wilhelm, que estaba por inaugurarse. Einstein vio aquí la oportunidad de liberarse de todas las cargas académicas que tanto le pesaban y aceptó. 2 Los Einstein se trasladan a Berlín en abril de 1914. Sin embargo, las relaciones con Mileva se habían deteriorado mucho en los años precedentes —básicamente por incompatibilidad de caracteres— y ella prefirió retornar con los niños a Zurich.
Es en Berlín donde Einstein da forma acabada a la teoría de la relatividad, en noviembre de 1915; pero no por ello abandona los problemas cuánticos, a los que dedica parte de su tiempo. La primera Guerra Mundial ha estallado, pero su nacionalidad suiza le permite continuar con sus labores. En 1916 publica su primer libro, Sobre la teoría especial y general de la relatividad, y en 1917 produce la primera cosmología relativista. Finalmente, el esfuerzo sostenido de los últimos años acaba por vencerlo y Einstein enferma seriamente de úlcera estomacal y del hígado en 1917. Su prima Elsa Einstein (18761936), recientemente enviudada y madre de dos hijas, Ilse y Margot, lo atiende y ayuda. La relación termina en matrimonio en 1919. Einstein pasa una breve temporada en 1919 en la Universidad de Zurich, pero declina las ofertas insistentes y conjuntas de esta universidad y el ETH de retornar a esta ciudad. Este es el año de la coronación de Einstein: con la oportuna ayuda de un eclipse, Einstein se transforma, al terminar la guerra, en el científico más famoso de todos los tiempos.
Cuando Einstein publicó su trabajo Fundamentos de la teoría general de la relatividad en 1916, el gran físico alemán Max Born (1882-1970) lo calificó como "la mayor proeza de la reflexión del hombre sobre la naturaleza; la más sorprendente combinación de penetración filosófica, intuición física y capacidad matemática". Einstein dedicó a esta proeza esfuerzos —que el mismo llegó a calificar de sobrehumanos en cartas a sus amigos— prácticamente ininterrumpidos desde 1911 hasta 1915, además del trabajo desarrollado a partir de 1907. Del principio de equivalencia de 1907 a la formulación final de 1915 hay una distancia enorme, que condujo a la teoría por rutas absolutamente nuevas para la física. Durante todos estos años, nadie fuera de Einstein se interesaba en esta teoría; para nadie tenía sentido este esfuerzo, pues no había nada que lo demandara. Una vez más encontramos a Einstein en una empresa solitaria. Y la firme guía que le conducía, capaz de permitirle realizar este tenaz y agotador esfuerzo, era sólo la profunda y muy íntima convicción de la necesidad lógica de esta teoría. No sólo era necesario generalizar el principio de la relatividad a todo tipo de movimiento, sino que era claro que la ley de la gravitación universal de Newton es una ley empírica, no deducida de primeros principios y que presupone, además, simultaneidad absoluta y acción a distancia. Seguramente era posible construir una teoría lógicamente simple, que fuera capaz de eliminar todas estas y muchas otras insuficiencias conceptuales y reflejara más fielmente la unidad intrínseca de la naturaleza.
El nuevo punto nodal que separa la forma inicial de la final de la teoría general tal vez se pueda encontrar en los trabajos realizados en Praga. Esencialmente, la consideración novedosa es ésta. Partimos de la convicción de que es tan natural demandar la validez del principio de relatividad para velocidades uniformes como para aceleraciones uniformes. Consideremos entonces su aplicación a un cuerpo que gira uniformemente; la contracción relativista de las distancias —la llamada contracción de Lorentz y que discutimos en el capítulo anterior— hace que la circunferencia cambie con el movimiento, pero no así el diámetro, que es perpendicular a la velocidad. Por lo tanto, el cociente entre estas cantidades deja de ser igual a p 3 ¡y pasa a depender de la velocidad! Esto significa que el sistema ya no satisface los principios de la geometría euclideana. La conclusión es inmediata: la elaboración de una teoría general de la relatividad requiere abandonar la geometría euclideana o, en palabras más llanas: espacio en que ocurren los fenómenos físicos no cumple las leyes de tal geometría. En sí misma, esta conclusión no es enteramente sorprendente, pues aunque los axiomas de la geometría euclideana han sido inspirados por la observación de lo que pasa en el mundo real y tienen por lo tanto un origen empírico, nada garantiza que entre la geometría así construida y el mundo material tenga que existir un paralelismo absoluto, pudiéndose dar desviaciones en condiciones apropiadas, por ejemplo, a escala cósmica.
Con Grossmann a su lado, Einstein encontró la oportunidad de penetrar en el terreno de las geometrías no euclideanas, encontrando que una forma particular de ellas, elaborada por el gran matemático alemán Bernhard Riemann (1826-1866) más de cincuenta años antes, era especialmente adecuada para los propósitos de la relatividad. Cuando se dice, cómo es común oír, que el espacio es curvo de acuerdo a la relatividad, lo que se está implicando es que en una región del espacio en que hay campos gravitatorios no se cumplen las leyes de la geometría de Euclides, sino las de la geometría de Riemann.
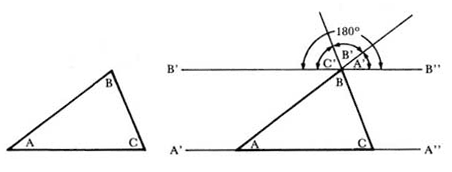
Figura 2. Los ángulos de un triángulo suman 180°. Los tres ángulos internos de un triángulo cualquiera se han denominado con las letras A, B y C. En la figura de la derecha se muestra el mismo triángulo y algunas rectas auxiliares; las rectas A´ A´´ y B´ B´´ son paralelas. Aplicando algunas reglas sencillas de la geometría comprobamos que los ángulos A´, B´, y C´ son iguales a los ángulos A, B y C, respectivamente; luego A+B+C=A´+B´+C´=180°.
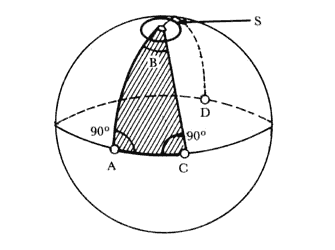
Figura 3. Un ejemplo de geometría no euclideana. La figura achurada es un triángulo esférico, construido sobre la superficie de una esfera, sin salirse de ella. La curva S encierra un círculo muy pequeño alrededor del Polo Norte: se observa que está constituido casi sobre un plano, por lo que cumple muy aproximadamente las leyes de la geometría euclideana. Pero la circunferencia sobre el ecuador ACDA tiene como diámetro al arco ABD, que mide media circunferencia, por lo que el cociente circunferencia/diámetro vale 2, resultado muy diferente de p .
La geometría euclideana es la que se obtiene operando con barras rígidas en un plano. Una construcción típica de esta geometría se representa en la figura 2 (a), que muestra un triángulo con ángulos internos A, B y C; la figura 2 (b) nos permite demostrar que la suma de los tres ángulos es siempre igual a 180°. Este resultado constituye un típico teorema de la geometría euclideana. 4 Por lo tanto, para saber si esta geometría se cumple o no en la realidad, todo lo que tenemos que hacer es construir un gran triángulo y medir sus tres ángulos internos para ver si suman 180° o no. Si hacemos el experimento sobre una hoja de papel, pronto nos convenceremos de que la geometría de Euclides se aplica. Pero de lo anterior se infiere que si hiciéramos este experimento a escala cósmica trazando el triángulo, por ejemplo, con haces de luz que los campos gravitatorios curvarían, el resultado sería diferente.
Una forma simple de visualizar la geometría de Riemann se obtiene al pensar en las relaciones geométricas que ocurren en la superficie de una esfera sin abandonar nunca la superficie. Así, una recta sobre la esfera es un arco de círculo máximo (es decir, cuyo plano pasa por el centro de la esfera). Tomemos ahora el pequeño círculo trazado sobre la esfera muy cerca del Polo Norte, e indicado como S en la figura 3; si el círculo es suficientemente pequeño se encuentra prácticamente sobre un plano y se aplica la geometría de Euclides; luego la razón de su circunferencia a su diámetro es p. Sin embargo, tomemos como circunferencia al ecuador, ACDA; el diámetro es la "recta" ABD que es igual a media circunferencia, según se ve en la misma figura 3. Luego, en este caso, la razón de la circunferencia al diámetro es 2. Vemos que para los seres bidimensionales que viven sobre una esfera la razón de la circunferencia al diámetro depende del tamaño del círculo y está comprendida entre 2 y 3.1415... Pero precisamente esto es lo que necesitamos en la relatividad: una relación no fija (que pueda depender de la velocidad y de los campos externos por el principio de equivalencia) y normalmente menor que p. Por esta razón la geometría de Riemann resultó apropiada para la teoría de la relatividad.
Veamos ahora qué sucede con un triángulo sobre la esfera, como el ilustrado en la misma figura 3, con ángulos A, B y C y achurado; por construcción, hemos hecho los ángulos en A y en C de 90º cada uno, es decir, trazados con perpendiculares al ecuador. De la figura es claro que podemos hacer el gajo achurado más o menos ancho, según deseemos; en particular, lo podemos tomar tan angosto que el ángulo en el vértice B se reduzca a cero. En este caso, la suma de los ángulos internos será de 90 + O + 90 =180°. Pero también podemos abrir el gajo tanto como sea posible; si le hacemos dar la vuelta completa, el ángulo en B aumenta hasta 360° y la suma de los tres ángulos resulta 90 + 360 + 90=540°s. Vemos que para los esferícolas el teorema del triángulo dice que la suma de los tres ángulos internos de un triángulo esta comprendida entre 180 y 540 grados. Este resultado nos ayuda a comprender qué tan diferente puede ser la geometría del mundo real de la geometría euclideana.
Acabamos de describir una de las propiedades más interesantes de la relatividad general. Vimos que en la teoría especial longitudes y tiempos dependen de la velocidad; ahora, más en general, vemos que dependen del movimiento acelerado, y, por lo tanto, de los campos en que se encuentran los cuerpos (por el principio de equivalencia). En esta forma, aun la estructura del espacio y el fluir del tiempo resultan depender de la materia que contiene dicho espacio, pues ella es la generadora de los campos (y los movimientos). Todo esto conduce a efectos que podemos medir, para verificar o falsificar la teoría. Veamos aunque sea muy brevemente los tres más famosos.
Vimos antes cómo desde 1907 Einstein notó que la teoría de la relatividad implica que la luz es desviada por la gravitación, pero consideró el efecto inobservable. En Praga corrigió esta última consideración, al notar que un haz de luz que pasa rasante por el disco solar, será desviado un ángulo pequeño, pero medible. Por lo tanto, una estrella que se encuentre muy cercana al Sol aparecerá ligeramente desviada de la posición que le atribuimos cuando el Sol se encuentra lejos (Figura 4). Einstein hizo ver que este fenómeno sería en principio observable durante un eclipse solar, pues al quedar tapada la luz directa del Sol podremos ver la estrella cercana al Sol y medir su desviación. El experimento se llevó a cabo, pero sobre de ello hablaremos más adelante.
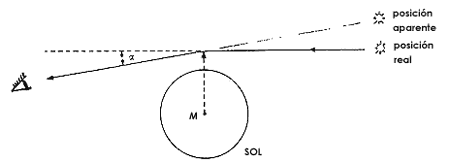
Figura 4. Desviación de un rayo luminoso por el Sol. Al desviar el Sol un haz de luz rasante que viene de una estrella lejana, cambia la posición aparente de está. El fenómeno se puede observar cuando la Luna oculta al Sol y obscurece el cielo. La figura está considerablemente exagerada (el ángulo a de desviación producido por el Sol es aproximadamente de 1/2000 de grado).
Un segundo efecto significativo predicho por la relatividad general, y que también ya hemos mencionado, es el que se refiere al corrimiento de la luz hacia el rojo debido a la acción de campos gravitatorios intensos. En 1925 este efecto fue observado por el astrónomo norteamericano Walter Adams en una estrella enana blanca (que es un tipo de estrella muy pequeña, pero muy masiva, por lo que posee un campo gravitatorio mucho más intenso que el solar), mientras que el correspondiente efecto producido por el Sol, mucho más débil, se logró observar durante la década de los sesentas.5
Lo que más entusiasmó a Einstein de su teoría general fue, sin embargo, otro aspecto. Al aplicar la teoría al caso del sistema planetario, observó que en vez de la órbitas elípticas que predice la teoría de Newton, la relatividad produce una especie de rosetas, es decir, elipses cuyo eje va girando con, el tiempo (Figura 5). La rotación del eje predicha por la teoría es muy pequeña, pero resultó ser exactamente la necesaria para resolver un problema centenario. Desde Kepler se sabe que los planetas describen órbitas elípticas alrededor del Sol; con la teoría de la gravedad de Newton fue posible calcular no sólo estas órbitas, sino incluso las desviaciones —en general muy pequeñas— que deben ocurrir debido a la constante perturbación que los otros cuerpos celestes, como los grandes planetas, producen. Los cálculos dieron resultados excelentes; los cielos se mueven conforme a las leyes de Newton. Sólo había una excepción: Mercurio, el pequeño planeta más próximo al Sol, tenía una órbita que se desviaba, lenta pero sistemáticamente, de lo calculado.6
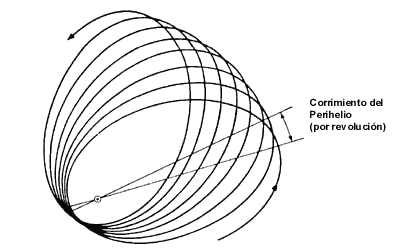
Figura 5. Precesión del perihelio de un planeta. La teoría general de la relatividad predice que la elipse descrita por una órbita planetaria va girando muy lentamente en su plano, de tal manera que al completarse una vuelta, el eje mayor apunta en una dirección un poco diferente. En la figura se muestra el fenómeno en forma muy exagerada.
Esfuerzos se hicieron, durante casi dos siglos, para explicar este fenómeno, pero sin éxito. Cuando Einstein aplicó sus métodos al caso de Mercurio el misterio quedó aclarado: esta desviación observada a lo largo de los siglos no era otra cosa que la rotación del eje de la elipse predicha por la relatividad general —para los otros planetas del Sistema Solar la desviación es insignificante—. La coincidencia numérica fue excelente: después de todo, los cielos se mueven conforme a las leyes de Einstein.
Regresemos al tema de la desviación de la luz por la gravedad. Cuando Einstein aplicó su teoría final a este problema, obtuvo un resultado inesperado: la desviación resulta ser el doble de la que sus versiones anteriores indicaban. Es decir, aparecía la desviación puramente newtoniana, debida al "peso" de la luz, pero también otra de igual magnitud y puramente relativista (o postnewtoniana) debida a la curvatura del espacio inducida por la presencia del Sol. Einstein insistió entonces en la posibilidad de edificar su teoría en un próximo eclipse solar. Europa se encontraba en guerra y no fue posible llevar adelante esta tarea pronto, pero aun así la Real Sociedad Astronómica de Londres organizó un par de expediciones para aprovechar el eclipse solar del 29 de mayo de 1919. Una expedición fue dirigida por el físico y astrónomo inglés Arthur Eddington (1882-1944) y trabajó en la Isla Príncipe en el Golfo de Guinea, mientras que la otra, dirigida por el astrónomo Andrew Crommelin, operó en Sobral, Brasil. Se tomaron fotografías de las estrellas en la región ocupada por el Sol durante el eclipse y varios meses antes; la comparación entre ellas mostró una desviación de las estrellas brillantes cercanas al Sol, igual a la predicha por Einstein. 7
En noviembre de 1919 la prensa de todo el mundo publicó la noticia. Einstein se transformó de la noche a la mañana en un segundo Newton, o más aún, en el científico que superó a Newton, y fue consagrado por la prensa y la opinión pública como el científico más popular de todos los tiempos. Aunque no sin emoción, cuando Einstein supo por un telegrama de Lorentz que los resultados de las expediciones iban por buen camino, su primera reacción fue comunicarlo a su madre mediante una tarjeta postal. Desafortunadamente, la madre no logró gozar mucho tiempo del triunfo inmenso de su hijo, pues murió en marzo de 1920, precisamente en casa de él, a donde, ya muy enferma, se trasladó para morir a su lado.
La enorme popularidad que alcanzó Einstein, combinada con su abierta vocación antimilitarista y pacifista y su defensa de los derechos judíos, despertó reacciones muy variadas. 8 Trágicamente, una de las más inmediatas fue la de hostilidad en base al antisemitismo que el ambiente político de la Alemania de 1920 ya alimentaba. En febrero de este año, durante una conferencia de Einstein en la Universidad de Berlín, se desataron violentos desórdenes de origen antisemita, y en agosto del mismo año se organizó un mitin en la más grande sala de conciertos de la ciudad para atacar la teoría de la relatividad, por tratarse de ciencia judía. Este tipo de manifestaciones y persecuciones se continuaron y profundizaron durante el ascenso del nazismo, y son las que obligaron finalmente a Einstein a abandonar la Alemania nazi en 1933, pese a su promesa a Planck de no dejar Berlín mientras fuera posible resistir.
Para colaborar a la recolección de fondos para la construcción de la Universidad Hebrea de Jerusalén, Einstein viaja junto con Chaim Weizmann (1874-1952) —fundador del Estado de Israel y su primer presidente— a los Estados Unidos de abril a mayo de 1921. Éste fue su primer viaje a ese país y lo aprovechó al máximo para realizar actividades científicas. Un año después acepta figurar como miembro del Comité de Cooperación Intelectual de la Sociedad de Naciones —el organismo internacional que en aquella época desempeñaba el papel que hoy corresponde a las Naciones Unidas— y, a pesar de que Alemania no era miembro de la Sociedad, conservaría su cargo hasta 1932. En junio de 1922 es asesinado su amigo, el Ministro de Asuntos Exteriores, 9 como resultado del clima de violencia que se extiende en Alemania.
Einstein entiende que su vida esta en peligro y decide alejarse un tiempo; hace un largo viaje por el Oriente, incluyendo Japón (octubre de 1922 febrero de 1923). Durante el recorrido se le informa que se le ha otorgado el premio Nobel de física (correspondiente a 1921) "por sus servicios a la física teórica y especialmente por su descubrimiento de la ley del efecto fotoeléctrico": ni la teoría de los fotones ni la relatividad fueron razones suficientes, aun en 1922, para otorgarle el premio Nobel. Pero cuando Einstein dio su conferencia Nobel en Goteburgo, Suecia, en julio de 1923 —precisamente en los días en que Compton mostraba en forma definitiva la validez de la teoría de los fotones propuesta desde 1905—, seleccionó la teoría general de la relatividad como tema. Es interesante señalar que el dinero del premio ya Einstein lo tenía comprometido (desde 1919 cuando se divorciaron) con Mileva Maric para la atención de los hijos. En 1925 Einstein hace otro largo viaje, esta vez por América del Sur.
Durante estos años se ha ocupado de la teoría cuántica y ha empezado a investigar en una nueva dirección, más ambiciosa aún que la relatividad: la teoría unificada de campo; ya tendremos oportunidad más adelante de hablar algo sobre estos temas. Asimismo, Einstein realizó en esta época una serie de trabajos experimentales y obtuvo un número considerable de patentes, especialmente en colaboración con el físico y biofísico húngaro Leo Szilard, (l898-l964) —a quien reencontraremos más adelante desempeñado un papel muy interesante en la vida de Einstein—. Incluso se ocupó de desarrollar un amplificador acústico para ayudar a una amiga cantante que estaba perdiendo el oído.
NOTAS
1 Se trata del electrómetro propuesto en el artículo número 23 citado en el Apéndice I, que no pudo desarrollar en Berna por falta de condiciones.
2 La dirección del Instituto era una tarea relativamente simple, pues en sus años iniciales —los que le corresponderían a Einstein— tendría como tarea básica otorgar becas de estudio.
3 Se recuerda al lector que el número p =3.14159... es definido precisamente como el conciente entre la circunferencia y su diámetro. La geometría usual (llamada euclideana por su primer expositor sistemático, el matemático griego Euclides) demuestra que esta razón es la misma para todos los círculos, y es costumbre universal llamarle a esta constante con la letra griega pi.
4 Un teorema es una verdad que se demuestra mediante argumentos lógicos a partir de los axiomas. Los axiomas son verdades que se aceptan a priori, es decir, son los postulados.
5 Recientemente (1971) se realizó otro tipo de experimentos para observar la dilatación relativista y gravitacional del tiempo. comparando la marcha de dos relojes atómicos iguales, uno en reposo en la Tierra y el otro circunvolándola a 10 000 m de altura, transportado en un jet comercial. Los resultados experimentales coinciden excelentemente con las predicciones de la teoría, tanto para vuelos E-W como W-E.
6 Este fenómeno se conoce con el nombre de corrimieno del perihelo. El perihelio es el punto de la órbita de un planeta más próximo al Sol. El fenómeno es sumamente pequeño — 43 segundos de arco en un siglo para Mercurio, que es el caso más notable— pero medible porque sus efectos se acumulan con el tiempo.
7 La predicción de Einstein era que las estrellas deben desviarse un ángulo de 1.75 segundos de arco; la desviación puramente newtoniana es igual a O.85". Las mediciones en Sobral dieron el resultado 1.98 ±;1; O.12",.mientras que las de Isla de Príncipe arrojaron el valor 1.61 ± 0.3". Tres años después observaciones de otro eclipse desde Australia dieron el resultado 1.72± 0.11".
8 Einstien recalcó en un artículo suyo publicado en el Times de Londres el 28 de noviemmbre de 1919 la importancia moral y política que tenía el hecho de que científicos ingleses hubieran realizado el esfuerzo de comprobar la teoría de un físico alemán, cuando sus respectivos países se encontraban en guerra.
9 Se trata de Walther Rathenau. Einstein le había aconsejado que no aceptara el puesto de Ministro, pues "los judíos peligran en posiciones tan altas."