VI. SISMICIDAD Y RIESGO S�SMICO
VARIAS NACIONES se encuentran dispuestas a gastar fuertes sumas en mantener redes s�smicas extensas, densas y complejas para poder observar, localizar, caracterizar y dar informes sobre la mayor cantidad posible de sismos. �Por qu�? Una muy buena raz�n es que conocer la sismicidad (i. e., la ocurrencia y distribuci�n de los sismos) permite, adem�s de estudiar los procesos tect�nicos, evaluar probabilidades para la ocurrencia de sismos. En este aspecto de la sismolog�a, la correcta aplicaci�n de t�cnicas estad�sticas sirve, no s�lo para determinar modelos apropiados a los datos, que permitan el c�lculo de probabilidades, sino adem�s para evaluar la aplicabilidad de los modelos empleados y la confiabilidad de las probabilidades calculadas y de los mismos datos.
Una recopilaci�n de datos acerca de los sismos que incluya tiempo y fecha de ocurrencia, localizaci�n (epi o hipocentro, regi�n donde ocurri�), tama�o (magnitudes y/o intensidades), descripci�n m�s o menos somera de los da�os causados, tiempos de arribo a las estaciones observadas, y algunos otros datos pertinentes, es llamada cat�logo. Actualmente casi todos los observatorios o redes sismol�gicas publican cat�logos; y existen tambi�n cat�logos, algunos muy antiguos, que contienen datos (recopilados a veces a partir de otros cat�logos) de regiones determinadas. Como la sismolog�a es una ciencia relativamente nueva, la mayor parte de los cat�logos, llamados instrumentales porque est�n basados principalmente en observaciones de sism�grafos, no se remontan m�s que a algunas decenas de a�os. Sin embargo, existen cat�logos descriptivos muy antiguos; en China se tiene una historia s�smica que comienza en el siglo XII a.C. (1), y algunos cat�logos japoneses se remontan hasta el a�o 599 de nuestra era (2).
Un problema grave de los cat�logos antiguos consiste en que es necesario corregirlos, debido a varios factores: poblaci�n de la �poca, exageraciones, errores de transcripci�n (rara vez se encuentra la versi�n original), p�rdida de partes, cambios en las regiones muestreadas, etc. (1). Sin embargo, la aplicaci�n de t�cnicas estad�sticas muy refinadas permite aprovechar gran parte de la informaci�n antigua (3).
En M�xico tenemos muy pocos datos acerca de los sismos que ocurrieron antes de 1910, cuando se fund� el Servicio Sismol�gico Nacional. Relaciones en documentos antiguos y en las Cr�nicas de Indias permiten conocer algunos datos de sismos que se remontan hasta el siglo XV, y hay datos y boletines s�smicos editados por los operadores de la red de tel�grafos a finales del siglo pasado (4). Posiblemente estudios antropol�gicos y arqueol�gicos, as� como paleogeol�gicos, permitan extender al pasado un poco m�s los cat�logos.
El af�n de tener cat�logos lo m�s extensos posible va m�s all� de la mera curiosidad
cient�fica; los grandes terremotos (
),
que son los que encierran m�s inter�s, tienen tiempos de recurrencia del orden
de varias d�cadas: 27 a 117 a�os en el caso de sismos 
en las m�rgenes de subducci�n del Pac�fico (5), y de 33 � 8 a�os, para los 
en
la trinchera mesoamericana (6), de manera que es imposible determinar si existen
periodicidades en su ocurrencia y cu�les son sus variaciones si no podemos estudiar
varios ciclos completos.
VI. 1.1 Estad�stica global. Los primeros estudios estad�sticos de sismicidad fueron hechos por Gutenberg y Richter en 1954 (7). Ambos estudiaron los datos disponibles de todas las regiones de la Tierra y encontraron que el n�mero N de sismos mayores de una magnitud M, que ocurren en un tiempo determinado, es funci�n de la magnitud:
donde a es una constante que depende del tiempo de muestreo y b tiene valores caracter�sticos para distintas regiones de la Tierra. Esta f�rmula, conocida como "Relaci�n de Gutenberg-Richter" o "Relaci�n G-R", nos dice que, si en un tiempo determinado ocurren, digamos, 10 000 sismos de magnitud 3, en el mismo tiempo ocurrir�n 900 de magnitud 4 y 81 de magnitud 5, de manera que la raz�n del n�mero de sismos de cualquier magnitud, entre el de la magnitud inmediata, siempre ser� constante.
Si hacemos una gr�fica del logaritmo del n�mero de sismos contra la magnitud,
la relaci�n de Gutenberg y Richter es una recta como la que se muestra en la
figura 42. Sin embargo, vemos en ella que los puntos que representan las observaciones
no se ajustan a �sta en el caso de magnitudes muy peque�as o muy grandes. Este
fen�meno puede deberse, al menos parcialmente, a fallas en el muestreo: los
sismos muy peque�os no se alcanzan a registrar en un n�mero suficiente de estaciones,
y por lo tanto no son localizados ni reportados; mientras que los sismos muy
grandes ocurren tan raramente, que los tiempos de muestreo no son significativos,
y si se hubiera muestreado un tiempo mucho m�s largo, los datos referidos a
las grandes magnitudes s� se ajustar�an a la recta. Aparentemente la explicaci�n
acerca de los sismos peque�os es correcta; pero parece que, adem�s del efecto
de tiempos de muestreo cortos, y corrigiendo el posible efecto de saturaci�n
de las magnitudes, existe un tope superior para el tama�o de los sismos, debido
a la cantidad de esfuerzo que puede soportar el material terrestre y a las dimensiones
propias de los continentes (8).
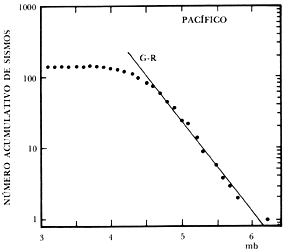
Figura 42. N�mero acumulativo de sismos para toda la regi�n del Pac�fico. La l�nea recta representa la relaci�n G-R.
Otras caracter�sticas importantes, de tipo estad�stico, de la sismicidad global son las siguientes: la probabilidad de ocurrencia de un sismo de una magnitud dada es constante en el tiempo, es decir, no depende de que acaben de producirse grandes sismos, o de que haga mucho que no ocurran; los intervalos peque�os entre los sismos son m�s probables que los largos; la probabilidad de que se den en forma simult�nea es muy peque�a. La distribuci�n estad�stica (esto es, el porcentaje de veces que ocurre cada uno de los posibles resultados de un proceso, cuando se ha observado un n�mero muy grande de realizaciones del mismo) que corresponde a estas caracter�sticas se llama distribuci�n de Poisson (9).
VI.1.2 Estad�sticas regional y local. Sin embargo, sabemos que la probabilidad de ocurrencia de un sismo no es igual en todas las regiones de la Tierra; existen zonas donde ocurren much�simos sismos y otras as�smicas. La probabilidad de ocurrencia de un sismo en M�xico es mayor que la de uno en Australia, por ejemplo. La relaci�n n�mero de sismos contra magnitud es distinta de una regi�n a otra. Aunque en muchas de ellas se considera que puede ser adecuadamente representada por una relaci�n como la global, aparentemente en otras, como M�xico, la relaci�n presenta magnitudes "favoritas", esto es, que son m�s frecuentes de lo que predice una relacion como la global, y que aparecen en la figura 43, que representa la sismicidad en M�xico, como un "chipote" por encima de la recta de Gutenberg y Richter (10).
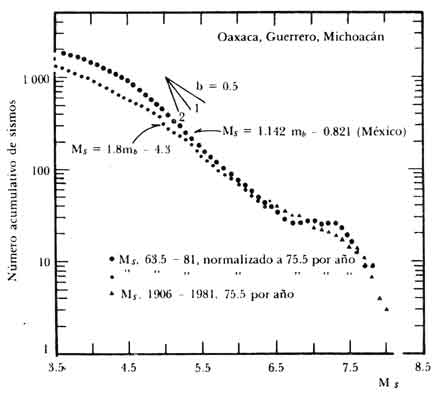
Figura 43. N�mero acumulativo de sismos para la regi�n de la Trinchera Mesoamericana
que comprende Oaxaca, Guerrero y Michoac�n. N�tese el "chipote" en las magnitudes
de 7.0 a 7.4.
Si ahora, en vez de estudiar una regi�n tan grande como un pa�s completo nos fijamos en una zona determinada, digamos Michoac�n, vemos que ya no se aplican las observaciones estad�sticas globales o regionales. La ocurrencia de un sismo grande en un lugar s� cambia las probabilidades de ocurrencia de otros sismos; un caso claro es el de la ocurrencia de r�plicas, que son indefectiblemente observadas tras un sismo grande. Para un punto particular, sobre todo si se encuentra cercano a una falla o zona s�smica activa, no es apropiado un modelo estad�stico como el de Poisson; el proceso que adoptemos para modelar la sismicidad del lugar debe "tener memoria", i. e., ser causal (depender de lo que haya pasado antes) (11 y 12). La estad�stica nos dice que la suma de muchos procesos causales se comporta como un sistema de Poisson (2); es por esto que la distribuci�n de la sismicidad global de la Tierra, la suma de todas las zonas s�smicas, es la de Poisson (1).
Si pudi�ramos conocer cada uno de los factores que influyen en la sismicidad y describir cada punto del terreno, cada ruptura, cada roca, etc., entonces podr�amos describir de manera anal�tica el proceso s�smico y predecir la ocurrencia de los terremotos como la de los eclipses. Desgraciadamente el n�mero de par�metros es tan enorme que no podemos llegar a una descripci�n exacta; sin embargo, podemos aprovechar las propiedades estad�sticas para evaluar probabilidades, aun en el caso de sistemas peque�os como una zona s�smica particular. Aqu� el problema es de nuevo el de la falta de datos, pues si bien los cat�logos de la sismicidad de todo el pa�s contienen un n�mero grande de datos, los referentes a una zona en particular son pocos. Es necesario instrumentar adecuadamente las zonas s�smicas de M�xico (y del mundo) para poder contar con un n�mero mayor de observaciones que permitan obtener resultados estad�sticamente confiables.
VI.1.3 Peligro potencial s�smico. �ste referido a un lugar determinado de la Tierra, es la probabilidad de que, en alg�n lugar de su entorno y dentro de un intervalo de tiempo determinado, ocurra un sismo que produzca un efecto determinado en ese lugar (com�nmente, una aceleraci�n dada). Usualmente no se toman en cuenta, para el c�lculo del peligro potencial s�smico, los posibles efectos de amplificaci�n local, directividad, etc., que puedan modificar los efectos esperados en un terreno est�ndar.
As�, el peligro potencial s�smico ser� muy grande en un lugar rodeado de fallas activas, o muy cercano a ellas (como, por ejemplo, Yakutat, en Alaska) y muy peque�o en los lugares lejanos de regiones sismog�nicas, independientemente de que �stos se hallen habitados o no.
Son claves esenciales para la evaluaci�n del peligro potencial s�smico la correcta evaluaci�n de la probabilidad de ocurrencia de sismos [la probabilidad de ocurrencia de un sismo de determinada magnitud, en un tiempo dado, se llama riesgo de sismo (2); y es distinto del riesgo s�smico definido m�s adelante] en las posibles fuentes situadas alrededor de un lugar determinado; lo cual requiere, naturalmente, poderlas identificar como tales. Aqu�, de nuevo, son de gran utilidad otras ciencias afines a la sismolog�a, como la geolog�a (13 y 14), los m�todos el�ctricos (resistividad, magnetismo, gravimetr�a, etc.) que permitan localizar posibles fallas sismog�nicas. De nuevo resulta esencial contar con cat�logos que permitan evaluar las probabilidades, y que sean aplicables varios de los m�todos usados para la predicci�n que ser�n discutidos m�s adelante.
Se llama riesgo s�smico a la probabilidad de ocurrencia, dentro de un plazo dado, de un sismo que cause, en un lugar determinado, cierto efecto definido como p�rdidas o da�os determinados.
En el riesgo influyen el peligro potencial s�smico, los posibles efectos locales de amplificaci�n, directividad, etc., la vulnerabilidad de las construcciones (e instituciones) y las p�rdidas posibles (en vidas y bienes) (15).
El riesgo s�smico depende fuertemente de la cantidad y tipo de asentamientos humanos localizados en el lugar. Aunque el peligro potencial s�smico es muy alto en Yakutat, el riesgo s�smico es peque�o porque es una regi�n con relativamente pocos habitantes; por otro lado, el potencial s�smico no es tan grande en Managua (porque all� los sismos no son tan grandes) pero la cantidad de personas que viven all�, la cercan�a a las fallas (16), y el tipo de construcci�n, hacen que el riesgo s�smico sea muy grande; esto es claro al comparar el n�mero de v�ctimas, para uno y otro lugar, mostrados en la introducci�n.
El riesgo s�smico en la ciudad de M�xico var�a much�simo de lugar a lugar; es grande en la zona centro, construida sobre sedimentos lacustres, donde el efecto local de amplificaci�n de ondas de periodos del orden de 2s, derrib� gran cantidad de construcciones durante el sismo del 19 de septiembre de 1985, y es peque�a en zonas como el Pedregal de San �ngel, donde las construcciones, de buena calidad generalmente, est�n asentadas sobre roca o sedimentos muy bien compactados (17). Sin embargo, el peligro potencial s�smico de esta ciudad no es muy grande, ya que se encuentra alejada de las regiones donde se producen los grandes terremotos.
VI.2.1 Efectos locales. Hemos mencionado arriba la influencia de efectos locales; ahora veremos, someramente, en qu� consisten. El efecto local m�s com�n es el de amplificaci�n de las ondas s�smicas; cuando una onda s�smica pasa de un medio a otro con diferentes propiedades el�sticas, su energ�a se divide, en general, en ondas transmitidas y reflejadas, cuya amplitud depende del �ngulo con el cual lleg� la onda incidente y de la diferencia entre las propiedades el�sticas de los medios. Si una onda pasa de cierto medio a otro con menor rigidez, podr� producir, con la misma energ�a, ondas de mayor amplitud, pues cuesta menos trabajo deformar el nuevo medio; esto es lo que pasa cuando una onda pasa de roca s�lida a sedimentos poco consolidados (18 y 19).
Otro efecto observado en sedimentos del tipo de arenas o arcillas es el de licuefacci�n, que hace que el terreno fluya como si fuera un l�quido (20). Esto es obviamente fatal para las construcciones asentadas sobre este tipo de suelos.
La forma del basamento en los valles puede hacer efecto de lente, enfocando las ondas s�smicas en determinados puntos o l�neas llamados c�usticas, a donde llegar�, por lo tanto, gran cantidad de energ�a, y pueden presentarse otros efectos de amplificaci�n debidos a la topograf�a o a una composici�n compleja del suelo (21 y 22).
Finalmente en lugares donde hay sedimentos confinados, como en los valles,
si la alimentaci�n de energ�a s�smica se prolonga durante un tiempo largo (del
orden de minutos), con ondas de periodo cercano al de los modos propios de los
sedimentos, �stos pueden comenzar a resonar, es decir, vibrar en sus
modos propios, de manera que el movimiento aumenta cada vez m�s, como un columpio
al que empujamos siguiendo el ritmo de sus oscilaciones (23). �ste es uno de
los efectos que causaron grandes da�os en la ciudad de M�xico en septiembre
de 1985. El efecto de resonancia a 2s es claro en los acelerogramas obtenidos
por el Instituto de Ingenier�a de la UNAM, en diferentes partes
del valle de M�xico; la figura 44 muestra un aspecto de las aceleraciones registrado
en la Ciudad Universitaria (a), fuera de la zona de da�os, y el obtenido en
el edificio de SCT (b) que result� da�ado por el sismo (24).
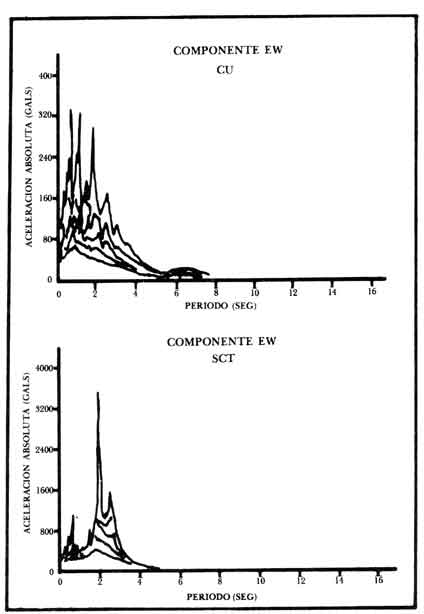
Figura 44. Espectros de la aceleracion en dos sitios del valle de M�xico.
Para el c�lculo del riesgo es necesario tomar en cuenta no s�lo el tama�o de los posibles sismos, sino tambi�n sus posibles funciones de fuente, pues los efectos sobre los edificios pueden variar dependiendo de la duraci�n y del contenido de frecuencias de las ondas (25); �sta es una de las causas por la que otros sismos grandes no han sido tan destructivos para los edificios de la ciudad de M�xico.
El c�lculo del riesgo s�smico es un factor importante para la planeaci�n de construcciones, especialmente hospitales, escuelas, plantas nucleares, etc., situadas en regiones s�smicas. Aunque es posible construir edificios que resistan cualquier tipo de sismo, generalmente no es costeable hacerlo, particularmente en pa�ses subdesarrollados. Los planeadores se encuentran ante disyuntivas como la siguiente: �qu� es mejor, construir 10 escuelas para las cuales el riesgo de que ocurra un sismo que alcance la aceleraci�n de dise�o durante los pr�ximos 10 a�os sea de 0.1%, o una sola escuela para la cual el riesgo sea de 0.001 %? �Es mejor permanecer inculto que exponerse al riesgo de 0.1%? �Si no se va a la escuela, est� uno a salvo del riesgo?
Obviamente es imposible evitar todo riesgo, pero generalmente es posible adoptar uno razonable (26) a cambio de gozar los beneficios de contar con escuelas, hospitales y otras construcciones que reportan beneficios al individuo y a la sociedad.
VI.2.2 Zonificaci�n. Determinar en un pa�s o una regi�n las zonas de alto y bajo riesgo s�smico seg�n las condiciones locales (cercan�a a fallas activas, peligro s�smico en ellas, efectos de la estructura local del suelo, etc.) que afectar�an a una construcci�n tipo (lo que permite definir el riesgo a partir de una aceleraci�n, en general horizontal, llamada aceleraci�n de dise�o), se llama zonificaci�n (27), y es de gran utilidad para la elaboraci�n y aplicaci�n de c�digos de construcci�n.
Cuando la zonificaci�n se hace con gran detalle, como el necesario para describir el riesgo s�smico de las distintas partes de la ciudad de M�xico, se llama microzonificaci�n.
Generalmente los valores de peligro potencial y riesgo s�smicos, reflejados en la zonificaci�n, se consideran invariantes en el tiempo; por lo que son apropiados como base para tomar medidas preventivas permanentes, como c�digos de construcci�n (28).
1. Lee, W., y D. Brillinger (1979), "On Chinese earthquake history An attempt to model an incomplete data set by point process analysis". Pageoph, vol. 117, pp. 1229-1257.
2. Lomnitz, C. (1974), Global Tectonics and Earthquake Risk. Elsevier Publish. Co.
3. Kijko, A., y M. Sellevol (1986), "Bayesian estimation of seismic parameters for extreme historical and incomplete instrumental data". Seismological Observatory, University of Bergen, Norway, Seismo-series n�m. 7.
4. Esp�ndola, J., y Z. Jim�nez (1984), Terremotos y ondas s�smicas,
Cuadernos del Inst. Geofís. / 1, UNAM, M�xico.
5. Rikitake, T. (1976), "Recurrence of great earthquakes at subduction zones". Tectonophysics, vol. 35, pp. 355-362.
6. McNally, K. (1981), "Plate subduction and prediction of earthquakes along the Middle American Trench", en Earthquake Prediction - An international Review, Simpson, D., y P. Richards (comps.), Maurice Ewing Ser. 4, Amer. Geophys. Union, EUA, pp. 63-72.
7. Gutenberg B., y C. Richter (1954), Seismicity of the Earth and Associated Phenomena. Princeton Univ. Press.
8. Wyss, M. (1979), "Estimating maximum expectable magnitude of earthquakes from fault dimensions". Geology, vol. 7, pp. 336-340.
9. Gnedenko, B. (1969), The Theory of Probability. Mir Publ., URSS.
10. Singh, S., M. Rodr�guez y L. Esteva (1983), "Statistics of small eartquakes and frequency of occurrence of large earthquakes along the Mexican subduction zone". Bull. Seis. Soc. Amer., vol. 73, pp. 1779-1796.
11. Esteva, L. (1976), "Seismicity", en Seismic Risk and Engineering Decisions, C. Lomnitz y E. Rosenblueth (comps.), Elsevier Sc. Publ. Co., pp. 179-224.
12. Hagiwara, Y. (1974), "Probability of earthquake occurrence as obtained from a Weibull distribution analysis of crustal strain". Tectonophysics, vol. 23, pp. 313-318.
13. Allen, C. (1976), "Geological criteria for evaluating seismicity", en Seismic Risk and Engineering Decisions, C. Lomnitz y E. Rosenblueth (comps.), Elsevier Scientific Publish. Co., Pa�ses Bajos, pp. 31-69.
14. Sieh, K (1981), "A review of geological evidence for reccurrence times of large earthquakes", en Earthquake Prediction, Maurice Ewing Series 4, D. Simpson y P. Richards (comps.), Am. Geophys. Union, pp. 181-207.
15. Mayer-Rosa, D. (1986), Tremblements de terre. Origine, risque et aide.
Comisi�n Nacional Suiza de la UNESCO y Comisi�n Nacional Suiza
de Geofísica.
16. Langer, C., M. Hopper, S. Algermissen y J. Dewey (1974), "Aftershocks of the Managua, Nicaragua, earthquake of December 23, 1972". Bull. Seism. Soc. Amer., vol. 64, pp. 1005-1016.
17. II, UNAM (1985), El temblor del 19 de septiembre de 1985 y sus efectos en las construcciones de la ciudad de M�xico. Informe preliminar, Instituto de Ingenier�a, UNAM, M�xico.
18. Kovacs, W., y J. Yao (1972), "Microzonation in design of seismic structures", en Proceeds. Int. Conf. Microzonation, Seattle, EUA, oct.-nov. 1972, pp. 665-670.
19. Tucker, B., y J. King (1984), "Dependence of sedimentfilled valley response on input amplitude and valley properties". Bull. Seism. Soc. Amer., vol. 74, pp. 153-165.
20. Faccioli, E., y D. Res�ndiz (1976), "Soil dynamics: behaviour including liquefaction", en Seismic Risk and Engineering Decisions, C. Lomnitz y E. Rosenblueth (comps.), Elsevier Scientific Publish. Co., Pa�ses Ba os, pp. 71-139.
21. Brune, J. (1976), "The physics of earthquake strong motion, en Seismic Risk and Engineering Decisions, C. Lomnitz y E. Rosenblueth (comps.), Elsevier Scientific. Publ. Co., Pa�ses Bajos, pp. 141-177.
22. Mungu�a, L., y J. Brune (1984), "Local magnitude and sediment amplification observations from earthquakes in Northern Baja California-Southern California region". Bull. Seism. Soc. Amer., vol. 74, pp. 107-119.
23. Bard, P., y M. Bouchon (1985), "The two dimensional resonance of sediment filled valleys". Bull. Seism. Soc. Amer., vol. 75, pp. 519-541.
24. Prince, J., R. Quaas, E. Mena, L. Alc�ntara, D. Almora, A. Barreto, C. Carmona, R. Carrera, G. Ch�vez, R. Delgado, S. Medina, M. O�ate, P. P�rez, M. Torres, R. V�squez yJ. Velasco (1985), Espectros de las componentes horizontales registradas por los aceler�grafos digitales de M�xico D. F. Sismo del 19 de septiembre de 1985. Instituto de Ingenier�a, UNAM, Informe IPS-10D.
25. Hall, J., y J. Beck (1986), "Structural damage in Mexico City". Geoph. Res. Lett., vol. 13, pp. 589-592.
26. Foster, H. (1980), Disaster Planning. Springer-Verlag, EUA.
27. Gaus, M., y M. Sherif (1972), "Zonation and microzonation", en Proceeds. Int. Conf. Microzonation, Seattle, EUA, oct.-nov. 1972, pp. 3-11.
28. Evison, E (1982), "Earthquake forecasting and countermeasures planning". Earthquake. Pred. Res., vol. 1, pp. 115-124.
