VII. FENÓMENOS FUERA DE EQUILIBRIO
AL PRINCIPIAR el capítulo IV hicimos notar que con el modelo cinético
un tanto rudimentario que implementamos en el capítulo III podíamos extraer
cierta información acerca de los fenómenos que ocurren en la materia cuando
ésta se encuentra en equilibrio o fuera de él. Los fenómenos tratados en los
capítulos V y VI se clasificarán bajo el primer rubro, esto es, fenómenos que
pertenecen al dominio del equilibrio. ¿Pero es esto realmente cierto? Cuando
pensamos en la evaporación de un líquido, en la fusión de un sólido o en otros
cambios similares, no podemos más que recordar la frase cotidiana: ¿cuánto tiempo
le tomará al agua en hervir? O bien, si hay un apagón, alguien dirá que "al
cabo de poco tiempo se descongelará el refrigerador". Entonces, ¿por qué hemos
insistido en incorporar a estas transformaciones bajo el rubro de fenómenos
de equilibrio? Esta es una pregunta justa y al mismo tiempo sutil. Si el lector
vuelve unas páginas hacia atrás y medita un poco sobre los argumentos utilizados
para visualizar los fenómenos descritos en términos de la dinámica molecular
subyacente a cada fase de la materia, notará que para nada hemos empleado el
factor "tiempo".
¿Concuerda esto con la realidad? ¿Es necesario hacerlo? En realidad, no lo es. Dentro del esquema de los fenómenos que podemos intentar comprender, con independencia del intervalo de tiempo que les tome en ocurrir, es correcto. Pero esto requiere ciertamente de un cierto grado de abstracción. Y lo que hemos hecho en dichos capítulos es precisamente eso. Hemos dado una interpretación de lo que ocurre a nivel molecular para diversos fenómenos, sin importar o tomar en cuenta el tiempo que tardan en ocurrir. Por ello dijimos que la teoría fenomenológica que aborda estas situaciones es la termostática. En ella sólo interesa describir lo que es inherente a dos estados de equilibrio: el final y el inicial. Si evaporamos un líquido, el estado inicial es el líquido en equilibrio y el estado final el gas en equilibrio. El proceso puede durar unos minutos o 100 años. La dinámica misma no concierne a la termostática. A ésta sólo compete escudriñar el sistema antes y después de la transformación y no lo que ocurre durante ella. Este problema es, por supuesto, mucho más complejo. Cuál es el papel que desempeña cada molécula, su interacción con las moléculas vecinas, la evolución de este complejo molecular desde que empieza como un líquido y termina como un gas, requiere de un examen mucho más detallado que el que hemos ofrecido en las páginas anteriores. Es claro que no pretendemos en este tratamiento introductorio ofrecer al lector un panorama completo sobre esta problemática. De hecho, aun a finales del siglo xx, muchas de estas cuestiones todavía no están completamente esclarecidas. De cualquier manera veamos qué podemos aprender con lo que ya sabemos sobre fenómenos dependientes del tiempo; sobre lo que de ahora en adelante clasificaremos como procesos irreversibles.
Para ello regresemos a nuestro modelo cinético y veamos cómo se comportarían las moléculas que forman el gas si las sometemos a una perturbación externa. Recordemos el contenido básico de una de las leyes de Newton: si un cuerpo dado no lo sometemos a la acción de una fuerza externa, o bien se mantendrá en reposo, o bien continuará moviéndose con velocidad constante. ¡Una lección que los automovilistas parecen no aprender cuando se les pide que mantengan una velocidad máxima en una carretera! El pie sobre el acelerador es la causa que produce la fuerza necesaria para acelerar al automóvil a velocidades mayores que la deseable. ¿Qué ocurre si en una forma menos imprudente y desde luego más iluminante perturbamos el estado de equilibrio del gas formado por las bolas de billar de nuestro modelo? Examinémoslo y aprendamos ciertamente más de lo que lo hace el imprudente automovilista. ¿Qué quiere decir en nuestro modelo "perturbar el gas de su estado de equilibrio"? El lector sagaz adivinará o intuirá que la respuesta está conectada en alguna forma con la modificación de la distribución de las velocidades de las moléculas del gas. Si la temperatura de éste se mantiene constante, la energía cinética promedio por molécula no varía con el tiempo, ya que es proporcional a la temperatura. Si ningún agente externo perturba de alguna manera las velocidades, éstas, que varían continuamente por las colisiones, mantendrán una distribución que, como ya dijimos, tampoco cambiará con el tiempo. Lo mismo ocurrirá si nada afecta al hecho de que el número de partículas por unidad de volumen sea el mismo, esto es, que se mantenga constante en el tiempo. Pues bien, estas características del comportamiento de las moléculas de un gas, representado por nuestro modelo, cuando aquél está en equilibrio, nos sugiere también la forma de alterar dicho estado de equilibrio. Claramente se desprende de esta discusión que, dependiendo de la forma en que vayamos a perturbar el gas, éste responderá de una manera diferente. Si a una piedra le damos un empujón suficientemente fuerte, se moverá o no en cierto grado dependiendo de su peso. Pero si le damos un martillazo, lo más probable es que la hagamos añicos. Si en lugar de una piedra repetimos el experimento con un trozo de hule, seguramente lo moveremos al empujarlo y lo deformaremos si le damos un martillazo, pero difícilmente lo romperemos en pedazos. Así, un sistema reacciona de diversas maneras dependiendo de cómo lo perturbemos. Regresemos ahora a nuestro gas representado por el modelo cinético simple del capítulo III y veamos cómo responde ante diferentes perturbaciones.
Para comprender mejor los fenómenos que deseamos estudiar; detengámonos un
momento y recapacitemos sobre un aspecto del gas cuando está en equilibrio.
Recordemos que el concepto de presión está asociado a la fuerza que transmiten
por unidad de superficie y unidad de tiempo los billones y billones de moléculas
que golpean dicha superficie. Asimismo hemos determinado interpretar la temperatura
del gas como una medida de la agitación molecular; entendiendo ésta como la
energía cinética promedio por molécula. Si en termostática caracterizamos a
un gas en equilibrio cuando, por ejemplo, su presión y temperatura son constantes,
¿cómo podemos visualizar esta característica en términos de las colisiones moleculares?
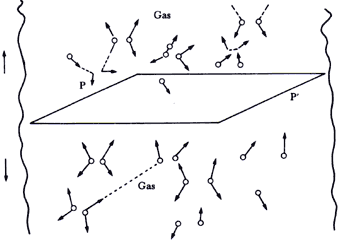
Figura 17 En equilibrio, el número de partículas que atraviesa un plano
P ubicado en cualquier sitio del recipiente que las contiene, es igual en las
dos direcciones señaladas hacia arriba  y hacia abajo
y hacia abajo ![]() respecto
a dicho plano. Como las moléculas "transfieren" ímpetu, energía cinética y masa
a través de dicho plano, esta transferencia es, en equilibrio, de igual magnitud
en ambas direcciones.
respecto
a dicho plano. Como las moléculas "transfieren" ímpetu, energía cinética y masa
a través de dicho plano, esta transferencia es, en equilibrio, de igual magnitud
en ambas direcciones.
La respuesta es muy simple. Imagine el lector que en cualquier sitio dentro
del recipiente que las contiene trazamos un plano, como el plano PP' de la figura
17, separando dos regiones del propio recipiente lejos de las paredes. Como
la presión y la temperatura son constantes, la transferencia de ímpetu y de
energía causada por las moléculas que pasan de arriba hacia abajo por PP' después
de su última colisión tiene que ser forzosamente igual a la transferencia de
esas mismas cantidades por las moléculas que pasan de abajo hacia arriba, de
lo contrario la presión no sería la misma, ni tampoco la temperatura! En otras
palabras, el transporte neto de masa, ímpetu y energía cinética en equilibrio
a través de un plano cualquiera en el gas es igual a cero. Vale la pena mencionar
que el transporte nulo de masa, ímpetu y energía es una propiedad inherente
a la distribución de velocidades de Maxwell que como vimos, caracteriza el estado
de equilibrio del gas. Con la imagen gráfica aquí vertida nos evitamos una demostración
matemática un tanto elaborada para convencernos de que éste es en efecto así.
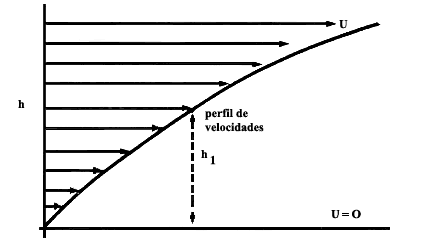
Figura 18. Un gas sometido a un perfil de velocidades, como el aquí mostrado, exhibe una resistencia entre capas adyacentes del gas a alturas diferentes. Esta resistencia o fricción interna da lugar al llamado coeficiente de viscosidad.
Cuando esta situación, a saber; el balance nulo de masa, ímpetu y energía que las moléculas, debido a las colisiones, transportan de una región a otra del recipiente se ve afectada por algún agente externo, el gas deja de exhibir sus propiedades de equilibrio. Como veremos a continuación, el transporte neto de masa de una región a otra del gas causado por ejemplo, por tener diferentes concentraciones de partícula, da lugar al conocido fenómeno de la difusión. Si por otra parte, modificamos en alguna forma el ímpetu de las moléculas en una región con respecto a los de otra, el transporte neto de éste provoca un fenómeno que se caracteriza por la viscosidad. Y finalmente, si alteramos la temperatura, esto es, la energía cinética promedio por molécula, ocurrirá, como el lector podrá sospechar, un mayor flujo de moléculas energéticas (mayor temperatura) a la región donde éstas tienen menor energía, es decir, habrá un flujo de calor. A estos fenómenos de fundamental importancia en todos los procesos donde ocurre un flujo de fluidos, sean líquidos o gases, se les conoce como fenómenos de transporte. Sobra decir que su conocimiento es vital en el problema de diseño de equipo, estudios de perfiles de flujo, estudios de procesos químicos, etc. Son la herramienta vital en muchos trabajos de ingeniería aeronáutica, química, mecánica, aeroespacial, industrial y otras. Analicemos uno por uno con más cuidado.
Tómese un vaso con agua limpia y colóquese en reposo sobre una superficie sólida, por ejemplo, una mesa. Teniendo mucho cuidado de no agitar el líquido, agregue una gota de tinta en un punto de la superficie del agua. En el transcurso del tiempo el punto azul donde se colocó la tinta se irá gradualmente dispersando por el agua dándole tintes azules a diferentes regiones del líquido. Si esperamos un tiempo suficientemente largo, de algunas horas probablemente, el agua aparecerá uniformemente coloreada. Este proceso que resulta de la interpenetración de las moléculas de tinta en el agua se conoce como difusión. Ejemplos típicos de este fenómeno los podemos observar en la vida cotidiana: el humo de un cigarrillo en un cuarto sin corriente de aire se dispersa lentamente en éste hasta que el color del humo se desvanece; si destapamos una botella de un gas oloroso como el amoniaco o el ácido sulfhídrico (olor característico de huevo podrido) en una esquina de una habitación, al cabo de unos minutos el olor se percibe en toda ella. Y existen muchísimos otros ejemplos de este proceso, no sólo entre gases, o gases y líquidos, sino también entre sólidos, o gases y sólidos. La difusión de gases en gases (de diferentes especies moleculares) fue estudiada exhaustivamente por el químico escocés Thomas Graham. En 1829 publicó una memoria sobre difusión gaseosa en la cual enunció su famosa ley:* "La rapidez de difusión de un gas en otro es inversamente proporcional a la raíz cuadrada de sus densidades". Esta relación fue cuidadosamente verificada por Graham midiendo experimentalmente la rapidez de difusión de varios gases como el hidrógeno (H2) el metano (CH4), el nitrógeno (N2), el bióxido de carbono (C02) y el oxígeno (02) en aire. Más tarde, en 1855, el químico alemán Adolfo Fick mostró que si la concentración de la sustancia que se difunde varía con la distancia en forma tal que el equilibrio del sistema no se perturbe fuertemente, el flujo de la sustancia que se difunde, la tinta en el ejemplo anterior; el amoniaco en el cuarto, etc., es proporcional a dicha variación en la concentración. Al coeficiente de proporcionalidad se le llama coeficiente de difusión.
Basándose en el modelo cinético que hemos empleado a lo largo de esta obra, esto es, el modelo cinético de un gas ideal, el físico alemán R. Clausius mostró en su famoso trabajo intitulado La naturaleza del movimiento que llamamos calor publicado en 1857 las implicaciones físicas del propio modelo. En particular hizo hincapié no sólo en la interpretación de la temperatura como una medida de la agitación molecular que ya discutimos ampliamente en el capítulo IV, sino también en las consecuencias de dicho resultado, a saber, que la raíz cuadrada del promedio del cuadrado de la velocidad es una medida de la velocidad que tienen las partículas a lo largo de la porción rectilínea de sus trayectorias entre dos colisiones sucesivas. De acuerdo con este resultado y si examinamos los números de la tabla 1, a un gas como el bióxido de carbono (C02) le tomaría fracciones de segundo difundirse en el aire, ya que sus moléculas viajan a más de 450 m/seg. Pero esto no es así. En 1858 el metereólogo holandés C.H.D. Buys-Ballot hizo ver que la difusión, aun de un gas en otro, es un proceso mucho más lento que lo insinuado por Clausius y que, en particular; el bióxido de carbono puede permanecer por un tiempo relativamente largo en un recipiente abierto al aire. La solución de esta paradoja fue dada parcialmente por el propio Clausius, quien intentó mostrar que en gases reales las moléculas no pueden viajar grandes distancias en líneas rectas debido a las fuerzas intermoleculares. Para ello introdujo uno de los conceptos más útiles en la teoría cinética moderna: el concepto de "trayectoria libre media". Esta trayectoria se define como la distancia máxima que en promedio una molécula puede recorrer entre dos colisiónes sucesivas. Grosso modo, entre mayor es la densidad de un gas, más probable que las colisiones sean más frecuentes y, por tanto, menor su trayectoria. Clausius logró mostrar que, en efecto, es inversamente proporcional a la densidad, pero esto no basta para satisfacer las objeciones de Buys-Ballot. La respuesta completa a este problema tuvo que esperar hasta un trabajo publicado en 1866 por otro gran físico, el escocés James Clerk Maxwell. Este trabajo es una versión corregida de una versión preliminar sobre cómo tratar los procesos de transporte con los métodos de la teoría cinética de Clausius. El trabajo inicial resultó ser incorrecto, como el propio Clausius se lo hizo ver. El resultado de Maxwell fue que el coeficiente de difusión es proporcional a la presión, lo cual concuerda satisfactoriamente con los experimentos realizados en gases a bajas densidades. Como dato interesante vale la pena hacer notar que este resultado obtenido por Maxwell para la difusión, así como los que discutiremos a continuación para la viscosidad y la conducción de calor; son, en orden de magnitud y en cuanto a su dependencia con la densidad y la temperatura, los mismos que se obtuvieron años más tarde por el propio Maxwell, Boltzmann, y ya en este siglo por Chapman y Enskog, usando métodos matemáticos sumamente refinados.
Por último, vale la pena mencionar que el resultado empírico sobre difusión gaseosa, obtenido por Graham y deducido más tarde por Clausius y Maxwell, desempeñó un papel muy importante en la separación del isótopo 235 del Uranio que es susceptible a la fisión nuclear y cuya abundancia es de 0.7%, del isótopo 238 del propio metal que no es fusionable, pero cuya abundancia es de 99.3%. El proceso de difusión se aplica no directamente al metal, sino a los compuestos gaseosos que forma con el flúor para dar los hexafluoruros U235 F6 y U238 F6.
Para comprender el concepto de viscosidad tomemos un libro grueso de pastas
blandas y coloquémoslo sobre una mesa. Fijemos la tapa del libro en contacto
con la superficie de la mesa deteniéndola con un dedo, y con la otra mano jalemos
la tapa superior en dirección paralela al plano de la mesa. Observaremos cómo
el desplazamiento de las hojas del libro en la dirección en que jalamos es cada
vez menor a medida que están más alejadas de la tapa. Al desliz de una hoja
dada que se le transmite por las hojas de arriba se opone la resistencia de
la hoja inmediatamente inferior a ella y las que le siguen. La fricción relativa
entre las hojas hace que el desplazamiento de ellas sea cada vez menor a medida
que nos alejamos del punto donde estamos jalando. En el caso de un fluido, esta
fuerza interna es la que se opone a que sea deformado cuando lo "jalamos". Sin
embargo, en este caso la deformación se logra aplicando una velocidad dada a
una capa superior del líquido y disminuyendo esa velocidad gradualmente hasta
mantener la capa inferior en reposo. La resistencia interna que opone el líquido
a la deformación se conoce como viscosidad. En la anterior figura 18 mostramos
este efecto gráficamente. Imaginemos un fluido, que puede ser un gas o un líquido,
confinado a un recipiente en el cual la capa superior la deslizamos con una
cierta velocidad, llamémosla u, de manera que dicha velocidad, como función
de la altura h, decrece paulatinamente hasta hacerse cero en la capa
inferior. Las capas vecinas de gas a diferentes alturas se deslizan una con
respecto a otra, como las páginas del libro, con diferentes velocidades. Así,
una capa de gas, digamos la que está a la altura h1 , jala
a la que está por debajo de ella y que se mueve con una velocidad menor. La
de arriba intenta mover más rápidamente a la de abajo, la cual se resiste a
ser arrastrada y trata de frenar a su vez a la de arriba. Esta fricción interna
es justamente lo que llamamos la viscosidad del gas. Desde el punto de vista
molecular; este fenómeno es muy fácil de explicar. Tomemos el plano de la figura
18 y coloquémoslo, mentalmente, en la posición h1 señalada.
Ahora las moléculas que pasan por dicho plano después de su última colisión
y que provienen de la parte superior tienen un ímpetu mayor que aquellas que
después de su última colisión pasan en dirección opuesta. La razón es claramente
que las de arriba tienen una velocidad mayor que las de abajo. El efecto que
esto tiene es el mismo que si arrojamos piedras de un furgón de ferrocarril
que se mueve con una velocidad mayor que otro, y de este segundo arrojamos piedras
de igual masa al primero. Las que provienen del furgón que se mueve más rápido
van a acelerar al furgón lento, en tanto que las que provienen de éste van a
decelerar al furgón rápido. En el caso de nuestro gas, el transporte neto de
ímpetu ocasionado por el paso de moléculas rápidas hacia abajo y lentas hacia
arriba produce una fuerza neta que es proporcional a la variación de la velocidad
con la altura h. Al coeficiente de proporcionalidad se le conoce como
coeficiente de viscosidad. En el caso de gases diluidos, Maxwell mostró, en
1866, usando los mismos métodos que empleó para la difusión que este coeficiente
es independiente de la densidad y proporcional a la raíz cuadrada de la temperatura.
Una vez más, para gases diluidos este resultado no sólo concuerda satisfactoriamente
con el experimento, sino que ha sido verificado en cuanto a su dependencia con
la temperatura por los métodos más sofisticados de la teoría cinética mencionados
en la sección anterior.
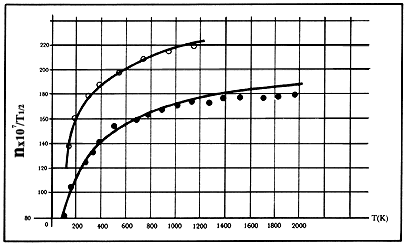
Figura 19. La viscosidad h para el neón
y el argón se exhiben como funciones de T. La ordenada es h
X 107 g-cm-1 seg-1 dividida por ![]() .
Los valores experimentales del neón están representados por círculos abiertos
O y los del argón por puntos negros. Las curvas sólidas están calculadas de
las fórmulas teóricas del formalismo de Boltzmann. La dependencia de
h en la temperatura como
.
Los valores experimentales del neón están representados por círculos abiertos
O y los del argón por puntos negros. Las curvas sólidas están calculadas de
las fórmulas teóricas del formalismo de Boltzmann. La dependencia de
h en la temperatura como ![]() es evidente.
es evidente.
En la figura 19 mostramos el coeficiente de viscosidad para el neón y el argón como función de la temperatura. En ella se muestra con toda claridad, aunque el cálculo está hecho con la teoría más sofisticada de Boltzmann, la dependencia de estos coeficientes de la temperatura.
Imaginemos ahora el mismo fluido que el considerado en la figura 17 excepto porque ahora las paredes superior e inferior se ponen en contacto con dos cuerpos a temperaturas diferentes. Supondremos que la pared superior está a una temperatura T2 mayor que la temperatura T1 de la pared inferior. Entre ambas paredes existirá pues una diferencia de temperaturas DT = T2 - T1, y claramente a cada altura h la temperatura será diferente. Las consecuencias de tener esta distribución de temperaturas la apreciará el lector de inmediato.
Hablando en un lenguaje cotidiano diremos que debido a la existencia de la
diferencia de temperatura DT
habrá un flujo de energía en forma de calor de la capa superior a la capa
inferior del fluido. Si consideramos este flujo por unidad de área y unidad
de tiempo, podemos describir, de acuerdo con la ecuación empírica descubierta
por J. Fourier en 1822 que ese flujo es proporcional a la diferencia de temperaturas
DT. Al coeficiente de
proporcionalidad se le conoce como la conductividad térmica del
material, en este caso del fluido. Pero también podemos dar una interpretación
molecular a este fenómeno si recurrimos a nuestro modelo cinético. En efecto,
volvamos a la figura 17 y examinemos ahora cómo se comportan las moléculas que
están arriba y por debajo de nuestro plano de referencia PP'. Como la temperatura
es mayor arriba de este plano, las moléculas que después de su última colisión
la atraviesan hacia abajo tienen mayor temperatura y por lo tanto su energía
cinética media es mayor que la de las partículas que después de su última colisión
pasan de abajo hacia arriba y que provienen de regiones más frías. Por lo tanto,
el balance neto de energía no es cero, sino la diferencia entre la energía cinética
que llevan las moléculas más calientes de arriba hacia abajo, menos la energía
cinética que llevan las moléculas más frías de abajo hacia arriba. Cuando se
hace el cálculo de este transporte neto de energía cinética que en nuestro modelo
ya hemos identificado como calor, se encuentra justamente la ecuación de Fourier.
La conductividad térmica del gas resulta ser como la viscosidad: independiente
de la densidad y proporcional a la raíz cuadrada de la temperatura. De nuevo
vale la pena mencionar que estas características de la conductividad térmica
se recuperan cuando se hace el tratamiento más sofisticado que ya mencionamos
en los dos casos anteriores. La comprobación de este resultado con el experimento
por lo general se lleva a cabo de una manera indirecta. Resulta que si se toman
las fórmulas para la viscosidad y la conductividad térmica calculadas por estos
métodos y se dividen entre sí, el cociente resultante es proporcional al calor
específico a volumen constante. Este calor específico que ya definimos en el
capítulo IV, es una cantidad fácilmente medible. Para el caso de moléculas esféricas,
como lo son el helio, el argón, el neón y el xenón, o sea los gases nobles,
el cociente entre la conductividad térmica y la viscosidad resulta ser; teóricamente,
igual a ![]() ,
,
La tabla II muestra la concordancia con el experimento en este caso y las discrepancias que aparecen cuando los gases ya tienen una estructura molecular más complicada.
TABLA II. El cociente entre la conductividad térmica y la viscosidad ( E ) llamado el parámetro de Eucken, se compara para varios gases:
|
|
||
|
Gas
|
e (observador)
|
e (teórico)
|
|
|
||
|
He
|
2.40
|
2.5
|
|
Ar
|
2.49
|
2.5
|
|
H2
|
1.965
|
1.93
|
|
N2
|
1.905
|
1.90
|
|
O2
|
1.913
|
1.90
|
|
CO
|
1.835
|
1.90
|
|
|
||
Antes de cerrar este capítulo es deseable insistir en la utilidad que representa
el tener métodos matemáticos basados en modelos moleculares para estudiar los
fenómenos de transporte. Y la forma más objetiva de hacer esto es mencionar
al lector por medio de un ejemplo explícito dónde aparecen estos coeficientes,
como son la viscosidad, la conductividad térmica y otros, en problemas prácticos.
En el flujo de fluidos compresibles a través de ductos, tales como tubos, canales
y otros, se presenta un problema en el cual la fricción interna (viscosidad)
siempre está acoplada con el problema del flujo de calor. Para determinar la
influencia de uno y otro en el flujo se usa un numero adimensional (¡entre muchos
otros!) llamado el número de Prandtl. Este número está definido como el cociente
entre el producto de Cp, el calor específico a presión
constante y la viscosidad h entre la conductividad térmica l:
El conocimiento de este número es de primordial importancia para innumerables problemas de ingeniería. Ahora bien, Cp se puede obtener de las propiedades de equilibrio del fluido, por lo que el disponer de métodos confiables para calcular ...h y l es más deseable. En la tabla III damos los valores de este número obtenidos con los valores de ... h y l para algunos gases calculados con el modelo cinético simple que hemos empleado. Si tomamos en cuenta las simplificaciones tan drásticas que se hicieron, la discrepancia entre los valores teóricos y experimentales no es tan mala, aunque a su vez es indicativa de lo importante que es mejorar la teoría.
TABLA III. Los valores teóricos para el número de Prandt calculados con el modelo cinético del gas ideal se comparan con los obtenidos experimentalmente para algunos gases monoatómicos y diatómicos. La discrepancia entre ambos refleja lo sobresimplificado del modelo teórico usado para describir el gas:.
|
|
||
|
Gas
|
Número de Prandtl calculado |
Observado
|
|
|
||
|
He
|
1.667
|
0.69
|
|
Ne
|
1.667
|
0.68
|
|
Ar
|
1.667
|
0.69
|
|
H2
|
1.40
|
0.71
|
|
N2
|
1.40
|
0.72
|
|
O2
|
1.40
|
0.71
|
|
|
||
NOTAS