VI. TEOR�A CIN�TICA DE LA MATERIA

COMO el lector habr� notado, en los cap�tulos anteriores se enfocaron a nociones b�sicas de la estructura molecular de la materia, empleando un modelo para un gas muy simple, pero poco realista. Como tambi�n vimos, este modelo resulta adecuado para describir las propiedades de los gases ideales. Estos gases, que no existen en la naturaleza, son imitados en cierta forma en su comportamiento por gases monat�micos de baja densidad, los que llamamos habitualmente gases diluidos. Sin embargo, en el mundo real, la materia dista mucho de comportarse as�. Como mencionamos al principio de este libro, la materia se nos presenta en fase gaseosa, l�quida o s�lida, y en cada una de estas fases tiene propiedades muy diferentes a las que exhibe en otras. Adem�s, tambi�n hemos insistido en que hay cambios de fase. En �stos las especies moleculares o at�micas que forman a la sustancia en cuesti�n se conservan inmutables, es decir; no hay reacciones qu�micas. De aqu� que algo debe pasar en ellas que altera de manera singular sus propiedades globales en la nueva fase. Ciertamente, todas estas peculiaridades est�n fuera del alcance del modelo empleado anteriormente. �Es entonces posible modificar dicho modelo para entender; por lo menos cualitativamente, cu�les son los mecanismos microsc�picos subyacentes a todas estas diferentes manifestaciones de la materia? La idea de este cap�tulo, y de ah� su t�tulo, es ilustrar al lector c�mo puede hacerse, en parte, tal modificaci�n y cu�les son las grandes dificultades que todav�a hoy en d�a mantienen en plena actividad a los f�sicos y qu�micos interesados en esta problem�tica.

FUERZAS INTERMOLECULARES

En el modelo cin�tico del gas ideal la �nica interacci�n entre esferas por las que consideramos est� formado el gas es causada por choques el�sticos. Esto es, las mol�culas no ejercen ninguna fuerza entre s�, ni con otras del sistema, excepto en el momento de la colisi�n.

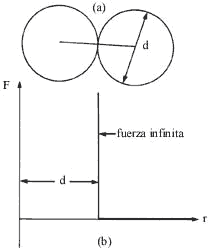
Figura 11. (a): Aqu� se muestra una colisi�n entre dos esferas impenetrables, cada una con di�metros d. (b): Si r es la distancia entre los centros de las esferas, la fuerza F graficada contra r es infinita si r es igual a d y cero para cualquier otro valor r mayor de d.

Ésta ocurre, como se muestra en la figura 11a, cuando la distancia entre los centros de las mol�culas es igual al di�metro de una de ellas. Como las esferas son, por hip�tesis, impenetrables, esta caracter�stica puede representarse por una fuerza que es infinita en el instante de dicha colisi�n e igual a cero para cualquier otra distancia de separaci�n entre ellas (Figura 11 b). En las mol�culas de los gases comunes y corrientes las cosas no ocurren as�. De hecho, las fuerzas intermoleculares son diferentes para distintas clases de gases. De esta forma, para los gases nobles y los vapores de algunos metales monat�micos, como el litio, el sodio, la plata, el mercurio y otros, las fuerzas entre los �tomos s�lo dependen de la magnitud de la distancia entre dos de ellos; esto es, la fuerza entre los �tomos s�lo act�a entre pares de ellos. Como los �tomos no tienen una estructura interna, pueden concebirse como esferas (no r�gidas), y como tales no exhiben diferentes configuraciones al variar su orientaci�n en el espacio. Por lo tanto decimos que las fuerzas son esf�ricamente sim�tricas. Si de nuevo llamamos d al di�metro de esas esferas, hay una fuerza repulsiva casi infinita cuando la distancia entre los centros de estos �tomos se aproxima al valor de un di�metro. A distancias cortas se comportan casi como esferas duras, pero a distancias mayores que d, las fuerzas entre ellas son atractivas. La magnitud de esta fuerza va siendo cada vez menor a medida que las mol�culas se alejan entre s�, para hacerse casi iguales a cero a distancias grandes. Usualmente estas distancias son del orden de una decena de di�metros moleculares (ver Figura 12).

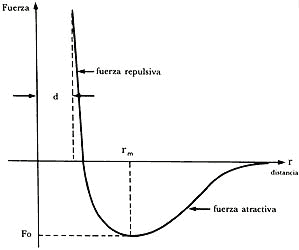
Figura 12. Dependencia de la fuerza con la distancia entre dos �tomos de un gas noble.

Para una cierta distancia r_m, la fuerza atractiva tiene en magnitud un valor m�ximo que representa la configuraci�n más estable que pueden formar dos �tomos. En t�rminos energ�ticos, se requiere de una cierta energ�a, por ejemplo, producida por la presencia de una tercera mol�cula energ�tica, para que los dos �tomos que originalmente se encuentran a la distancia r_m se alejen uno de otro.

Para gases formados por mol�culas m�s complicadas, como los gases diat�micos H₂, N₂ 0₂, CO, NO y otros, las fuerzas, aunque cualitativamente descriptibles, como en el ejemplo dado en la figura 12, pueden complicarse por la influencia de la estructura misma de la mol�cula. En gases poliat�micos como el agua (H₂, el amoniaco (NH₃, el metano (CH₄), etc., las complicaciones son cada vez mayores y, entre m�s compleja es la mol�cula, obviamente mayor es la complicaci�n.

Vamos a contentarnos en esta discusi�n con suponer que las fuerzas interat�micas o intermoleculares son de la forma general descrita en la figura 12. Es decir, entre N part�culas, sean �tomos o mol�culas, las part�culas interaccionan entre s� s�lo por pares. La interacci�n total es la suma de estas interacciones sobre todos los pares de mol�culas, las cuales son esf�ricamente sim�tricas. Aun con todas estas simplificaciones, la teor�a cin�tica resultante, que podr�a aplicarse a una variedad de sustancias en la naturaleza, introduce las suficientes complicaciones, cuyas consecuencias no han sido todav�a satisfactoriamente resueltas. Veamos cu�les son �stas antes de considerar mayores complicaciones.

GASES REALES

Imaginemos ahora un recipiente repleto de �tomos o mol�culas entre las cuales existe una interacci�n como la representada en la figura 12. �C�mo afecta esta modificaci�n en la fuerza interat�mica la dependencia de la presi�n con el volumen y la temperatura? �Y la dependencia de la energ�a interna con la temperatura? La respuesta a estas preguntas ya no es tan sencilla como las que pudimos dar en el caso del gas ideal. En la ecuaci�n de estado del gas ideal, la cual se obtiene sintetizando la Ley de Boyle y la Ley de Charles que vimos en el cap�tulo IV (v�ase Ap�ndice 2),

pV=uRT

el volumen V que aparece en el miembro izquierdo es el volumen total del recipiente que contiene a las part�culas. Esto implica que t�citamente hemos despreciado primeramente el volumen ocupado por las mol�culas. En efecto, si �stas son esferas de radio d/2, el volumen ocupado por cada una de ellas es de .

Si hay N mol�culas en el gas, ocupar�n un volumen de , y por lo tanto el volumen del espacio del contenedor accesible a ellas ser� de V - . A este volumen Clausius le llam� el covolumen, y propuso, en 1851, que la ecuaci�n de Boyle para el gas ideal se substituyera por:

p(V-b) = RT,

donde b = es el covolumen. Esta modificaci�n de la ecuaci�n de estado es acertada, pero no muy relevante. Un gas que obedece la ecuaci�n de Clausius no difiere mucho en sus propiedades de las de un gas ideal. Pero en 1872, el gran f�sico holand�s J. D. Van der Waals hizo ver que, debido a las fuerzas atractivas entre las part�culas, la presi�n efectiva sobre una superficie dada tendr�a que ser modificada. Una mol�cula que se acerca a una pared va a "pegarle menos fuerte" al verse sometida a la atracci�n de las mol�culas que la rodean. Por tanto, la fuerza del golpe es menor y eso redunda en una presi�n que tendr� que ser corregida por la presencia de estas fuerzas atractivas.

Rudolf Clausius

Razonando con respecto a estas ideas, Van der Waals logr� modificar la ecuaci�n de Clausius, sustituyendo el valor de la presi�n p por otro m�s complicado, que toma en cuenta la presencia de dichas fuerzas. La ecuaci�n resultante, ahora conocida con el nombre de la ecuaci�n Van der Waals, represent� el avance m�s notable en nuestro entendimiento del comportamiento de los gases reales alcanzado en el siglo XIX. Vale la pena insistir que de tal ecuaci�n es posible obtener una imagen cualitativa global de c�mo se comporta una sustancia pura, no s�lo en la fase gaseosa, sino tambi�n en la regi�n donde el gas coexiste en equilibrio con el l�quido —lo que comunmente llamamos ebullici�n— y en la regi�n donde la sustancia existe en forma de l�quido. Como vemos, �con una modificaci�n relativamente simple de nuestro modelo cin�tico podemos pasar, de la abstracci�n, a una situaci�n m�s apegada a la realidad! Los gases reales, como los conocemos en la vida cotidiana: el aire que respiramos, el vapor de una caldera, el anh�drido sulfuroso con que contaminamos el aire (S0₂), el amoniaco con que fabricamos fertilizantes, el bi�xido de carbono en que convertimos el ox�geno por el proceso de respiraci�n, etc., tienen propiedades todav�a m�s complicadas que las que pueden predecirse de un modelo cin�tico como el usado por Van der Waals. No obstante, este modelo ha servido para generar otros m�s complicados que permiten incorporar en su descripci�n a gases como los arriba mencionados. As� pues, la teor�a cin�tica nos permite establecer la plataforma m�nima del conocimiento a partir de la cual esas extrapolaciones tienen una base molecular.

LA FASE L�QUIDA

Todos sabemos diferenciar, en general, un l�quido de un gas. En el l�quido las mol�culas tienden a ocupar parcialmente el volumen del recipiente que las contiene, adquiriendo, en grueso, la forma geom�trica de �ste. Forma una superficie a lo largo de toda la porci�n en contacto con la atm�sfera que lo rodea, que es plana si la anchura del recipiente que lo contiene es grande, pero tambi�n sabemos que al ponerse en tubos peque�os forma una superficie curvada en general, llamada menisco. Adem�s, son mucho más dif�ciles de comprimir o de dilatar que los gases. Todo esto apunta a la posibilidad de que en el l�quido las mol�culas est�n m�s densamente empaquetadas entre s� que en el gas. En el lenguaje usado al estudiar el modelo cin�tico del gas ideal podr�a decirse que la "vida media" de las mol�culas, esto es, el tiempo entre dos colisiones sucesivas, debe ser muy peque�o comparado con el de un gas. Y ciertamente ya no podemos aceptar la tesis de las colisiones por contacto; si de acuerdo con la figura 11, s�lo hubiera fuerzas repulsivas en un l�quido, �ste seria "inestable". Estallar�a por la estrecha cercan�a que hay entre las mol�culas. Entonces, las fuerzas atractivas deben desempe�ar aqu� un papel preponderante. El vino de la pintura del gran Van Gogh, el vaso con agua que colocamos sobre la mesa..., son tan estables como una piedra, a menos que hagamos algo para perturbar esa estabilidad. �C�mo interpretar esta caracter�stica a nivel molecular?

En el caso de un gas, las mol�culas, aun considerando la presencia de fuerzas atractivas, pueden moverse libremente en todo el recipiente que lo contiene. La energ�a cin�tica promedio de una mol�cula, que hemos usado para interpretar a la temperatura a nivel molecular; llega a tener valores relativamente grandes. En un l�quido la situaci�n es parecida, excepto que debido a su mayor densidad, o sea al mayor n�mero de mol�culas por unidad de volumen, hace que la distancia intermolecular promedio sea mucho menor que para un gas. En consecuencia, una mol�cula, a pesar de chocar con sus vecinos un gran n�mero de veces, queda "enjaulada" por ellas, hasta que puede finalmente encontrar un hueco para escapar a otra regi�n, no menos densa que la anterior y de la cual tendr� tambi�n dificultades para salir (ver Figura 13). M�s que un movimiento �gil y vigoroso como lo visualizar�amos en un gas, una mol�cula de un l�quido camina a saltos de una regi�n a otra siguiendo un camino un tanto err�tico. Este movimiento es caracter�stico de los procesos difusivos, incluyendo en ellos al movimiento browniano.

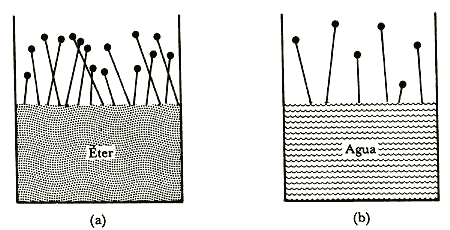
Figura 13. Evaporaci�n. (a) El �ter se evapora m�s f�cilmente que el agua, (b) porque las fuerzas atractivas entre sus m�leculas son m�s d�biles.

Con objeto de estudiar mejor y tener una idea m�s clara de lo que es un l�quido, se han hecho una multitud de experimentos conducentes a obtener informaci�n sobre c�mo est�n dispuestas las mol�culas en �l. Estos experimentos fueron iniciados por Max von Laue en 1912 en Alemania para averiguar la estructura de los s�lidos mediante la difracci�n de rayos X. Estos rayos, de muy peque�a longitud de onda, al incidir sobre el material son desviados de su trayectoria original por los �tomos que componen el s�lido. Los rayos desviados, al salir del s�lido, se registran en una placa fotogr�fica. Al revelar dicha placa se encuentra que alrededor de una intensa mancha negra central, que corresponde al rayo no desviado, hay un patr�n de manchas m�s d�biles dispuestas en un arreglo geom�trico. De aqu� pudo inferir Von Laue que los �tomos en un cristal est�n dispuestos de tal manera que forman un patr�n ordenado con geometr�as bien definidas. Al radiografiar a un l�quido se obtienen resultados sorprendentes. En efecto, si fijamos nuestra atenci�n sobre una part�cula arbitrariamente escogida del l�quido, se observa que sus vecinas m�s cercanas no est�n dispuestas de manera irregular, sino que obedecen a un arreglo que guarda cierta semejanza con el orden geom�trico que se observa en el mismo material en fase s�lida. Sin embargo, a medida que nos alejamos de la mol�cula escogida, las vecinas pr�ximas m�s cercanas exhibir�n menos orden y a distancias de unos cuantos di�metros moleculares, la disposici�n de las mol�culas es m�s o menos al azar. Por ello se dice que los l�quidos exhiben solamente "orden de corto alcance". Esta distancia, donde se pierde el orden semejante al del s�lido, se va reduciendo paulatinamente a medida que aumentamos la temperatura. Y desde luego, se pierde totalmente cuando el l�quido empieza a evaporarse.

�C�mo podemos ahora pensar sobre lo que es la presi�n o la energ�a cin�tica promedio por mol�cula en el l�quido? Evidentemente la relaci�n tan sencilla que pudimos establecer entre ellas en el modelo cin�tico simple del cap�tulo anterior ya no se va a cumplir. La presencia de las fuerzas atractivas debe dejarse sentir. Y en efecto, as� ocurre pues la contribuci�n m�s importante proviene de que en el l�quido el empaquetamiento entre las mol�culas es m�s intenso que en el gas. Aunque los argumentos necesarios para cuantificar estos efectos est�n fuera del alcance de este libro.

Ahora bien, la energ�a cin�tica promedio por mol�cula tambi�n se modifica. En los l�quidos, el empaquetamiento entre las mol�culas tambi�n da una contribuci�n adicional a la energ�a total de las mismas. Su energ�a es, pues, no s�lo cin�tica. Adem�s, en el caso de l�quidos formados por mol�culas complicadas, �stas pueden realizar movimientos de vibraci�n y rotaci�n que a su vez generan contribuciones a la energ�a total. Uno de los problemas de actualidad en la teor�a de los l�quidos simples es encontrar la forma adecuada, tanto de la fuerza interat�mica como funci�n de la distancia, como de otros factores caracter�sticos de la estructura molecular que den lugar a valores te�ricos de la presi�n y la energ�a interna de un gas, los cuales sean simult�neamente consistentes con los valores experimentales. Y hablamos aqu� de l�quidos simples porque este programa todav�a no se ha llevado a cabo completamente para l�quidos como el nitr�geno, el arg�n, etc. Para otros, como el agua, el benceno, el tetracloruro de carbono, esto es, l�quidos m�s complejos, el problema es bastante m�s complicado.

EQUILIBRIO L�QUIDO-VAPOR-EVAPORACI�N

Ahora que ya tenemos una idea cualitativa de la diferencia por medio de la cual podemos visualizar a un l�quido y a un gas desde el punto de vista molecular, intentemos comprender c�mo es que se puede cambiar de una fase a la otra y viceversa. Empecemos por considerar dos l�quidos, por ejemplo, agua y �ter; los cuales se colocan en sendos recipientes que est�n en contacto con el aire de la atm�sfera. En cada uno de estos l�quidos las mol�culas se mueven con velocidades diferentes, en todas direcciones y a mayores velocidades unas que otras. En un instante dado, aqu�llas con velocidad suficiente para sobreponerse a las fuerzas atractivas que ejercen sobre ellas las mol�culas vecinas y que est�n suficientemente cerca de la superficie pueden escapar a la atm�sfera. En el caso del �ter eso es precisamente el mecanismo que nos permite percibir su aroma. Esta p�rdida de mol�culas más r�pidas produce eventualmente que el l�quido se evapore; como las mol�culas m�s lentas son las que van quedando rezagadas en el l�quido, la evaporaci�n hace que �ste se enfr�e. Adem�s, en nuestro ejemplo el �ter se evapora con mayor prontitud, puesto que las fuerzas intermoleculares atractivas entre las mol�culas del �ter son m�s d�biles que las correspondientes del agua; de aqu� que puedan escapar en mayor n�mero (Nuevamente: Figura 13).

Imagine el lector ahora que repetimos el mismo experimento, pero manteniendo al agua y al �ter en recipientes herm�ticamente cerrados. M�s a�n, podr�amos pensar que antes de cerrar dichos recipientes removemos el aire que queda sobre la superficie del l�quido. Por supuesto, no podremos removerlo del todo, pero supongamos que lo hemos hecho con la eficiencia suficiente como para que las pocas mol�culas de aire que ah� queden no interfieran sustancialmente con el proceso que deseamos examinar.

Va a ocurrir de nuevo lo que relatamos en el p�rrafo anterior, excepto porque ahora las mol�culas de cada uno de los l�quidos no pueden escapar: chocar�n entre s� y con las paredes del recipiente y, eventualmente, algunas de ellas empezar�n a regresar al l�quido. En consecuencia, �ste no se enfriar� y el proceso continuar� hasta que se alcance el punto en que el n�mero de mol�culas que salgan del l�quido por unidad de tiempo y unidad de superficie sea igual al n�mero que retorne. A la temperatura a la que ese equilibrio se alcance y obviamente el l�quido ya no se enfr�a, decimos que est� en equilibrio con "su vapor". Aqu� el vocablo vapor se usa como un sin�nimo de gas, derivado de la falsa idea de que vapor es un gas que condensa, esto es, que se convierte en l�quido. En estas condiciones las mol�culas de la sustancia que se encuentran sobre la superficie del l�quido forman un gas que ejerce una presi�n sobre ella. Esta presi�n depender� claramente de la temperatura. A la temperatura a la cual la rapidez de evaporaci�n del l�quido es igual a la rapidez de condensaci�n del gas, la presi�n que �ste ejerce sobre el l�quido se conoce como la presi�n de vapor. Como podr� apreciar el lector, esta presi�n es una medida de la facilidad con que pueden escapar las mol�culas del l�quido a trav�s de su superficie. De aqu� que podamos decir que la presi�n de vapor del �ter es mayor que la presi�n de vapor del agua.

Vamos ahora a repetir el experimento un poco a la manera cotidiana de un ama de casa cuando pone agua a hervir en una cacerola abierta. S�lo que nosotros quitaremos la tapa de nuestros recipientes y calentaremos lentamente los l�quidos. �Qu� ocurre? Si pensamos que en el l�quido todav�a una fracci�n de la energ�a media de una mol�cula es energ�a de traslaci�n proporcional a la temperatura, al calentar los l�quidos la energ�a suministrada por la parrilla o el mechero con que estemos calentando va a aumentar la energ�a cin�tica promedio de las mol�culas facilitando su escape a trav�s de la superficie. Esto no nos es desconocido; el calor ayuda a la evaporaci�n. Es m�s, llegar� un momento en que comencemos a ver como el gas forma una nubecilla blanca sobre el l�quido, lo que usualmente l�amamos vapor. Si dejamos de calentar ambos l�quidos a intervalos de tiempo sucesivos, tapamos los recipientes y medimos la presi�n, observaremos que �sta aumenta r�pidamente con la temperatura. Y lo que todos sabemos, llegar� un momento, caracterizado por una temperatura que es diferente para cada l�quido, en que todas las mol�culas del l�quido parecen tener suficiente energ�a para evaporarse. Este momento se manifiesta por la aparici�n de burbujas en todo el seno del l�quido. En estas condiciones la presi�n del vapor es igual a la presi�n atmosf�rica del lugar, en que estamos; decimos entonces que el l�quido hierve. Este es el fen�meno conocido como ebullici�n. A la temperatura a la que ocurre la ebullici�n las part�culas del l�quido tienen en promedio la suficiente energ�a como para contrarrestar las fuerzas atractivas y sobreponerse a la presi�n que ejerce la atm�sfera, el aire, sobre la superficie del l�quido. En el caso del agua, a nivel del mar, donde la presi�n es de una atm�sfera 760 mm de Hg, �sta hierve a 100�C. En la ciudad de M�xico, donde la presi�n es de s�lo 586 mm de Hg, hierve a 96�C. Por lo tanto, el punto de ebullici�n de un l�quido est� definido como la temperatura a la cual su presi�n de vapor es igual a la presi�n atmosf�rica local (Figura 14).

Figura 14. Ebullici�n. El calor suministrado por la combusti�n del gas en el mechero permite a un l�quido hervir cuando la presi�n de vapor ejercida por el vapor es igual a la presi�n atmosf�rica. La temperatura del l�quido y del vapor es la misma, T.

Obs�rvese tambi�n que, independientemente de que la ebullici�n ocurra en un recipiente de manera espont�nea o con la ayuda de una fuente de calor; la formaci�n de vapor de un l�quido requiere de una cierta energ�a. En el primer caso la energ�a la suple el propio l�quido, pues �ste se enfr�a al perder las mol�culas m�s energ�ticas. En el otro, la energ�a la suministra la corriente el�ctrica que usamos para la parrilla o el combustible (gas dom�stico) que quemamos en el mechero. As�, para evaporar 1 kg de agua l�quida requerimos de 540 kilocalor�as (kcal) a 100�C y de 1 atm de presi�n, o sea en el punto de ebullici�n. En este caso, la temperatura de ambos, l�quido y gas, es la misma; esto nos lleva a preguntarnos: �cu�l es el uso de esa energ�a? Como la temperatura es la misma, la energ�a cin�tica media tambi�n es la misma para todas las mol�culas, est�n en la fase l�quida o en la gaseosa. De aquí que la respuesta sea obvia: la energ�a se consume en separar a las mol�culas unas de otras en el l�quido. Ah� est�n fuertemente ligadas por las fuerzas intermoleculares atractivas, y sus distancias de separaci�n son pequeñas. Como vimos en la figura 12, si la distancia entre dos mol�culas es la distancia denotada por r_m en la figura, es necesario para separarlas gastar una energ�a que depende de la profundidad de la parte atractiva de la fuerza denotada por F_o en dicha figura. Cuando el gas se condensa, las mol�culas que penetran al seno del l�quido son "capturadas" por otras a trav�s de la acci�n de estas fuerzas atractivas. Al hacerlo pierden energ�a que se transmite en forma de calor a los alrededores

LA FASE S�LIDA. FUSI�N

La diferencia fundamental entre un s�lido cristalino y un l�quido es que en el primero existe el "orden de largo alcance". Esto quiere decir que las fuerzas intermoleculares son mucho m�s intensas en el s�lido que en el l�quido, al grado de que las part�culas en aqu�l ya no tienen libertad alguna de moverse. Como encontr� von Laue en sus experimentos de 1912, forman un patr�n geom�trico regular; por lo menos en los que forman cristales. En los que as� lo hacen, las part�culas est�n dispuestas a lo largo de l�neas y de planos igualmente espaciados entre s�. Una part�cula en el cristal est� a la misma distancia que sus vecinos m�s cercanos (Figuras 15 y 16). Por eso es que a simple vista las caras de un cristal son lisas y sus �ngulos son agudos. Pero, �est�n en reposo los �tomos en el cristal? No. El lector puede imaginar que, en cada sitio de la red cristalina ocupado por un �tomo �ste vibra incesantemente en tres direcciones mutuamente perpendiculares entre s�, como si fuera jalado por otros tantos resortes fijos en los �tomos vecinos. Este movimiento est� provocado por la resultante de todas las fuerzas que el resto de los �tomos del cristal ejercen sobre el �tomo que estamos examinando. As� pues, en un s�lido cristalino los �nicos movimientos que pueden ejecutar los �tomos que lo componen son movimientos de vibraci�n. En esta fase de la materia no hay colisiones entre las part�culas, de manera que los argumentos b�sicos de la teor�a cin�tica que hemos empleado con tanto �xito en el caso de l�quidos y gases no tienen mucha relevancia para describir a los s�lidos. En ellos la caracter�stica esencial para comprender sus propiedades m�s relevantes en t�rminos de su composici�n at�mica es, precisamente, las simetr�as inherentes a sus formas geom�tricas.

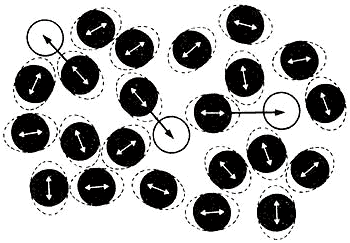
Figura 15 A: En un l�quido las moleculas que oscilan entre sus vecinos pueden escapar de la jaula de sus vecinos m�s cercanos para ser atrapadas en otra jaula.

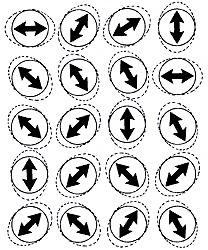
Figura 15 B: En un s�lido las m�leculas o �tomos vibran u oscilan alrededor de sus posiciones de equilibrio sin llegar a chocar entre s�. ...

Figura 16. Patr�n obtenido por difracci�n de rayos X de (a) hielo policristalino y (b) del agua l�quida.

Sin embargo, conviene mencionar que no todos los s�lidos en la naturaleza forman cristales en la forma que lo hemos descrito. De hecho, independientemente de que los s�lidos exhiban caras cristalinas, como la sal de cocina, el cuarzo, el diamante y otros, el an�lisis por rayos X muestra que su estructura interna exhibe un patr�n regular. A todos lo s�lidos que muestran estra estructura con independencia de que su aspecto externo sea o no de un cristal, se les llama s�lidos cristalinos. Tal es el caso de los ya citados arriba y de la mayor parte de los metales. Pero existen materiales que presentan el aspecto de un s�lido y que sin embargo su estructura es un tanto irregular. A �stos se les conoce como s�lidos amorfos. Ejemplos t�picos son el hule, el pl�stico, el vidrio, etc�tera.

A pesar de que en el s�lido la teor�a cin�tica no tiene tanta relevancia como en las fases fluidas, l�quida y gaseosa, todav�a nos permite entender cualitativamente la transformaci�n molecular que tiene lugar en el fen�meno de la fusi�n. Todos sabemos que para fundir un s�lido, sea hielo o cualquier otro, hay que suministrarle energ�a, por lo general, en forma de calor. �En qu� se utiliza esta energ�a? La respuesta es un tanto obvia si el lector recuerda que la diferencia entre un s�lido y un l�quido radica en que, en el primero, las fuerzas intermoleculares atractivas generan, debido a su naturaleza, un orden de largo alcance manifiesto en la estructura geom�trica regular del s�lido, mientras que en el segundo, esta regularidad s�lo se conserva entre los vecinos m�s cercanos, por lo que le hemos llamado de corto alcance. As� pues, a medida que calentamos el s�lido, la energ�a suministrada se emplea en aumentar las amplitudes de las vibraciones de los �tomos alrededor de sus posiciones de equilibrio. Cuando esta energ�a es suficiente, algunos de ellos rompen, por decir as�, sus ligaduras y empiezan a crear un desorden local en la l�tiz cristalina. Cuando este desorden se propaga m�s all� de unos cuantos di�metros moleculares y s�lo se conserva el orden "de corto alcance", el s�lido se convierte en un l�quido (ver Figura 15(b)). Parte de la energ�a potencial almacenada en los �tomos en la fase s�lida empieza a transformarse en energ�a cin�tica traslacional, caracter�stica de la fase l�quida. La cantidad de energ�a por kilogramo-mol de s�lido necesaria para llevar a cabo esta transici�n se conoce como calor de fusi�n. Para el agua es de 80 kcal por kg-mol. Es claro que �sta es la energ�a que un l�quido transfiere a sus alrededores cuando se solidifica.

Aunque en forma cualitativa y sin mayores presunciones, la teor�a cin�tica nos permite comprender, no s�lo el comportamiento molecular de la materia en sus tres fases, sino tambi�n a qu� peculiaridades de su composici�n se deben las transformaciones entre las diferentes fases. Aqu� no hemos abordado el problema completo, pues hay l�quidos complejos como los sobre enfriados, polim�ricos, cristales l�quidos y otros, as� como los s�lidos amorfos, que hemos dejado fuera de esta discusi�n. Dado que su importancia es tan especial, merecen un tratamiento aparte. Quiz�s otro volumen de esta serie sea dedicado a tan fascinante tema.