IX. LA ENTROPÍA COMO UNA MEDIDA DEL DESORDEN MOLECULAR

NO PODÍAMOS dejar pasar por alto tan controvertida, tan difundida y hasta tan mal empleada afirmación de que la entropía es una medida del desorden molecular. ¿Podemos realmente de una manera más o menos clara y objetiva asociar a esta función termodinámica una connotación tan sutil? Lo primero que quizás se nos ocurra pensar es que el desorden es una alteración del orden. Pero, ¿qué es orden? Si se recurre al diccionario veremos una página completa llena de las diferentes definiciones de este vocablo. Algunas de las más relevantes para los propósitos que se persiguen aquí son, por ejemplo: colocación de las cosas en el lugar que les corresponde; concierto de las cosas entre sí; regla o moda; sucesión de las cosas, etc. ¿Cuál elegimos o elige la naturaleza para caracterizar a la entropía? Piense el lector por unos instantes en lo que concebiría como orden en un caso muy concreto y que muchos padecemos por varias horas al día: el tráfico en la ciudad de México. ¿Qué entendemos por orden en este caso? ¿Todos los autos debidamente estacionados y las calles vacías? Podría ser. ¿O quizá el "régimen congelado de tránsito" provocado por embotellamiento tal que los autos, si se mueven, lo hacen todos en fila frustrando así a nuestros potenciales cafres del volante de ir zigzagueando por todos los carriles? ¿O mejor concebimos el orden como el tráfico fluido y coordinado, provocado por un sistema racional de semáforos que debidamente programados permiten la circulación a una velocidad promedio razonable sin mayores obstáculos? Claramente podríamos pensar en otras situaciones ideales, inexistentes desde luego en esta gran ciudad, para concebir teóricamente lo que entenderíamos por un régimen "ordenado" de tráfico. Vea y medite pues el lector que el concepto de orden es muy subjetivo: lo que puede ser orden para un grupo de personas, muy posiblemente no lo es para otro grupo. Las frases, ojalá coherentes, que he escrito en estos párrafos proyectarán una imagen de orden si las comparamos con lo que se obtendría si ponemos a un simio a teclear en una máquina de escribir. Pero claro, podrían no parecer tan ordenadas si a su vez las comparamos con un escrito de Jorge Luis Borges o un poema de Pablo Neruda. Bien, el punto está ya bastante claro: si queremos hablar de desorden, primero tenemos que dar uno, o varios criterios para definir lo que entendemos por orden. Y esto es precisamente lo que hizo Shannon en 1949: dio los criterios necesarios para medir el desorden con respecto a otro conjunto de criterios prescritos que definen un concepto de orden. Ilustremos esto con un ejemplo: a un niño cuyos padres salen de su casa se le dice que espere en una recámara mientras vuelven. Permanecer en esa recámara es la regla que define el orden en este caso. Pero claro está, el niño no la obedece; durante todo el lapso que sus padres están fuera deambula sin cesar por toda la casa y podemos suponer que permanecerá en cada habitación de ella por una fracción de tiempo determinado. Ahora bien, si se conoce la distribución, es decir, estas fracciones de tiempo que se pasó el niño en cada una de ellas, se puede, como lo hizo Shannon, cuantificar el desorden. En esta cuantificación se prescribe necesariamente la condición de que si la fracción de tiempo gastada corresponde a la estancia de la criatura en una sola habitación, el desorden es igual a cero, o bien el orden es la unidad. Lo interesante del método de Shannon es que si uno aplica estos criterios al concepto de entropía para un sistema cerrado, repetimos, un sistema que no intercambia materia con sus alrededores, se obtiene un resultado interesante: la entropía corresponde justamente a la medida cuantitativa del máximo desorden posible del sistema.

Para comprender esta afirmación regresemos de nuevo a nuestro modelo cinético. En el capítulo III hicimos notar con todo detalle que si tuviéramos la necesidad de caracterizar a cada una de las moléculas que lo componen, en un instante de tiempo determinado, sería necesario conocer seis números: tres para especificar su posición respecto a un sistema de coordenadas y otros tantos para especificar los tres componentes de su velocidad. Estos espacios determinan, en conjunto, otro de seis dimensiones imposible de pintar o de imaginar que suele llamarse el espacio fase de la molécula. A cada molécula del gas en cada instante de tiempo le corresponde un punto en este espacio. De manera que al enjambre de moléculas que lo constituyen les corresponden otros tantos puntos en dicho espacio. Podemos así representar el movimiento de las moléculas en el gas por trayectorias descritas por sus correspondientes puntos en este espacio de seis dimensiones. Si "imaginamos" a cada uno de estos espacios tridimensionales, el de posiciones y el de velocidades, proyectados sobre una recta, tendríamos una "imagen" visual de lo que ocurre en el gas, como se ilustra en figura 20. Obsérvese en ella que el espacio de las posiciones está acotado por las dimensiones finitas del recipiente que contiene el gas, y que las posiciones de las moléculas están limitadas por las tres longitudes características del recipiente, por ejemplo, los tres lados de un paralelepípedo, si es que la caja tiene esa forma. En cuanto al espacio de velocidades está acotado porque la suma de las energías cinéticas de las moléculas tiene que ser igual a la energía total del gas, a la cual podemos suponer constante si el sistema está aislado de sus alrededores. Y con esta breve introducción llegamos al punto esencial del argumento: las N moléculas del gas, como el niño libre en la casa, cambian constantemente de posición y velocidad debido a las colisiones entre ellas. Y así como el niño pudo recorrer las diferentes habitaciones pasando una fracción del tiempo total en cada una de ellas, estas moléculas en un intervalo de tiempo dado pueden pasar por varios estados, aquí definidos por las posiciones y las velocidades y una fracción de ese intervalo de tiempo en dichos estados. Ahora olvidémonos del tiempo suponiendo que el gas está en equilibrio y que por lo tanto cualquier observación que hagamos sobre cualquiera de sus propiedades medibles, como presión, temperatura, etc., va a ser la misma independientemente del tiempo. Esta independencia, repetimos, caracteriza a los estados de equilibrio. Uno se puede hacer entonces la pregunta: ¿cuántos estados microscópicos les son accesibles a las moléculas? La respuesta es evidente: muchísimos; de hecho, todos aquellos que son compatibles con los valores E de la energía y V del volumen. ñSon todos los puntos posibles encerrados en el rectángulo de la figura 20! Al niño, en el ejemplo anterior; sólo le eran accesibles las recámaras (estados) de la casa en que se encontraba. Pero en el estado de equilibrio del gas uno podría preguntarse si de todos los estados accesibles a sus moléculas no hay un conjunto de ellos que les sea más favorable, esto es, estados que sean visitados con mayor frecuencia por las moléculas. La respuesta a esta pregunta es afirmativa. Más aún, se puede calcular este número y mostrar que depende de la energía E, el volumen V y el número N. En 1872 el físico austriaco Ludwig Boltzmann llegó a un resultado muy importante. Partió del hecho de que en un sistema aislado y en equilibrio la llamada segunda ley de la termostática puede hacer ver que la entropía es un máximo consistente con las restricciones impuestas al sistema. En el caso del gas en cuestión, la entropía es máxima para la energía E y el volumen V los cuales son constantes. Por otra parte, desde el punto de vista microscópico, el estado de equilibrio está asociado, como acabamos de mencionar, con el número de estados microscópicos que determinan la distribución más probable de las moléculas en ellos. Boltzmann supuso entonces que debería haber una relación entre la entropía y esta distribución más probable. De esta manera llegó a su celebrada fórmula: "la entropía S es igual a k veces el logaritmo natural del número de estados microscópicos que determinan la distribución más probable". En esta fórmula k es una constante que pudo identificarse después como R/N_o, la constante de Boltzman, citada en el Apéndice 3.

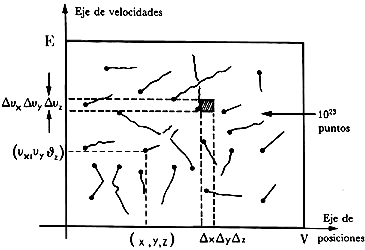
Figura 20. Cada punto en el rectángulo determinado por E (energía) y V (volumen) corresponde a una molécula del gas en un instante dado determinado por seis números, tres (x, y, z) corresponden a su posición y tres (V_x V_y V_z) a su velocidad. Hay 10²³ puntos moviéndose en esa región de acuerdo con las leyes de la mecánica.

Lo sorprendente del resultado es que en la teoría de Shannon esta distribución más probable corresponde justamente al estado en el cual "el desorden" es máximo. De aquí se infiere lo que real y objetivamente podemos asociar como una medida del desorden a una cantidad termostática, a saber, la entropía. En efecto, "para un sistema cerrado la entropía corresponde a la medida cuantitativa introducida por Shannon sobre lo que es el mayor desorden posible en la distribución de un sistema, e.g. las moléculas del gas en sus posibles estados microscópicos". Es, pues, así como surge la interpretación habitual de la entropía como una medida del desorden molecular. Entre mayor sea el número de estados de que dispongan las moléculas para distribuirse en ellos cuando el sistema está en equilibrio, mayor será el "desorden molecular". Y con esta asociación de ideas, una de origen estrictamente termostático, la entropía, y otra de origen estadístico, la distribución de las moléculas en sus microestados, se da a la primera una connotación estadística. Vea el lector que esta asociación ya ocurrió una vez: la temperatura se interpreta en términos de la energía cinética promedio por molécula. En la interpretación molecular de las propiedades termostáticas de un sistema formado por muchas moléculas, las cantidades como la entropía y la temperatura que no tienen un origen estrictamente mecánico, intervienen por la necesidad misma a partir de un ingrediente de naturaleza estadística.

Con esta nueva forma de visualizar a la entropía, que por cierto puede hacerse extensiva a sistemas en los cuales puede existir intercambio de materia y energía con los alrededores, el lector podrá apreciar varias aseveraciones que suelen hacerse con frecuencia. Por ejemplo, es común referirse a un sólido como un sistema más ordenado que un líquido, el que a su vez es más ordenado que el gas. Por lo tanto, las entropías son, respectivamente, mayor en el gas y menor en el sólido. De acuerdo a la interpretación discutida en el párrafo anterior; esto es muy creíble. En un sólido (ver Figura 15(b)), las moléculas no tienen movilidad alguna, pues están fijas a un sitio de una látiz y sólo pueden vibrar como resortes alrededor de su posición de equilibrio. Evidentemente el número de estados microscópicos accesibles a ellas es mucho menor que en el caso del gas. En el líquido la situación es intermedia, pues como vimos en el capítulo VI a pesar de que hay orden de corto alcance, las moléculas llegan a chocar y pueden desplazarse de un punto a otro, aunque siguiendo un camino más tortuoso que en el gas. De aquí que la relación entre las entropías sea la mencionada líneas atrás.

Este tipo de razonamiento llevo a muchos físicos de principios de este siglo a pensar que al enfriar la materia cada vez más, la menor accesibilidad de las moléculas a diversos estados microscópicos nos llevaría a un orden perfecto. Según esto, al enfriar un gas, éste se licua y finalmente, se solidifica, y lo hace de manera tal que al llegar a temperaturas muy bajas las vibraciones de las moléculas alrededor de sus posiciones de equilibrio serían cada vez menores, hasta que al final los espines de los núcleos de que están formadas se alinearían de tal forma que se produzca un cristal caracterizado por un orden perfecto. Por lo tanto, todo estaría "en su lugar" y en consecuencia su entropía sería igual a cero. Esto llevó a Max Planck a postular en 1917 que la entropía de todo sistema debe ser cero en el cero absoluto. Sin embargo, el experimento mostró rápidamente que en la naturaleza esto no sucede así. Al enfriar un sólido más y más, no todas las moléculas "caen" a su posición natural ni los espines nucleares se alinean como uno esperaría y, por éstas u otras causas, muchos sólidos exhiben una entropía residual a temperaturas muy bajas. Por ello decimos que conservan un cierto "desorden molecular". Este hecho ha contribuido mucho a esclarecer el comportamiento de la materia a bajas temperaturas y, sobre todo, a mostrar la naturaleza necesariamente microscópica de cualquier enunciado de una regla que, como la de Planck, pretenda generalizar el comportamiento de la materia en el cero absoluto.

Sobre el mismo tema es interesante mencionar que en las últimas décadas se han logrado avances notables en nuestro conocimiento sobre materiales más complejos que los sólidos cristalinos. Los vidrios, el hule, ciertos plásticos y otros materiales similares, están formados por moléculas muy complicadas que, como ya dijimos, los clasifica como sólidos amorfos. Por muchos años se ha pensado que un sólido amorfo, el vidrio, por ejemplo, es un estado metaestable que se forma en circunstancias muy peculiares. Sin embargo, si el tiempo es suficientemente largo, llegaría a su estado estable, esto es, a adoptar su estructura cristalina. Ahora, a raíz de múltiples estudios hechos fundamentalmente con vidrios formados por moléculas poliméricas, se ha encontrado que existen sólidos amorfos que permanecen como tales aun a las más bajas temperaturas. Estas moléculas poliméricas que en general son cadenas largas de forma muy irregular es difícil que logren formar un conglomerado regular aun a las temperaturas más bajas. Esto implica que siempre existirá una entropía residual y por lo tanto un desorden molecular cerca del cero absoluto. Es muy probable que la naturaleza nos tenga reservadas grandes sorpresas a medida que estudiemos con más detalle a estos sólidos y algunos líquidos tan peculiares como aquéllos.