X. TEORÍA CINÉTICA MODERNA

HEMOS hecho mención varias veces a que el modelo cinético de un gas ideal, que ha servido para ilustrar las ideas principales manejadas en esta obra, da resultados que para gases di y poliatómicos no concuerdan con el experimento. Además, los coeficientes de transporte calculados a partir de sus premisas sólo concuerdan cualitativamente con éste. ¿Cuál es entonces el estado actual de esta teoría, sobre todo para gases densos y líquidos? ¿Es un campo agotado o es un problema abierto? La respuesta a estas interrogantes y otras similares es, para los que vivimos a finales del siglo xx, un tanto sorprendente. Veamos por qué.

A pesar de que fueron Rudolf Clausius y James Clerk Maxwell los dos grandes pioneros de la conceptualización de la teoría cinética tal y como la hemos presentado aquí, fue Ludwig Boltzmann quien en 1872 sentó las bases de lo que hoy podríamos llamar la teoría cinética moderna. Su contribución no sólo fue copiosa en ideas y conceptos, sino que los resultados fundamentales contenidos en su teoría todavía hoy en día, 114 años después, no han sido superados. Boltzmann, en su trabajo original, usó un modelo muy parecido al planteado aquí en el capítulo III. Consideró un gas formado por esferas duras y suficientemente diluido para que sólo ocurran, de manera relevante, colisiones binarias entre ellas. Esta dilución tiene como idea imitar el comportamiento de un gas a bajas densidades, en el cual las colisiones en que intervengan simultáneamente tres o más partículas, sea tan remotamente improbables que puedan despreciarse. Además, en lugar de suponer una distribución uniforme de partículas, sustituye ésta y las hipótesis cuatro y cinco del capítulo III por una ecuación íntegro-diferencial que establece la forma cómo evoluciona con el tiempo la función de distribución de las partículas. Esta función es una medida del número de partículas que a un tiempo dado tienen velocidades comprendidas en un intervalo dado y simultáneamente posiciones en otro intervalo. Si nos referimos a la figura 20, es el número de partículas que están contenidas en un elemento de volumen Dv_x, Dv_y,Dv_z, D_x, D_y, D_z del espacio fase hexadimensional. Dicha ecuación establece simplemente que el número de partículas que entra y sale de este volumen en un cierto intervalo de tiempo, tanto por su movimiento natural como por las colisiones entre ellas debe "balancearse" entre sí. Para calcular la contribución de las moléculas por colisiones, utilizó una hipótesis probabilística muy semejante, en contenido, a la listada bajo la hipótesis cuatro del capítulo III. A dicha hipótesis se le conoce como la hipótesis del "caos molecular". La ecuación tiene, pues, un ingrediente probabilístico que proviene, como en la anterior hipótesis, de nuestra impotencia para poder seguir la dinámica individual de cada molécula en un gas formado por N (~10 ²³) de ellas.

De esa ecuación extrae Boltzmann dos resultados que han marcado la ruta de todo el desarrollo del pensamiento contemporáneo en la teoría microscópica de procesos dependientes del tiempo. El primero es que construye una función que, a la Shannon, es una medida del desorden molecular instantáneo en el gas y muestra que en el transcurso del tiempo, en su valor promedio, esta función nunca puede aumentar. Esto es, el "negativo del desorden molecular" debe tender a un máximo. El valor máximo para un sistema cerrado ñes precisamente igual al valor de la entropía termostática! Esa función entonces, no como función termostática, sino como una medida del valor negativo del desorden molecular, se puede interpretar como un criterio de irreversibilidad. La tragedia de esta conceptualización es que se ha tendido siempre a extrapolar el concepto termostático de entropía a situaciones fuera de equilibrio con base en este resultado y esto es incorrecto. La interpretación es justa y real si a lo que llamamos entropía fuera de equilibrio es una medida del desorden molecular a la Shannon. Pero ésta no se apreciaba en ese entonces y se aceptó tácitamente que el resultado de Boltzmann era equivalente a probar la segunda ley de la termostática "fuera de equilibrio". ñEsto es totalmente falso! La entropía termostática concebida como una función bien definida de las variables termodinámicas, digamos la energía E y el volumen V, para un sistema aislado sólo tienen sentido en equilibrio; y sólo entre dos estados de equilibrio su diferencia será no negativa. Pero fuera de él la desigualdad mostrada por Boltzmann sólo tiene sentido si interpretamos a la entropía como una medida del desorden molecular y este desorden, como acabamos de mostrar en el capítulo anterior, es máximo precisamente en el estado de equilibrio, si el sistema es un sistema aislado. Y muestra, además, que en este estado la función de distribución de velocidades es precisamente la distribución de Maxwell (ver Figuras 9 y 10).

El segundo resultado de Boltzmann es que logra deducir las ecuaciones de conservación de la masa, el ímpetu y la energía, de su ecuación general. Mas la enorme ventaja de esta deducción es que las expresiones para el flujo del ímpetu (tensor de los esfuerzos) que aparece en la segunda y el flujo de energía (calor) que aparece en la tercera de dichas ecuaciones, sólo dependen de los parámetros que caracterizan a las moléculas del gas, como su masa, su carga (si es un gas cargado eléctricamente), etc., y de la función de distribución de las moléculas. Esto es, el cálculo explícito de estas cantidades puede llevarse a cabo si se sabe obtener la solución de la ecuación de Boltzmann en un instante dado. Es pertinente notar que, en forma diferente y un tanto oscura, estos resultados habían sido obtenidos por Maxwell en 1867.

Tuvieron que transcurrir muchos años antes de que estos resultados fueran reconocidos. Prácticamente él se pasó los últimos años de su vida, que culminaron con su suicidio en 1906, intentando convencer; sobre todo a la escuela alemana de energeticistas encabezada por Ernest Mach y Wilhelm Ostwald, además de otros, que se oponían a teorías microscópicas de la materia. Sin embargo, la solución de la ecuación de Boltzmann tuvo que esperar todavía otros años más. En 1912 el gran matemático alemán David Hilbert se interesó en la ecuación por considerarla un caso típico de las ecuaciones integrales que él estaba estudiando. Así propuso un método muy general y elegante para resolverla que no tuvo mucha repercusión en ese entonces. Fue en 1917 cuando un sencillo profesor de secundaria sueco, David Enskog, aplicó el método de Hilbert en forma muy explícita y pudo calcular, gracias a un método que ahora lleva su nombre, la forma de la función de distribución dependiente del tiempo de manera explícita. Al evaluar las expresiones encontradas por Boltzmann para el flujo de ímpetu y el flujo de calor obtuvo, en una primera aproximación, las ecuaciones de Newton y de Fourier mencionadas en el capítulo VII. Automáticamente se obtienen fórmulas explícitas para la viscosidad y conductividad térmica, las cuales son más complicadas que las obtenidas con el modelo sencillo del capítulo VII, pero que corroboran, como ahí se mencionó, su dependencia con la raíz cuadrada de la temperatura. los resultados mostrados en la figura 19 están calculados por medio de las fórmulas de Enskog. Estos resultados fueron deducidos en forma totalmente independiente en 1919 por el matemático inglés Sidney Chapman, quien utilizó el método de Maxwell para llegar a ellos. Por ello a este método se le conoce ahora como el método de Chapman-Enskog.

Este método para resolver la ecuación de Boltzmann es tan sorprendentemente poderoso, que prácticamente desde las fechas en que se gestó, hasta el principio de la década de los cincuenta fue utilizado de manera exhaustiva para calcular coeficientes de transporte en gases diluidos. Así mismo, el uso de la ecuación de Boltzmann ha sido aplicado con un éxito enorme en campos muy diversos, como el transporte de electrones y fotones en sólidos, el cálculo de coeficientes de difusión mutua en mezclas multicomponentes, en las ecuaciones de transporte en superfluidos y superconductores, en la teoría de transporte en fluidos ionizados (plasmas), en reacciones químicas y en muchos otros casos, largos de enumerar. En cuanto a su estructura formal, se ha usado para dar una fundamentación microscópica a la termodinámica de procesos irreversibles, tanto en su versión lineal iniciada por T. de Donder y L. Onsager a fines de la década de los treinta, como en la versión ahora llamada extendida, iniciada por Lebón, Casas-Vázquez, Jou y otros, en Europa, y por un grupo encabezado por el autor de este libro, en México.

¿Cómo ha evolucionado esta disciplina de la física en los últimos 35 años? El hecho de que la ecuación de Boltzmann constituye sólo un modelo para gases diluidos fue reconocido desde el siglo pasado. Pero no fue sino hasta 1922 cuando el propio Enskog propuso un método semiempírico para generalizar la ecuación de Boltzmann para fluidos densos, en fase gaseosa o líquida. La idea de Enskog es muy simple y consiste en tomar en cuenta el hecho de que, en un gas denso formado por esferas duras, se debe tomar en cuenta el volumen excluido. Este volumen es la región del espacio que no puede ser ocupado por una tercera molécula cuando otras dos, de igual diámetro, están en contacto. Este volumen se muestra en la figura 21. El éxito de esta ecuación radica en que ha permitido, en varias versiones que de ella se tienen en la actualidad, calcular coeficientes de transporte para fluidos densos que concuerden satisfactoriamente con el experimento. Sin embargo, las variedades de esta ecuación, conocidas bajo el nombre genérico de ecuaciones de Enskog modificadas, todavía presentan algunas dificultades conceptuales un tanto técnicas para listarse aquí (ver referencia 6 para mayores detalles).

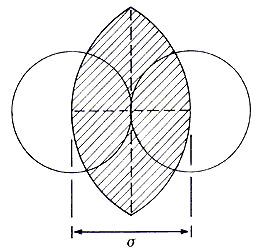
Figura 21. Volumen excluido para dos esferas duras de diámetro s-.

El obstáculo central en la teoría de los gases densos ha sido la increíble dificultad que ha presentado, conceptual y matemáticamente, el poder generalizar la ecuación de Boltzmann para incluir colisiones de más de dos moléculas. La pregunta concreta radica entonces en cómo incorporar los efectos de colisiones entre tres, cuatro y mayor número de partículas. Estas contribuciones serán obviamente más importantes a medida que la densidad del gas sea mayor. En la fase líquida misma existe ya la duda sobre si la idea misma de colisión es la más útil para describir la interacción entre las moléculas. Una ecuación de Boltzmann relativamente útil en la cual se incluyen los efectos de las colisiones triples es la obtenida en 1958 por Choh y Uhlenbeck basándose en ciertas ideas introducidas por el gran físico soviético N. N. Bogoliubov en 1949. El estudio detallado de esta ecuación para extraer de ella coeficientes de transporte ha sido un éxito gracias al esfuerzo verdaderamente titánico del grupo de J. V. Sengers, ahora en la Universidad de Maryland, en los Estados Unidos. Pero la ecuación, aunque puede generalizarse a mezclas multicomponentes como lo mostraron Cohen, Ernst y el autor en 1970, y esta generalización es compatible con la termodinámica irreversible lineal, no ha podido mostrarse que satisface un criterio de irreversibilidad como la ecuación de Boltzmann. Por otra parte, la inducción de colisiones entre cuatro o más partículas conduce ya a resultados un tanto desafortunados. Después de largos y tediosos cálculos se encuentra que los coeficientes de transporte contienen un término proporcional al cuadrado de la densidad multiplicado por el logaritmo de la densidad misma. Cuando ésta tiende a cero, el logaritmo tiende a "menos infinito"; por tanto, el coeficiente "diverge logarítmicamente", un resultado poco o nada físico y en total desacuerdo con el experimento.

Estos fracasos han obligado a los ya muy pocos físicos que se interesan en estas cuestiones, por no ser "temas de moda", a examinar de muchas maneras cuál es el origen de la ecuación de Boltzmann a partir de los principios más fundamentales de la física clásica. La respuesta a esta pregunta arrojaría luz sobre su posible generalización a fluidos densos. Pero los esfuerzos han sido, globalmente, infructuosos ya que hasta la fecha estos problemas y otros problemas con él conectados o derivados, permanecen abiertos. A pesar de los notables avances de la física en otras áreas, hoy todavía no sabemos calcular la viscosidad, u otro coeficiente de transporte, para un gas denso o un líquido a partir de primeros principios. El reto subsiste y la mayoría de los científicos le huye.