APÉNDICE 1

En este apéndice vamos a dar una demostración muy sencilla de la relación que existe entre la presión y la energía cinética promedio de las moléculas que componen un gas descrito por el modelo cinético del capítulo IV. Para ello vamos a emplear esencialmente la hipótesis 4, a saber, la que establece que todas las velocidades son igualmente posibles.

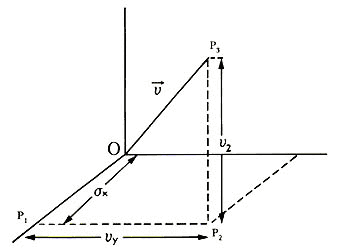
Figura 22. En un sistema de coordenadas rectangulares la velocidad de una molécula v se descompone en sus tres componentes vx, v_y y vz.

Pensemos, como podemos pensar, que están distribuidas las velocidades entre la N partículas. Como sólo hay tres componentes independientes v_x, v_y, v_z, (Figura 22) podemos imaginar que 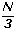partículas tienen velocidad v_x, 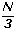velocidad v_y y v_z. Definamos una superficie en la cara del paralelepípedo que contiene al gas en el plano XZ. Las partículas que lo van a golpear son necesariamente aquellas cuya velocidad esta en la dirección vy y de ellas, según la figura 23 las que viajan de derecha a izquierda. Supongamos que ésas son la mitad de las que tienen velocidad v_y. Si la celeridad media de estas moléculas es 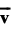chocarán contra A aquellas contenidas en el cilindro de base A y altura t. Si n es el número de partículas por unidad de volumen, el número de partículas que chocan con la superficie A en el tiempo t es:

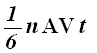
Por cada molécula que choca con la superficie el cambio en el ímpetu de la molécula es 2m.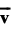

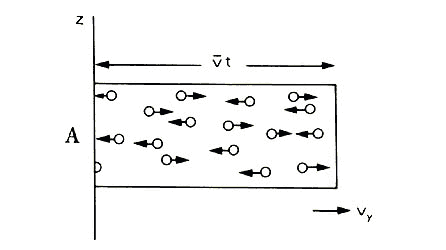
Figura 23. En esta versión supersimplificada se puede imaginar que las moleculas sólo se mueven en las diferentes vx, v_y y vz en terceras partes, de las con velocidad v_y sólo las que se mueven de derecha a izquierda chocan con la superficie A.

Por consiguiente, como la fuerza que se imprimió a la pared es el cambio de ímpetu por unidad de tiempo que se produce por todos los choques, dicha fuerza es:

y la presión, que es igual a la fuerza por unidad de área, será

y como , obtenemos resultado deseado

(A-1)

El lector debe ser muy crítico con esta demostración, ya que no es rigurosa. El resultado que se obtiene, aunque es correcto, proviene de una serie de cancelación de errores. Entre ellos está el contenido en la suposición de que, lo cual en general, no es cierto. Sin embargo, ilustra de manera cualitativa la bondad del modelo tan simple que hemos empleado.