III. EL MODELO CINÉTICO DE UN GAS

CREO que a estas alturas estamos convencidos, gracias a los experimentos de Gay-Lussac y a las ideas de Avogadro, que los filósofos griegos, Lucrecio en particular, habían acertado al pensar que la materia, y en especial los gases, están compuestos de pequeñas partículas que ahora identificamos como átomos o moléculas. Aceptemos también que estas moléculas están en movimiento constante. El conocido fenómeno del movimiento browniano fue descubierto por el botánico inglés Robert Brown en 1827 al observar que en suspensiones acuosas de esporas finas inanimadas, dichas esporas exhiben un continuo movimiento errático y caprichoso sin haber razón aparente alguna que lo produzca. Este fenómeno proporciona una evidencia experimental que soporta dicha hipótesis. El problema que se presenta ahora es, primero, cómo concebir físicamente a estas moléculas, y segundo, sobre qué bases podemos intentar analizar y describir su movimiento. Respecto a la primera cuestión, Bernoulli en su trabajo Hydrodinamica, al que nos referimos en el capítulo 1, empleó exitosamente el modelo de una esfera rígida (bola de billar) para representar a cada molécula.

Por su simplicidad, conservémoslo por el momento. Un gas es un conglomerado enorme de pequeñas bolas de billar en movimiento constante. El verdadero problema radica en encontrar la forma de describir este movimiento. Veamos por qué.

Imagínese el lector una bola de billar metida en un recinto tridimensional de forma arbitraria, en que dicha bola, digamos pintada de un color diferente que las demás, se mueve entre otras tantas bolas que en número supera los billones de billones. Imagínese también que éstas chocan entre sí y contra las paredes del recipiente, y que a pesar de ello apenas si ocupan un volumen apreciable del volumen que disponen para moverse. ñImpracticable entonces intentar seguir el movimiento de la bola roja! Y de hecho de ninguna bola individual de este enjambre. ¿Qué hacer entonces? Lo más sensato es olvidarnos de cualquier intento por caracterizar la dinámica individual de cada partícula y pensar, como lo hacen aquellos que toman censos de una población grande de individuos, en extraer algún tipo de comportamiento promedio de las bolas de billar que representan a las moléculas que componen el gas.

Comencemos por decir algo más sobre las posiciones que ocupan éstas en el transcurso del tiempo o, mejor dicho, la densidad de ellas medida en partículas por unidad de volumen. Para precisar más esta cuestión, consideremos un volumen de un litro de gas (1 000 cm^³) a presión de una atmósfera y temperatura ambiente. En dicho recipiente habrá aproximadamente 10²² moléculas. En cada cm³ del volumen podemos pensar que, de no existir un agente externo que promueva la existencia de regiones privilegiadas dentro del recipiente, siempre encontraremos del orden de 10¹⁹ moléculas. De este hecho no podemos estar completamente seguros, pero, sin embargo, parece lógico. Vamos a adoptarlo como la primera hipótesis sobre nuestro modelo cinético del gas: las partículas se distribuyen uniformemente dentro del volumen que las contiene, de manera que el número de ellas por unidad de volumen es constante. ¿Y las velocidades? Ya dijimos que las partículas están en constante movimiento chocando entre sí y con las paredes del recipiente. Vamos a suponer, como una primera aproximación, que fuera de estos choques no hay más fuerzas actuando sobre ellas: tal y como ocurre en una mesa de billar si sólo pensamos en los choques de las bolas entre sí y los de ellas contra los bordes de la mesa. Es claro que esta hipótesis es muy burda. Todos hemos oído hablar de las fuerzas interatómicas o intermoleculares que actúan entre átomos o moléculas y que obviamente existen en cualquier sustancia real. Cierto, esto es completamente correcto, pero en una primera aproximación vamos a olvidarnos de ellas. Prosigamos ahora con un análisis de los choques. En el anillo periférico de la ciudad de México, que en ocasiones parece asemejarse al modelo que estamos construyendo para el gas por lo errático y desordenado del tráfico, si chocan dos vehículos, aunque pueden salir rebotados, los daños que resienten son suficientes para detenerlos. En la colisión hay parte de absorción de energía por las carrocerías de ambos vehículos y parte que se consume por la fricción de los neumáticos con el pavimento. La energía (cinética) de los vehículos es claramente diferente antes y después de la colisión. Decimos por tanto que la colisión es inelástica. Los choques de las bolas de billar entre sí y contra las paredes presentan otra situación, pues, excepto por el cambio en la dirección de su movimiento, parecen conservar su ímpetu y su energía. Cuando concebimos una colisión, ideal desde luego, entre dos objetos de manera tal que su ímpetu (masa por velocidad), como su energía cinética (un medio de su masa por el cuadrado de su velocidad), son iguales antes y después de una colisión, decimos que ésta es elástica. Vamos a agregar esta hipótesis a nuestro modelo: a saber, las colisiones entre partículas y de éstas contra las paredes son elásticas (Figura 4).

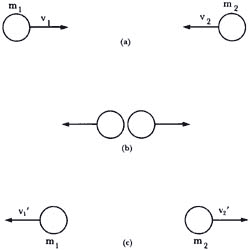
Figura 4. (a): Dos esferas duras una de masa m₁ y con velocidad v₁ y la otra con masa m₂ y velociada v₂ se aproximan antes de chocar frontalmente como en (b). (c): Las dos esferas salen rebotadas de la colisión con velocidades v₁' v₂' respectivamente. Si la colisión es elástica y escogemos positivas las velocidades de izquierda a derecha,

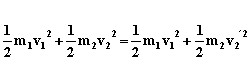
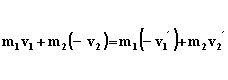
Nos falta ahora decir algo sobre las velocidades mismas. Partiendo de la hipótesis anterior podemos decir que, como sobre cada partícula no actúa fuerza alguna entre dos colisiones sucesivas, su velocidad en magnitud y dirección debe ser constante. Esta afirmación es una consecuencia directa de la segunda ley de Newton, pues si la fuerza neta actuando sobre un cuerpo arbitrario es cero, su aceleración es también nula, y por consiguiente su velocidad es constante. Esto quiere decir que en tanto una molécula no choque, se moverá siguiendo una trayectoria rectilínea, pero que debido a los choques, la dirección del movimiento cambiará incesantemente. Ahora bien, si recordamos que tenemos ñ10²² moléculas en nuestro frasco de un litro!, intentar llevar un registro de sus cambios de dirección debido a las colisiones, es un hecho, si no imposible, ciertamente impracticable. ¿Cómo resolver este problema? (Ver Figura 5.)

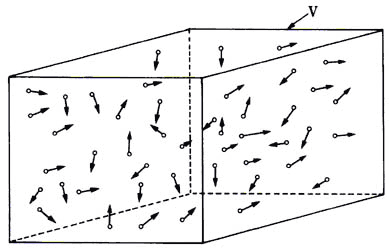
Figura 5. En un recipiente de volumen V hay N moléculas cuyas velocidades en dirección son completamente caóticas. Recordemos que N-~-10²².

A no ser que tomemos una decisión drástica para resolverlo, éste parece complicarse enormemente. Puede resultar curioso, pero esta decisión la podemos extraer de nuestra propia actitud ante situaciones mucho menos complicadas en apariencia, pero en las cuales carecemos de información suficiente para resolverlas lógica y racionalmente. Éstas se presentan en todos los juegos de azar. ¿Podemos predecir con certeza si al lanzar una moneda al aire caerá águila o sol? ¿O qué par de números se darán al tirar un par de dados de un cubilete? ¿O bien si un número dado de un billete de lotería será premiado, por ejemplo, con el premio mayor? ñCiertamente no! En nuestra participación en estos juegos interviene implícita la hipótesis de que todos los posibles eventos del juego tienen la misma posibilidad de ocurrir. Aunque no lo meditemos, en el momento de jugar estamos aceptando esta igual posibilidad de ocurrencia de todos los eventos posibles. Por ejemplo, existe un 50% de posibilidades que la moneda caiga águila y otro tanto que caiga sol, ñy sin embargo jugamos! Imagine ahora el lector que podemos hacer con 10 ²² moléculas cuyas direcciones en la velocidad cambian constantemente con el tiempo. La respuesta, si no obvia, es un tanto sugestiva: suponer que en todo momento cualquier dirección en la velocidad tiene iguales posibidades de ocurrir, esto es, todas son igualmente posibles. Esta hipótesis, cuyo contenido está estrechamente asociado con las características de los juegos de azar, desempeña un papel importantísimo en todas las áreas de la ciencia, y en particular en la física, donde nos enfrentamos al problema de resolver la dinámica de una gran población de partículas (~l0 ²²),* cuya solución si se busca por medio de la aplicación de las leyes de la mecánica clásica, es decir; de las leyes de Newton, si no resulta imposible, sí es altamente impracticable. Suplimos pues nuestra impotencia para abordar esta compleja situación con un modelo sumamente simple, muy semejante al de la hipótesis de la lotería. En un lenguaje más técnico, ésta se conoce como la hipótesis de probabilidades iguales a priori. De aquí, de la estadística matemática, surge entonces el inevitable probabilístico que usamos para describir y explicar el comportamiento de sistemas de N cuerpos. Es por ello que a este campo se le conoce globalmente como física estadística.

Para que el lector conserve una imagen clara y concisa del modelo que hemos construido con el objeto de representar el comportamiento de un gas, vamos a resumir las hipótesis fundamentales que lo constituyen. Ellas son:

1) El gas está formado por un conjunto de N(~10²²) m léculas concebidas por pequeñas esferas rígidas de diámetro (aproximadamente 10-⁸ cm), despreciable comparado con longitudes macroscópicas. Nótese que el volumen ocupado por una molécula es aproximadamente igual a 10-²⁴ cm³. De aquí que ocupado por 10²² moléculas sea apenas de l0^-² cm³ : ñla centésima parte de un cm³ ! Por tanto, en nuestro recipiente de 1 000 cm³ prácticamente todo el espacio está vacío.

2) En ausencia de fuerzas externas y despreciando los efectos del campo gravitacional, las moléculas están distribuidas uniformemente en el recipiente. Esto es, en todo momento número de moléculas por unidad de volumen es constante.

3) Las moléculas no ejercen fuerzas entre sí, excepto cuando sufren una colisión con otra molécula o contra las paredes del recipiente. Además, estas colisiones son elásticas.

4) Todas las direcciones de las velocidades moleculares son igualmente probables.

5) Las magnitudes de las velocidades moleculares cambian constantemente como consecuencia de los choques y, numéricamente, pueden tomar valores entre cero y una velocidad máxima que no puede exceder la velocidad de la luz.

Como el lector puede apreciar, este modelo puede aparecer como muy simple y, desde luego, poco realista. Surge de manera natural la duda acerca de las posibilidades efectivas de que podamos extraer de él algunas consecuencias que sean factibles de comparar con la evidencia experimental de que disponemos. Si la concordancia entre las predicciones del modelo y dicha evidencia son satisfactorias, juzgaremos al modelo como adecuado. Y lo será más aún en la medida que encontremos también sus limitaciones para poder mejorarlo y extenderlo a casos más generales. Por el contrario, si las predicciones no concuerdan con el experimento, entonces habrá que desecharlo. En el siguiente capítulo estudiaremos estas alternativas.