IV. LAS PROPIEDADES DE UN GAS EN EQUILIBRIO

A MANERA de preámbulo para éste y los capítulos subsecuentes, es de imperiosa necesidad hacer una breve recapitulación de aquellas propiedades, de la materia en general y de los gases en particular, que deseamos extraer de un modelo cinético como el propuesto en el capítulo anterior. La materia, como hemos insistido varias veces, la encontramos en una de sus tres fases: gaseosa, líquida o sólida; aunque en algunos casos coexisten dos de estas fases entre sí y, en condiciones muy drásticas, el llamado punto triple, las tres. Esta última posibilidad no la estudiaremos aquí.

Ahora bien, cuando examinamos las fases individualmente, se presentan en general, dos situaciones. En una estudiamos al sistema en la fase elegida en condiciones tales que sus propiedades no sean funciones del tiempo, esto es, que durante el intervalo de tiempo que dura el experimento que se empleó para determinar una cierta propiedad, el sistema no cambie. En estas condiciones decimos que la propiedad medida corresponde a lo que se conoce como una característica del estado de equilibrio de dicho sistema. Las relaciones que existen entre las diversas propiedades de sistemas en equilibrio constituye el tema central de la llamada termostática o termodinámica clásica.* Por otra parte, existe una multitud de fenómenos que ocurren cuando el sistema, perturbado por algún agente externo, no manifiesta una condición estática, sino que por el contrario dicha condición cambia con el tiempo. El flujo de gases y fluidos en general, a través de ductos; la atmósfera perturbada por el paso de un objeto, digamos un cohete o un avión; las perturbaciones meteorológicas; los movimientos de las capas terrestres; la deformación de cuerpos sólidos al someterlos a una tensión; el flujo de la sangre por una arteria; el paso del aire por las vías respiratorias; las reacciones químicas y una multitud similar de fenómenos imposibles de enumerar, constituyen ejemplos típicos de estos fenómenos. Dadas las variaciones que se observan en las propiedades de estos sistemas en el transcurso del tiempo, se les ha llamado, a los fenómenos mismos, fenómenos fuera de equilibrio. En la actualidad su estudio constituye una de las áreas, no sólo más complicadas sino, por su importancia, más activas en la física y la química.

Bien, con nuestro rudimentario modelo cinético del gas podemos pensar qué tipo de información relevante podemos extraer acerca de las propiedades del gas en equilibrio y cuáles son factibles de ser estudiadas cuando el gas se encuentra fuera de equilibrio. En este capítulo nos concentraremos en las primeras. En nuestro cotidiano contacto con las propiedades de los gases, hay dos variables que sistemáticamente utilizamos para caracterizarlos. Una es la presión, como sucede al inflar un neumático a la presión requerida, al referirnos a la presión atmosférica en un sitio determinado, al observar un manómetro que nos indique la presión del gas encerrado en un tanque, etc. Otra es la temperatura; hablamos de la temperatura del medio ambiente, la temperatura de los gases en un proceso de combustión, por ejemplo, de un motor de gasolina, etc. Y posiblemente en raras ocasiones nos preguntemos: ¿qué miden realmente los instrumentos sensores? Al poner el manómetro en contacto con la válvula de un neumático, o un medidor de Venturi en una tobera, o el manómetro mismo ajustado a la boca de un tanque conteniendo gas, ¿qué es lo que causa el desplazamiento del émbolo, el corrimiento de la aguja o el movimiento indicador de cualquiera que sea el sensor usado en la medición? Y la misma pregunta puede hacerse respecto a la temperatura: ¿qué excita al líquido del bulbo termométrico forzándolo a subir por la columna graduada? Aparte de las convenciones utilizadas para distinguir fenomenológicamente entre dos o más presiones, gases más o menos comprimidos, o dos o más temperaturas, gases más o menos calientes, ¿qué más podemos decir respecto a estas propiedades a la luz de nuestro modelo cinético?

Empecemos con la presión. Ya quedamos en que las moléculas que componen el gas en cuestión están en movimiento continuo y chocan furiosamente entre sí y contra las paredes del recipiente que las contiene. Analicemos estos choques recordando que éstos son elásticos (Figura 4). Comencemos por el caso de una molécula que choca perpendicularmente contra una pared (Figura 6).

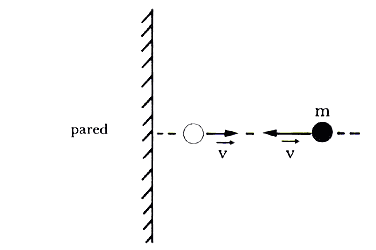
Figura 6. Si la mólecula tiene velocidad v antes de chocar e ímpetu mv después de la colisión, rebota y su ímpetu es m(-v) o sea -mv.

Es claro que como la colisión es elástica, el ímpetu inicial es igual al ímpetu después de la colisión. Por lo tanto, el cambio neto en el ímpetu de las partículas es +mv_x - (-mv_x) = 2mv_x; donde V_x, es la velocidad de la partícula medida a lo largo del eje x, como se muestra en la figura 6. El punto esencial del evento es que en un intervalo de tiempo antes y después de la colisión hay un cambio en el ímpetu de la molécula. Recordemos ahora que la segunda ley de Newton, que rige la dinámica de cuerpos en movimiento, nos dice que el cambio en el ímpetu de un móvil dado es igual a la fuerza actuando sobre él. ñPero en nuestro modelo no hay fuerzas a excepción de las producidas en las colisiones! Esto implica que la partícula, al chocar contra la pared, imprime sobre ésta una fuerza igual y opuesta a la que la pared ejerce sobre ella y de magnitud igual a 2mv_x. Hemos llegado a una conclusión extraordinaria: las moléculas al chocar contra una superficie ejercen una fuerza sobre ella. ñY la presión no es más que la fuerza ejercida por unidad de superficie! Es inevitable pues pensar que la presión sobre cualquier superficie, real o imaginaria, que se ponga en contacto con el gas va a provenir del efecto de las colisiones entre las moléculas del gas y dicha superficie. Esta conclusión es correcta; veamos ahora lo que ocurre.

Consideremos un intervalo de tiempo de un segundo, tiempo muy pequeño comparado con la duración de un experimento, pero muy grande comparado con la "vida" que tiene una molécula entre dos colisiones sucesivas. En un gas a 0ñ C y presión atmosférica, esta "vida media", conocida en la jerga cinética como tiempo libre medio, es del orden de 10^-10 seg: ñun décimo de nanosegundo! Esto quiere decir que en promedio cada molécula choca 10¹⁰ veces cada segundo. Y decimos en promedio porque es evidente que dada la naturaleza estadística de nuestro modelo sólo podemos hacer consideraciones que reflejen eso, el comportamiento promedio de las partículas. Imagínense entonces la cantidad de colisiones que ocurren sobre un área de un cm² de la pared. Si en un cm³ hay del orden del 10¹⁹ moléculas, con suponer que sólo una fracción pequeña de ellas, digamos 10 ¹⁰, choquen con ella, en un segundo tendremos en ese centímetro cuadrado (10¹⁰) x (10¹⁰) = 10²⁰ colisiones en un seg. ñLa presión ejercida pues no es despreciable! Y esto, en efecto, es lo que le ocurre a las partes sensoras de los instrumentos con que se mide la presión en gases: durante el intervalo de tiempo que dura la medición son bombardeados despiadadamente por las moléculas del gas, las cuales, por cada choque, transmiten un fuerza dada sobre tal superficie. Dicha fuerza, que resulta de estas colisiones, es lo que produce "la presión" del gas. Para aquellos lectores que estén más interesados en la materia, una deducción muy simple de la fórmula para esta presión está contenida en el Apéndice I.

Pero vayamos un poco más adelante y consideremos el comportamiento de un gas encerrado en una caja de volumen V, cuya superficie superior es un émbolo movible. Vamos a suponer que en este experimento mantenemos la temperatura del gas constante. Fijemos ahora el émbolo en una posición dada, como la mostrada en la figura 7(a) y 7(b). Sean V₁ el volumen y p₁ la presión del gas en estas condiciones. Si ahora desplazamos el pistón hasta ocupar la posición AB de la figura 7(b), el volumen V₂ es mayor que V₁. En este caso, el número de partículas por unidad de volumen será menor y por lo tanto, el número de colisiones por segundo entre ellas y cada cm₂ de la superficie del émbolo también. La transferencia de ímpetu, es decir la fuerza transmitida por los choques moleculares, también disminuirá y, consecuentemente, la presión p₂ será menor. Si regresamos el émbolo a su posición original AB, u otra que determine un volumen menor; la presión aumentará. De aquí vemos que el número de partículas por unidad de volumen varía al cambiar el volumen del recipiente. Por lo tanto, en un intervalo de tiempo fijo, digamos un segundo, el número de colisiones entre las moléculas y las paredes del recipiente, en particular con la pared del émbolo, también cambia. Consecuentemente la presión es mayor si el volumen es menor y viceversa. En todo este razonamiento hemos supuesto que la temperatura permanece constante. Simbólicamente:

pV = const. (si T es constante)

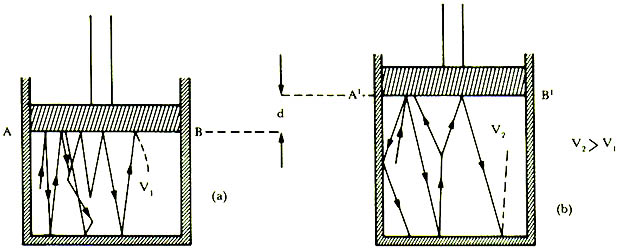
Figura 7. (a) El volumen ocupado por las moléculas v₁ es consistente con una cierta presión p₁ producida por los choques de las moléculas con la superficie del émbolo. En (b) al aumentar el volumen la presión disminuye como consecuencia de la disminución del número de choques moleculares.

Esta relación entre presión y volumen fue descubierta en el año de 1662 por el físico inglés Robert Boyle y hoy se conoce como la ley de Boyle. ñEsto es gratificante! Nuestro simple modelo no sólo nos sirve para comprender el significado de la presión de un gas en términos moleculares, sino que también hemos deducido a partir de él, y de manera muy simple, una de las relaciones más famosas que rigen el comportamiento de los gases. Curiosamente Newton en su magnífica obra Principia que data de 1687 ya hace notar que la ley de Boyle puede obtenerse si uno supone que entre los átomos que forman un gas existen fuerzas repulsivas que varían en forma inversamente proporcional a la distancia entre los átomos. En nuestro modelo estas fuerzas repulsivas son de hecho de valor infinito en el momento de la colisión y cero para distancias mayores al diámetro de la molécula. Por lo tanto, nuestro modelo se apega mucho más al propuesto por Bernoulli en 1738.

Robert Boyle

Rudolf Clausius

Pero todavía podemos aprender más sobre el comportamiento mecánico de un gas. Supongamos que en la figura 7 la transición del estado del gas representado en la parte (a) al estado del gas representado en la parte (b) es inducido por las colisiones mismas. Podemos pensar que sobre el émbolo en (a) tenemos un conjunto de pesas que al removerlas una a una permiten que el gas se expanda lentamente, como consecuencia de la presión ejercida por los choques moleculares, hasta llegar a (b).

Conceptualmente podemos pensar también que a lo largo de toda esta expansión indicada por la letra d en la figura 7, las colisiones moleculares ejercen una presión sobre la superficie del émbolo. Esta presión se manifiesta en la fuerza necesaria para desplazar el émbolo a lo largo de d. Al final del proceso, cuando éste se detiene en la posición A'B', se imprime una fuerza neta sobre él a lo largo de la distancia d. Si recordamos que el trabajo mecánico realizado por una fuerza actuando a lo largo de una distancia dada es proporcional al producto de dicha fuerza por la distancia, concluimos que los choques moleculares sobre el émbolo producen una cierta cantidad de trabajo mecánico. ñEn forma natural, el concepto de trabajo mecánico también surge de nuestro modelo! Y como dicho trabajo está relacionado con la energía, también se nos presenta otra interrogante muy pertinente: ¿de dónde proviene esta energía? Es evidente que ésta debe provenir de las partículas mismas, pues, como hemos insistido varias veces, no hay otra forma de energía involucrada en el sistema. Pero la única energía presente es la energía cinética de cada partícula, ya que también hemos eliminado del modelo cualquier forma de energía potencial proveniente de interacciones moleculares. Por lo tanto, la lógica nos dice que si el modelo es adecuado, en alguna forma debemos explicar cómo las diferentes formas de energía mecánica, y también el calor, están relacionadas entre sí. Para ello debemos retroceder un poco y recordar algunas características del modelo cinético. Si llamamos m a la masa de cada una de las moléculas y v a su velocidad, la única energía que podemos asociarle a cada molécula es su energía cinética, definida como (1/2) mv². El problema central ahora es que v² cambia continuamente debido a las colisiones moleculares, algo así como 10 ¹⁰ veces cada segundo. Tratar de llevar un registro de la energía cinética de una molécula es, como ya dijimos, una tarea monumental. Y qué decir de las energías cinéticas de N moléculas. De nuevo recurrimos a la hipótesis de que en ausencia de una forma efectiva de llevar tal registro y de la presencia de una enorme cantidad de moléculas en el gas, podemos pensar en valores promedio. Así pues, como el gas está en equilibrio podemos suponer que a cada molécula de manera individual le podemos asociar una energía cinética promedio, a la cual llamaremos . Más aún, como el gas está en equilibrio, la forma en que están distribuidos estos valores promedio sobre todas las moléculas del gas no cambia con el tiempo. Consecuentemente podemos definir la energía cinética total del gas como el número total de moléculas multiplicada por la energía cinética promedio de cada molécula**

A la luz de estos conceptos veamos qué ocurre en las experiencias mostradas en la figura 7, suponiendo ahora que las paredes del cilindro están aisladas de los alrededores para no permitir el intercambio de calor. Si nosotros aumentamos la presión del gas manteniendo el volumen constante, el número de choques entre las partículas del gas con las paredes aumenta y por lo mismo, también el número de colisiones entre las partículas mismas (ya que aun con respecto a una superficie imaginaria colocada dentro del gas, este aumento es perceptible). Al ser más frecuentes las colisiones, las velocidades también cambian en magnitud y dirección con más frecuencia, de manera que el promedio del cuadrado de la velocidad debe cambiar. Como el volumen es constante, debemos esperar que al aumentar la presión la energía cinética promedio aumente. El lector curioso o dudoso de este argumento puede ir al Apéndice 1 para cerciorarse que así es en efecto.

Lo esencial del argumento aquí expuesto es que si el número de moléculas N en el recipiente es constante, a mayor presión, mayor energía cinética promedio por cada molécula. Por lo tanto, una propiedad mecánica, como la presión, está correlacionada con una cantidad estrictamente molecular: la energía cinética promedio de las moléculas que forman el gas. Esto nos lleva a la primera respuesta de la pregunta planteada: si en un sistema adiabático (aislado) suministramos trabajo mecánico al sistema, éste se convierte en energía cinética, pues la energía cinética promedio por partícula aumenta. Esta aseveración constituye la interpretación microscópica de la primera ley de la termostática. Sin embargo, al hacer esta aseveración conviene subrayar vehementemente que esta interpretación ha surgido de la adopción de un modelo específico para describir las propiedades de un gas y por consiguiente su validez está circunscrita a sólo aquellos sistemas (gases) para los cuales sea justificable emplear este modelo. Por el contrario, las leyes de la termostática se aplican a cualquier sistema físico, independientemente*** de cuál el modelo microscópico sea útil para explicarlos.

Llegamos ahora al punto culminante de lo que espero sea una interesante discusión. ¿Cómo introducimos el concepto de calor al modelo? Esto nos llevará necesariamente a considerar la interpretación cinética de la temperatura. Note el lector que este problema es complicado. Las dos variables dinámicas relevantes en el sistema, es decir en el gas, son el ímpetu de las moléculas y su energía cinética promedio. El cambio en el ímpetu por choques moleculares está asociado con el concepto de presión. La energía cinética promedio también guarda a su vez una relación estrecha con la presión a través del resultado ya mencionado: a mayor presión, mayor energía cinética si N no varía. Este resultado es de hecho la síntesis de cómo están relacionadas entre sí propiedades mecánicas con propiedades microscópicas. Difícilmente pues podemos dar un paso más en esta dirección. La temperatura no tiene un origen mecánico, sino que proviene estrictamente de cuantificar las sensaciones de caliente y frío. ¿Estamos en un callejón sin salida? Veamos qué nos dice el experimento. Tomemos de nuevo un recipiente conteniendo gas como se muestra en cualquiera de las figuras 7 y consideremos qué le sucede a dicho gas si aumentamos o disminuimos su temperatura, por ejemplo, calentándolo con un mechero o enfriándolo con hielo, aunque manteniendo la presión constante. Si un gas se enfría continuamente desde 0ñ C, temperatura a la cual ocupa un cierto volumen V_o, manteniendo la presión constante, por cada grado que disminuya la temperatura, su volumen disminuye en de V_o. Recíprocamente el volumen aumenta con la temperatura a presión constante. Estas experiencias llevadas a cabo por los físicos franceses J. A. Charles y J Gay-Lussac se conocen como la Ley de Charles. Ahora bien, de acuerdo con nuestro modelo, si la presión es constante y el volumen disminuye, lo único que según los argumentos anteriores puede disminuir es ; la energía cinética media de las moléculas. Y recíprocamente, si el volumen aumenta a presión constante, dicha energía debe aumentar. Así pues, si queremos conciliar nuestro modelo con el experimento, suponemos que la energía cinética media de las moléculas sea una "medida" de la temperatura del sistema. Propongamos entonces como una hipótesis adicional que tal energía sea proporcional a T. Una vez aceptado esto, la constante de proporcionalidad es muy fácil de determinar; pero esto lo dejaremos para el Apéndice 2. Lo importante aquí es reconocer que éste es uno de los resultados más impactantes de toda esta discusión. La interpretación de la temperatura como una medida de la "agitación molecular", entendida ésta como la magnitud de la energía cinética promedio por partícula, marca la pauta final para llegar al clímax de esta discusión: no sólo podemos ahora entender desde el punto de vista microscópico que los conceptos de calor y trabajo son diferentes manifestaciones de una forma de energía, sino que además hemos podido conciliar los aspectos estrictamente mecanicistas de nuestro modelo, sintetizados en dos resultados:

a) la presión ejercida por las colisiones moleculares en un gas es proporcional a la energía cinética promedio del gas.

b) la temperatura de un gas es proporcional a la energía cinética total del gas tomada como la suma de la energía cinética promedio de cada una de las moléculas que lo componen.

Las otras propiedades de equilibrio inherentes al modelo emanan de él en forma natural. Veamos cada una de estas cuestiones individualmente.

Tomemos la pregunta acerca de cómo introducimos el calor al modelo. La respuesta es ahora trivial. Si calentamos el gas, aumentamos la agitación molecular, esto es, aumentamos la energía cinética promedio; si lo enfriamos, dicha energía disminuye. Pero lo mismo ocurre si realizamos trabajo mecánico sobre el gas, o si éste lo cede a los alrededores. Lo que en física macroscópica no podemos distinguir por presentársenos el sistema como una caja negra, el acceso a éste en el caso de un gas devela el misterio: calor y trabajo no son más que diferentes manifestaciones del grado de agitación molecular que el sistema exhibe bajo diferentes circunstancias. Y la cuantificación de este grado de agitación se obtiene, de acuerdo con nuestra hipótesis adicional, a través de la temperatura.

Respecto a las otras propiedades de equilibrio, sólo nos referiremos a las más importantes. Empecemos con la energía interna: ya vimos que en el modelo adoptado la energía total del sistema es igual a la energía cinética promedio de cada molécula multiplicada por el número de moléculas. Además, de acuerdo con la interpretación cinética que le hemos dado a la temperatura, ambas son proporcionales entre sí. Como ésta es la única forma de energía inherente al modelo mismo, ñes lógico asociarla con la energía interna de la termostática! De nuevo, en la termostática nos está vetado el acceso a la estructura del sistema y sólo podemos establecer una definición operacional de la misma. Aquí la única energía que se afecta al realizar trabajo mecánico es, como ya vimos antes, la energía promedio total; por lo tanto, la asociación de esta energía con la energía interna ocurre de manera natural. En resumen podemos decir que para nuestro modelo, su energía interna es también proporcional a la temperatura. Por otra parte, la capacidad calorífica se define como el cociente entre incremento en esta energía debido a un aumento en la temperatura. Esto implica que la capacidad calorífica es constante. Para un mol de gas se puede demostrar que esa constante es igual a (3/2)R, donde R es la constante universal de los gases. El lector interesado puede ver el Apéndice 3 para una demostración elemental de esta afirmación. Este resultado concuerda maravillosamente bien con los resultados experimentales obtenidos para los gases nobles Ar, Kr, Ra y Xe. Como la ecuación de estado para estos gases también corresponde a la ecuación gas ideal, esto es, la ecuación de Boyle, podemos concluir que el modelo que hemos propuesto es adecuado para entender cómo se comportan los gases ideales desde el punto de vista microscópico. Nuestro modelo corresponde, pues, al de un gas ideal.

A manera de tener una idea cualitativa de cómo el modelo cinético del gas ideal genera otros resultados comparables con el experimento, consideremos la velocidad del sonido en gas. Esta velocidad resulta de perturbar un gas en equilibrio de manera que la perturbación produzca una variación en su densidad, enriqueciéndose ésta en ciertas regiones del gas y empobreciéndose en otras. La forma en que se repiten las zonas enriquecidas y empobrecidas corresponden a la de una onda que se propaga con una cierta velocidad que es precisamente la del sonido. Y esta velocidad puede medirse con bastante precisión en el laboratorio. En nuestro modelo, el promedio del cuadrado de la velocidad de las moléculas es, como acabamos de indicar, proporcional a la temperatura del gas. Así pues, la raíz cuadrada de esta cantidad corresponde a una velocidad característica de sus moléculas. Si calculamos ésta y la comparamos con la velocidad del sonido de algunos gases simples, obtenemos los resultados mostrados en la tabla 1. El cálculo de está esbozado en el Apéndice 3. Aunque la concordancia no es del todo satisfactoria, vemos que para los dos primeros gases ambas velocidades son del mismo orden de magnitud.

Vale la pena mencionar que la propia teoría cinética de los gases da lugar a una fórmula más precisa para la velocidad del sonido en gases monatómicos. Los valores numéricos que se extraen de dicha fórmula concuerdan satisfactoriamente con los obtenidos experimentalmente.

TABLA I.- La velocidad del sonido en algunos gases se comparan con Vrpc = . Para los tres primeros gases la concordancia es notable:

Gas	Vipc en m/seg	Vel. sonido en m/seg	Peso molecular (M)
Ar	412.5	331.45	39.948
Ne	584	435	20.17
He	1.311	965	4.002
CO	493	338	28.01
N2 ñ	493	334	28.01
O2 ñ	461	316	32

Como una última aplicación de los resultados obtenidos con nuestro modelo cinético de un gas ideal, mencionaremos un problema que a primera vista parecería alarmante. Todos sabemos que el planeta Tierra está rodeado de una capa atmosférica constituida fundamentalmente de una mezcla de gases, en la cual el más abundante es el aire. Debido a la fuerza de atracción gravitacional que la Tierra ejerce sobre dichos gases, la densidad de la atmósfera es mayor cerca de la superficie terrestre. A medida que nos alejamos de ella, no sólo la densidad disminuye, sino que la temperatura aumenta. Esto tiene dos consecuencias inmediatas: la primera es que como el número de partículas por unidad de volumen decrece, el número de colisiones también disminuye, y por lo tanto la "vida media" o tiempo libre medio de cada molécula es mayor. A 1 000 kilómetros de altura este tiempo puede ser hasta de una décima de segundo el cual comparado con los nanosegundos de vida en un gas en condiciones normales, es enorme. Si pensamos que la molécula viaja aproximadamente a 300 m/seg, esto implica que la partícula puede recorrer del orden de 3 km ñantes de chocar con otra! Si además la molécula está alejándose de la Tierra y su velocidad al iniciar su viaje después de su última colisión es mayor de 10 km/seg, podrá salir disparada de la atmósfera sin que la fuerza de atracción ejercida por la Tierra pueda hacer nada por retenerla. Esto nos lleva a la segunda consecuencia, a saber, preguntar qué tan factible es que haya moléculas que tengan velocidades tan altas en las capas superiores de la atmósfera. La relación de proporcionalidad propuesta entre la energía cinética media de las moléculas y la temperatura nos da la respuesta. En efecto, esta energía depende sólo de la temperatura, la cual en dichas capas de la atmósfera puede llegar a ser hasta de 1 300ñK. ñLa proporción de moléculas con velocidades altas es mayor! Más aún, como el promedio del cuadrado de la velocidad es inversamente proporcional a la ma sa de las moléculas, entre menor sea su masa, ñmayor será ! Estos argumentos nos llevan a pensar que la atmósfera de la Tierra y, de hecho, de cualquier planeta o sus satélites pierden sistemáticamente moléculas, de preferencia ligeras, de sus atmósferas. ¿Nos quedaremos sin aire algún día? Afortunadamente la rapidez con que este fenómeno ocurre es muy lento: una molécula de hidrógeno, la más ligera de todas, tarda como 1 000 años en escapar a partir de que es liberada de la atmósfera por algún mecanismo. Posiblemente la contaminación sea más efectiva en deteriorarla que este proceso. Pero en la Luna y otros planetas pequeños este proceso desempeñó un papel importante en la pérdida de sus atmósferas.

NOTAS

* Para mayores detalles, consultar la referencia (2) de las lecturas sugeridas.

**

*** Ver referencia (2) para mayores detalles