V. LA DISTRIBUCIÓN DE VELOCIDADES EN UN GAS
UNA de las características más sobresalientes de nuestro modelo
cinético es la concerniente a la forma en que hemos concebido con qué velocidad,
en magnitud y dirección, se mueven las moléculas que forman el gas. Así como
a priori no hay números privilegiados en los billetes de lotería, de la misma
manera no hay direcciones privilegiadas para las velocidades; además, la magnitud
de la velocidad puede variar desde cero hasta una velocidad máxima. Esto nos
lleva a pensar en caracterizar a las moléculas por su velocidad promedio, dada
la imposibilidad de observar en lapsos sucesivos cómo varía individualmente
la velocidad en magnitud. Y hasta el momento nos hemos encontrado ya con dos
promedios: el de la velocidad misma y el del cuadrado de la velocidad, el cual
apareció cuando discutimos el concepto de energía cinética promedio por molécula.
¿Cómo distinguimos entre esos dos promedios? Veamos un ejemplo muy simple. Imaginemos
que el gas consiste de 10 partículas que en un momento dado tienen velocidades
de 1 m/seg, 2 m/seg, 3 m/seg, 4 m/seg, 5 m/seg hasta 10 m/seg, respectivamente.
La velocidad "promedio" de cada partícula la calculamos en la misma forma que
sacamos nuestro "promedio" de calificaciones en un periodo escolar: sumamos
todos los valores y dividimos entre el número total de ellas.
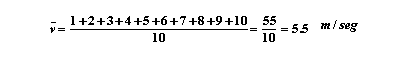
Por lo tanto, la velocidad promedio de cada molécula es de 5.5 m/seg en ese instante. Por un razonamiento análogo podemos calcular el promedio del cuadrado de la velocidad, que estará dado por
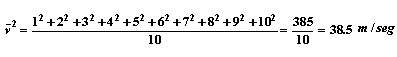
y por lo tanto la raíz cuadrada de 
será
de
=
6.21 m/seg
que es casi igual a 
Sin
embargo, observemos que es
mayor que 
. Y
recordemos también que
es la velocidad que en forma natural aparece asociada con la temperatura del
gas.
¿Cómo se comparan la velocidad promedio
y la raíz cuadrada del valor promedio del cuadrado de la velocidad,
, en nuéstro gas formado por 1023 partículas? ¿Son más o menos iguales?
¿Essiempre
mayor que ?
¿Existe otra velocidad característica como, por ejemplo, una velocidad máxima?
Y finalmente, ¿cuántas moléculas por unidad de volumen tienen una velocidad
,
en un intervalo dado, digamos entre l00 y 110 m/seg, en un instante dado? Si
pudiésemos responder estas preguntas aprenderíamos mucho. En efecto, si suponemos,
como lo hemos hecho hasta ahora, que el gas está en equilibrio, la forma en
que todos los posibles valores de la velocidad están "repartidos" en las moléculas
no va a cambiar con el tiempo; sólo son diferentes moléculas las que a tiempos
diferentes tienen también velocidades distintas. Y si conocemos esta repartición
podemos calcular, como en el ejemplo anterior; tanto
como .
Si recordamos, en ese ejemplo la distribución o repartición de velocidades fue
muy sencilla: a cada molécula le asignamos arbitrariamente un valor; pero, dado
a que la distribución de valores de 1 m/seg a 10 m/seg no cambiaba, no dijimos
a qué molécula le correspondía un valor determinado en cada instante.
Sin hacer ningún tipo de ejercicio matemático, el lector puede adivinar por
sí mismo cómo puede ser, cualitativamente, la forma de esta distribución o reparto
de velocidades. Grafiquemos en un sistema de coordenadas cartesianas el número
de partículas por unidad de volumen, digamos por cm3, que tienen
velocidades comprendidas en un cierto intervalo de velocidades; llamémosle Du,
contra la velocidad u. A este número le llamamos
N(u)Du.
¿Cómo varía este número con respecto a la velocidad u?
Relativamente fácil. Comencemos por el origen. ¿Cuál es el número de partículas
por unidad de volumen que tiene velocidad igual a 0 m/seg? Debemos sospechar
que es cero. En nuestra caja es muy difícil imaginar que entre todas las colisiones
violentas que ocurren y el incesante bombardeo a que está sometida cada molécula
alguna de ellas pueda estar en reposo. Aceptemos esta sospecha como un juicio
válido. La curva comienza pues en el origen de coordenadas en la figura 8. Y
como obviamente la velocidad u no puede ser
mayor que la velocidad de la luz, el número de partículas por unidad de volumen
con velocidades mayores que dicha velocidad es cero. Podemos inferir entonces
que la curva debe ser cero cuando la velocidad es muy grande. Así pues, la curva
empieza en cero y termina en cero. Si aceptamos además la existencia de una
velocidad máxima y pensamos en que es una curva que varía lisa y suavemente,
la opción más simple consecuente con estas hipótesis es que la curva tenga la
forma de una campana. Pero recordemos que este resultado es una mera conjetura
extraída de algunas consideraciones de lógica elemental y de un par de datos
objetivos acerca del comportamiento de las moléculas. ¿Podemos comprobar de
manera contundente si nuestra imaginación concuerda con el mundo real?
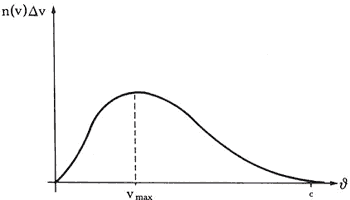
Figura 8. La forma cualitativa de la curva de la distribución de velocidades
en el modelo cinético.
Recurramos al experimento. ¿Cómo podemos medir la distribución de velocidades
en un gas a una temperatura y presión dadas? Si pensamos en un gas cualquiera
que éste sea, encerrado en un recipiente, no se ve en que forma más
o menos simple podemos introducir un selector de velocidades que nos vaya separando
las moléculas por grupos de acuerdo a la velocidad que tengan. Sin contar que
ese selector interferiría con el movimiento de las moléculas y seguramente modificaría
sus velocidades, lo cual no queremos que ocurra. Pero la naturaleza es generosa
y nos ha proporcionado de todos los elementos necesarios para llevar a cabo
esta medición. Veamos: lo primero que necesitamos es un conjunto de moléculas
(o átomos) muy grande que tengan velocidades cuya magnitud y dirección estén
distribuidos al azar. Es bien sabido que algunos metales, como el talio, la
plata, el litio y otros, al ser calentados a cierta temperatura emiten átomos
que tienen precisamente esa característica: sus velocidades son arbitrarias.
La emisión de estos átomos puede visualizarse como disparos de una superametralladora
de enorme ráfaga de balas por segundo, cada bala poseyendo una velocidad en
magnitud y dirección totalmente arbitraria; esto es, la N-ésima bala
tiene una velocidad que para nada depende de la que fue disparada antes que
ella, ni influye en la que le sigue. Ahora bien, el problema es cómo seleccionamos
balas distinguiéndolas por las velocidades que poseen. Esto es relativamente
fácil de resolver, imagine el lector que, de todas las moléculas o átomos emitidas
nos fijamos en aquellas que puedan salir por una rendija colocada a cierta distancia
del metal emisor y que sirve de colimador. Este colimador permite el paso solamente
a un grupo selecto de moléculas cuya velocidad en magnitud es arbitraria, pero
cuya dirección está determinada por la orientación que le demos a la rendija
respecto del emisor. Para distinguir entre las partículas que pasan por el colimador;
dado que las velocidades están distribuidas en magnitud, usamos un dispositivo
muy ingenioso. Imaginemos una rueda dentada cuyas ranuras están uniformemente
espaciadas a lo largo de su circunferencia. Si esta rueda está montada sobre
un eje giratorio conectado a un motor podemos hacerla girar con una velocidad
angular determinada. Cada ranura pasará por un punto fijo en el espacio a tiempos
bien determinados. Si conocemos la distancia entre la rueda giratoria y la rendija
podemos conocer el tiempo que le toma a un átomo de velocidad v
en viajar esa distancia (t = d/v); por lo tanto, para una velocidad
dada podemos contar las partículas que pasan por los dientes de la rueda por
medio de un detector. De esta manera podemos determinar el número de partículas
con velocidad v que pasan por ella y graficar ese número contra
v . Variando la velocidad angular de la rueda, seleccionamos
moléculas de diferente velocidad y así tenemos un selector de velocidades. Si
todas las moléculas (o átomos) emitidas por el filamento tuvieran la misma velocidad,
sólo detectaríamos por medio del detector los impactos causados para una sola
velocidad angular w. Pero no ocurre
así (Figura 9). Los datos experimentales obtenidos por el físico alemán Otto
Stern en 1920 y subsecuentemente mejorados hasta alcanzar una gran precisión
por Miller y Kusch en 1955 se muestran en la figura 10.
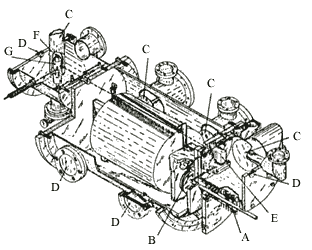
Figura 9. Esquema del aparato usado por Miller y Kush para determinar la distribución
de velocidades de Maxwell [Tomado del artículo de R. C.Miller y P. Kusch Physical
Review, vol. 99 p. 1314 (1955).]
Figura 10. La línea sólida muestra la distribución teórica de velocidades calculada
con la fórmula de Maxwell. Los círculos y/o triángulos D son los puntos experimentales
para átomos de talio que salen del horno a 870ñK y a 944ñK, respectivamente.
La abscisa se eligió en unidades adimensionales para que distribuciones de velocidades
a diferentes temperaturas incidieran sobre la misma curva. [Datos extraídos
del artículo de R. C. Miller y P. Kush, Physical Review, vol. 99, p.1314
(1955).] La ecuación de Maxwell-Boltzmann es:N(v)dv = 4
Pn(m/2Pht) e-mvñ2/2 htv2dv
En ella se ve claramente que la distribución es una curva en forma de campana
tal y como lo habíamos sospechado. En efecto, la curva exhibe las características
previstas: indica que el número de partículas con velocidad cero es cero y que
al crecer v la curva también tiende a cero. Nuestra intuición ha sido
gratamente corroborada. Y fue el gran físico escocés James Clerk Maxwell (*)
quien en 1860 dedujo la forma matemática de esta curva usando exdusivamente
la hipótesis número cinco del modelo cinético que hemos introducido. Si recuerdan,
esta hipótesis sólo establece el carácter estrictamente probabilístico de la
distribución de las velocidades de las partículas que forman el gas. Más tarde,
esa misma ecuación fue obtenida por otro gran científico, el austriaco Ludwig
Boltzmann (*), usando métodos más sofisticados. Boltzmann, conjuntamente con
Maxwell, pueden considerarse como los dos grandes precursores de la teoría cinética
moderna. Esta ecuación se conoce ahora como distribución de Maxwell-Boltzmann.
James Clerk Maxwell
Luis Boltzmann
Así llegamos a una feliz conclusión: nuestro modelo cinético no sólo conduce a resultados que son comprobables a posteriori con el experimento, sino que el postulado más importante en que está basado puede comprobarse directamente por los métodos arriba descritos. Como comentario final debemos insistir en que la validez de este modelo está circunscrita a describir correctamente las propiedades termostáticas de lo que llamamos un gas ideal. En la práctica estos gases, que en realidad no existen, se encuentran representados en los gases monatómicos a densidades bajas, o bien por los mismos gases a temperaturas altas, temperaturas mayores que la temperatura del punto crítico del gas. A densidades altas, el modelo falla; en estas condiciones la ley de distribución de velocidades de Maxwell-Boltzmann no es correcta y la teoría cinética de los gases debe corregirse esencialmente debido a que entre los átomos o moléculas que componen el gas existen fuerzas atractivas y repulsivas que no hemos tomado en cuenta aquí. Volveremos a este punto más adelante.
