II. EL MAGNETISMO Y LA LUZ (DESCRIPCI�N MACROSC�PICA)
EN ESTE cap�tulo deseamos presentar un panorama a vuelo de p�jaro
de los aspectos macrosc�picos del magnetismo. Los cient�ficos entienden que
la forma macrosc�pica de describir un fen�meno cualquiera es hallar una ley
que re�na en un postulado simple una serie de observaciones que el experimentador
ha realizado de manera sistem�tica. Estas observaciones s�lo involucran variables
macrosc�picas o fenomenol�gicas, que son las que se pueden definir operacionalmente,
y sus relaciones. N�tese que en la descripci�n macrosc�pica no se hace referencia
a ning�n modelo o mecanismo microsc�pico m�s fundamental. La ley fenomenol�gica
permite predecir nuevos fen�menos que, si son observados experimentalmente,
har�n que la misma sea validada. Sin embargo, las relaciones entre las variables
se obtienen por medio del experimento y no se deducen de la teor�a.
El electromagnetismo cl�sico es un ejemplo claro de teor�a macrosc�pica, y
logr� su formulaci�n final junto con la termodin�mica del siglo XIX.
Espec�ficamente, en este cap�tulo veremos c�mo una serie de observaciones realizadas
a partir del siglo XVIII condujeron a la formulaci�n de ciertas
leyes generales.
Como vimos en el bosquejo hist�rico, diversos cient�ficos lograron explicar y predecir nuevos fen�menos con estas leyes; as�, con el paso del tiempo, y gracias al genio de Faraday y sobre todo al de Maxwell, se logr� una s�ntesis maravillosa que dio pie al nacimiento de la teor�a electromagn�tica. Esta s�ntesis, a su vez, estimul� la formulaci�n de nuevos experimentos que desembocaron en los experimentos de Hertz y en las maravillosas tecnolog�as de nuestro siglo. Al mismo tiempo, y desde un punto de vista cient�fico, tres ramas de la ciencia: electricidad, magnetismo y �ptica, quedaron reunidas en un esquema conceptual poderoso que llev� al joven Einstein a crear su teor�a de la relatividad especial.
El lector curioso se habr� preguntado por qu� las leyes macrosc�picas tienen determinada forma y no otra. Junto con esta pregunta se plantea otra �ntimamente relacionada con ella y que tiene que ver con un punto fundamental. Es verdad que las leyes macrosc�picas nos proporcionan las relaciones entre las cantidades f�sicas. Tal y como lo mencionamos anteriormente, estas cantidades deben ser determinadas experimentalmente o por otro m�todo. La pregunta a que nos referimos est� relacionada con c�mo se pueden calcular estas cantidades f�sicas a partir de modelos microsc�picos o, como dicen los f�sicos, "a partir de primeros principios". N�tese que aqu� interviene una descripci�n a nivel at�mico o subat�mico que debe, al menos �sa es la esperanza, fundamentar las leyes macrosc�picas y las relaciones constitutivas (en el sentido de definici�n) que gobiernan las cantidades f�sicas que tienen una realidad experimental tangible.
Hechas estas aclaraciones, procederemos a describir las leyes fundamentales del electromagnetismo, as� como la s�ntesis realizada por Maxwell, y de all� pasaremos a describir c�mo estas leyes permitieron la explicaci�n del fen�meno luminoso y de otros muchos fen�menos relacionados con �l. Para esto haremos hincapi� en los conceptos de campo, materia y radiaci�n, ya que �stos forman la base de la descripci�n de los fen�menos electromagn�ticos. Por supuesto, pondremos un �nfasis especial en la parte magn�tica, as� como en el estudio de materiales magnetizados.
Un �ltimo comentario puede serle �til al lector. Como describimos en el cap�tulo
I, el hombre empez� a notar que ciertos materiales como la magnetita ten�an
propiedades que ahora llamamos magn�ticas. Antes de la revoluci�n cient�fica,
el estudio de estos materiales ya hab�a atra�do la atenci�n de los cient�ficos.
A partir del siglo XIII y culminando en la obra de Faraday y Maxwell,
se desarroll� el concepto de campo magn�tico (y el�ctrico) que demostr� ser
fundamental para el avance del electromagnetismo y condujo a demostrar que la
radiaci�n luminosa no era sino una onda electromagn�tica. Esto permiti� atacar
un sinn�mero de problemas, lo que llev� a su vez a la explosi�n que estamos
viviendo acerca del estudio de materiales magnetizados y de los diversos tipos
de magnetismo que se encuentran en la naturaleza. Finalmente, con la mec�nica
cu�ntica se pudo dar una base m�s fundamental y macrosc�pica a los conceptos
de campo, magnetizaci�n, etc�tera.
Podr� parecer al principio de nuestra exposici�n que el concepto de campo tiene poca relaci�n con el magnetismo en los materiales, pero �sta ser� una impresi�n falsa, pues, como veremos m�s adelante, la formulaci�n de la idea de campo y la comprensi�n de las leyes de Maxwell, de hecho, facilitan el entendimiento de por qu� los materiales magn�ticos se comportan como lo hacen.
LOS CAMPOS MAGN�TICO Y EL�CTRICO
Las ecuaciones de Maxwell unifican la teor�a electromagn�tica en forma elegante y compacta. En la figura 10 se presenta su forma diferencial, que aparece en notaci�n vectorial. No crea el lector que a continuaci�n procederemos a utilizar tan formidable representaci�n matem�tica y que los no iniciados perder�n el hilo de la materia. Solamente queremos mostrar c�mo lucen estas ecuaciones antes de introducir el concepto de campo. Como se ve, en ellas aparecen dos cantidades f�sicas, E y B, que son el campo el�ctrico y el magn�tico respectivamente. Esto nos indica que las ecuaciones de Maxwell se ocupan de c�mo los campos est�n relacionados entre s� y nos lleva a caer en la cuenta de que el concepto de campo es esencial para interpretar y describir cualquier fen�meno electromagn�tico.
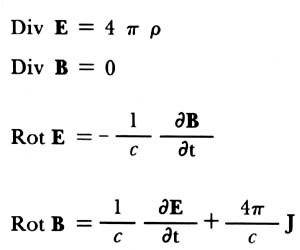
Figura 10. Ecuaciones de Maxwell en el vac�o.
Faraday introdujo el campo el�ctrico, el cual describiremos brevemente antes
de estudiar el campo magn�tico. Supongamos que se tiene un arreglo de cargas
fijas en el espacio y que estamos interesados en el efecto que �stas tienen
sobre otra carga q que se lleva a su vecindad. La distribuci�n de carga
ejerce una fuerza sobre q proporcional a la misma carga q. El
campo el�ctrico E asociado a esta distribuci�n de cargas es esta misma
fuerza dividida entre q. Esto se hace para obtener una cantidad que solamente
depende de la distribuci�n de cargas original. Ahora bien, para aclarar m�s
esta definici�n del campo recordemos que en el siglo XIX el efecto
de una carga sobre otra parec�a ocurrir instant�neamente; de all� se deriv�
el concepto de "acci�n a distancia", esto es, que al tener una configuraci�n
de cargas y al mover, digamos, una de ellas, resulta que las otras parecen sentir
su acci�n de inmediato, no importando a qu� distancia se encuentre la carga.
A Faraday se le ocurri� visualizar el campo en t�rminos de l�neas de campo.
�stas son curvas cuya tangente, en cualquier punto, tiene la misma direcci�n
que la fuerza entre las cargas.
Estas curvas son continuas, excepto donde hay cargas o el campo es cero. Mientras
m�s densas sean estas l�neas de campo, m�s fuerte es el mismo. N�tese que el
campo el�ctrico (y el magn�tico) son cantidades que poseen magnitud y direcci�n,
o sea que para definirlas necesitamos de estos dos datos. En lenguaje matem�tico,
los campos son vectores. En la figura 11 se muestran algunas l�neas de campo
cuando interact�an una carga positiva de + 3 unidades y otra negativa de 1 unidad.
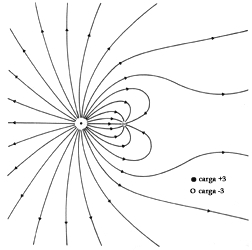
Figura 11. Algunas l�neas de campo del campo el�ctrico de dos cargas q1 = +3, q2 = -1.
Como se observa, el campo es muy grande cerca de las cargas y las l�neas se vuelven menos densas conforme nos alejamos de ellas. Las flechas indican que si ponemos una carga positiva q de prueba de una unidad, �sta ser� atra�da por la carga negativa si la ponemos entre las dos cargas y repelida radialmente por la carga positiva si q est� en el segundo y tercer cuadrante. Si q est� en el primero y cuarto cuadrante, ser� repelida de otra manera.
Ahora bien, �c�mo definimos el campo magn�tico? �ste es m�s dif�cil de definir que el el�ctrico por la siguiente raz�n: tal y como se nota en la segunda ecuaci�n de la figura 10, existe una asimetr�a entre el campo el�ctrico y el magn�tico debido a que no hay cargas magn�ticas aisladas. Esto implica que la situaci�n descrita anteriormente no es aplicable al caso magn�tico, pues las l�neas de campo no pueden salir o llegar a las cargas magn�ticas aisladas ya que simplemente no existen.
Si bien podemos colocar dos imanes con sus polos norte y sur y trazar l�neas de campo entre ellos, una definici�n m�s consistente debe estar ligada al movimiento de una carga. Esto es esencial: el magnetismo, aun cuando empez� a estudiarse desde tiempos remotos, no fue incorporado dentro de un esquema conceptual m�s vasto ni se empez� a estudiar en forma din�mica hasta el descubrimiento de Oersted en 1820.
De la misma manera en que definimos el campo el�ctrico como la fuerza que se ejerce sobre una carga unitaria en reposo, podemos definir otro campo, el magn�tico, como la parte de la fuerza que involucra la velocidad de la carga y act�a sobre una carga en movimiento. Por lo tanto, la fuerza que act�a sobre una carga tiene una parte est�tica que sirve para definir el campo el�ctrico y una parte din�mica que lo hace para el campo magn�tico. Esta es la conocida fuerza de Lorentz, llamada as� en honor del gran f�sico holand�s de este nombre.
Con el campo definido de esta manera se puede predecir la parte dependiente de la velocidad para la fuerza que act�a sobre cualquier part�cula cargada movi�ndose a una velocidad dada. El concepto de campo es muy poderoso, pues conociendo el campo el�ctrico y el magn�tico en un punto podemos predecir el movimiento de cualquier carga en este punto.
�Son reales estos campos? Para cient�ficos como Faraday y Maxwell los campos ten�an una realidad f�sica incontrovertible. Sin embargo, esta pregunta que en la actualidad recibe una gran atenci�n no tiene una respuesta f�cil. Creamos, pues, en la realidad de los campos, olvidando la "acci�n a distancia", y usemos esta poderosa representaci�n para penetrar en el misterio de la luz y los materiales magn�ticos. El describir los fen�menos electromagn�ticos en t�rminos de campos permite que el fundamental concepto de energ�a pueda ser introducido en forma natural. Los campos son portadores de energ�a. De hecho, es frecuente mencionar que tanto el campo el�ctrico como el magn�tico almacenan energ�a. Dada una distribuci�n de cargas o corrientes el�ctricas, se tiene una energ�a potencial asociada a la misma. M�s espec�ficamente, dado un campo, la energ�a potencial asociada al mismo se representa como el cuadrado del campo en cuesti�n. Al describir la propagaci�n de ondas electromagn�ticas veremos que es natural asociar la energ�a que transportan las ondas con la energ�a de los campos.
Las leyes de Maxwell resumen y encuadran dentro de una teor�a poderos�sima los conocimientos que sobre el comportamiento de los campos, cargas y corrientes en el vac�o y en la materia se hab�an venido acumulando durante muchos a�os de investigaci�n. Su formulaci�n matem�tica luce imponente (Figura 10), pero el lector interesado en el magnetismo puede, con un poco de esfuerzo, penetrar en el significado f�sico que contienen estas leyes.
A continuaci�n describiremos las leyes fundamentales del electromagnetismo y su relaci�n con los fen�menos fundamentales en la materia. Aun cuando este libro se ocupa del magnetismo, describiremos brevemente las leyes que versan sobre las cargas y corrientes el�ctricas pues, como hemos visto, las cargas magn�ticas libres o monopolos magn�ticos no existen y son estas corrientes el�ctricas las que generan campos magn�ticos en el vac�o. Estos campos son de la misma naturaleza que el campo magn�tico producido por un im�n por medio de un mecanismo microsc�pico, por lo que el estudio de las leyes de Maxwell nos ser� de mucha utilidad para discusiones posteriores.
Cuatro son las leyes de Maxwell. �stas, de hecho, fueron descubiertas por cient�ficos anteriores a este gran f�sico. Sin embargo, �ste supo reformularlas, completarlas y obtener de ellas un torrente de informaci�n sobre los fen�menos electromagn�ticos.
1) Ley de Gauss, que se ocupa del campo y de las cargas el�ctricas y es equivalente a la famosa ley de Coulomb;
2) Ley sobre la ausencia de cargas magn�ticas libres;
3) Ley de Faraday, sobre la inducci�n electromagn�tica, y
4) Ley de Ampère-Maxwell sobre la dependencia del campo magn�tico de la corriente el�ctrica y la variaci�n del campo el�ctrico.
Hay que enfatizar que estas leyes fueron descubiertas experimentalmente; con excepci�n de una parte de la ley de Ampère-Maxwell (la parte de Maxwell). Se puede afirmar que fue Faraday quien, al descubrir la ley que lleva su nombre, introdujo el campo magn�tico en 1845. Junto con estas leyes existen las llamadas relaciones constitutivas, que relacionan los campos con la magnetizaci�n y polarizaci�n de la materia. Estas relaciones y la fuerza de Lorentz, descrita anteriormente, completa el gran edificio del electromagnetismo cl�sico. Pasemos a recorrerlo en detalle para adquirir un conocimiento m�s completo de su estructura.
La ley de Gauss es equivalente a la ley de Coulomb, la cual asevera que la fuerza entre dos cargas es inversamente proporcional al cuadrado de la distancia que las separa. Dicha fuerza puede ser repulsiva o atractiva, seg�n que las cargas sean de signo igual o contrario respectivamente. Esta ley ha sido comprobada emp�ricamente en innumerables ocasiones. Como vimos m�s atr�s, el campo el�ctrico est� relacionado con la fuerza entre una carga de prueba y otra carga, ya que si dividimos esta fuerza entre la carga de prueba obtenemos el campo el�ctrico producido por la otra carga. Es notable que la fuerza con la cual interact�an dos cargas no cambia por la presencia de una tercera.
As� pues, el campo el�ctrico es producido siempre por una fuente, la cual puede ser una carga o un sistema de cargas. La relaci�n entre el campo el�ctrico y sus fuentes puede ser expresada en forma sencilla definiendo el concepto de flujo. En la figura 12 se representa una superficie cerrada de forma arbitraria. El campo representado por las l�neas atraviesa esta superficie. Si la dividimos en peque�as secciones de tal forma que cada pedazo de superficie sea plano y el campo el�ctrico no cambie apreciablemente de una secci�n a la contigua, podemos definir el flujo como el producto del campo el�ctrico por el �rea de la secci�n que atraviesa. O sea que el flujo nos da una idea de qu� tanto campo atraviesa una superficie si usamos todas las secciones que componen esta superficie.
Hasta ahora hemos considerado que la superficie no encierra ninguna carga. Pero �qu� ocurre si lo hace? Es la ley de Gauss la que nos da la respuesta: el flujo de campo el�ctrico a trav�s de cualquier superficie cerrada es proporcional a la carga total encerrada por esa superficie. Esta es una ley que tiene el mismo contenido f�sico que la ley de Coulomb, pero expresado en t�rminos del campo y no de la fuerza. Asimismo permite la obtenci�n de expresiones para el campo electrost�tico dado cualquier arreglo de cargas en reposo. De hecho, el campo el�ctrico decrece de la misma forma que el cuadrado de la distancia al alejarse de una carga puntual.
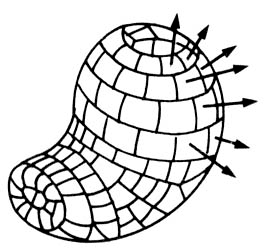
Figura 12. Una superficie cerrada sobre un campo se divide en peque�os elementos de �rea. Cada elemento se representa por un vector.
Muchas veces, sin embargo, la cantidad que se utiliza para obtener informaci�n
acerca del campo el�ctrico es la diferencia de potencial que aparecer� tambi�n
al examinar la ley de inducci�n. El potencial el�ctrico es una cantidad escalar,
pues s�lo se describe con una magnitud, y sirve para medir la cantidad de trabajo
por unidad de carga que se realiza al mover una carga positiva de un punto a
a un punto b en el campo el�ctrico (Figura 13).
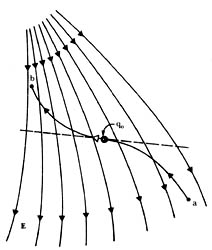
Figura 13. Una carga de prueba q0 se mueve de a a b en un campo el�ctrico por medio de la acci�n de una fuerza externa.
La diferencia de potencial entre los dos puntos es independiente de la trayectoria que se tome para ir de a a b y su variaci�n nos proporciona el campo el�ctrico. Para hacer contacto con las manifestaciones cotidianas de la electricidad, diremos que la diferencia de potencial no es otra cosa que el voltaje, al cual nos referimos continuamente. El que haya poco voltaje significa que hay poca diferencia de potencial y que por lo tanto las cargas el�ctricas, en este caso electrones, fluyen en forma m�s err�tica y que en consecuencia tenemos menos corriente.
LEY DE LA AUSENCIA DE MONOPOLOS MAGN�TICOS
Nos hemos extendido en la discusi�n de la ley de Gauss porque los conceptos de flujo y carga son importantes en el estudio de la ley que ahora nos ocupa. En la figura 7 se muestran las l�neas de campo magn�tico y tal pareciera que hay un exceso de carga magn�tica positiva en un extremo del im�n y exceso de carga magn�tica negativa en el otro. As�, podr�a pensarse que existe una ley an�loga a la de Gauss para el caso magn�tico. Si tom�ramos una superficie que incluya una regi�n del espacio donde haya cargas o polos magn�ticos aislados, tendr�amos un flujo neto y por lo tanto una ley de Gauss magn�tica, con lo que se obtendr�a un campo magn�tico que decae de la misma forma que el inverso del cuadrado de la distancia a distancias grandes. Es un hecho, sin embargo, que la materia est� compuesta de cargas el�ctricas libres y no de cargas magn�ticas. Dicho de otra forma, los polos magn�ticos aislados parecen no existir y por lo tanto la ley para el flujo de campo magn�tico es diferente de la de Gauss y reza como sigue: el flujo neto de campo magn�tico a trav�s de cualquier superficie cerrada es cero. Esto es cierto para todo el espacio, pues no existen polos magn�ticos aislados.
Sin embargo, en principio no existe impedimento f�sico para pensar que en alg�n lugar del espacio (o en el pasado) existieron monopolos magn�ticos. A lo largo de este siglo ha habido numerosos intentos para localizar un monopolo magn�tico. Algunas modernas teor�as cosmol�gicas predicen que pares de polos magn�ticos fueron creados al principio del Universo para separarse posteriormente. Estos monopolos ser�an "pocos" comparados con el n�mero de electrones, por ejemplo, y dif�ciles de detectar. Esta fascinante b�squeda tal vez tendr� �xito en el futuro.
�Qu� incidencia tendr�a esto en la ley que ahora tratamos? Aparte de aseverar que el flujo magn�tico neto en algunos puntos del Universo no es cero, las conclusiones generales de la electrodin�mica no se ver�an afectadas pues, como ya dijimos, la materia est� compuesta de cargas el�ctricas y las fuentes del campo magn�tico son las corrientes el�ctricas, adem�s de que las interacciones cu�nticas son microsc�picas.
Para completar diremos que esta ley implica la existencia de una cantidad llamada potencial vectorial magn�tico, que es de suma importancia en la electrodin�mica.
Entre los f�sicos que empezaron a investigar la relaci�n entre electricidad y magnetismo, Faraday fue el que realiz� las contribuciones m�s importantes, junto con Amp�re. Aqu�l, entre otras cosas, encontr� que una aguja se magnetiza por el pulso de corriente inducida y que puede ser magnetizada en sentido opuesto cuando el circuito primario es desconectado. Esto es consecuencia de la fuerza que un campo magn�tico ejerce sobre una carga en movimiento. Si imaginamos un circuito movi�ndose en un campo magn�tico producido por una corriente uniforme y suponemos que una carga se mueve en el circuito, podemos definir a la fuerza electromotriz como la cantidad proporcional al trabajo que se hace para mover la carga en cuesti�n a lo largo del circuito. Si la resistencia del circuito es R, la fuerza electromotriz E har� circular una corriente 1 en el circuito de acuerdo con la ley de Ohm I=E/R. Esto indica que la fuerza electromotriz esta �ntimamente relacionada con la diferencia de potencial definida en p�rrafos anteriores. As�, la fuerza electromotriz es proporcional a la variaci�n temporal del flujo de campo magn�tico que ocurre al desplazarse el circuito (Figura 14).
Puede ocurrir que el circuito se agrande, cambie de forma, etc., dando lugar
a que cambie el flujo y por lo tanto se origine una fuerza electromotriz. �Qu�
direcci�n sigue la corriente en el circuito? Lenz aplic� el principio, basado
en la ley de conservaci�n de la energ�a, de que un sistema f�sico tiende a oponerse
a cambiar del estado en que se encuentra. De esta manera, si sucede que el flujo
que pasa por un circuito aumenta con el tiempo, aparecer� un nuevo flujo en
direcci�n opuesta producido por una corriente en el circuito. Como la direcci�n
de la corriente y del campo magn�tico est�n relacionadas, se puede obtener la
direcci�n de la corriente conociendo la direcci�n del flujo.
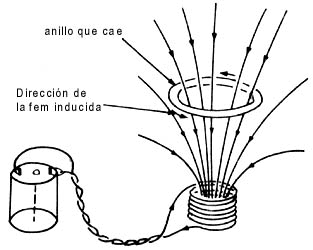
Figura 14. A medida que el anillo cae, el flujo a trav�s del anillo crece. Seg�n la ley de Lenz, la fuerza electromotriz inducida seguir� la direcci�n de las flechas.
En resumen, al mover un circuito en un campo magn�tico, la fuerza electromotriz inducida genera una nueva corriente el�ctrica en el circuito, que es proporcional al flujo del campo magn�tico. Faraday demostr� que lo mismo ocurre cuando se var�a la corriente y el circuito se mantiene en reposo, en lugar de mantener constante la corriente que genera el campo magn�tico en donde se mueve el circuito. Estas dos situaciones son equivalentes y a partir de ellas podemos enunciar la ley de inducci�n, en forma general, como sigue: la fuerza electromotriz inducida en un circuito es proporcional a la variaci�n temporal del flujo del campo magn�tico que rodea al circuito.
Como la fuerza electromotriz se relaciona con el campo el�ctrico, la ley establece una relaci�n entre el campo el�ctrico en una trayectoria cerrada y la raz�n de cambio temporal del campo magn�tico (Figura 14). Esta ley es una relaci�n fundamental que nos muestra c�mo se induce un campo el�ctrico al variar el campo magn�tico. Como no existen monopolos magn�ticos, no habr� corrientes magn�ticas que induzcan un campo el�ctrico.
El hecho experimental con el que se relaciona esta ley es la producci�n de campos magn�ticos cuando circula una corriente. Como vimos en el cap�tulo 1, este descubrimiento, debido a Oersted, conmocion� al mundo cient�fico. Ampère descubri� m�s tarde que si una corriente el�ctrica estacionaria circula por un alambre y trazamos una trayectoria cerrada alrededor del alambre, entonces el producto del campo magn�tico originado por la corriente, por la longitud de esta trayectoria, es proporcional a la corriente. El resultado llev� a Ampère a proponer que el magnetismo en la materia es causado por corrientes de electrones en sus �rbitas.
Por cierto tiempo se crey� que s�lo la corriente el�ctrica generaba un campo magn�tico. Sin embargo, faltaba un elemento que el genio de Maxwell aport�. Su razonamiento fue el siguiente. Como la carga el�ctrica est� compuesta de cargas en movimiento y la carga no se crea ni se destruye, la llamada ecuaci�n de continuidad establece que si la carga var�a con el tiempo en un punto del espacio, existe una fuente o sumidero de corriente en ese punto. Recordemos que la ley de Amp�re es v�lida para corrientes estacionarias que no var�an con el tiempo. Supongamos ahora que tenemos una distribuci�n de cargas que var�an con el tiempo. Se debe entonces agregar un t�rmino a la ley de Amp�re. Este t�rmino proviene del hecho de que al variar un campo el�ctrico se origina un campo magn�tico. En ausencia de corriente el�ctrica �ste deberla ser el �nico efecto que generara un campo magn�tico. Notemos que el caso es an�logo a lo que sucede en la ley de Faraday y que al agregar este t�rmino Maxwell hizo sim�tricas las ecuaciones (Figura 10). �Por qu� Faraday no not� este efecto en sus experimentos? Esto se debe a que en cualquier aparato en el cual var�a el campo el�ctrico, �ste lo hace en forma muy lenta. Para hallar el efecto se necesita que el campo cambie r�pidamente, tan r�pidamente como el tiempo que la luz tarde en cruzar el aparato, o sea tiempos peque��simos. Usando microondas, Hertz comprob� la existencia de este efecto predicho por Maxwell.
Por lo tanto, se puede enunciar la ley como sigue: la raz�n de variaci�n temporal del campo el�ctrico m�s la corriente estacionaria producida por cargas en movimiento es proporcional al campo magn�tico a lo largo de una trayectoria cerrada.
As�, hemos presentado las cuatro leyes fundamentales del electromagnetismo. A continuaci�n examinaremos c�mo fueron usadas por Maxwell para predecir que la luz es una onda electromagn�tica que se desplaza en el vac�o.
LA LUZ ES RADIACI�N ELECTROMAGN�TICA
�C�mo es que Maxwell predijo a partir de sus ecuaciones que la luz es una onda
electromagn�tica, es decir que consiste en campos el�ctricos y magn�ticos propag�ndose
en �ngulos rectos uno con respecto al otro? Antes de responder a la pregunta
anterior, aclaremos que por luz entendemos en esta secci�n todo el espectro
de radiaciones electromagn�ticas. Una onda se propaga con cierta velocidad y
frecuencia y las caracter�sticas de la misma var�an con �sta. Las ondas de muy
baja frecuencia o longitud de onda larga son ondas de radio. Al aumentar la
frecuencia tendremos las conocidas microondas, despu�s la radiaci�n infrarroja,
hasta llegar a un peque�o intervalo de 1014 ciclos/seg donde encontraremos la
luz visible, del rojo al azul. Sigue despu�s la radiaci�n ultravioleta y a altas
frecuencias los rayos X. Pues bien, en este espectro de radiaci�n tenemos ondas
electromagn�ticas que se transmiten a una velocidad constante y con frecuencia
distinta. A mayor frecuencia, mayor es la energ�a transportada.
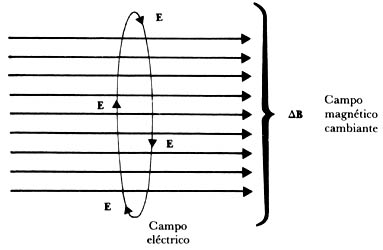
Figura 15. Un campo magn�tico que cambia uniformemente (DB) produce un campo el�crtico estacionario en un aro de alambre. Si el campo magn�tico cambia en forma no uniforme, produce un campo el�ctrico cambiante en el aro de alambre.
La predicci�n de Maxwell se basa en dos pilares: el descubrimiento de que existe un campo magn�tico asociado a cargas en movimiento estacionario, adem�s de que (y �sta fue su gran aportaci�n) una variaci�n del campo el�ctrico induce tambi�n un campo magn�tico, y el descubrimiento de Faraday de que un campo magn�tico variante induce una corriente. Si el lector escudri�a la figura 10, haciendo cero la carga p y la corriente J debida a las cargas en movimiento, ver� que las dos �ltimas ecuaciones son sim�tricas y que ante una sustituci�n de E por -B ser�n completamente invariantes.
Maxwell interpret� y conect� estas dos leyes imaginando un circuito en el espacio, tal como se muestra en la figura 15.
Supongamos que existe un campo magn�tico no uniforme que var�a con el tiempo. La ley de Faraday nos indica que este campo inducir� una fuerza electromotriz que a su vez producir� una corriente que representa un campo el�ctrico no uniforme variando en el tiempo. Este campo a su vez produce un campo magn�tico no uniforme que se desplazar� en el espacio. Para evitar complicaciones con la forma y tama�o del circuito, hag�moslo infinitamente peque�o. De esta forma y en lenguaje campista ocurre que en alg�n punto del espacio un campo magn�tico variante inducir� un campo el�ctrico variante (aun sin circuito), el cual a su vez inducir� un campo el�ctrico en otro punto del tiempo y del espacio y as� sucesivamente. De esta manera se genera una onda electromagn�tica donde los campos aqu� y ahora dependen de c�mo eran los campos en el pasado y de la posici�n inmediatamente anterior.
Maxwell, a continuaci�n, propuso la hip�tesis de que estas ondas eran ondas transversales. Al generarse uno al otro, el campo magn�tico y el el�ctrico lo hacen a �ngulos rectos, y de tal forma que la onda de luz se propaga tambi�n en �ngulos rectos respecto a los dos campos (Figura 16).
Adem�s, prob� que la velocidad de transmisi�n de las ondas electromagn�ticas era 3 X l05 km/seg en el vac�o.
Lo que hemos descrito brevemente, sin duda representa uno de los logros culminantes de la f�sica en todos los tiempos. Cuando los resultados fueron publicados en 1873, pocos cient�ficos captaron todas las consecuencias que se derivaban de esta teor�a.
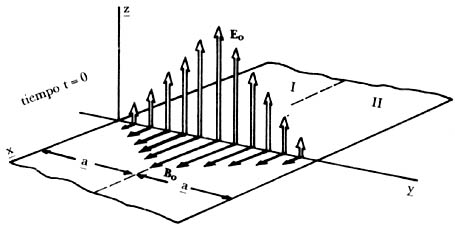
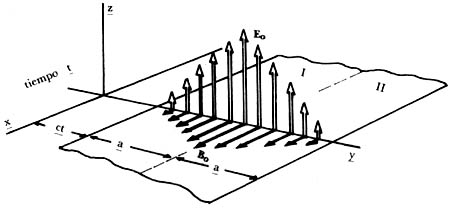
Figura 16. Configuraci�n de campos el�ctrico y magn�tico que viajan con velocidad c en la direcci�n y.
La teor�a tuvo que aguardar alrededor de 15 a�os para su confirmaci�n experimental por Hertz, quien, para dise�ar su experimento, utiliz� el hecho, enfatizado por Maxwell, de que para producir una onda electromagn�tica se tiene que excitar una carga para ponerla en movimiento y as� generar la radiaci�n. Hertz dispuso de un generador que produc�a ondas con frecuencia de 108 ciclos/seg, o sea microondas, y no produjo luz visible.
Queremos por �ltimo enfatizar que las ondas electromagn�ticas pueden superponerse, ya que por fortuna las ecuaciones de la electrodin�mica son lineales en los campos. Si dos conjuntos de campos satisfacen las ecuaciones, su suma tambi�n lo hace, y as� cualquier superposici�n de ondas electromagn�ticas planas tiene las caracter�sticas generales de las ondas originales; a saber:
1) viajan a la velocidad de la luz, sin cambiar forma, cualquiera que �sta sea;
2) el campo magn�tico y el�ctrico son perpendiculares uno al otro y a la direcci�n de propagaci�n de la onda, y
3) en cualquier tiempo y lugar la magnitud del campo el�ctrico es igual a la del magn�tico.
Hasta ahora hemos descrito a los campos en el vac�o y no hemos hecho menci�n de su comportamiento cuando interact�an con la materia. Coment�bamos m�s atr�s que el estudio del concepto de campo hab�a incidido enormemente en el estudio de los materiales magn�ticos, ya que pod�a englobar dentro de un esquema conceptual �nico una gran cantidad de fen�menos. En esta secci�n nos limitaremos a estudiar campos magn�ticos interactuando con la materia, mencionando s�lo de pasada algunos elementos sobre los campos el�ctricos. Es de hacer notar que no describiremos c�mo la electrodin�mica se une a la termodin�mica para entender los cambios de energ�a que ocurren al efectuar un proceso f�sico en materiales magn�ticos, puesto que eso ser�a el tema de un libro aparte. Para iniciar nuestra discusi�n, supongamos que tenemos una bobina que produce campos magn�ticos muy fuertes. �Qu� ocurre si sometemos diversas sustancias al efecto de este campo? Sabemos que las part�culas de estos materiales sufren una fuerza proporcional a la masa de la muestra. Sin embargo, otros resultados no muestran un comportamiento sistem�tico: unas sustancias son jaladas hacia la direcci�n en donde el campo es mayor, otras hacia donde disminuye, otras m�s apenas parecen sentir el intenso campo magn�tico al cual est�n sometidas, etc. Por ejemplo, el ox�geno l�quido puede sentir una gran fuerza, mientras que el nitr�geno apenas si se entera de que hay un campo. Esto nos indica la gran variedad de materiales magn�ticos que existen y el intervalo tan grande en que la fuerza magn�tica ejerce su acci�n. Obviamente el hierro parece ser "m�s magn�tico" que otras sustancias (v.g., cinco �rdenes de magnitud respecto al cobre). Adem�s, para algunas sustancias la fuerza que act�a sobre ellas var�a de la misma forma que el cuadrado del campo, mientras que para los �xidos de hierro o el hierro mismo var�a lentamente. Es conveniente clasificar a las sustancias de acuerdo a su comportamiento para poder aplicar las leyes estudiadas en las secciones anteriores, debidamente modificadas, para tomar en cuenta que hay materia. As�, las sustancias que son repelidas por los imanes son llamadas diamagn�ticas, por ejemplo el agua y los compuestos org�nicos. De hecho, todas las sustancias son diamagn�ticas, pero en algunas de ellas otros efectos son m�s importantes.
Las sustancias atra�das hacia campos m�s fuertes son llamadas paramagn�ticas. En algunos metales el paramagnetismo es d�bil y en otros fuerte. Adem�s, a bajas temperaturas el paramagnetismo aumenta, tal como sucede con el ox�geno l�quido.
Finalmente, las sustancias que se comportan como el hierro y la magnetita son llamadas ferromagn�ticas.
�C�mo podemos descubrir este comportamiento de la materia sin recurrir a un modelo microsc�pico? �Pueden adaptarse las leyes macrosc�picas para entender estos tipos de magnetismo? Para empezar, hay que tener presente que en su interacci�n con la materia el campo magn�tico juega un papel radicalmente distinto al campo el�ctrico, pues la materia est� hecha de cargas el�ctricas y corrientes el�ctricas y no existen cargas o corrientes magn�ticas. De all� que esperemos que las fuerzas el�ctricas dominen el comportamiento de la materia.
Dejaremos para el siguiente cap�tulo la descripci�n de modelos microsc�picos
para explicar el magnetismo. S�lo recordaremos que las explicaciones dadas por
Ampère y otros f�sicos del siglo XIX y principios del siglo
XX consideraban que el magnetismo era causado por las corrientes
at�micas que al crear campos macrosc�picos determinaban las caracter�sticas
magn�ticas de la materia.
Para caracterizar macrosc�picamente las diversas sustancias es conveniente introducir el concepto de momento magn�tico. Este se define como la cantidad proporcional al producto de la corriente que se mueve en un circuito por el �rea encerrada por el mismo. Si aplicamos un campo magn�tico externo veremos que la fuerza sobre este dipolo es proporcional al campo magn�tico, y el resultado experimental es que las sustancias paramagn�ticas y diamagn�ticas adquieren un momento magn�tico proporcional al campo. Esta relaci�n es lineal y podemos definir a la susceptibilidad magn�tica X como la raz�n entre el momento magn�tico y el campo. Para sustancias diamagn�ticas la susceptibilidad es peque�a y menor que cero, del orden de -1 x 106. Para materiales paramagn�ticos X es positiva y un poco mayor. Por lo tanto, podemos afirmar que en estas sustancias el campo aplicado que act�a sobre los dipolos magn�ticos es el mismo que en el vac�o. Sin embargo, en otro sistema el campo producido por los momentos magn�ticos es grande, por lo que deber�amos tomar en cuenta estos campos y adicionarlos al campo aplicado. Aqu� es conveniente hacer notar que las corrientes pueden clasificarse como corrientes libres y ligadas. Las primeras corresponden a corrientes macr�sc�picas, mientras que las segundas est�n asociadas a corrientes moleculares, es decir a la fuente de la magnetizaci�n del material. Las corrientes libres est�n asociadas a un nuevo campo magn�tico H, distinto de nuestro conocido campo magn�tico B, mientras que este �ltimo est� asociado a la corriente total. De paso mencionaremos que nuestro conocido campo el�ctrico E est� asociado a la carga total. La diferencia entre H, llamado desplazamiento magn�tico, y el campo B, es obviamente proporcional a la magnetizaci�n del material, y su raz�n es la llamada permeabilidad magn�tica. De hecho, para estudiar los campos originados por corrientes libres deber�a usarse el desplazamiento magn�tico. Sin embargo, consideramos que el campo magn�tico fundamental es B, ya que no existen cargas magn�ticas libres.
Habiendo examinado someramente la susceptibilidad magn�tica para sustancias
diamagn�ticas y paramagn�ticas, pasemos a estudiarla cuando el material es ferromagn�tico.
El lector se habr� dado cuenta que el ferromagnetismo es el fen�meno que atrajo
la atenci�n del hombre hacia la magnetita, puesto que es magnetismo "permanente".
La fuerza sobre una sustancia paramagn�tica es proporcional a la variaci�n del
campo, lo que sugiere que, si el campo es muy fuerte, el momento magn�tico de
un ferromagneto alcanza un l�mite. Aun sin campo externo los ferromagnetos conservan
su magnetizaci�n, pero la pierden al elevarse la temperatura.
Figura 17. Se muestran los dominios magn�ticos en un material ferromagn�tico
orientados al azar. Sin embargo, en cada uno de ellos todos los dipolos magn�ticos
se al�nean en una direcci�n dada por las flechas.
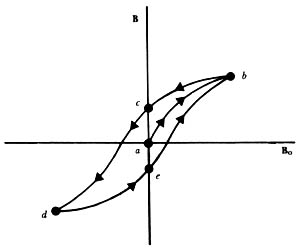
Figura 18. Curva de magnetizaci�n (ab) y su curva asociada de hist�resis (ebcde) para una muestra de hierro.
Su magnetizaci�n es mucho mayor que la de los materiales paramagn�ticos. Todo esto sugiere que los dipolos magn�ticos deben estar "amarrados" en una direcci�n por "algo" de naturaleza distinta a los mecanismos discutidos hasta ahora.
Por ejemplo, el hecho de que a determinada temperatura se destruya el ferromagnetismo indica que los momentos magn�ticos no est�n alineados. Por supuesto que los materiales est�n compuestos de los llamados dominios magn�ticos que ser�n estudiados en el siguiente cap�tulo, en donde millones de momentos est�n alineados en una direcci�n (Figura 17). Si hay m�s dominios con un momento magn�tico promedio en una direcci�n determinada, el material estar� magnetizado.
�Cu�l es la relaci�n entre la magnetizaci�n y el campo en un ferromagneto? Supongamos que tomamos hierro demagnetizado y aplicamos un campo externo, el cual hace variar B que, recordemos, est� relacionado con la corriente total.
En la figura 18 podemos ver que al incrementar el campo externo los dominios se alinean f�cilmente, pero que despu�s se necesita un campo mayor para conseguir una peque�a variaci�n de las corrientes ligadas. Si ahora disminuimos el campo externo, veremos que la curva no retorna al punto de partida por el camino que segu�a al aumentar el campo.
�ste es el fen�meno de hist�resis que se debe a la irreversibilidad del proceso
y que es indispensable para obtener una magnetizaci�n permanente. Con esto concluimos
este cap�tulo, para pasar en el siguiente a examinar los fundamentos microsc�picos
del magnetismo.
