III. EL MAGNETISMO Y EL ÁTOMO: DESCRIPCIÓN MICROSCÓPICA

INTRODUCCIÓN:

ESTRUCTURA ATÓMICA DE LA MATERIA

EL CAPÍTULO anterior muestra los avances en la descripción de la teoría electromagnética que fueron y son de gran utilidad, pero no resuelven el misterio del origen microscópico de los fenómenos electromagnéticos, los cuales son, se podría decir, la última causa de los efectos que vemos. Expondremos aquí una teoría de las propiedades eléctricas y magnéticas de la materia fundamentada en la física atómica moderna y la mecánica cuántica.

Hubo un famoso intento de reformular la teoría electromagnética como una teoría microscópica partiendo de nuestro conocimiento de la existencia del electrón debida a Lorentz, llamada teoría del electrón. Como mencionamos al principio del libro, el modelo de Lorentz se topó con la necesidad de una teoría más completa. El electrón no es una partícula clásica y por tanto obedece las leyes de la física cuántica.

Actualmente sabemos que la materia está formada por átomos. Estos tienen su estructura propia, pero para nuestros propósitos bastará con que los consideremos como núcleos cargados positivamente, alrededor de los cuales giran electrones cargados negativamente, de tal manera que los átomos como un todo son neutros en su estado natural. Los electrones al girar en sus órbitas producen un campo magnético semejante al de un imán, como sabemos por la teoría electromagnética. Así, desde el punto de vista de sus propiedades magnéticas, los materiales están formados por pequeños imanes que, si el material no manifiesta magnetización, necesariamente están orientados al azar. Cuando se somete un material a la acción de un campo magnético, pueden darse dos mecanismos.

En el primero los imanes simplemente se alinean en la dirección del campo aplicado, como las brújulas en la Tierra. Este efecto se llama paramagnetismo y este alineamiento produce una resultante en la misma dirección del campo, dando como resultado que el material se comporte como un imán que es atraído en el sentido de ese campo. En el segundo mecanismo, llamado diamagnetismo, el material también se comporta como un imán, pero que se opone al campo que lo produce, siendo repelido por éste. Aquí el campo externo obliga a los imanes atómicos a procesar en la dirección del campo, generando un momento magnético. También podemos ahora entender el efecto de la temperatura en los fenómenos magnéticos, ya que los átomos están también sujetos a movimientos térmicos que se oponen a que se alineen en una cierta dirección.

Entender el ferromagnetismo es más difícil. Estos materiales presentan porciones que tienen magnetización completa y permanente y se llaman dominios ferromagnéticos. Fue Pierre Weiss en 1907 quien se dio cuenta de que los materiales ferromagnéticos están formados por estos dominios, los cuales pueden inclusive orientarse de tal manera que el material no exhiba propiedades magnéticas (Figura 19).

Con un campo magnético externo los dominios se pueden reorientar o crecer hasta formar un imán. Como ya lo hemos mencionado, este proceso de magnetización es irreversible. Para explicar la existencia de los dominios también se puede pensar en términos de pequeños imanes, pero que están formados por los propios electrones, los cuales poseen un movimiento magnético intrínseco llamado espín. La acción conjunta de los espines dentro de un dominio obedece a la fuerza de intercambio que es de naturaleza cuántica y no tiene análogo en la física clásica.

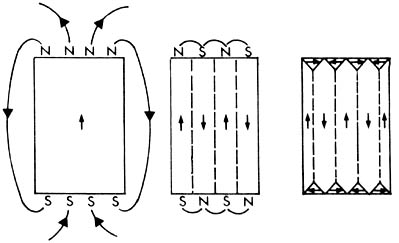
Figura 19. Los dominios magnéticos pueden formar diferentes patrones, para minimizar la energía. Se pueden observar experimentalmente por ejemplo con un microscopio electrónico. Los dominios magnéticos se pueden mover por medio de campos externos.

El hecho de que el electrón se comporte como un pequeño imán nos lleva a suponer que todas las partículas elementales cargadas podrían tener momento magnético. De hecho así es y la teoría de las partículas elementales incluye el estudio de sus momentos magnéticos. Pero cuidado, la teoría electromagnética es una teoría macroscópica, basada en experimentos en la escala de nuestras proporciones y el reino de las partículas elementales puede deparar muchas sorpresas.

SUSTANCIAS MAGNÉTICAS

Como mencionamos en el capítulo 1, las propiedades térmicas de las sustancias magnéticas fueron estudiadas por Pierre Curie, quien estableció que la susceptibilidad magnética de las sustancias paramagnéticas depende del inverso de la temperatura. En todos los ferromagnetos encontró un descenso de la magnetización hasta que la temperatura llegaba a un valor crítico, llamada temperatura de Curie (Tc), donde la magnetización se hace igual a cero (Figura 20); arriba de la temperatura de Curie, los ferromagnetos se comportan como sustancias paramagnéticas. También existen otros ordenamientos magnéticos (antiferrimagnético y ferrimagnético) cuyos modelos microscópicos serán discutidos en el siguiente capítulo.

El diamagnetismo lo explicó Paul Langevin una década después de los experimentos de Curie. El fenómeno se puede explicar usando las leyes de Maxwell. Cuando se enciende un campo magnético, aparece un campo eléctrico. Éste acelera a un electrón, produciéndose así una corriente, la cual crea una magnetización contraria al campo aplicado, según la ley de Lenz.

Esta explicación implica suponer que la ley de Lenz se cumple a escala atómica. Ya Coulomb sabía que las leyes ordinarias de electrostática y magnetoestática no podían ser válidas en la escala atómica. Con esa misma filosofía, Pierre Weiss supuso que las interacciones entre las moléculas magnéticas se podrían descubrir empíricamente, por lo que introdujo el campo molecular sin intentar describir las leyes microscópicas. Este campo molecular actuaría sobre cada molécula como un campo externo y sería proporcional a la magnetización y al tipo de material. Su modelo llevó a la ley Curie-Weiss, que obedecen practicamente todos los ferromagnetos. Esta coincidencia tan perfecta hizo difícil hacerle mejoras.

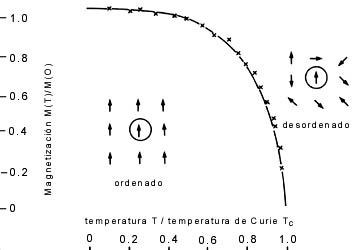
Figura 20. El campo molecular de Weiss. Un espín escogido (en círculo) en un material magnético experimenta un campo debido a los otros espines. La magnetización se hace cero en temperatura de Curie Tc .

Existía en esa época un enigma experimental: ¿por qué no es el hierro espontáneamente ferromagnético? Weiss propuso que su campo molecular tenía diferentes direcciones en algunos pedazos del sólido. Esto fue probado por Barkhausen en 1919, quien por medio de amplificadores electrónicos oyó los "clics" cuando un campo externo obliga a los dominios de Weiss a alinearse. Este es un comportamiento irreversible que explica el fenómeno de histéresis. Medidas de la razón giromagnética en ferromagnetos probaron además que éste no es magnetismo atómico o molecular, sino que sólo el espín electrónico participa de él.

Así pues, a pesar de la belleza de los argumentos de Lorentz y Langevin para aplicar la teoría electromagnética a nivel microscópico, resultó inevitable reconocer que a escala atómica había algo nuevo y diferente y que hacía falta una nueva teoría para enfrentarse a este mundo. De hecho, con el teorema de Bohr-Van Leeuwen quedó claro que la mecánica estadística clásica de las partículas cargadas no es capaz de explicar el comportamiento de ninguna de las sustancias magnéticas descritas aquí.

TEORÍA CUÁNTICA

De 1913 a 1925 se desarrolló la "vieja mecánica cuántica". Bohr cuantizó el átomo de Rutherford y se empezó a entender bien la estructura de la materia. En 1921, Compton propuso que el electrón posee un espín intrínseco (gira sobre sí mismo) y momento magnético, además de su momento angular orbital y su magnetización.

Esto fue probado en 1925 por S. Goudsmit y G. E. Uhlenbeck, quienes demostraron que el espín del electrón es / 2 (con = , h la constante de Planck) y al momento magnético le asignaran el doble del esperado para una partícula cargada girando. En 1896 Zeeman mostró que las líneas espectrales se podían descomponer en conjuntos, llamados multipletes, si los átomos emisores se sujetan a campos magnéticos intensos. La teoría del electrón de Lorentz dio una explicación razonable de este efecto. Sin embargo, el efecto Zeeman anómalo ya no pudo ser explicado de la misma manera. En él se observó que las líneas D del sodio, en presencia de un campo magnético fuerte, se partían en cuartetos y multipletes mayores. Landé, al estudiar el efecto Zeeman anómalo, introdujo el famoso factor g y Goudsmit y Uhlenbeck le asignaron un factor de g = 2 al espín del electrón para que concordaran los resultados. Este factor de dos sólo se entendió bien algunos años más tarde cuando Dirac unió la teoría de la relatividad con la mecánica cuántica.

La mecánica cuántica se desarrolló muy rápidamente. En 1923 De Broglie introdujo la mecánica ondulatoria: el electrón no es simplemente una partícula, sino que también tiene características de onda. En 1926 aparece la ecuación de onda debida principalmente a E. Schröedinger y equivalente a la ecuación de movimiento de la mecánica clásica de Newton. Mientras tanto, W. Heisenberg y H. A. Kramers probaron que se podría escribir esta mecánica en forma matricial y Max Born y Norbert Wiener colaboraron en demostrar que a cada cantidad física le corresponde un operador. La conexión entre teoría cuántica y mecánica estadística surge desde la cuantización de la radiación hecha por Planck en 1900.

La mecánica cuántica incluye el llamado principio de incertidumbre de Heisenberg que limita nuestro poder de información. Cuando estamos en el mundo microscópico, donde la constante de Planck se vuelve importante, no podemos conocer exactamente la posición y la velocidad de una partícula en forma simultánea. Precisar una implica perder precisión en la otra. En 1927 Pauli inventó las matrices de espín y su principio de exclusión, el cual volveremos a mencionar en un momento.

Simultáneamente al desarrollo de la mecánica cuántica, Hartree, Fock, Heiter, London, Slater y muchos otros hacían cálculos atómicos y moleculares como una de las aplicaciones de la nueva ciencia. Para 1930, fecha del famoso y ya mencionado congreso de Solvay sobre magnetismo, ya se habían sentado las bases de la teoría moderna de la materia y sus propiedades.

EL ESPÍN

En 1921 Arthur Compton, un joven físico estadounidense quien trabajaba con Rutherford en Cambridge, tuvo la idea de que el electrón debería poseer un momento angular intrínseco o espín y por lo tanto actuar como un imán.

Este espín no se debe confundir con el momento magnético que se produce al orbitar un electrón alrededor de un núcleo, el cual, además, era conocido. Compton tenía una base para proponer el espín, pues diversos experimentos no podían ser explicados de manera satisfactoria. Uno de ellos, el llamado experimento de Einstein-de Hass (1915) mostró que el factor de Landé o razón giromagnética valía 2 en vez de 1 como la teoría predecía. Esta razón giromagnética mide la razón entre el momento magnético y la componente del momento angular en una dirección. Para medirlo, se suspende una barra magnética de una fibra de cuarzo y se magnetiza pasando corriente por un alambre enredado en ella. De esta forma la barra adquiere un momento magnético y un momento angular que se determina por medio de la rotación angular de la fibra de cuarzo. La magnetización se debe por entero al movimiento de los electrones, pues la razón es negativa.

Además de este experimento, existían otros, tales como el efecto Zeeman anómalo, que estaban en desacuerdo con la teoría en boga. En 1925, Wolfgang Pauli investigó el problema de por qué las líneas del espectro de los metales alcalinos no eran singuletes como lo predecía la teoría de Bohr sino un doblete, o sea, había dos líneas en vez de una. Esto podía ser explicado si se suponía que el electrón podía existir en dos estados. Sin embargo, el experimento crucial que mostró la existencia del espín fue realizado por Otto Stern y Walter Gerlach en 1921. En su clásico experimento, un haz de átomos monovalentes, como el hidrógeno, el litio o la plata, viajaban a lo largo de un eje atravesando un campo magnético perpendicular a dicho eje. Había gradientes muy grandes, ya que el campo era inhomogéneo. En sus experimentos, Stern y Gerlach estudiaron la división del haz de átomos en el estado base y en estados excitados. Se esperaba que en el estado base no hubiera división, pero se encontró que el haz se dividía en dos componentes. El análisis mostró que este efecto podía ser consecuencia del electrón en la parte más externa del átomo. La proyección del momento magnético del estado base podía tomar, pues, dos valores. Esto condujo a G. Uhlenbeck y S. Goudsmit a introducir la hipótesis que un electrón posee un momento angular intrínseco en adición a su momento angular orbital. Uhlenbeck y Goudsmit, quienes por cierto no recibieron el premio Nobel, mostraron que los multipletes espectrales podían ser explicados con esta hipótesis, introduciendo el espín s que podía tomar dos valores, + ó — , de tal forma que el momento angular intrínseco del electrón era + ó — . Además, se podía explicar el valor de dos para el factor de Landé en el experimento de Einstein-de Hass.

El concepto de espín electrónico apareció al principio como una hipótesis extra que debía ser agregada al resto de la teoría cuántica. Se pensaba que el espín podía ser tratado en forma análoga a un trompo girando sobre su eje. Debe enfatizarse, sin embargo, que no existe una teoría clásica rigurosa del espín.

La culminación de estos estudios fue la formulación por Dirac de su famosa ecuación dinámica, la cual incluye el espín electrónico y la relatividad especial. En su teoría, las propiedades del espín se obtienen en forma natural de la misma y no se necesitan hipótesis adicionales.

No se puede subestimar la influencia del espín en la física moderna. Puede afirmarse que éste es uno de los conceptos centrales de esta ciencia, y tanto en la física cuántica como en los fenómenos cooperativos ha jugado un papel fundamental para entender una gran diversidad de fenómenos.

INTERCAMBIO

Retomemos el problema del ferromagnetismo, pero esta vez como un fenómeno colectivo. ¿Qué entendemos por un fenómeno colectivo? Supongamos que caminamos en una calle bastante transitada y que a dos cuadras adelante de nosotros ocurre un accidente. De inmediato esa información se transmite por medio de la gente en forma de un movimiento colectivo y por tanto nos enteramos de qué pasó bastante antes de verlo. Es claro que un fenómeno así involucra a muchas personas. Esto es lo que en física se llama un fenómeno de muchos cuerpos. Cabe adelantar que el estudio del magnetismo como un fenómeno cooperativo desempeñó un papel decisivo en la mecánica estadística cuántica y en la termodinámica de las transiciones de fase. Hoy, con la teoría del grupo de renormalización, el estudio de las transiciones de fase es uno de los campos más importantes en el estudio de la materia.

El problema para poder explicar el ferromagnetismo consiste en lo siguiente: ya sea que los pequeños imanes que forman la materia sean electrones en sus órbitas o espines de electrones, las fuerzas magnéticas entre ellos no son lo suficientemente intensas para producir un ferromagneto. La interacción magnética se puede despreciar comparándola a la fuerza electrostática entre electrones. Con una simultaneidad que se ha repetido muchas veces en la historia de la ciencia, Dirac y Heisenberg descubrieron la fuerza de intercambio. Este efecto es bastante misterioso, ya que es totalmente cuántico y no tiene análogo clásico; ñel ferromagnetismo no existiría si la constante de Planck h fuera cero!

Cuando Pauli introdujo su notación matricial para el espín, quedó claro que el espín es una cantidad vectorial. Esto implica que podemos imaginárnoslo como una flechita. ¿Qué puede suceder si tenemos dos electrones cada uno con su flecha de espín asociados y alineados ambos en alguna dirección? Pues que los espines podían quedar paralelos o antiparalelos, lo que se ve claramente en la figura 21.

Figura 21. Las flechas representan espines paralelos y antiparalelos.

Cada electrón dentro de un átomo está caracterizado por un conjunto de números cuánticos que nos dicen sus propiedades físicas. El principio de exclusión de Pauli establece que no puede haber dos electrones en un átomo con el mismo conjunto de números cuánticos. Esto implica que en una misma órbita sólo puede haber dos electrones, ya que la órbita da una serie de características comunes y sólo queda la posibilidad de que los espines sean antiparalelos. Este principio de exclusión lo cumplen todas las partículas que tienen espín fraccionario, como es el caso del electrón.

Tenemos entonces que, por un lado, los electrones sufren una repulsión electrostática (ley de Coulomb) y, por otro, que tienen que cumplir el principio de exclusión. Por dicho principio los espines paralelos tienden a separarse y eso reduce su repulsión. Se llama "intercambio" a la diferencia de energía entre la configuración de espines paralelos y la configuración de espines antiparalelos. Esta energía de intercambio favorece al ferromagnetismo solamente si el aumento de energía cinética causado por la separación es mayor que el descenso en la energía potencial electrostática. Los detalles de esta interacción son complicados, pero lo importante es apreciar que las fuerzas involucradas son eléctricas y que son mucho más intensas que las magnéticas, entendiéndose así el llamado magnetismo fuerte.

Con este modelo, cuando la temperatura está abajo de la temperatura crítica, se producen las llamadas "ondas de espín" (Figura 22). Se forma una onda magnética en el material, en la cual participan todos los espines o pequeños imanes. Como se observa es claramente un efecto cooperativo. Arriba de la temperatura crítica las vibraciones térmicas son demasiado importantes y desaparecen las ondas de espín. Además las ondas de espín están cuantizadas y esos cuantos se llaman magnones. Pero aquí vamos a dejar ya la historia microscópica del magnetismo.

A pesar de que se ha investigado mucho sobre el intercambio no se ha logrado enunciar un postulado universal de primeros principios, como lo son las leyes de Maxwell o las de Newton en la mecánica clásica, De hecho, se tienen sólo descripciones semicuantitativas que aunque exitosas en algunos aspectos, pueden todavía ser mejoradas.

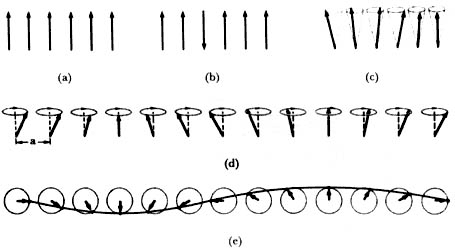
Figura 22. (a) Estado base de un ferromagneto simple: todos los espines paralelos. (b) una excitación posible: un espín se invierte. (c) Se forma una onda de espín: el extremo del espín precesa formando conos. (d) Una onda de espín vista en perspectiva. (e) Espines vistos desde arriba. La onda se dibuja por la punta de los espines.