XII. UNIFICACIÓN ELECTRODÉBIL: SALAM, WEINBERG, VAN DEER MEER Y RUBBIA
EXISTE una relación muy estrecha entre el concepto de partícula y el de fuerza. A las partículas se les clasifica según el tipo de fuerza al que son sensibles, mientras que los campos de fuerza son transmitidos por partículas. Otra idea íntimamente ligada a las partículas y fuerzas es la de simetría. Hasta ahora se ha revisado el avance en el descubrimiento de la estructura más elemental de la materia en lo referente a sus partículas. Este capítulo enfoca la evolución de la idea de una fuerza elemental, las simetrías encontradas, sus predicciones en términos de partículas intermediarias y su confirmación experimental.
El ser humano se vale constantemente de simetrías para aplicar a diversas situaciones una cantidad reducida de leyes físicas fundamentales. Galileo y Newton, por ejemplo, descubrieron que las leyes de la caída libre son simétricas con respecto a los desplazamientos en la posición, la orientación y el tiempo. O sea, si se eliminan factores externos, la descripción del movimiento es independiente de dónde se realicen los experimentos, desde qué ángulo se les observe o cuándo ocurran.
Cada simetría tiene como consecuencia una ley de conservación, entendida ésta como una cualidad que no cambia en el tiempo. Por ejemplo, que los resultados de un experimento sean independientes del lugar en el que se realicen es una invariancia translacional en el espacio que implica la conservación del ímpetu o momento lineal. Lo inverso también es cierto: cuando una cantidad se conserva, esto indica la existencia de una simetría. La conservación de la energía implica una invariancia translacional en el tiempo, es decir, que no importa a partir de cuándo empezamos a medir el tiempo. La invariancia respecto de la orientación se refleja en la conservación del momento angular.
Hacia principios del siglo pasado se sabía de la existencia de tres tipos de fuerzas en la naturaleza: la gravitacional entre las masas, la eléctrica que actúa entre las cargas y la magnética entre los imanes. Los trabajos de Faraday y Ampñre demostraron la existencia de una simetría entre las fuerzas eléctrica y magnética al observar que cargas en movimiento generan campos magnéticos y que campos magnéticos variables generan corrientes eléctricas. La interdependencia de estas fuerzas indicó que se trataba de distintas manifestaciones de una sola fuerza: la electromagnética.
La formulación de la teoría de los campos correspondientes a las dos fuerzas mencionadas fue propuesta por James Clerk Maxwell (la electromagnética) en 1868 y por Albert Einstein (la gravitacional) a principios del presente siglo. Existen ciertas similitudes interesantes entre ellas, como el que ambas poseen alcance infinito, y que su dependencia con la distancia es la misma. Este parecido motivó a varios investigadores, entre ellos al propio Einstein y a Hermann Weyl, a tratar de unificarlas. Objetivo que, por cierto, aún no se ha logrado.
Hacia 1920 Einstein había obtenido una formulación matemática de la teoría de la relatividad general que describía la fuerza de la gravedad en términos de la estructura del espacio-tiempo. Ese año, Weyl descubrió que tanto la relatividad general como el electromagnetismo pertenecen a una familia denominada teorías de norma con simetría local.
Las simetrías se pueden clasificar como globales y locales. Para
ilustrar el concepto de simetría global, considérese un experimento en el que
se mida el campo eléctrico generado por un conjunto de cargas, de ambos signos,
colocadas arbitrariamente en un laboratorio. En esas condiciones, la teoría
de Maxwell establece que el campo eléctrico entre dos puntos se da simplemente
por la diferencia de potencial entre ellos. Esto implica una simetría, ya que
el campo permanece invariante ante la suma o resta, global, de un potencial
constante arbitrario.17![[Nota 17]](../imgs/mcommnt.gif)
Por depender de medidas relativas, el campo eléctrico es independiente de la
convención o escala que se haya escogido para medir la carga eléctrica. Esto
constituye una invariancia de norma global. El término norma se
refiere a la elección de una escala o patrón de longitud, si bien la palabra
también es comúnmente sustituida por calibre, aforo, o el término inglés
gauge.
Una teoría general del campo eléctrico debe tomar en cuenta, no sólo cargas estáticas, sino experimentos con cargas en movimiento. Si sólo actuase la fuerza eléctrica, el movimiento arbitrario de las cargas en el laboratorio rompería la simetría del campo electrostático. Sin embargo, al moverse, las cargas generan campos magnéticos que permiten restablecer la simetría en forma local. Es decir, cualquier cambio en el potencial eléctrico puede combinarse, localmente, con un cambio en el potencial magnético de manera que los campos eléctricos y magnéticos sean invariantes.
La teoría del campo asocia a cada fuerza algún tipo de partícula, o partículas intermediarias, es decir, responsables de acarrear la información del campo. A principios de siglo, Planck y Einstein propusieron al fotón como mensajero del campo electromagnético. En la década de 1930, se puso de manifiesto la existencia de dos nuevas fuerzas fundamentales, que sólo actúan a distancias nucleares: la fuerte y la débil. Por ese entonces, Yukawa sugirió que el emisario correspondiente al campo fuerte sería el mesón. Ahora creemos que no es el mesón, sino el gluón el responsable de esta tarea, aun cuando nadie ha visto un gluón libre. Otro campo sin partícula identificada experimentalmente es el gravitacional, si bien los esfuerzos por detectar gravitones no han sido pocos.
La primera formulación teórica sobre la fuerza débil fue propuesta por Enrico
Fermi en 1934. Esta téoría es una analogía con la del campo electromagnético
en el que las partículas interactuantes emiten y absorben fotones. Sin embargo,
el decaimiento b implica la emisión
de partículas (electrones o positrones) cargadas, por lo que debería haber partículas
intermediarias con carga eléctrica (véase figura 11), las denominadas partículas
W (weak = débil). En este sentido, y basado en la aparente similitud
de alcances entre las fuerzas nucleares, Yukawa propuso, en su primer trabajo
sobre el campo nuclear, que el mediador de la fuerza débil podía ser el mismo
mesón. Esta idea fue refinada, poco después, por varios autores, como Nicholas
Kemmer (alumno de Pauli) y el sueco Oskar Klein. En 1937 Kemmer propuso la existencia
de un tercer mediador, neutro. En 1938 Klein, usando una idea primitiva de grupo
de simetrías, sugirió que el compañero neutro de las W podía ser el propio
fotón. En los años cuarenta, las evidencias experimentales demostraron ciertas
similitudes entre el decaimiento b y
el decaimiento muónico del pion. Esto fue tomado como evidencia de la universalidad
de las interacciones débiles.
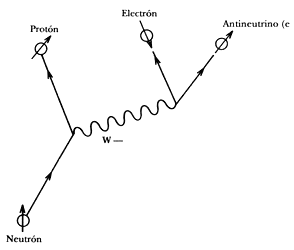
Figura 11. El decaimiento b del neutrón.
Según el modelo de los bosones intermediarios, este proceso ocurre en dos etapas.
Primero, el neutrón se transforma en un protón emitiendo una partícula W
virtual, misma que decae en una segunda etapa en un electrón y un antineutrino.
Ya que la creación de la W viola temporalmente la conservación de la
energía (de ahí lo virtual), la distancia que ésta recorre está limitada
por el principio de incertidumbre de Heisenberg.
La versión cuántico-relativista de la formulación de Maxwell, la electrodinámica cuántica, fue iniciada por Dirac hacia finales de la década de 1920 y, completada, en lo esencial, por Richard Feynman, Julian Schwinger y Sin-itiro Tomonaga hacia 1948. En la electrodinámica cuántica el electrón es representado como una onda. Para definir en forma completa una oscilación de este tipo deben conocerse su amplitud y su fase, la fase mide el desplazamiento de la onda desde un punto de referencia arbitrario. Experimentalmente sólo se pueden medir diferencias de fase, mas no la fase en sí. Es decir, esta teoría cuántica es invariante ante cambios globales de fase, lo que, nuevamente, constituye una simetría global de norma. Una formulación más general debe considerar cambios arbitrarios de fase. Como en el caso del electromagnetismo, este cambio altera la simetría global. La simetría se restablece localmente a través de la inclusión de un nuevo campo, el cual resulta ser el mismo campo electromagnético del fotón. Cuando un electrón absorbe o emite un fotón, las fases del campo del electrón y del fotón se combinan garantizando así la simetría de norma local. La ley asociada a esta simetría es la de la conservación de la carga eléctrica. Por su contribución, Feynman, Schwinger y Tomonaga recibieron el Premio Nobel en 1965.
A mediados de la década de 1950, había evidencias de una relación íntima entre las interacciones electromagnéticas y las débiles por el hecho de que el momento angular intercambiado en procesos débiles es unitario, idéntico al del fotón. Sin embargo, el corto alcance de la fuerza débil revelaba que, de existir, las W deberían tener una gran masa. Por poseer un espín entero, las W serían bosones, y por ser éste distinto de cero, a las W se les conoce como bosones vectoriales intermediarios.
XII.5. SIMETRÍA ENTRE LOS CAMPOS DÉBIL Y ELECTROMAGNÉTICO
En 1958 John Ward y su alumno pakistaní Abdus Salam encontraron que, si la formulación que describe a la fuerza débil pertenece a la familia de las teorías de norma con simetría local, debería existir entonces un bosón intermediario con masa pero sin carga. Originalmente a esta partícula se le llamó X (por ser la letra que sigue de la W), aunque ahora se le denomina Z. Esta nueva partícula mediaría, por ejemplo, en la dispersión neutrón-neutrino, en la que no participa el campo electromagnético. Si hubiese una unificación entre estos dos campos, es decir si las fuerzas débil y electromagnética fueran sólo dos manifestaciones de una misma fuerza, la electro-débil, ¿a qué se debe que una de ellas tenga alcance infinito y la otra sólo se sienta a distancias nucleares? Dicho en otras palabras, ¿por qué el multiplete de mediadores del campo electrodébil contiene a la vez partículas con masa (las W y la Z) y sin masa (el fotón)?
Los primeros intentos por unificar las fuerzas débil y electromagnética se inspiraron en el intento fallido de unificar a la fuerte y a la electromagnética que había sido realizado por Yang y su colega Robert Lawrence Mills en 1954. Como se recordará, la fuerza fuerte es simétrica con respecto al intercambio de protones y neutrones; es decir que si se ignoran los efectos de la carga eléctrica del protón, un núcleo en el que se intercambien todos sus protones por neutrones y viceversa no sería distinguible del núcleo original. Esto indica una simetría global de norma. Una formulación completa de las interacciones fuertes debe considerar el caso más general de intercambios locales neutrón-protón. Como antes, la simetría global se pierde y para restablecerla localmente es necesario agregar algo. En este caso, sin embargo, es necesario suponer la existencia, no de una, sino de cuatro partículas sin masa. Dos de éstas, denominadas particulas de Yang-Mills, son neutras, y una de ellas podría identificarse con el fotón. Las dos restantes tienen la peculiaridad de poseer carga eléctrica, una positiva y otra negativa.
La teoría de Yang-Mills fue objetada casi de inmediato por varias razones fundamentales. Entre las más obvias estaba su predicción de la existencia de fotones cargados. Si hubiera partículas cargadas con masa inferior a la del electrón, el Universo sería totalmente distinto del que conocemos. Sin embargo, esta formulación posee algunas características matemáticas tan especiales que motivaron a los físicos teóricos a buscar alguna manera de modificarla para eliminar sus defectos más que a desecharla.
En la teoría de Yang-Mills, si se aplica una operación de simetría, llamémosla A, y luego otra B, el resultado es diferente de que se apliquen inversamente: primero B y luego A. Por esta razón, se dice que se trata de una teoría no-abeliana. Esta terminología se deriva del trabajo del matemático noruego Neils Henrik Abel, el cual a principios del siglo pasado estudió las propiedades de los grupos de transformaciones en las que se obtiene el mismo resultado si se conmutan. Uno de los mayores atractivos de las teorías de norma no-abelianas con simetría local es que la relatividad general pertenece a esta familia, por lo que una formulación de este tipo para cualquiera de las otras fuerzas sería un paso importante hacia la unificación.
XII.6. ROMPIMIENTO ESPONTÁNEO DE LA SIMETRÍA
La aparición de mediadores cargados y neutros en la teoría de Yang-Mills motivó a los interesados en la teoría del campo débil a buscar soluciones al problema de la falta de masa para los mediadores cargados. En 1964 el escocés Peter Ware Higgs encontró un método para dotar de masa a los campos de Yang-Mills sin romper la simetría local. La idea de Higgs se basa en un proceso conocido como rotura espontánea de simetría. Este mecanismo se puede ilustrar tomando como ejemplo una canica en el fondo de una botella de vino. Las botellas, en general, presentan simetría cilíndrica, por lo que la posición simétrica de la canica en el fondo sería el centro. Sin embargo los envases de vino se caracterizan por tener un bordo central en el fondo que obliga a una canica a permanecer en un estado asimétrico, en una orilla. En otros términos, el estado simétrico es de mayor energía potencial que el asimétrico. Si se deja a la canica sobre el bordo, por un instante habrá simetría pues la canica tendría libertad de caer en cualquier dirección. Sin embargo, cuando cae, hay un rompimiento espontáneo de la simetría, y la simetría queda escondida.
Según Higgs, refiriéndose a la masa de los campos de Yang-Mills, el estado simétrico corresponde al caso de campos sin masa; sin embargo, la existencia de un nuevo campo elevaría la energía de este estado por encima de otro en el que las partículas de Yang- Mills adquieren masa.
XII.7. UNIFICACIÓN ELECTRO-DÉBIL
En 1967 Steven Weinberg, por un lado, y Salam y Ward por otro, propusieron una teoría de interacciones débiles basada en una versión de la teoría de Yang-Mills según la cual tres de las partículas del campo correspondiente, una neutra y las otras dos cargadas, adquirían masa mediante un proceso de rompimiento espontáneo de la simetría. En este modelo, el campo de Higgs, responsable del rompimiento de simetría, introduce, a su vez, cuatro nuevas partículas, pero tres de ellas se mezclan con las partículas de Yang-Mills de manera que las dos cargadas y una de las neutras adquieren masa, y son identificadas con la W y la Z. La cuarta partícula de Yang-Mills, que es neutra, permanece sin masa, y resulta ser el fotón. De este nuevo arreglo sobra una partícula de Higgs que no se mezcla y, por lo tanto, queda como una predicción de la teoría. Había, sin embargo, algunos problemas serios por resolver. En cuanto a la teoría misma, había que probar que el modelo fuese renormalizable, en el mismo sentido en que Feynman y otros tuvieron que probar esto para la electrodinámica cuántica. Pero la mayor dificultad era experimental ya que, excepto por el fotón, ninguna de las otras partículas habían sido observadas.
En junio de 1971, el holandés Gerard't Hooft, entonces estudiante de doctorado, encontró una formulación sobre un rompimiento espontáneo de la simetría que es renormalizable. Este paso resolvió la dificultad teórica del modelo de Weinberg-Salam-Ward. El descubrimiento de Hooft causó gran revuelo entre los físicos de partículas y las propuestas experimentales para detectar bosones intermedios llovieron. Experimentalmente, las Z son más fáciles de identificar pues aparecen en situaciones en las que el campo electromagnético no juega ningún papel, tal como la dispersión de neutrinos por protones. En julio de 1973, en el CERN, F. J. Haert y sus colaboradores observaron las primeras evidencias de la dispersión de neutrinos por electrones, lo que puso en evidencia la existencia de las partículas Z.
La masa predicha para la Z y las W estaba entre 80 y 90 GeV, razón por la cual tuvieron que pasar diez años antes de que estas partículas pudieran ser producidas directamente en un laboratorio. Ésta fue la labor de Simón van der Meer y Carlo Rubbia. El primero desarrolló la técnica de aceleradores que hacía falta para observar colisiones de protones con antiprotones a más de 90 GeV. El segundo construyó un sistema de detección de más de 500 metros cúbicos llenos de cables y artefactos con un peso total superior a las 2 000 toneladas. Hacia enero de 1983, Rubbia anunció los resultados de sus primeros experimentos, en los que se observaron más de mil millones de eventos, seis de los cuales caían en la posición predicha para la masa de las W. El trabajo fue publicado por 135 coautores de catorce instituciones de investigación, la mayor parte de ellas europeas. En junio del mismo año, otra publicación del mismo grupo anunciaba los cinco primeros eventos en los que se identificaba una Z. Dos meses después ya eran ocho. En diciembre de 1984, Van der Meer y Rubbia recibían el último Premio Nobel en partículas elementales del periodo que cubre este libro.
La invariancia ante desplazamientos espaciales o temporales fue la primera forma de simetría que se encontró en las formulaciones físicas de Galileo y Newton. Otra simetría entre el magnetismo y la electricidad permitió a Faraday proponer su unificación, hace más de un siglo (sección XII.2). Una vez establecidas las formulaciones de los diferentes campos de fuerza que se conocen, aparecen simetrías que sugieren, también, una nueva unificación entre fuerzas (sección XII.3). En particular, Salam y otros encontraron que el campo débil (sección XII.4) acepta una formulación que es similar a la del electromagnetismo (sección XII.5). Una unificación de este estilo, sin embargo, debió encontrar una explicación a la enorme diferencia de alcances entre estas dos fuerzas (sección XII.6). La solución al problema fue propuesta por Weinberg, Salam y Ward (sección XII.7), quienes predijeron adecuadamente la masa de nuevas partículas que fueron descubiertas hace no mucho tiempo (sección XII.8).
