XI. LOS CUARKS: GELL-MANN Y ZWEIG
DEL gran volumen de datos acumulados hacia principios de la década
de 1960, comenzaron a hacerse evidentes ciertas regularidades interesantes.
Como se ha visto, las partículas podían ser clasificadas, según si eran o no
sensibles a la fuerza nuclear fuerte, en hadrones y leptones. Los hadrones más
ligeros son cientos de veces más pesados que el electrón, lo que podría indicar
alguna relación entre su masa y la magnitud de la fuerza que los gobierna. Además,
los hadrones aparecen en grupos. Por ejemplo, el neutrón y el protón, desde
el punto de vista de sus números cuánticos, son idénticos excepto por su carga
eléctrica y la ligera diferencia de sus masas. Esto fue tomado como indicación
de que podría tratarse de dos aspectos de una misma partícula: el nucleón.
A partir de entonces siguieron apareciendo familias de partículas de este tipo,
denominadas multipletes de carga, como los piones (3), las ñ
= (3) y las X (2). Otro hallazgo
notable fue el descubrimiento de todo un espectro de estados excitados
para varios de los hadrones. ¿Podría existir una subestructura?
Ya en 1949 Fermi y su alumno chino Chen Ning Yang, el mismo que predijo la violación de la paridad para los procesos débiles, habían sugerido la posibilidad de que los mesones no fueran elementales sino que estuvieran compuestos de pares nucleón-antinucleón. El descubrimiento de las partículas extrañas motivó luego al japonés Shoichi Sakata a extender estas ideas con la inclusión de la L como constituyente fundamental de los mesones. Se trataba entonces de encontrar una manera de asociar un par específico de estos bariones a cada mesón. Debido a las diferentes maneras de acoplar los números cuánticos, cada par barión-antibarión podía, según ellos, generar una variedad de mesones distintos. En 1959 los alumnos de Sakata, M. Ikeda, Y. Ohnuki y S. Ogawa, estudiaron este problema, encontrando que los tres hadrones, el triplete (n, p, L ), podían ser asociados a una configuración tridimensional de un grupo de transformaciones matemáticas denominado SU (3), y las respectivas antipartículas a otra configuración del mismo tipo.
Los fundamentos matemáticos de la teoría de grupos utilizada entonces fueron
desarrollados en el siglo XIX por el noruego Sophus Lie. Las siglas
SU (3) significan (grupo) unitario especial de matrices de 3 X 3 dimensiones.
En el caso de mesones de espín cero, el acoplamiento barión-antibarión estudiado
por los alumnos de Sakata permite nueve alternativas, ocho de las cuales forman
una familia u octete. Sakata y sus alumnos relacionaron a este octete
con el conjunto de los siete mesones entonces conocidos: los tres piones, los
cuatro mesones K , más una octava
partícula aún desconocida. Esta última, el mesón -h ,
fue descubierta dos años después.
El propósito de agrupar hadrones en multipletes era encontrar una simetría
mayor que permitiera descubrir relaciones más estrechas entre estas partículas.
Por ejemplo, la similitud entre la masa del protón y del neutrón puso de manifiesto
la idea de isospín. Este número cuántico distingue entre los dos estados
de carga del nucleón (protón o neutrón). Si la masa de p y n fuera
idéntica la simetría sería exacta; sin embargo, las fuerzas electromagnética
y débil alteran (o rompen) esta simetría separando las masas de los nucleones.
La separación, en este caso, es pequeña porque la fuerza responsable de la ruptura
es también pequeña comparada con la fuerza fuerte. Este mismo argumento permite
entender la ligera desviación entre las masas de los piones y también entre
los mesones K . La mayor separación
entre las masas de los piones y los mesones K
. se pensó, podría deberse al rompimiento de una simetría mayor asociada
a diferentes componentes de la fuerza nuclear fuerte.
A pesar de que la propuesta del triplete (n, p, L )
como componente fundamental pronto encontró objeciones serias, el juego de
las simetrías había empezado y varios investigadores comenzaron a tratar
de encontrar relaciones entre grupos de partículas. En 1961 el físico estadunidense
Murray Gell-Maun, el israelí Yuval Ne'eman, y otros, observaron que era posible
agrupar a los nucleones, las L las ñ
= y las X en otro octete (véase
figura 10). Uno de los éxitos de este método fue la predicción de una relación
entre las masas promedio de los miembros del octete de bariones: la masa del
nucleón más la masa de la X debe ser igual
a la mitad de la suma de la masa de la L más
un tercio de la masa de la ñ . Esta igualdad
se cumple con una precisión menjor al 1 %, lo que es de notarse si se toma en
cuenta que las relaciones de simetría eran casi una adivinanza, dada la gran
separación entre masas. Todo esto apoyaría, entonces, la idea de una ruptura
de la simetría mayor. Pronto se encontró que las resonancias de los bariones
también se agrupan en octetes. Si los bariones fueran partículas independientes
entre sí, cualquier similitud sería fortuita. Por lo tanto, las regularidades
observadas indicaban alguna relación íntima entre ellas.
 |
 |
 |
|
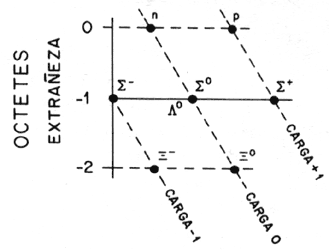
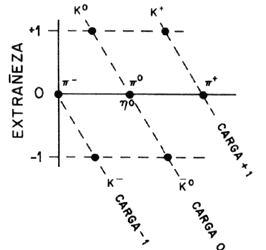
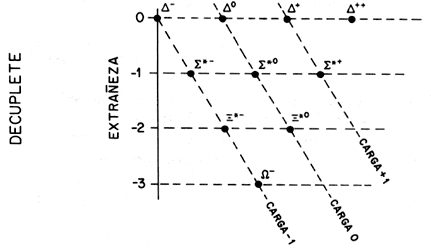
Figura 10. Múltiples hadrónicos. Sakata, Gell-Mann y Ne'eman encontraron
que al considerar la extrañeza y la carga eléctrica de los hadrones, éstos pueden
se agrupados según su masa en supermultipletes. Los bariones más ligeros
(arriba izquierda) y los mesones (arriba derecha) en octetes y los bariones
más pesados en un decuplete. Originalmente, dos huecos en estos diagramas (el
mesón h y la omega W-)
quedaron como predicciones cuya confirmación dio gran fuerza al modelo de los
cuarks.
Hacia fines de 1963, el juego de las simetrías no era la única línea de investigación para encontrar relaciones entre partículas elementales. Otras opciones incluían buscar correlaciones entre la masa de las partículas y su momento angular, en las llamadas trayectorias de Regge, en honor al físico italiano Tullio Regge, quien las introdujo por primera vez en 1959. Otros grupos buscaban explicar un modelo democrático, en el que, sin considerar a ninguna partícula como elemental, se postulara que estaban compuestas por diversas combinaciones de ellas mismas. Sin embargo, estas y otras ideas parecidas fueron cediendo terreno al modelo de simetrías en la medida en que éste fue teniendo mayor éxito.
En 1962, luego del descubrimiento de la primer resonancia X , Gell-Mann sugirió que esta partícula podía formar un decuplete, también predicho por SU (3), con los multipletes D y ñ. De ser así, debería existir un nuevo barión: la omega- W-. A principios de 1964, V. E. Barnes y su grupo observaron una partícula con las propiedades predichas por Gell-Mann. Quedaban, sin embargo, dos problemas evidentes: el SU (3) predice muchos más supermultipletes que los que observamos y, más importante aún, no existía una interpretación física que respaldase al modelo.
A principios de 1964, Gell-Mann y George Zweig, independientemente, hicieron notar que las simetrías observadas hasta entonces podían ser explicadas si se suponía la existencia de subpartículas, que Gell-Mann llamó cuarks, de las que estarían constituidos todos los hadrones. El modelo postula tres tipos (sabores) de cuarks: u, d y s (del inglés up, down y strange), que se agruparían por temas para formar bariones y por pares cuark-anticuark para formar mesones. Con estas reglas, se puede demostrar que sólo hay nueve combinaciones posibles cuark-anticuark para generar mesones y que éstas se agrupan en un octete más un singlete. En el caso de los bariones, hay 27 combinaciones de tres cuarks que se separan en un singlete, dos octetes y un decuplete. Estos supermultipletes coincidían exactamente con las familias observadas de hadrones.
El modelo de Gell-Mann y Zweig, sin embargo, mostraba un inconveniente: los cuarks deberían tener por carga eléctrica una fracción (1/3 para u y s, y 2/3 para d) de la carga del electrón. Partículas con esa propiedad deberían ser fáciles de identificar y, sin embargo, jamás se habían observado. ¿Se trataría, tan sólo, de una regla nemotécnica para reproducir lo observado, o habría una explicación física que respaldase tal modelo? Los experimentos para buscar cuarks proliferaron. Hasta la fecha, sin embargo, no existe evidencia convincente de su existencia como entes aislados. Quedaban, además, muchas preguntas pendientes; por ejemplo, era necesario explicar qué une a los cuarks, qué fuerzas son responsables de la estabilidad de los hadrones, qué previene que los cuarks se unan en grupos de cuatro o más, por qué los núcleos no colapsan en una sopa de cuarks.
Otra objeción que surgió de inmediato se relaciona con la estadística de los cuarks. Estas partículas deben tener espín semientero, es decir, son fermiones. Como tales, debido al principio de exclusión de Pauli, un barión no debería contener dos cuarks con los mismos números cuánticos. Sin embargo, en las reglas del modelo original de Gell-Mann para construir bariones, era necesario introducir dos, y hasta tres cuarks idénticos.
El mismo año en que apareció el modelo de los cuarks, Oscar Wallace Greenberg propuso que los cuarks no obedecen ni la estadística de Fermi, ni la de Bose, sino una paraestadística en que se permitía a tres cuarks idénticos ocupar un mismo estado. Una alternativa, aparentemente independiente, fue publicada por Moo-Young Han y Yoichiro Nambu en 1965. Ésta consistía en asociar a los cuarks una cualidad extra, parecida a la carga eléctrica, sólo que en tres variedades, que posteriormente se denominó color.
Según el modelo de Han y Nambu, existen tres colores, por ejemplo: rojo, amarillo y azul. Los cuarks están dotados de color (color positivo) y los anticuarks de anticolor (color negativo). La suma de un color con su anticolor, así como la suma de los tres colores, da como resultado partículas incoloras (color cero). Color y anticolor, así como colores distintos, se atraen. Colores o anticolores iguales se repelen. El resultado: los cuarks tienden a agruparse, ya sea por pares cuark-anticuark de un mismo color, formando mesones incoloros, ya sea por ternas de cuarks de diferentes colores, formando bariones incoloros. En resumen, el color de los hadrones es siempre cero. En 1966 Greenberg demostró que el modelo del color era equivalente a su modelo de la paraestadística, razón por la cual algunos autores atribuyen a Greenberg la introducción del color en la teoría de los cuarks.
El modelo del color resuelve elegantemente el problema de la estadística, ya que ninguno de los cuarks que forman un barión son idénticos, pues poseen distinto color. Los colores introducidos al formalismo de los grupos agregan una nueva representación de SU(3). La fuerza entre los cuarks es transmitida por los gluones (del inglés glue, pegamento). Los gluones intercambian el color de los cuarks. Con tres colores y tres anticolores se pueden lograr nueve combinaciones; sin embargo, una de ellas recibe contribuciones iguales de rojo combinado con antirrojo, azul con antiazul y amarillo con antiamarillo, lo que da por resultado una mezcla incolora. Las ocho combinaciones restantes generan el octete de gluones de color.
La introducción del color tiene como consecuencia multiplicar el número de cuarks por tres. Sin embargo, la condición de que los hadrones sean incoloros evita que aumente el número de hadrones predichos, pues todas las combinaciones de cuarks que contienen color diferente de cero se eliminan. Si bien la inclusión del color daba una salida al problema de la estadística, restaba elegancia al modelo original que parecía explicar el origen de más de ochenta hadrones conocidos entonces con base en sólo tres cuarks. Otra complicación era justificar las reglas de interacción entre los cuarks de colores, y dar una formulación para el campo gluónico.
El modelo de los cuarks siguió siendo visto con escepticismo hasta que en 1968 aparecieron las primeras evidencias experimentales directas sobre la existencia de una estructura interna para el protón. Siguiendo un criterio parecido al que usó Rutherford sesenta años antes para estudiar la distribución de carga en el átomo, un grupo de científicos norteamericanos guiados por Henry W. Kendall y Wolfgang K. H. Panofsky realizaron una serie de experimentos para determinar la distribución de carga dentro del protón. El experimento consistió en bombardear protones con electrones de muy alta energía.
El modelo de los cuarks sólo sugería la existencia de tres partículas dentro del nucleón. Se ignoraba cómo estaban ordenados dentro y la forma de la fuerza que los unía, si bien ésta debería ser lo suficientemente grande como para que jamás se hubiera visto un cuark libre. Con estas bases, se desarrolló una teoría de la dispersión de leptones por un conjunto de partículas altamente correlacionadas. Sin embargo, los resultados experimentales no concordaban con las predicciones. Poco tiempo después, el controvertido pero genial físico estadounidense Richard Phillips Feynman propuso un modelo alternativo.
Según Feynman, el leptón incidente ve al protón como una bolsa llena de partículas sin estructura, que él denominó partones, y que, con excepción de las paredes de la bolsa, se mueven libremente dentro del nucleón. Las predicciones del modelo de Feynman reproducían algunos aspectos importantes de los datos, pero quedaba por especificar qué eran los partones.
Los resultados anteriores despertaron gran interés entre las comunidades teóricas y experimentales. Pronto el grupo Kendall-Panofsky y otros en Europa utilizaron haces de muones y de neutrinos para estudiar el fenómeno. Como resultado se llegó a la conclusión de que los centros dispersores dentro del protón eran consistentes con partículas de espín 1/2 y carga eléctrica fraccionaria.
¿Qué eran los partones? La suposición de que se tratara simplemente de cuarks no ajustaba los datos experimentales. Se intentó agregar un mar de pares cuark-anticuark generado por el campo de atracción fuerte, con resultados igualmente negativos. Sólo al suponer la presencia de partículas neutras se logró ajustar los datos. Los gluones, como los fotones, son partículas neutras, sin masa y con espín 1, por lo que fue lógico suponer que eran éstas las partículas postuladas por el cálculo. Sin embargo había necesidad de una evidencia independiente sobre la existencia de color en los cuarks.
En ausencia de cuarks libres, la idea de color sólo podía comprobarse indirectamente comparando predicciones de modelos con y sin color. Un experimento de este tipo fue realizado en 1970 por un grupo del laboratorio de Frascati, cerca de Roma. Las colisiones entre electrones y positrones de gran velocidad disipan energía produciendo pares partícula-antipartícula (leptones y/o hadrones). La producción relativa entre pares de hadrones y, digamos, pares de muones depende de un coeficiente llamado R. A energías suficientemente altas, R. es simplemente la suma de los cuadrados de las cargas de todos los cuarks y todos los leptones. Suponiendo que sólo hay dos leptones cargados, el electrón y el muon, el valor medido de R. puede utilizarse para deducir el número de cuarks que existen. Por ejemplo, si sólo hay tres cuarks, R. debería valer 2/3, mientras que si hay nueve cuarks el resultado debería ser 2. El experimento de Frascati, medido a 1.5 GeV (1 GeV = 1 000 MeV), encontró que el parámetro R. era de 2.5, hecho que apoyaba fuertemente la teoría del color.
La confirmación de la existencia de cuarks de colores abría el camino para un enorme esfuerzo teórico por entender la dinámica caprichosa de estos objetos. Los cuarks, contra lo que se pensaba, parecen moverse libremente dentro de los hadrones, y sin embargo, no escapan. La solución a esta paradoja requirió una formulación cuántica de la teoría del campo gluónico: la cromodinámica cuántica (CC). Esta teoría es equivalente a la electrodinámica cuántica (EC), la cual explica el campo fotónico. En el caso de la EC, como se ha visto, la magnitud del campo electromagnético disminuye con el cuadrado de la distancia entre las cargas eléctricas. Esta ley presenta un problema serio cuando se trata de una partícula como el electrón que, supuestamente, carece de dimensiones. Si el electrón no tiene un radio finito, por ser puntual, el campo eléctrico que genera tiende a ser infinito en la medida en que nos acercamos a él.
El problema de los infinitos en EC, que causó ciertos dolores de cabeza al propio Dirac mientras desarrollaba la primera versión de esa teoría, fue resuelto por un método conocido como renormalización. Este consiste en suponer que, si bien el electrón no tiene dimensiones, la energía del campo se materializa produciendo un mar de pares (partícula-antipartícula) virtuales. La generación de estos pares es virtual en el sentido de que, al crearse, violan temporalmente el principio de conservación de la energía, solapadas por otro principio, el de la incertidumbre de Heisenberg, lo que garantiza que no pueden ser observadas directamente. Sin embargo, estas partículas se encargan de apantallar la carga eléctrica infinita que tendría un electrón desnudo (sin su mar de pares virtuales), disminuyendo el campo eléctrico que ésta genera. El número de pares aumenta con la distancia, y se reduce en la misma proporción el campo eléctrico, lo que da por resultado un campo equivalente al de una carga finita.
En el caso de la CC, los cuarks desnudos también están rodeados por un mar de pares cuark-anticuark virtuales que apantallan la carga de color. Sin embargo, a diferencia del caso de la EC, en la que los emisores del campo son neutros, en CC los gluones poseen una carga de color neta, diferente de cero. Esto tiene como consecuencia que, al aumentar el número de gluones con la distancia, la carga de color aumenta en la misma proporción. Es decir, la fuerza entre cuarks no disminuye con la distancia sino que aumenta. Esto, denominado confinamiento, evita que los cuarks escapen de los hadrones que los contienen.
El efecto neto es equivalente a imaginar que los hadrones estén compuestos por conjuntos de cuarks ligados por resortes. Mientras se mantienen juntos, la fuerza de los resortes es débil y se comportan como libres. Si se agrega energía, de manera que los cuarks tiendan a alejarse, la fuerza de atracción entre ellos aumenta por la acción de los resortes. Un cuark puede alejarse de un hadrón hasta el punto en que la energía de atracción del campo es equivalente a la masa de un par cuark-anticuark. Entonces, el resorte se rompe pero el cuark no queda libre, pues, por atracción de color, el anticuark recién creado se le une a través de un nuevo resorte, mientras que el nuevo cuark toma el lugar del cuark que se separó. En resumen, la predicción es que, tal como la evidencia experimental lo indica, los cuarks no pueden quedar aislados por mucho tiempo, y que al estar unidos en un hadrón se comportan casi como si estuvieran libres. El confinamiento gluónico da una explicación a la bolsa del modelo de partones de Feynman.
Desde el punto de vista de las cuatro fuerzas fundamentales, gravitacional, electromagnética, fuerte y débil, la aparición de los cuarks no agregó una más, sino que dio una explicación más básica a la fuerza fuerte. En este sentido, la fuerza nuclear fuerte que sienten los nucleones en el núcleo pasó a ser vista como una interacción efectiva externa, resultado de las interacciones entre cuarks. Esta situación se asemeja a la fuerza entre moléculas, denominada de Van der Waals, que es la expresión externa de la interacción electromagnética entre los electrones y el núcleo atómico.
Desde la postulación del modelo de los cuarks, en 1964, los norteamericanos
James Daniel Bjorken y Sheldom Lee Glashow propusieron la existencia de un cuarto
sabor para los cuarks: el encanto14![[Nota 15]](../imgs/mcommnt.gif){kind=small}
Con miras a una posible teoría unificada de las partículas elementales
se buscaban simetrías entre leptones y cuarks. Como se ha dicho, hasta
entonces se habían descubierto cuatro leptones (el electrón, el
muon, y sus respectivos neutrinos) y sólo tres sabores de cuarks (u,
d y s) ¿Habría un cuarto sabor? La sistemática observada en la
interacción de partículas, hacia 1967, también motivó a John Iliopoulos, Luciano
Maiani y al propio Glashow a insistir en la existencia de un cuarto sabor. Sin
embargo, estos argumentos aislados no eran suficientes para tomar en serio tal
hipótesis.
Desde 1970 las medidas del coeficiente R en la interacción entre leptones
fueron repetidas a energías cada vez mayores, a medida que los aceleradores
lo permitían. Como se mencionó, el valor de R debería tender a una
constante, a altas energías. En 1973, sin embargo, las medidas a 2 GeV dieron
un valor de R = 4.7 y, posteriormente, una medida a 2.5 GeV mostró un
valor de R = 6.0. De ser cierto, esto implicaría que las conclusiones
sobre el color de los cuarks eran prematuras. Intrigado por este fenómeno, en
el laboratorio SLAC de Stanford, Burton Richter y su grupo iniciaron
un programa de medidas sistemáticas de R, a intervalos de energías más
finos. En noviembre de 1974, descubrieron que el aumento en R se debía
a la presencia de una resonancia enorme y muy aguda localizada a 3.1 GeV, que
denominaron partícula Y . La interpretación
de este fenómeno requería, inequívocamente, la existencia del cuarto sabor.
Curiosamente, por la misma época, pero con una motivación diferente, Samuel
Ting y un grupo del Instituto Tecnológico de Massachussetts (MIT)
que trabajaba en el laboratorio de Brookhaven buscaban un nuevo mesón. Meses
antes que el grupo de SLAC, Ting había encontrado la misma resonancia
pero, cauteloso, repetía sus medidas para confirmar su hallazgo. Horas después
de enterarse del descubrimiento de Richter, el propio Ting anunció sus resultados
bautizando a su partícula como J. Esta discrepancia en nomenclaturas
dio como resultado que, en la actualidad, a esa resonancia se le conozca como
J/Y . Diez días después de este descubrimiento,
el grupo de SLAC encontró una nueva resonancia a 3.7 GeV, llamada Y
'.
La aparición de un nuevo tipo de cuark, más pesado, implicaba un aumento en el número de hadrones y resonancias hadrónicas. Las J/Y y Y ' son resonancias de cuark-anticuark encantados. En la actualidad se conocen nueve resonancias de este tipo. En junio de 1976 el grupo dirigido por Gerson Goldhaber anunció las primeras evidencias de bariones encantados neutros y, poco después, los primeros bariones cargados de este tipo. La espectroscopía de bariones encantados también se ajustó al postulado de un nuevo sabor. El encanto quedó establecido, aumentando así el número de cuarks a doce.
Como tantas otras veces, los cuatro leptones y los cuatro sabores de cuarks daban la impresión de haber llegado a una etapa de armonía, que sugería el fin del camino. Pero, como también es costumbre, este panorama habría de cambiar en pocos meses. Una vez resuelto el dilema de las resonancias encantadas, se podía extraer un valor estable para R. Con un nuevo cuark, cuya carga eléctrica resultó ser 2/3 de la del electrón, el valor previsible de R debería ser 3.3; sin embargo, el valor observado era cercano a 5.
En agosto de 1975, un grupo del SLAC dirigido por Martin Lewis
Perl reportó haber encontrado evidencias para la existencia de un nuevo leptón,
al que nombraron t (por ser el tercero).
Un nuevo miembro de la familia de leptones era bastante inesperado; sin embargo,
llegaba justo a tiempo para explicar la mayor parte de la discrepancia en el
valor de R, ya que la t tiene,
como el electrón y el muon, una carga eléctrica unitaria. El nuevo leptón es
casi cuatro mil veces más pesado que el electrón, o sea, tiene veinte veces
la masa del muon. Pero... ¿y la simetría entre el número de cuarks y el de leptones?
XI.11. LA "BELLEZA" Y LA "VERDAD"
Nuevamente, motivados por una posible simetría, Leon Max Lederman y su grupo
del Fermilab, cerca de Chicago, analizaron las predicciones para la masa
de un nuevo cuark. Llevando casi hasta el límite de capacidad a su acelerador,
en 1977 descubrieron una nueva resonancia que denominaron t.
Pocos meses después, al mejorar su resolución en energía, el mismo grupo descubrió
que se trataba de tres resonancias, y no sólo de una. Eran los primeros miembros
del espectro de resonancias de mesones asociados a un nuevo sabor de cuarks:
la belleza15
fue descubierta y dada a conocer por primera vez en 1980 por D. Andrews y su
grupo de la Universidad de Cornell.
El descubrimiento del leptón t sugiere
la existencia de un neutrino que lo acompañe. En tal caso, la famosa simetría
leptón-cuark implicaría un sexto sabor para los cuarks: la verdad16
Sin embargo, en los diez años posteriores al descubrimiento de la
t y la belleza, no se han podido encontrar evidencias experimentales
ni del nuevo neutrino ni de la verdad. En el primer caso, se puede deber a un
problema de estadística, ya que la producción de leptones t
dista mucho de concretarse en un haz lo suficientemente intenso como para estudiar
sus interacciones. En cuanto a los cuarks con verdad, se estima que su masa
debe ser superior a los 23 GeV, pero nadie sabe qué tanto. Por ello éste es
actualmente uno de los temas favoritos en las solicitudes de apoyo económico
para aumentar la energía de los aceleradores.
En lo descrito hasta ahora, el panorama de las partículas que hoy consideramos como verdaderamente elementales comienza, nuevamente, a verse sobrepoblado. El menú actual contiene casi sesenta partículas: cinco leptones, quince cuarks (cinco sabores de tres colores), ocho gluones, las antipartículas de todos éstos y además el fotón. Todo ello sin considerar partículas que aún no hemos discutido como las transmisoras del campo débil y del campo gravitatorio, además de la certeza sobre la existencia de, al menos, los sextos miembros de las familias de los cuarks y los leptones. ¿Estaremos en la víspera de una nueva síntesis?
Los primeros intentos por descubrir una subestructura para los hadrones se dieron en la década de 1950, años en los que se introdujeron las ideas matemáticas de grupos de simetrías (sección XI.2); luego de algunos fracasos, surgieron algunas regularidades que permitieron, incluso, predecir con éxito la existencia de nuevas partículas (sección XI.3). Gell-Mann, especie de Mendeleev moderno, pronto se dio cuenta de que un modelo simple, con base en tres partículas, los cuarks, explicaba gran parte de la fenomenología observada (sección XI.4). Pronto surgen algunas inconsistencias que requieren agregar al modelo una nueva cualidad: el color (sección XI.5). El escepticismo de muchos por los cuarks de colores se redujo al aparecer evidencias experimentales de una subestructura para el protón (sección XI.6). Con esto, la física teórica tuvo que desarrollar el formalismo que permitiese cálculos más cuantitativos: la cromodinámica cuántica (sección XI.7). Los primeros resultados de este esfuerzo permitieron explicar algunas incógnitas, como el confinamiento de los cuarks (sección XI.8). La armonía de esta teoría con la fenomenología de las interacciones débiles sugirió la existencia de un nuevo cuark: el encantado (sección XI.9). La aparición de nuevos leptones (sección XI.10) requirió más añadidos al modelo de los cuarks (sección XI. 11).
