DOS, CUATRO, OCHO... ñINFINITO!

La obra de Malthus sobre los principios de la población es muy compleja, y fue escrita en el seno de condiciones sociales y culturales muy particulares no solamente por la época, sino por el país en que se daban. Adicionalmente y como ocurre con toda obra que provoca controversias, en especial por las profundas implicaciones sociológicas que tiene, la obra de Malthus ha recibido innumerables ataques y críticas, algunas muy justificadas, pero otras distorsionadas e incluso incongruentes entre sí, ya sea por ignorancia o por razones ideológicas.

Un principio que sustenta gran parte del contenido del Ensayo sobre el principio de la población es el argumento en torno a las diferencias entre la forma en que las poblaciones crecen (Malthus siempre se refirió a poblaciones humanas) y la forma en que los recursos disponibles para ellas lo hacen. Malthus puntualizaba, muy acertadamente, que las poblaciones tienden a crecer en progresión exponencial (o "geométricamente", como él lo dice), mientras que los recursos (alimentos y otros elementos necesarios para la sobrevivencia del hombre) sólo pueden crecer linealmente, esto es, en una progresión aritmética.

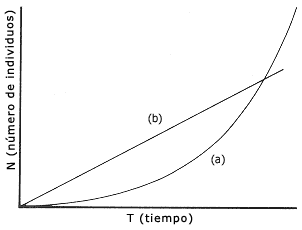
Una progresión exponencial o geométrica es aquella en que se multiplica la cantidad anterior a cada paso por un valor constante; por ejemplo 2, 4, 8, 16, 32, 64, etc., donde el sexto paso (64) representa una cantidad 32 veces mayor que el primero. Desde luego, la exponencial también puede ser una función decreciente en forma geométrica, alcanzando por ejemplo, la mitad del valor anterior a cada cambio de unidad de tiempo. Una progresión aritmética, por el contrario, se incrementa sumando la misma cantidad a cada paso, v.g., 2, 4, 6, 8, 10, 12, etc., donde el sexto paso (12) es, lógicamente, sólo seis veces mayor que el primero. De igual forma una función de cambio aritmético también puede ser decreciente. La figura 1 es una representación gráfica de estos dos tipos de progresiones o crecimientos: a) el exponencial o geométrico y b) el aritmético. De la diferencia de los valores alcanzados por cada una de las dos líneas de dicha figura resulta evidente que la progresión exponencial o geométrica se aleja cada vez más de la aritmética.

Con un poco de observación acerca del crecimiento de una población humana, Malthus, como cualquier otra persona, llegó a la conclusión de que la capacidad natural de crecimiento del hombre es exponencial, lo que no ocurre con la producción agrícola. 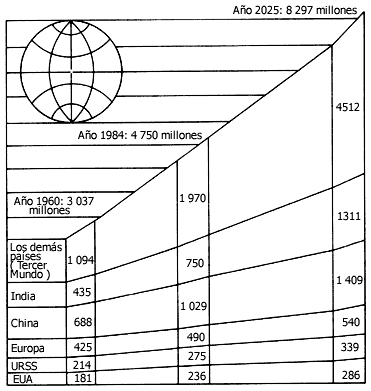Aunque Malthus no contaba con datos demográficos adecuados para corroborar su hipótesis, le bastaron unos sencillos cálculos matemáticos para predecir dicho crecimiento de la población. La figura 2 describe el crecimiento de la población mundial de 1960 a 2025, y representa una curva exponencial casi perfecta. Este tipo de curva se puede lograr también, en condiciones experimentales controladas, con microorganismos (por ejemplo bacterias o levaduras) que crecen en medios de cultivo sin restricciones. Sin embargo, la curva de crecimiento deja de ser exponencial conforme el medio de cultivo se satura con los microorganismos y los recursos nutritivos empiezan a no ser suficientes para todos los individuos presentes, o bien cuando éstos generan residuos metabólicos tóxicos que, al acumularse con el crecimiento de la colonia, limitan el ulterior crecimiento de la población. También se han observado curvas de este tipo para poblaciones de organismos superiores en condiciones naturales (plantas vasculares y vertebrados) que empiezan a colonizar un área originalmente desprovista de ellos, hasta que el área se satura de organismos y la población deja de crecer en tamaño y se estabiliza.

8

Figura 1. Contraste entre el crecimiento exponencial (a) y el crecimiento aritmético (b).

En resumen, todos los organismos, incluido el hombre, tienen un potencial de crecimiento poblacional exponencial. Sin embargo, hay diferentes factores del medio que impiden que dicho crecimiento se logre, por lo que las poblaciones se mantienen en tamaños de equilibrio más o menos fluctuantes. La única especie que hasta el momento presenta en forma sostenida un crecimiento de tipo exponencial de su población es la humana (Fig. 3).

8

Figura 2. Crecimiento de la población mundial global y para diferentes regiones del mundo.

8

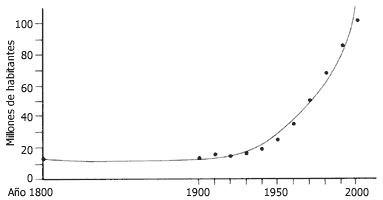
Figura 3. Curva de crecimiento de la población mexicana en un periodo de 200 años.

 

8 José Sarukhán, Introducción a la ecología de poblaciones. Un enfoque demográfico, México, Consejo Nacional para la Enseñanza de la Biología-Compañía Editorial Continental, 1987.