III. SIGNIFICADO DEL TIEMPO MEDIDO POR RADIACTIVIDAD
COMO mencionamos anteriormente, los sistemas de decaimiento m�s usualmente
utilizados en geolog�a son los siguientes:
| Potasio - arg�n |
| Rubidio - estroncio |
| Uranio - plomo |
| Torio - plomo |
�stos, desde luego, no son los �nicos, pues siendo la geocronolog�a un �rea activa de investigaci�n se desarrollan continuamente nuevos m�todos. Sin embargo los arriba mencionados son muy utilizados e ilustran con claridad los principios en que se basan los relojes radiactivos.
La primera determinaci�n de una edad geol�gica con este m�todo fue hecha por O. Hahn y sus colaboradores en 1943. Sin embargo, su uso se generaliz� s�lo hasta que el espectr�metro de masas y otras t�cnicas anal�ticas fueron perfeccionados a principios de los a�os cincuenta.
El rubidio (Rb) es un metal que por su radio at�mico parecido al del potasio (K) tiende a sustituirlo en las redes cristalinas que componen los minerales de las rocas. El potasio, a su vez, es un elemento importante en la composici�n de algunos minerales abundantes en las rocas de la corteza. Los minerales m�s importantes por su contenido de potasio son las micas, los feldespatos pot�sicos y los minerales que forman arcillas. La mica es familiar para nosotros pues se emplea en la fabricaci�n de resistencias el�ctricas; en las rocas �gneas aparece como peque�as laminillas muy brillantes. Los feldespatos tambi�n son muy comunes en las rocas �gneas de color claro como el granito. El rubidio tiene dos is�topos naturales, el Rb-85 y el Rb-87, y se ha calculado su abundancia natural como de 72.2 y 27.8% respectivamente.
El estroncio, por otra parte, tiene los siguientes cuatro is�topos estables naturales: Sr-88, Sr-87, Sr-86, y Sr-84, con una abundancia en la naturaleza de 82.5, 7.0, 9.9 y 0.6% respectivamente. Podemos ilustrar su decaimiento con la figura 7. En esta figura, un neutr�n del n�cleo de rubidio se transforma en prot�n, emitiendo un electr�n o part�cula beta negativa y un antineutrino y produciendo algo de calor. En forma simplificada, esto se escribe as�:
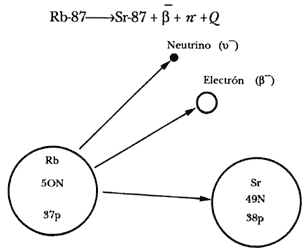
Figura 7. Esquema de decaimiento del rubidio-87.
Para calcular la edad de un mineral en que s�lo hubiera rubidio cuando se form�, solamente tendr�amos que saber la cantidad de Sr-87 presente y utilizar la ecuaci�n de decaimiento de la siguiente manera:
La cantidad de Sr-87 que hay en un momento determinado proviene del decaimiento de Rb-87, de manera que si restamos a la cantidad de Rb-87 que hab�a al principio, (Rb-87)o, la que hay en un momento dado, (Rb-87) t, obtenemos la cantidad de Sr-87 presente en ese momento:
En esta ecuaci�n, podemos sustituir el (Rb-87)o por medio de la ecuaci�n de decaimiento:
As� que la primera ecuaci�n nos da:
En esta ecuaci�n el tiempo transcurrido puede calcularse directamente si se conocen los valores de la constante de decaimiento y las concentraciones presentes de rubidio y estroncio. Sin embargo, existen dos hechos por los cuales no se emplea directamente. El primero de ellos consiste en que, cuando se form� el mineral y se convirti� en un sistema cerrado, ya hab�a probablemente alguna cantidad de estroncio presente. Esta contribuci�n hay que tomarla en cuenta en nuestros c�lculos o de lo contrario obtendr�amos valores err�neamente largos del tiempo. El Sr-87 ya presente en un principio, (Sr-87)o, puede ser tomado en cuenta a�adi�ndolo tan s�lo a la ecuaci�n:
Esta ecuaci�n podr�a aplicarse de manera directa para calcular el tiempo si conoci�ramos la concentraci�n original de estroncio en el mineral. Este dato no puede sino estimarse con cierto grado de incertidumbre; como las cantidades de Rb son s�lo de unos cuantos cientos de partes por mill�n, una peque�a incertidumbre en este valor introduce un error grande en el tiempo calculado. Para evitar esto se recurre a una t�cnica ingeniosa, que consiste en dividir los t�rminos de la ecuaci�n entre la concentraci�n de Sr original. Este is�topo es estable y no proviene de la descomposici�n de otro n�cleo radiactivo y por lo tanto su abundancia ha permanecido constante. Si hacemos esto tenemos:
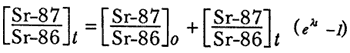
en donde se ha colocado el Sr-86 dentro de los par�ntesis porque, como hemos dicho, suponer que:
es razonable y no introduce un error significativo. Por otro lado, al tomarse cocientes el error se minimiza puesto que el Sr-86 existe en cantidades del mismo orden de magnitud que el Sr-87 y el Rb-87.
Ahora bien, si nos fijamos en la ecuaci�n final anterior y hacemos el siguiente cambio:
es decir, la ecuaci�n de una recta con intersecci�n en Yo y pendiente m (Figura 8).
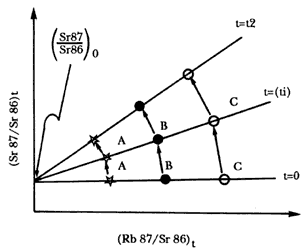
Figura 8. Evoluci�n de las is�cronas del estroncio. Los puntos A, B, C son valores dados por diferentes minerales cuyo contenido inicial de rubidio-87 es diferente.
Ahora bien, para un mineral dado, la determinaci�n de las razones de estroncio 87 y rubidio 87 a estroncio 86, fijan un punto sobre la recta, por ejemplo A en la figura 8. Si aplicamos este m�todo a varios minerales de una misma roca obtendremos varios puntos que definen la recta y podemos as� determinar tanto su pendiente, y por lo tanto el tiempo, como las razones originales de Sr-87/Sr-86. Para que los diferentes minerales definan una recta es necesario que hayan cristalizado al mismo tiempo. Se dice entonces que tienen edades concordantes; si esto no ocurre las edades son discordantes.
La recta definida por minerales de edad concordante es llamada is�crona y se caracteriza por su pendiente que aumenta con el tiempo.
Con respecto a la constante de decaimiento del rubidio se conoce ahora con la suficiente precisi�n para estimar tiempos del orden de miles de millones de a�os. Su valor es de:
El tiempo calculado con este procedimiento nos da la edad de una roca desde que �sta se convirti� en un sistema cerrado al intercambio isot�pico. Por este motivo, para las rocas �gneas, que provienen de la cristalizaci�n de un magma, la edad que se calcula es la que transcurri� desde su cristalizaci�n.
Sin embargo, las rocas pueden sufrir transformaciones posteriores por efectos de las altas presiones y temperaturas a que pueden estar sometidas. En estas condiciones, se llevan a cabo reacciones internas que producen cambios en las caracter�sticas f�sicas y cristalogr�ficas de los minerales o en la cristalizaci�n de minerales nuevos. Este proceso, llamado metamorfismo, permite abrir el sistema y cerrarlo nuevamente; esto es, durante el metamorfismo los minerales redistribuyen sus concentraciones de rubidio y estroncio y vuelven a quedar cerrados al intercambio de is�topos al t�rmino del mismo. La edad para este tipo de rocas es entonces la transcurrida desde su �ltima metamorfizaci�n.
Un proceso semejante al descrito puede seguirse para estudiar la edad de una unidad litol�gica, por ejemplo un macizo gran�tico. En este caso se pueden estudiar las razones de rubidio y estroncio no en minerales aislados sino en rocas completas de diferentes zonas del macizo. En este caso nuestro sistema cerrado es toda la formaci�n, y as�, estaremos estimando la edad desde que �sta cristaliz�. Si se combinan ambos m�todos se puede saber la edad de cristalizaci�n original, y la edad de cada uno de los procesos metam�rficos que la roca ha sufrido.
Por la vida media tan larga que tiene el rubidio y porque es poco abundante en rocas, las edades determinadas con este reloj se vuelven m�s confiables mientras m�s vieja es la roca, por ejemplo, si su edad es del orden de varios cientos de millones de a�os hasta miles de millones de a�os.
El reloj de potasio-arg�n se basa en el decaimiento del potasio 40 en el elemento estable arg�n 40. El potasio 40 no s�lo decae hacia este �ltimo elemento sino tambi�n hacia el calcio 40, como puede verse en el siguiente diagrama:
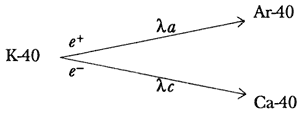
Podemos escribir, deriv�ndola en forma similar al caso Rb-Sr, la siguiente ecuaci�n:
en donde la constante de decaimiento es la suma de las dos constantes que describen la conversi�n hacia arg�n y hacia calcio:
Los valores de las constantes son:
Ahora bien, dada una cantidad inicial de K-40, la cantidad de �tomos que decaen en Ar-40 est� dada por:
de manera que podemos escribir la ecuaci�n de decaimiento como:
Si se despeja el tiempo en esta ecuaci�n se tiene:
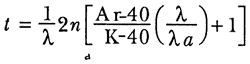
que es el tiempo transcurrido desde que empez� a acumularse el arg�n de tipo radiog�nico.
El arg�n es un gas noble que no se combina con los �tomos de los arreglos cristalinos que forman el mineral. Por esta raz�n el arg�n puede perderse f�cilmente cuando el mineral sufre metamorfismo. As�, el reloj de potasio-arg�n nos proporciona la edad del �ltimo proceso de cristalizaci�n de un mineral. Esto es, la edad de cristalizaci�n de una roca �gnea o de metamorfismo en una roca metam�rfica.
Dada la vida media del potasio 40, las edades que pueden ser obtenidas con este reloj son del orden de cientos de millones de a�os.
Relojes de uranio-plomo y torio-plomo
Otros tres elementos cuyo decaimiento es utilizado en la estimaci�n de edades y que generalmente son estudiados en conjunto por ser muy parecidos en su comportamiento son el uranio 238, el uranio 235 y el torio 232 (U-238, U-235, Th-232).
Estos elementos decaen a trav�s de una serie compleja a los productos estables plomo 206, plomo 207 y plomo 208 (Pb-206, P-207, Pb-208) respectivamente. A las series del U-238, U-235, y Th-232 se les llama serie del uranio, del actinio y del torio respectivamente. A las del U-235 y U-238 se les llama as� porque uno de los productos en la serie del primero es el U-234 y en la del segundo (U-238) es el actinio.
Como en estas series las constantes de decaimiento son sucesivamente mayores, se alcanza, como ya vimos, el equilibrio secular y podemos entonces representar el decaimiento de la siguiente forma:
Las constantes de decaimiento se han determinado y son las siguientes:
|
|
|
|
|
|
|
|
|
|
|
|
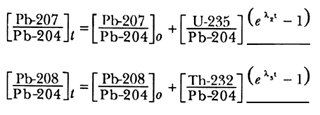
Ahora bien, existe un cuarto is�topo del plomo, el Pb-204 del que se sabe que decae a Mercurio 200 con una vida media tan larga (1.4 x 1017 a�os) que pr�cticamente puede tomarse como constante. As�, empleando la misma t�cnica seguida con el reloj de rubidio-estroncio podemos obtener tres relojes independientes:
|
|
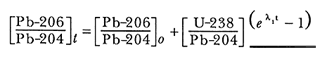
Podemos escribir esto m�s brevemente si tomamos en cuenta que la diferencia entre (Pb-206)t y (Pb-206)o, es decir entre el plomo actual y el que se encontraba desde que la roca o mineral se volvi� un sistema cerrado, es de origen radiactivo y puede denotarse por medio de un asterisco:
de manera que tendremos ecuaciones como:
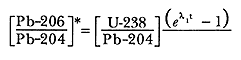
y similarmente para las otras series:
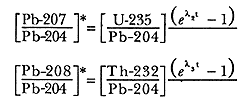
En estas ecuaciones, el tiempo se determina con diferentes elementos, de manera que pueden obtenerse valores independientes del tiempo transcurrido en un mismo mineral. Cuando las edades que dan dos o tres de estos m�todos independientes concuerdan dentro de un margen de error experimental, se dice que las edades son concordantes. Las edades pueden ser discordantes, es decir diferentes, si los minerales han sufrido p�rdida de plomo. En numerosos an�lisis los investigadores han encontrado con mucha frecuencia edades discordantes. Esto es debido probablemente a que los �tomos de plomo, por sus caracter�sticas f�sicas y radio at�mico, no quedan fijos en las redes cristalinas y se mueven con lentitud fuera del mineral.
Por medio de las relaciones anteriores es posible desarrollar un cuarto m�todo que aunque no es independiente est� libre del efecto de p�rdida de plomo:
Si tomamos las primeras dos ecuaciones dividimos la segunda entre la primera tendremos:
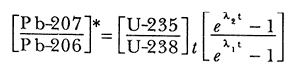
�sta es una ecuaci�n muy interesante porque relaciona el tiempo con el cociente de los plomos radiog�nicos (Pb-207/ Pb-206), y aun en el caso de que un mineral pierda plomo, perder� tanto de Pb-207 como de Pb-206 de tal manera que su cociente cambia muy poco. Adem�s, en la ecuaci�n anterior tambi�n interviene el cociente (U-235/U-238), es decir, la cantidad que hay en la Tierra actualmente de U-235 a U-238. Este valor es constante e igual a 1/137.8
Como veremos despu�s, el valor anterior es muy importante, de manera que lo vamos a repetir:
 |
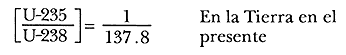Por lo tanto, la ecuaci�n del tiempo se simplifica a:
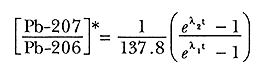
en donde s�lo tenemos dos variables que son el cociente de plomos (Pb-207/Pb-206) y el tiempo (recordemos que l1 y l2 son conocidas). La f�rmula anterior parece menos complicada si se grafica tal como se ilustra en la figura 9.
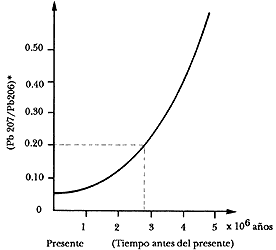
Figura 9. Evoluci�n del plomo de origen radiactivo (radiog�nico).
La gr�fica anterior es muy clara y permite relacionar r�pidamente la concentraci�n de plomo en un mineral con su edad. Por ejemplo, si un mineral tiene una relaci�n de plomo 207 a plomo 206 de 0.2, su edad es de 3 000 millones de a�os aproximadamente.
Entre los minerales que se suelen emplear muy a menudo para la determinaci�n de edad por el m�todo del plomo se encuentra el zirc�n, un mineral frecuente en las rocas �gneas y metam�rficas y que cuando es de buen tama�o y pureza se utiliza en joyer�a.
