I. SOMBRAS Y TAJADAS
PIENSE usted en un s�lido; una papa suspendida en el espacio es, por ejemplo, una buena imagen. Suponga que por alguna raz�n usted tiene informaci�n acerca de esta papa s�lo a trav�s de sus secciones transversales. Es decir, usted s�lo conoce la forma que tienen las tajadas de esta papa. Suponga ahora que quiz� usted conoce, de este s�lido, la forma que tienen las figuras que se obtienen al proyectarlo; es decir, imag�nese que de �l usted s�lo ha visto las sombras que deja sobre el piso. �Podr�a usted decirme, a partir de esta informaci�n, qu� forma tiene este s�lido?
La situaci�n es mucho menos rara de lo que uno se imagina. S�lo para mencionar dos ejemplos sumamente sencillos piense usted que, con frecuencia, cuando se usa el microscopio, lo que uno ve no es el objeto a observar, sino s�lo una tajada que de �l se obtuvo al hacer la preparaci�n; o que la informaci�n que nos llega de la forma de un cuerpo celeste, a trav�s de un telescopio, s�lo tiene que ver con las proyecciones de este cuerpo.
En este primer cap�tulo vamos a proponernos resolver quiz�s el aspecto m�s te�rico y sencillo de este problema. Quisi�ramos estudiar s�lidos que tienen siempre tajadas o sombras circulares y concluir, por supuesto, que estos s�lidos tienen la forma esf�rica. A trav�s de este libro vamos a vernos con frecuencia en la necesidad de concluir que determinado s�lido es una esfera, pues sus sombras o sus tajadas son circulares.
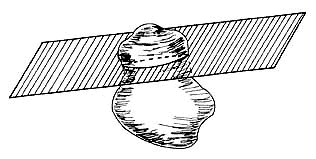
Debemos de estar seguros de que lo que ambos —usted, lector, y yo— entendemos por secci�n transversal o tajada es lo mismo. Volviendo a nuestra imagen de una papa suspendida en el espacio, imaginemos que un plano la corta (Figura I.1). Una tajada de esta papa o mejor dicho, una secci�n transversal de este s�lido, no es sino la parte de esta papa o de este s�lido que queda sobre el plano.
Antes de continuar quisiera aclarar otro concepto. A diferencia de otros autores, entendemos por un c�rculo o una esfera no s�lo el borde de �stos, sino tambi�n todo lo que se encuentra dentro de ellos. As�, por ejemplo, el centro del c�rculo forma parte del c�rculo.
Vamos a empezar pensando en secciones transversales o tajadas.
Si toda secci�n transversal de un s�lido Q es un c�rculo, entonces Q es una esfera.
Es decir: si en una papa toda tajada es circular, es porque la papa es una papa esf�rica.
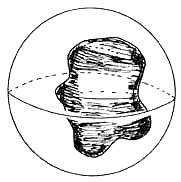
Demostraci�n. La esfera m�s peque�a que contiene al s�lido Q es llamada la circumesfera de Q. Su c�scara debe tocar al s�lido Q, puesto que si no lo toca �sta no ser�a la esfera m�s peque�a que contiene a Q (v�ase Figura I.2).
De hecho, la c�scara de la circumesfera debe tocar al s�lido Q en al menos dos puntos; de lo contrario, si solamente lo toca en un punto, despeg�ndola ser�a posible encontrar una esfera m�s peque�a que contenga a Q (Figura I.3).
Fijemos nuestra atenci�n en dos puntos de la c�scara de la circumesfera de Q que se encuentren tambi�n en Q. Pong�mosles nombre; llam�mosles por ejemplo X y Y. A continuaci�n haremos ver que cualquier otro punto de la c�scara de la circumesfera pertenece tambi�n a Q, mostrando as� que Q y su circumesfera coinciden.
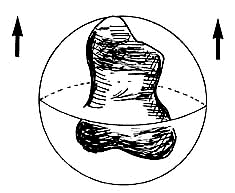
Manos a la obra: fij�monos en cualquier punto de la c�scara de la circumesfera de Q (escoja uno, el que usted quiera). Pong�mosle por nombre Z (ver figura I.4). En este momento conviene pensar que la circumesfera es azul y el s�lido Q es rojo (recuerde que para ayudarnos a pensar se vale hacer uso de cualquier truco, artima�a o man�a, lo importante es pensar).
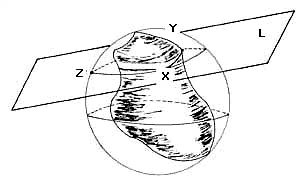
Pensemos ahora en el plano L que pasa por X, por Y y por Z. Este plano corta a la circumesfera en un c�rculo azul (toda tajada de una esfera es un c�rculo) que contiene a X, a Yy a Z en su orilla. A su vez, este plano corta al s�lido Q en un c�rculo rojo que contiene a X y a Y en su orilla y que se encuentra dentro del c�rculo azul, pues el s�lido e est� dentro de la circumesfera.
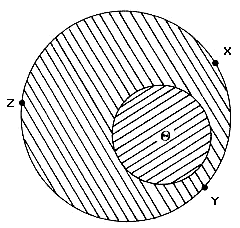
A continuaci�n, trate de dibujar un c�rculo rojo dentro de un c�rculo azul de tal forma que ambos compartan al menos dos puntos, X y Y, de su orilla (ver figura 1.5). Le ser� f�cil convencerse de que la �nica posibilidad es que ambos c�rculos, el rojo y el azul, coincidan. Esto quiere decir que la tajada de Q y la tajada de la circumesfera, determinadas ambas por el plano L, coinciden y, por lo tanto, que el punto Z de la c�scara de la circumesfera, en el cual hab�amos fijado nuestra atenci�n (ese que usted escogi� arbitrariamente), es parte del s�lido Q. Ahora podemos fijar nuestra atenci�n en cualquier otro punto de la c�scara de la circumesfera de Q y repetir el mismo proceso anterior para convencernos de que este punto, y por lo tanto cualquier otro de la c�scara de la circumesfera, es parte del s�lido Q. Hemos pues demostrado que el s�lido Q y su circumesfera coinciden, es decir, que el s�lido es esf�rico.
Pong�monos de acuerdo en lo que significa la proyecci�n o sombra de un s�lido. La idea intuitiva se refiere a la sombra que deja un s�lido sobre el piso, producida por los rayos del sol.
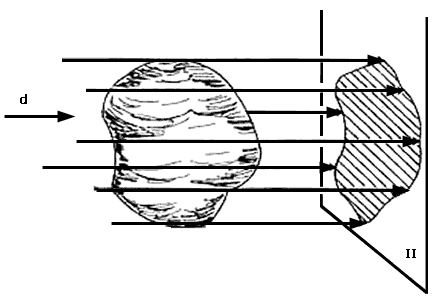
Tomemos una direcci�n d y un plano P perpendicular a esta direcci�n. Nos vamos a fijar en todas las posibles l�neas paralelas a la direcci�n d que cortan al s�lido (v�ase figura 1.6). Todas estas l�neas van a cortar tambi�n a el plano P para formar en �l una figura, que es la figura a la que llamaremos la proyecci�n o sombra del s�lido en la direcci�n d sobre el plano P.
Si toda proyecci�n de un s�lido Q es un c�rculo, entonces Q es una esfera.
Es decir: si todas las sombras de una papa son circulares, es porque la papa es una papa esf�rica.
Demostraci�n. Tomemos un s�lido Q con la propiedad de que todas sus sombras o proyecciones son circulares. Pudiera ser �por qu� no? que en diferentes direcciones las sombras tuvieran diferentes di�metros, es decir, que algunas sombras fueran m�s peque�as que otras. Empezaremos convenci�ndonos de que no es as�, de que en todas las direcciones las sombras son c�rculos del mismo tama�o.
Escoja usted dos planos. En ellos vamos a proyectar el s�lido Q y a verificar si ambas sombras tienen el mismo di�metro. Sean pues P y G los planos elegidos y sean P(Q ) y G(Q) los c�rculos que se obtienen al proyectar Q sobre P y G respectivamente (v�ase figura I.7).
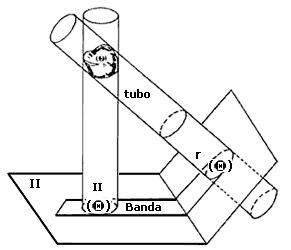
El cilindro generado por la sombra que deja Q al ser proyectado sobre el plano G es un tubo que perfora perpendicularmente a G precisamente en el c�rculo G(Q ). Este tubo se proyecta sobre P dejando como sombra una banda que aprisiona perfectamente al c�rculo P(Q). Por lo tanto, el di�metro de P(Q) es el ancho de la banda que, por ser la banda sombra del tubo, es el di�metro del tubo que a su vez no es otro sino el di�metro de P (Q).
Nos hemos convencido ya de que todas las sombras del s�lido Q son c�rculos del mismo di�metro. Ahora vamos a convencernos de que, efectivamente, el s�lido Q es una esfera. Con tal prop�sito vamos a pensar de nuevo en la circumesfera de Q, es decir, en la esfera m�s peque�a que contiene a Q. Conviene imaginar de nuevo que la circumesfera es azul, que el s�lido Q es rojo y que, en cualquier direcci�n que se tome, la sombra que proyecta el s�lido Q y su circumesfera es un c�rculo rojo dentro de un c�rculo azul. Recordemos que todas las sombras de Q son c�rculos rojos del mismo di�metro que se encuentran contenidos en las sombras de la circumesfera, las cuales son c�rculos azules todos del mismo di�metro. Por tanto, si en alguna direcci�n nosotros fu�ramos capaces de comprobar que el c�rculo rojo y el azul coinciden, entonces, en cualquier otra direcci�n, la sombra del s�lido y la sombra de su circumesfera coincidir�n.
Nuestro prop�sito inmediato es ahora verificar que, efectivamente, la aseveraci�n anterior es cierta, es decir, que las sombras de Q y de su circumesfera coinciden. Lo haremos encontrando simplemente, una direcci�n en la que las sombras proyectadas por el s�lido Q y su circumesfera coincidan.
Sean X y Y dos puntos de la c�scara de la circumesfera que sean parte del s�lido Q. Pensemos en el plano L determinado por los puntos X y Y y el centro de la circumesfera. Si proyectamos sobre un plano paralelo al plano L, lo que obtenemos es un c�rculo rojo dentro de un c�rculo azul en donde las proyecciones de los puntos X y Y se encuentran en la orilla del c�rculo azul. Por ser X y Y parte del s�lido Q, los c�rculos rojo y azul comparten dos puntos de su orilla. Como ya lo hab�amos constatado anteriormente, esto no es posible a menos que ambos c�rculos coincidan totalmente.
Hasta ahora todo lo que sabemos es que en cualquier direcci�n el s�lido Q y su circumesfera proyectan la misma sombra. �Ser� esto suficiente para asegurar que Q es una esfera? Si lo es, como lo veremos a continuaci�n.
Tome usted un punto de la c�scara de la circumesfera. �Cu�l? Cualquiera, el que usted elija arbitrariamente. Llam�moslo Z. Lo que quisi�ramos es convencemos de que Z es parte de Q. Para esto vamos a proyectar la circumesfera sobre un plano paralelo a un plano que pase por Z y el centro de la circumesfera. Al proyectar, la sombra de Z (llam�mosla Z') est� en la orilla de la sombra de la circumesfera. M�s a�n, de todos los puntos de la circumesfera, el �nico que se proyecta sobre Z' es Z, de manera que si Z no fuera parte del s�lido Q, entonces Z' no ser�a parte de la sombra de Q, lo cual no es posible pues sabemos que las sombras de Q y su circumesfera coinciden. Por lo tanto, forzosamente, Z debe formar parte de Q (v�ase figura I.8). Como Z fue escogido arbitrariamente, lo mismo pudimos haber concluido de cualquier otro punto de la c�scara de la circumesfera. Es decir, toda la c�scara de la circumesfera de Q forma parte de Q, lo cual nos indica que Q es una esfera.
Hemos terminado el primer cap�tulo de este libro. El siguiente cap�tulo es una introducci�n a la teor�a geom�trica de la convexidad, sin la cual mucho del material tratado en esta obra ser�a dif�cil de exponer. Por tanto, aunque el material presentado a continuaci�n aparentemente no se relaciona con lo que hasta aqu� hemos visto, nos ser� de mucha utilidad en los cap�tulos subsecuentes. Por otro lado, la teor�a geom�trica de la convexidad, por su sencillez y profundidad, es en s� misma de gran belleza y calidez. No dudo que su lectura le ser� muy estimulante y entretenida.
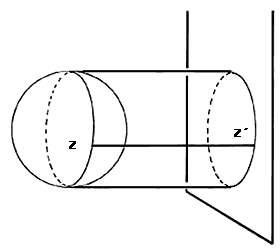
Figura I.8
