II. CONVEXIDAD
DECIMOS que una figura es convexa si cada vez que tomamos dos puntos en ella, el segmento que los une pertenece también a dicha figura.
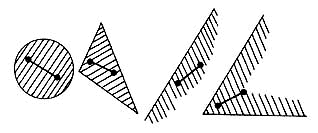
Así, por ejemplo, son figuras convexas un círculo, un semicírculo, una elipse, un paralelogramo, un triángulo, un segmento, un semiplano o un cono (véase figura II.1).
Una forma de construir más ejemplos es tomar varias figuras convexas y fijarse en la parte común a todas ellas. Si tomamos dos puntos que estén en la parte común, dado que las figuras son convexas, el segmento que los une estará en cada una de ellas y por tanto en la parte común a todas ellas. Esto es, la intersección, o parte común, de varias figuras convexas es una figura convexa (véase figura II.2).
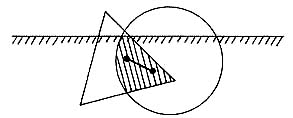
Intuitivamente, una figura es convexa si no está "abollada". Imagínese usted alguna figura "abollada". Notará que es precisamente en la abolladura donde es posible encontrar un segmento cuyos extremos estén en la figura pero que, sin embargo, debido a la abolladura, parte de él se salga de aquélla (véase la figura II.3).
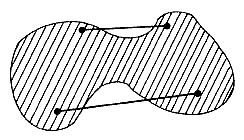
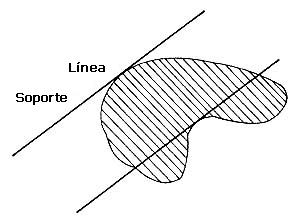
Es más, por aquellos puntos del borde de la figura en donde intuitivamente sentimos que ésta se encuentra abollada, es imposible trazar una línea que no parta a la figura en varios pedazos. En cambio, hay puntos del borde o frontera de la figura —en donde ésta no se halla abollada— por donde es posible trazar una línea que deje a la figura completamente de un lado (véase figura II.4).
Démosle nombre a este tipo de líneas: A una línea que toca a una figura y que la deja totalmente contenida en uno de los dos semiplanos determinados por ella, la llamaremos línea soporte de la figura. Siendo fieles a nuestra idea intuitiva de lo que sentimos que es una figura no abollada, se antoja decir que una figura es convexa si por cada punto de su frontera pasa una línea soporte. En efecto, veremos más adelante que así es. Por ahora, para seguir avanzando, es importante que aclaremos algunos conceptos de topología, como son el de interior y frontera de una figura.
Observando una figura podemos distinguir tres clases distintas de puntos: los puntos interiores, los puntos frontera y los puntos exteriores.
Un punto es un punto interior de una figura si podemos encontrar, alrededor de él, una pequeña bolita totalmente contenida en la figura. Por supuesto, entre más cerca del borde esté el punto, más chiquita será la bolita. Un punto es un punto frontera de una figura si cualquier bolita alrededor de él, por más chiquita que sea, tiene puntos que son de la figura y tiene puntos que no son de la figura. Si un punto de la figura no es interior, entonces cualquier bolita alrededor de él no está totalmente contenida en la figura y por lo tanto este punto tendrá que ser un punto frontera. Así, un punto de la figura, o es interior o es frontera, pero nunca ambas cosas a la vez. Intuitivamente consideramos que el borde de la figura está constituido por todos los puntos frontera. Finalmente tenemos a los puntos exteriores, que son aquellos alrededor de los cuales existe una pequeña bolita totalmente fuera de la figura. En una figura, los puntos exteriores son precisamente los puntos que no pertenecen a la figura. En la figura II.5 los puntos A y B son interiores, los puntos C y D son frontera, el punto E es exterior y q no es una bolita alrededor del punto F.
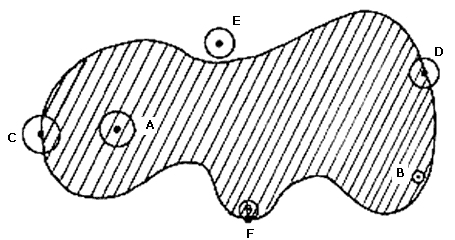
Demostración. Desde E empezamos a caminar hacia A sobre el segmento EA y paramos la primera vez que tocamos a la figura q . Llamémosle C a este punto. Si C fuera un punto interior habríamos tocado a q antes de llegar a C, pues existe una bolita, alrededor de C, totalmente contenida en q. Por otro lado, si C fuera un punto exterior, entonces al llegar a C, aún no habríamos tocado a q. Como no es interior ni exterior, C tiene que ser un punto frontera.
Entre dos puntos interiores A y B, de una figura convexa q todos los puntos son puntos interiores.
Demostración. Como en otras ocasiones, conviene pensar que q es de color rojo. Alrededor de A y de B existen bolitas de color rojo. Como Q es convexa, todos los posibles segmentos que unen a puntos de estas dos bolitas son de color rojo. Si ilumináramos todos estos posibles segmentos de rojo veríamos que alrededor de cualquier punto del segmento AB existe una pequeña bolita roja (véase figura II.6).
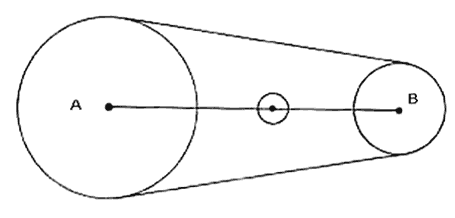
Demostración. La demostración es idéntica a la anterior. Pensemos que
q es roja. Alrededor de A existe una bolita
roja a la que llamaremos Q. Como todos los
segmentos que unen el punto B con algún punto de q
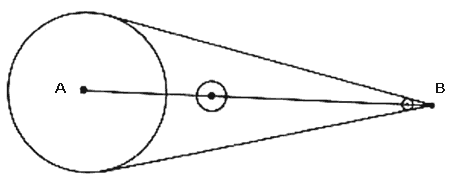
son rojos, entonces existe un barquillo rojo, que empieza en B y cuya
nieve es q (ver figura II.7). Por lo tanto,
alrededor de cualquier punto del segmento AB, distinto del punto B,
existe una bolita roja. Fíjese que entre más cerca de B tomemos al punto,
más chiquita tendremos que escoger la bolita roja alrededor de él. ![]()
Entre dos puntos frontera A y B de una figura convexa o todos los puntos son frontera o todos los puntos son interiores.
Demostración. Si todos los puntos del segmento AB son puntos frontera, hemos acabado. Si no, quiere decir que, entre A y B, existe un punto interior. Llamémoslo C. Luego, entre C y A, y entre C y B sólo tenemos puntos interiores. Esto es, basta con que haya un punto interior entre A y B, para que todos sean interiores.
Existen figuras, como una línea, un semiplano o un cono, que se extienden hacia el infinito. Las demás, aquellas que no se extienden hacia el infinito y que por lo tanto están totalmente contenidas dentro de un círculo suficientemente grande, serán llamadas figuras acotadas.
A continuación hablaremos sobre una propiedad de las figuras convexas acotadas, que será muy usada en lo sucesivo.
Si una línea L pasa por un punto interior A de una figura convexa acotada q entonces L corta a la frontera de q en exactamente dos puntos. (Ver figura II.8).
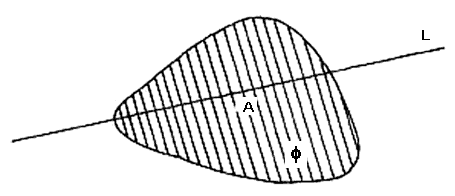
Demostración. Ya que F es acotada,
muy lejos, sobre la línea L a la izquierda de A, hay un punto
que no pertenece a F. Entre este punto y el
punto A debe de haber un punto frontera de F.
Por otro lado, como entre un punto interior y un punto frontera sólo hay puntos
interiores, sobre L a la izquierda de A, no puede haber dos puntos
frontera. Esto es, sobre L a la izquierda de A hay exactamente un punto
frontera pero, por las mismas razones, a la derecha de A sobre L,
hay exactamente otro punto frontera. Es decir, L corta a la frontera
de F en exactamente dos puntos. Entre estos
dos puntos todos los puntos son interiores y fuera de ellos, sobre L,
todos los puntos son exteriores. ![]()
Una propiedad de las figuras acotadas es la siguiente:
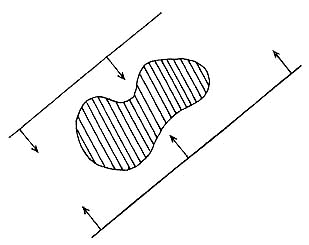
Una figura acotada tiene exactamente dos líneas soporte en cada dirección.
Demostración. Para ver esto, dibujemos primero dos líneas en la dirección dada, que tengan a la figura entre ambas. Luego deslicémoslas hasta que toquen a la figura (véase figura II.9).
Lo anterior no quiere decir que por cada punto de la frontera de una figura pasa una línea soporte. Esto, como ya lo habíamos mencionado antes, sólo sucede en las figuras convexas.
Por cada punto frontera de una figura convexa F pasa una línea soporte y viceversa.
Si por cada punto frontera de una figura F con puntos interiores, podemos trazar una línea soporte, es porque la figura F es una figura convexa.
Demostración. La demostración de la primera afirmación es fácil pero un poco tediosa. Como, además, no es relevante para el desarrollo subsecuente de este libro, la omitiremos. A continuación veremos la demostración de la segunda afirmación.
Para cercioramos de que F es una figura convexa necesitamos comprobar que el segmento que une cualquier par de puntos de F está también en F. Empezaremos verificando que entre un punto interior A y otro punto cualquiera B de F todos los puntos son parte de F. Si no fuera así, entre A y B habría un punto exterior y por lo tanto un punto frontera. Esto es imposible, como veremos a continuación. El punto C es un punto frontera de y alrededor de A hay una pequeña bolita totalmente contenida en F; así que trate de trazar una línea soporte de F por C, es decir, intente dibujar una línea que pase por C y deje tanto a la bolita alrededor de A como a B de un solo lado de la línea (ver figura II.10).
¡Imposible! ¿No es cierto? Imposible que exista un punto frontera entre A
y B. Pero si no hay puntos frontera, entonces tampoco hay puntos exteriores
entre A y B. Es decir, entre un punto interior y otro punto
cualquiera de F, todos los puntos
son puntos interiores de F.
Toca ahora comprobar que entre dos puntos frontera P y Q, todos
los puntos pertenecen a F. Llamemos L
a la línea que pasa por P y por Q. Como F
tiene puntos interiores existe un punto interior C que no está en la
línea L. Supongamos que está arriba de L. Entre C y P
todos los puntos son interiores, por lo tanto, entre cualquier punto del segmento
CP y el punto Q, todos los puntos son interiores. Es decir, todos
los puntos del interior del triángulo PCQ pertenecen a la figura F;
pero entonces todos los puntos del segmento PQ pertenecen a la figura
F de lo contrario, entre P y Q
habría un punto exterior, y por lo tanto una bolita alrededor de él, totalmente
fuera de F pero que se mete en el interior
del triángulo PCQ que está dentro de F
(ver figura II.11).![]()
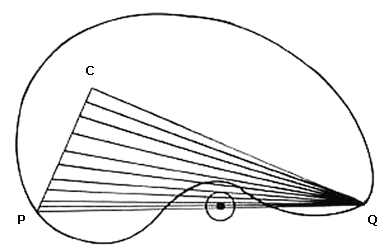
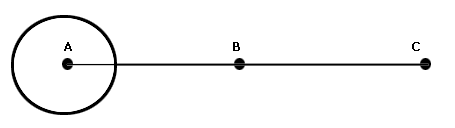
La figura convexa más pequeña que contiene a una figura f es llamada el casco convexo de f (ver figura II.12) Por supuesto, cuando la figura es convexa, su casco convexo y ella coinciden.
El casco convexo de f se obtiene al tomar la parte común de todas las posibles figuras convexas que contienen a f. En las figuras planas, otra forma de obtenerlo es considerar a Q más todos los posibles segmentos con extremos en f.
A continuación usaremos el hecho anterior para probar la siguiente propiedad de las figuras convexas.
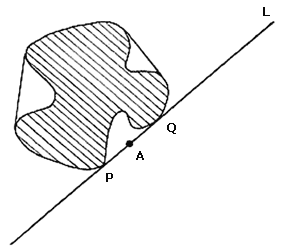
Si toda línea soporte de una figura f toca a la frontera de f en un solo punto, es porque la figura f es convexa.
Demostración. Vamos a ver que cualquier punto A de la frontera
del casco convexo de f está en f,
con lo cual f será convexa, pues coincide
con su casco convexo. Si A no estuviera en f,
entonces A estaría en algún segmento PQ con extremos P
y Q en Q —recordemos que el casco convexo de f
se obtiene mediante f más todos los posibles
segmentos con extremos en f. Por A
pasa una línea soporte L del casco convexo de f
(ver figura II.12). Como L debe pasar por A y dejar a P
y a Q de un mismo lado, forzosamente L debe de pasar tanto por
P como por Q, pero entonces L sería una línea soporte
de Q que lo toca en al menos dos puntos. ¡Imposible! A tiene que estar
en f.![]()
Volviendo a nuestra idea intuitiva de que las figuras convexas son las que no están abolladas, haremos notar otra de las propiedades características de las figuras convexas. Si una figura no está abollada, entonces cualquier punto que no esté en la figura puede ser separado de ella mediante una línea recta. No sucede así cuando la figura está abollada, precisamente en la abolladura se forma un hueco cuyos puntos no pueden separarse de la figura mediante una línea recta (ver figura II.13).
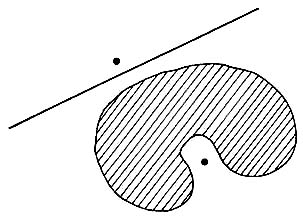
Más precisamente: Si una figura F es convexa y A es un punto que no está en ella, entonces existe una línea que separa al punto A de la figura F . Y viceversa, si en una figura F para cualquier punto A exterior a ella, siempre es posible trazar una línea recta que separe a la figura Q del punto A, es porque la figura F es convexa.
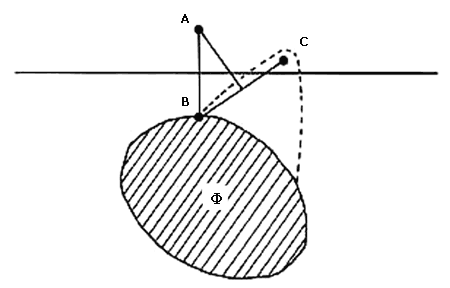
Demostración. Tomemos una figura convexa F y un punto cualquiera que no esté en ella. Llamémosle A. De entre todos los puntos de F, pongamos nuestra atención en aquel que se encuentre más cerca de A y llamémosle B (ver figura II.14). Mostraremos que la línea L, que pasa por el punto medio del segmento AB y es perpendicular a éste, separa a F del punto A. Es decir, mostraremos que "arriba de L" —del mismo lado de A— no hay ningún punto de F . Si existiera un punto C de la figura del mismo lado de A, entonces, por ser F convexa, el segmento BC estaría dentro de F y por lo tanto habría en este segmento un punto de F cuya distancia a A es más pequeña que la distancia de B a A. Esto es imposible pues habíamos escogido de antemano a B con la propiedad de ser el punto de F más cercano al punto A. Esto nos convence de que no existen puntos de F "arriba de L" y que, por lo tanto, la línea L separa a la figura F del punto A.
Supongamos ahora que tenemos una figura F con la propiedad de que, para cualquier punto A exterior a ella, hay una línea recta que separa a la figura F del punto A. Queremos ver que F es una figura convexa. Para tal efecto tenemos que tomar dos puntos P, Q de F y verificar que el segmento que los une está también en F. Yo afirmo que el segmento PQ está dentro de F. Si alguien —digamos usted, lector— quisiera negarlo tendría, por supuesto, que mostrarme un punto A entre P y F que no estuviera en F. Supongamos que pudiera mostrármelo, entonces yo le pediría que dibujara una línea que dejara a P y a Q de un lado y a A del otro —pues hemos acordado que F está separado de A por una línea. Como es obvio que esto no es posible, pues A está en el segmento P quedaría claro que fue un error suponer que A no estaba en F y concluiríamos —los dos— que todo el segmento PQ está dentro de F. Es decir, hemos demostrado que F es convexa verificando que el segmento que une cualquier par de puntos de F también esta en F.
Como consecuencia de este hecho tenemos que las figuras convexas tienen la siguiente propiedad.
La parte común de todos los semiplanos que contienen a una figura convexa F es precisamente la figura F.
Demostración. Por supuesto F está
en la parte común de todos los semiplanos que contienen a F,
sin embargo, esta última figura pudiese ser más grande. Todo punto exterior
a F puede separarse de F
mediante una línea; entonces, para cada punto exterior de F,
existe un semiplano que contiene a F pero
en el cual no está dicho punto. Por lo tanto, tampoco está en la parte común
a todos los semianos que contienen a F. Esto
prueba que la figura F no es más chica que
la parte común, sino que son iguales. ![]()
En este capítulo, hasta ahora hemos hablado de figuras, pero no de sólidos. Iniciaremos señalando que todo lo que se afirmó para figuras es cierto para sólidos si procedemos con las definiciones correctas.
Decimos que un sólido es convexo si cada vez que tomamos dos puntos en él, el segmento que los une pertenece también a él.
Un plano soporte de un sólido es un plano que toca al sólido pero que lo deja totalmente contenido de un lado (es decir, en uno de los semiespacios determinados por él).
En un sólido podemos distinguir también tres clases de puntos: los puntos interiores, los puntos exteriores y los puntos frontera. Sus definiciones son análogas a las dadas para figuras, excepto que ahora las "bolitas alrededor de los puntos" son realmente bolitas, es decir, son tridimensionales. Por supuesto, entre un punto interior de un sólido y otro que no esté en el sólido, siempre hay un punto frontera y, si el sólido es convexo, entre dos puntos del sólido o bien todos los puntos son interiores o todos son frontera.
Al igual que las figuras, los sólidos convexos pueden caracterizarse —es decir, todo sólido convexo tiene esta propiedad y, si algún sólido tiene esta propiedad, es porque el sólido es convexo— por medio de las siguientes propiedades:
| a) Por cada punto frontera del sólido pasa un plano soporte. |
| b) Cualquier punto exterior del sólido puede separarse de él mediante un plano. |
Finalmente, mencionaremos que si en un sólido, todos sus planos soporte lo tocan sólo en un punto, entonces el sólido es convexo.
Finalizamos este capítulo, una pequeña introducción a lo que se denomina convexidad geométrica. Desgraciadamente algunos aspectos bellísimos de ésta, como son la teoría de Helly o Radon, han quedado fuera del alcance de esta obra. La convexidad es y ha sido de crucial importancia para el desarrollo de las matemáticas, y ha acompañado a muchas de las ramas y resultados más importantes de la actualidad. Si le interesa profundizar en el tema, le recomiendo los bellísimos libros de V.G. Boltianskii citados en la bibliografía.