III. EL CÍRCULO
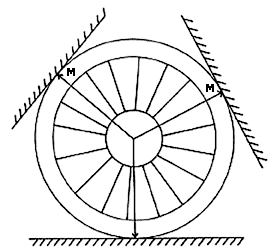
HAY ciertos hechos de la geometría que forman parte de la experiencia común; por ejemplo, todos sabemos que en una rueda, independientemente de su posición, el eje está exactamente arriba del punto donde la rueda toca al piso. Si en lugar de hacer rodar la rueda pensamos que el piso va tomando la posición de todas las tangentes del círculo, habremos demostrado un teorema de la geometría euclideana que dice que "si por un punto M de la frontera de un círculo trazamos una tangente, entonces ésta es perpendicular al radio del círculo que termina en M" (ver figura III.1).
Esta sencilla propiedad del círculo lo caracteriza, es decir, si existiese otra figura f y un punto K en su interior, con la propiedad de que, al rodar ésta, el punto K siempre está exactamente arriba del punto donde f toca al piso, entonces f necesariamente es un círculo y el punto K su centro.
A través de este libro tendremos con frecuencia la necesidad de convencernos de que determinada figura es un círculo puesto que posee la propiedad antes mencionada. Es por ello que este capítulo está dedicado íntegramente a convencemos del siguiente hecho:
Sea F una figura acotada y K uno de sus puntos interiores. Supongamos que por cada punto frontera M de F pasa una línea soporte que es perpendicular a la línea que pasa por K y por M; entonces F es un círculo con centro en K.
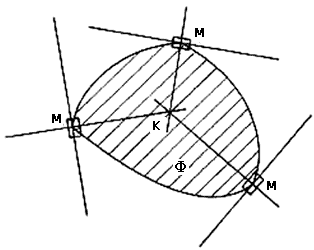
Demostración. Para empezar, F es convexa pues por cada punto de su frontera pasa una línea soporte. Además, cualquier línea que pase por el punto interior K, corta a la frontera de F en exactamente dos puntos y entre ellos (es decir, en el interior del segmento que los une) sólo hay puntos interiores.
La demostración de que F es necesariamente un círculo, si bien no es complicada, sí es un poco larga, motivo por el cual vamos a desglosarla, mostrando primero por separado cada una de las siguientes afirmaciones.
Supongamos que por cada punto frontera M de F pasa una línea soporte que es perpendicular a la línea que pasa por K y por M, entonces:
| i) Si C es un círculo que se encuentra dentro de F y toca a lo frontera de F enel punto A, entonces el centro de C, el punto K y el punto A están sobre una misma línea. |
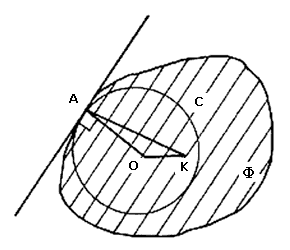
Figura III.3
| ii) Si L es una línea que pasa por K y corta a la frontera de F en los puntos P y Q, entonces el círculo cuyo diámetro es el segmento PQ está dentro de F. |
| iii) El centro del círculo de F es K. |
Por ejemplo, con respecto a i) algo como lo que se muestra en la figura III.3 no es posible.
Empezaremos con la afirmación i). Es decir: "Supongamos que C es un círculo dentro de F cuyo centro O es diferente de K. Si C toca a la frontera de F en un punto A, entonces A, K y O están en una misma línea."
Esto se debe, sencillamente, a que por A pasa una línea soporte de F perpendicular a la línea que pasa por K y por A (ver figura III.4) Esta línea soporte, por estar C dentro de F es una tangente de C que pasa por A. Como en un círculo los radios son perpendiculares a las tangentes, la línea que pasa por K y por A tiene que pasar también por O, el centro de C
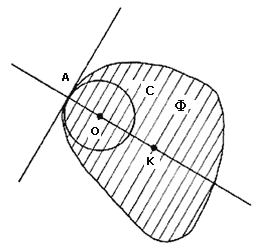
Veamos ahora la afirmación ii).
Tomemos una línea cualquiera que pase por K. Llamémosla L. Sabemos, pues F es convexa, que L corta a la frontera de F en exactamente dos puntos que llamaremos P y Q.
Nuestro siguiente propósito es convencernos de que: "el círculo cuyo diámetro es el segmento PQ, está dentro de F."
Es decir, queremos comprobar que el círculo con centro en el punto medio del segmento PQ, que pasa por P y por Q, está dentro de F . Para ver esto, pensemos en el punto medio del segmento PQ, al que llamaremos O.
Primero veremos el caso en el que K es diferente de O. Llamemos C al círculo más grande con centro en O que se encuentre dentro de F. Veremos que tanto P como Q están en C, con lo que habremos terminado con este caso. Como C es el círculo más grande con centro en O que se encuentra dentro de F, C tiene que tocar la frontera de F en algún punto, de lo contrario, sería posible hacer crecer a C un poquito más. Supongamos que C toca a la frontera de F en el punto A. Por i), el punto A se encuentra en la misma línea en la que se encuentran K y O, es decir, el punto A está en la línea L, pero en la línea L sólo hay dos puntos de la frontera de F que son P y Q (ver figura III.5). Es decir, A tiene que ser alguno de estos dos puntos. En la figura III.5 vemos que A es diferente de P y Q lo cual es imposible, pues en ese caso el punto A, el punto K y O no estarían alineados. Finalmente, como O es el punto medio del segmento PQ, el círculo C tiene que pasar tanto por P como por Q que es lo que queríamos.
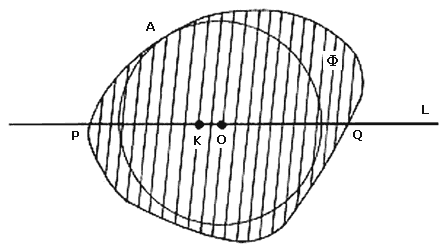
Nos falta ahora comprobar el caso en el que K es el punto medio del segmento PQ. Como antes, queremos ver que el círculo con centro K, que pasa por P y por Q, está dentro de F . Veremos primero que cualquier círculo que pase por P cuyo centro esté en el segmento PQ está dentro de F. Tomemos un punto cualquiera R entre P y K, y consideremos el círculo más grande con centro en R que esté dentro de F. Este círculo debe de tocar la frontera de F en algún punto, digamos en el punto B. Como B, K y R están en la misma línea, es decir, en la línea L, B tiene que ser o bien P o bien Q. Como R fue tomado entre P y K, B tiene que ser el punto P. Es decir, cualquier círculo que pase por P cuyo centro esté entre P y Q, está dentro de F, pero entonces todo el interior del círculo cuyo diámetro es el segmento PQ está dentro de F (ver figura III.6).
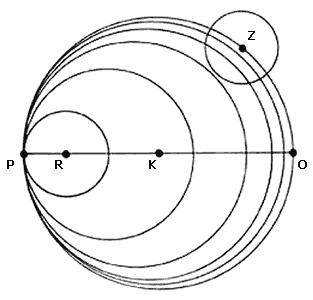
Todo lo anterior está muy bien, pero lo que queremos es ver que el círculo C, cuyo diámetro es PQ, está dentro de F . Si no fuera así, existiría un punto Z, distinto de P y de Q, en la frontera de C, que no estaría en F . Este punto Z sería un punto exterior de F, por lo que existiría una pequeña bolita alrededor de él, totalmente afuera de F; sin embargo, esto es imposible pues esta bolita mordería el interior del círculo C, que ya vimos que está dentro de Q (ver figura III.6). Hemos pues acabado de convencemos de que cualquier línea que pasa por K corta a F en un segmento y, el círculo cuyo diámetro es este segmento está dentro de F .
Continuemos con la afirmación iii), pero antes hablemos un poco sobre el circuncírculo y el incírculo de una figura cualquiera.
El círculo más pequeño que contiene a una figura y es llamado el circurncírculo de y. El círculo más grande contenido dentro de una figura y es llamado el incírculo de y ( ver Figura III.7).
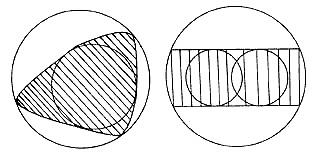
Éstos, por supuesto, no son necesariamente concéntricos. En un rectángulo existe un solo circumcírculo, pero varios incírculos (ver figura III.7). En general puede haber varios incírculos pero el circumcírculo es siempre único. Si existiera una figura y con dos circumcírculos, digamos C1 y C2, entonces y estaría dentro de C1 y dentro de C2 por lo que habría un círculo más pequeño que contiene a la parte común de C1 y C2 y por lo tanto a y (ver figura III.8).
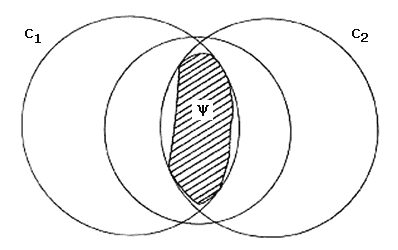
En seguida nos propondremos ver que para nuestra figura F, el incírculo es único pues su centro es el punto K.
Escojamos uno de los incírculos de F y llamémoslo u. Denotemos por O a su centro. El círculo u debe de tocar a la frontera de F en al menos dos puntos, de lo contrario, si sólo la toca en un punto, despegándolo sería posible encontrar un círculo más grande dentro de F. Sean X y Y dos puntos distintos que se encuentren en u, pero también en la frontera de F. Por i), en la línea que pasa por K y por X está O. Por la misma razón, en la línea que pasa por K y por Y está O, el centro de u. Las posibilidades que tenemos, ante estos dos hechos, son las siguientes:
a) K es igual a O, es decir, K es centro del incírculo u, o
b) K es distinto de O, en cuyo caso, el punto X y el punto Y son diametralmente opuestos en u, y K se encuentra en el segmento XY digamos entre X y O.
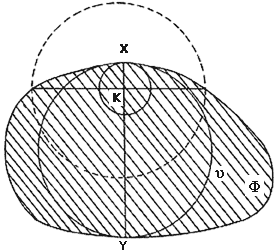
Para acabar de convencernos de que K es el centro de u y por lo tanto de que el incírculo de F es único, basta ver que el caso b) es imposible. Pensemos en una línea que pase por K y sea perpendicular al segmento XY (Véase figura III.9) Esta línea corta a F en un segmento, llamémoslo T. Esta misma línea corta a u en otro segmento, llamémoslo S. Por supuesto, S está dentro de T. El círculo con centro en K que pasa por X está dentro de u y sólo toca a la frontera de u en X. Por lo tanto, X esta en el interior del círculo cuyo diámetro es S, que está dentro del círculo cuyo diámetro es T que, a su vez, por ii), está dentro de F. Todo esto es imposible, porque X no es un punto interior sino un punto frontera de F. Por lo tanto, el caso b) no puede darse y la única posibilidad que nos queda es que K sea el centro de u.

Ahora, una vez que hemos acabado con las afirmaciones i), ii) e iii),
será muy fácil ver que el incírculo u de F,
y F coinciden. Sea P cualquier punto
de la frontera de F. ¿Cuál? El que usted escoja.
Comprobaremos que P está en el incírculo u.
Sea L la línea que pasa por K y por P. Como sabemos, L
corta a la frontera de F exactamente en P
y en algún otro punto, digamos Q. (Ver figura III.10). Por ii),
el círculo cuyo diámetro es el segmento PQ está dentro de F,
pero también contiene a u. Como u
es el círculo más grande dentro de F, u
y el círculo cuyo diámetro es el segmento PQ coinciden. Es decir, P
está en u. Finalmente, ya que P fue cualquier punto de la frontera de
F, el incírculo de F
y F coinciden, esto es: F
es un círculo.![]()