V. EQUILIBRIO EN CUALQUIER POSICIÓN
EL PROPÓSITO de este capítulo es dar una respuesta afirmativa al siguiente problema de Ulam.
| Si un sólido descansa en equilibrio en cualquier posición en la que se le deje sobre una superficie plana horizontal, ¿deberá ser éste una esfera? |
Empezaremos pensando en la versión bidimensional del problema. Para abordarlo necesitamos algunas definiciones, —no muchas— y un criterio de equilibrio.
Para todo sólido, o para toda figura, existe un punto que se comporta como si toda la masa estuviese concentrada en él. A este punto lo llamaremos el centro de masas de la figura o del sólido.
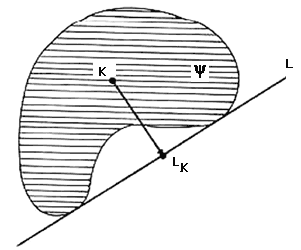
Si y es una figura, K es su centro de masas y L es una línea soporte de y, denotamos por LK al punto sobre L que es el pie de la perpendicular a L que pasa por K (ver figura V.1). Si pensamos que L es el piso, entonces LK denota al punto sobre el piso que está exactamente abajo del centro de masas de y.
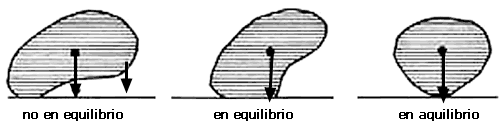
Decimos que una figura y está en equilibrio con respecto a una línea soporte L de y si sobre L, tanto a la izquierda de LK (incluyendo a LK como a la derecha de LK (incluyendo a LK podemos encontrar puntos de y. Intuitivamente estos puntos de y, a la izquierda y a la derecha de LK, serán los puntos de apoyo de la figura y que permiten que ésta no se voltee ni hacia la derecha ni hacia la izquierda. El caso extremo en el que LK es el único punto en el que se apoya y, la figura está en equilibrio, pues hemos acordado que LK está tanto a la derecha como a la izquierda de sí mismo. La siguiente serie de figuras ilustra, de acuerdo con el criterio anterior, cuando una figura está o no en equilibrio.
Una figura está en equilibrio en cualquier posición en la que se le deje si está en equilibrio con respecto a cualquiera de sus líneas soporte.
A continuación demostraremos que si una figura "está en equilibrio en cualquier posición en la que se le deje", es porque la figura es un círculo. Recordemos que una interpretación física de este problema se refiere a que el cilindro circular es el único cilindro que tiene la propiedad de que, mientras su eje es paralelo a la superficie plana, permanece en equilibrio sin voltearse, en cualquier posición en la que se le deje.
Si una figura y está en equilibrio en cualquier posición en la que se le deje y L es una línea soporte de y entonces L toca a la figura y sólo en el puntoLK.
Demostración. Supongamos que no: supongamos que existe una linea soporte L —podemos pensarla como el piso— y un punto X sobre ella, distinto de LK en donde y se apoya (ver figura V.3). Veremos que esto es imposible, pues si así fuera existiría una (posición) línea soporte con respecto a la cual y no está en equilibrio. De hecho, intuitivamente, la demostración consistirá de "palanquearse" en el punto X para desequilibrarla.
Sea R el rayo que parte de K y pasa por el punto medio de LK y X, al que llamaremos a. Perpendicular a este rayo, quizá muy abajo, existe una línea L1 que no toca a la figura y y que corta al rayo R en un punto al que llamaremos b. Vamos a deslizar paralelamente la línea L1 hasta que toque a la figura y. Al deslizarla, el punto b se irá desplazando sobre R hacia el punto K. Sean L1' y b' las posiciones finales de L1 y b en su viaje hacia y. En su camino, b nunca sale a la superficie. Quiero decir; "el punto b' está bajo tierra y con él también uno de los rayos de L1' que empieza en b' " (véase figura V.3). Si no fuera así, querría decir que en su camino b pasó por a. Un poquito antes de ese momento la línea L1 aún no tocaba a la figura —quedamos en que la línea L1 se paraba en el momento en que tocara a la figura—, pero esto es imposible pues, siendo a el punto medio de X y LK' , la línea que pasa por a y es paralela a L1 deja a K de un lado y a X del otro.
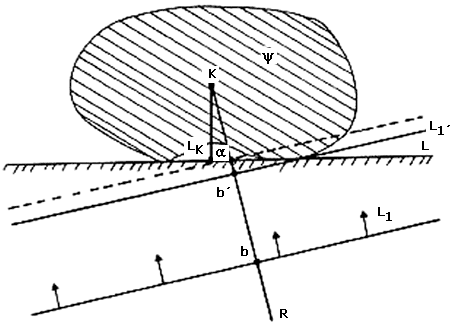
Giremos tantito la cabeza y pensemos que ahora el piso es L1.
Es claro que y no está en equilibrio con respecto
a L1 pues a un lado de b' no hay
ningún punto en donde y se apoye. ![]()
Si una figura y está en equilibrio en cualquier posición en la que se le deje es porque la figura es un círculo.
Demostración. Para mostrar que la figura y
es un círculo vamos a hacer uso del resultado principal del capítulo III.
Con tal motivo necesitamos comprobar que por cada punto frontera M de
y pasa una línea soporte que es perpendicular
al segmento KM, donde K es el centro de masas de y.
Como cualquier línea soporte de y corta a
y en un solo punto, la figura y
es convexa. Tomemos un punto M de la frontera de y
y ya que y es convexa tracemos una línea soporte
L de y por M. Nosotros sabemos que L corta a la figura
y precisamente en el punto LK,
donde LK es el punto sobre L
con la propiedad de que el segmento MLK
es perpendicular a L. Por tanto, el segmento KM es perpendicular
a la línea soporte L, que era lo que necesitábamos comprobar. Una vez
hecho esto, por el resultado principal del capítulo III, sabemos que
y es un círculo.![]()
Pasemos a trabajar con sólidos que estén en equilibrio en cualquier posición en la que se les deje.
En forma análoga a lo hecho en las figuras, si q es un sólido, K es su centro de masas y P es una plano soporte de q, denotamos por PK al punto sobre P que es el pie de la perpendicular a P que pasa por K (ver figura V.4). Si pensamos que P es el piso, entonces PK denota al punto sobre el piso que está exactamente abajo del centro de masas de q.
Intuitivamente, un sólido q está en una posición en la que pierde el equilibrio, es decir, se cae, si sobre el piso existe una línea que separa a todos los puntos de apoyo del sólido, del punto del piso que está abajo del centro de masas (ver figura V.4).
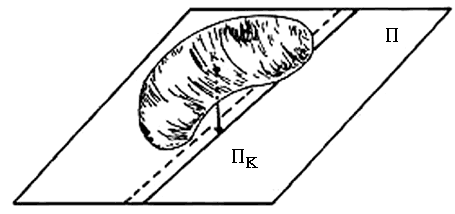
Fíjese que en tal caso existe una línea en el piso que pasa por el punto que está abajo del centro de masas, que no toca al sólido y que deja a los puntos, en los que el sólido se apoya sobre el piso, en uno de los lados determinados por ella
Es por esto que vamos a decir que un sólido q está en equilibrio con respecto a un plano P si cualquier línea de P que pase por Pk, o bien toca a q o deja a puntos de Q a ambos lados de ella.
De hecho, lo que estamos diciendo es que q está en equilibrio con respecto al plano P, si cualquier subconjunto convexo de P que contenga a los puntos en los que q toca a P, también contiene a Pk. Es decir, si Pk está en el casco convexo de la parte común entre P y q.
Finalmente, un sólido q está en equilibrio en cualquier posición en la que se le de, si está en equilibrio con respecto a cualquiera de sus planos soporte.
Supongamos que q es un sólido que está en equilibrio en cualquier posición en la que se le deje; entonces todas sus sombras son figuras que están en equilibrio en cualquier posición en las que se les deje. ¿Ha visto usted perder el equilibrio a alguna sombra sin que lo pierda quien la proyecta?
Demostración. Vamos a ver que si en alguna dirección la sombra de q no está en equilibrio en cualquier posición en la que se le deje; entonces, el sólido tampoco está en equilibrio en cualquier posición en la que se lo deje. De esta manera, si q está en equilibrio también lo estarán todas sus sombras. Supongamos por tanto que la proyección de q en la dirección d sobre el plano P1, a la que llamaremos y no está en equilibrio en cualquier posición en la que se le deje (ver figura V.5). Entonces existe en P1 una línea soporte L de y y un punto T de ella que no está en y, pero que tiene la propiedad de que todos los puntos en los que y toca a L están de un lado de T y Lk está del otro lado. Llamemos P a el plano paralelo a la dirección d que corta a P1 en L, y sea L1 la línea paralela a la dirección d que corta a P1 en el punto T. Es fácil ver que P es un plano soporte de q y que la línea L1 de P no toca a q pero deja a los puntos en los que q se apoya en P de un lado y a PK del otro lado. Evidentemente, el sólido Q no está en equilibrio con respecto al plano soporte P.
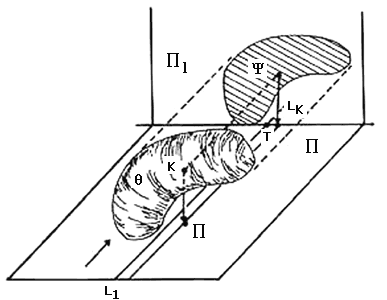
De lo anterior se deduce que si un sólido está en equilibrio en cualquier posición en la que se le deje entonces todas sus proyecciones son círculos y, por lo tanto, que:
Si un sólido descansa en equilibrio en cualquier posición en la que se le
deje sobre una superficie plana horizontal, entonces el sólido es una esfera.