VII. RELATIVIDAD Y GRAVITACI�N
Los a�os de b�squeda en la oscuridad de una verdad
que uno siente pero no puede expresar, el deseo intenso y la alternancia
de confianza y desaz�n, hasta que uno encuentra el camino a la claridad
y comprensi�n, s�lo son familiares a aqu�l que los ha experimentado.
|
Los or�genes de la teor�a general de la relatividad,
A.EINSTEIN |
SEG�N el principio b�sico de la teor�a de la relatividad, los
fen�menos f�sicos obedecen leyes que no dependen del sistema de referencia desde
el cual se observan. Pero este postulado, tal como hemos visto hasta ahora,
se aplica s�lo a sistemas inerciales, aquellos que se mueven en l�nea recta
y a velocidad constante. Por el contrario, en un sistema no inercial (como un
veh�culo que forma una curva o se enfrena) act�an fuerzas que permiten discernir
el movimiento. Y sobre la superficie de la Tierra se puede distinguir entre
arriba y abajo observando simplemente la ca�da de un cuerpo. En realidad, un
sistema de referencia inercial perfecto debe estar aislado en el espacio sideral,
lejos de cualquier cuerpo que lo atraiga gravitacionalmente.
Para superar estas limitaciones, Einstein investig� durante varios a�os la posibilidad de modificar la teor�a de la gravitaci�n de Newton para hacerla compatible con el principio de relatividad. La clave para �l fue la existencia de una profunda relaci�n entre fuerzas inerciales y fuerzas gravitacionales, Citemos sus propias palabras:
Estaba yo sentado en mi sill�n de la oficina
de patentes de Berna cuando, de repente, tuve una ocurrencia: "Si
una persona cae libremente, no siente su propio peso." Qued� at�nito.
Esta idea tan simple me impresion� profundamente. Me impuls� hacia
una teor�a de la gravitaci�n. |
La teor�a de la gravitaci�n de Einstein empez� a tomar forma en 1907, cuando a�n trabajaba en Berna, hasta culminar en su versi�n definitiva en 1916: la teor�a general de la relatividad. La versi�n primera de la relatividad, aqu�lla que hemos discutido hasta ahora y que se restringe a sistemas de referencia inerciales, se conoce como la teor�a restringida de la relatividad o tambi�n, teor�a especial de la relatividad.
La piedra angular de la relatividad general es un principio f�sico que nos remonta una vez m�s al mism�simo Galileo.
En la f�sica aristot�lica, se cre�a que los cuerpos pesados ca�an m�s r�pidamente que los cuerpos ligeros. Cuenta una famosa leyenda (que bien puede ser ver�dica) que Galileo Galilei demostr� lo contrario al soltar simult�neamente desde lo alto de la Torre de Pisa dos piedras de peso desigual; ante la mirada del p�blico incr�dulo, las dos piedras llegaron al suelo exactamente al mismo tiempo (Figura 23). As�, Galileo comprob� que la trayectoria de un cuerpo bajo el influjo gravitacional de la Tierra es independiente de la masa del cuerpo. (En todo caso el movimiento puede depender de la forma del cuerpo, pero �nicamente por la resistencia que le opone el aire. Es cierto que una pluma cae m�s lentamente que una bola de plomo, pero esto se debe exclusivamente a que el aire retarda la ca�da de la pluma. En una campana al vac�o o en la Luna, donde no hay atm�sfera; la pluma y la bola de plomo caen exactamente con la misma velocidad.)
En t�rminos m�s precisos, lo que Galileo demostr� fue la equivalencia entre la masa inercial y la masa gravitacional. Expliquemos a continuaci�n estos dos conceptos, que muchas veces se confunden.
Figura 23. El experimento de Galileo.
La masa es una medida de la cantidad de materia (y energ�a, de acuerdo con la relatividad) que contiene un cuerpo. La Tierra atrae gravitacionalmente a los cuerpos masivos con una fuerza proporcional a su masa (como descubri� Newton), as� que la manera m�s com�n de determinar la masa de un cuerpo consiste en medir esa fuerza gravitacional; de aqu� el concepto del peso, que es en realidad una medida de la fuerza gravitacional ejercida por la Tierra sobre el objeto pesado. Pero no hay que olvidar que la atracci�n gravitacional depende tambi�n de la masa del cuerpo atractor y disminuye con la distancia: por convenci�n, la masa y el peso de un cuerpo se toman como iguales a nivel del mar. Una bolsa de frijoles que pesa un kilogramo a nivel del mar ser� un gramo m�s liviana a 3 000 metros de altura, pesar�a s�lo 165 gramos sobre la superficie de la Luna, y no pesa nada en el espacio extraterrestre lejos de cuerpos que la atraigan.
Pero existe una segunda manera de determinar la masa de un cuerpo, y es por medio de la segunda ley de Newton, seg�n la cual un cuerpo adquiere una aceleraci�n directamente proporcional a la fuerza que se le aplica e inversamente proporcional a su masa. Si empujamos con la misma fuerza un carro que pesa 10 kilogramos y otro que pesa 100 kilogramos, el primero se acelerar� 10 veces m�s que e1 segundo, de donde podemos deducir que el primer carro es 10 veces menos masivo, que el segundo.
As�, existen dos maneras de determinar la masa de un cuerpo. Una es con la que se mide la masa gravitacional. Otra forma es utilizar la segunda ley de Newton: midiendo la inercia que un cuerpo opone a la fuerza que se le aplique, con lo que se determina la masa inercial. Ahora bien, un principio b�sico, al que nos hemos acostumbrado tanto que nos parece evidente, es que la masa inercial y la masa gravitacional de cualquier cuerpo son iguales. Este es el principio de equivalencia que Galileo formul� por primera vez y que Einstein utiliz� como fundamento de su teor�a de la relatividad general.
�Qu� tiene de sorprendente que la masa inercial y la masa gravitacional sean iguales? Para aclarar este punto recordemos que la fuerza gravitacional es s�lo una de las fuerzas de la Naturaleza. La fuerza electromagn�tica es muy distinta de la gravitacional y es la responsable de que los cuerpos cargados el�ctricamente se atraigan o se rechacen, o que los electrones de los �tomos permanezcan unidos a los n�cleos at�micos. Existen tambi�n otras fuerzas que act�an s�lo a distancias subat�micas: la nuclear, que mantiene unidos los protones y neutrones en un n�cleo, y d�bil, que produce el decaimiento beta.
Imaginemos ahora un planeta que posee una carga el�ctrica y que, por lo tanto, atrae a los cuerpos en su superficie con una fuerza el�ctrica, y no gravitacional. Un Galileo de ese planeta podr�a repetir el experimento de lanzar dos piedras con cargas el�ctricas distintas y preguntarse �caer�n al mismo tiempo? La respuesta es negativa, porque adem�s de la carga influye la masa inercial en el movimiento de un cuerpo. Si dos piedras tienen la misma carga el�ctrica; pero la masa inercial de una es de un gramo y la de otra es de una tonelada, la que se mover� m�s r�pidamente al ser atra�da por otra carga ser� evidentemente la m�s ligera.
El origen de la confusi�n entre masa inercial y gravitaci�n es que nos hemos acostumbrado a llamar masa gravitacional a lo que en realidad es la carga gravitacional. Una diferencia fundamental entre la fuerza gravitacional y la electromagn�tica es que se puede cargar o descargar el�ctricamente un cuerpo, pero la carga gravitacional de un cuerpo est� fijada por su masa inercial y no se puede "descargar gravitacionalmente" (excepto en las pel�culas de ciencia ficci�n donde vemos cuerpos masivos desafiando a la gravedad junto a otros que caen normalmente).
La implicaci�n m�s inmediata del principio de equivalencia es que todos los cuerpos caen de la misma forma, independientemente de la masa que posean. El mismo Isaac Newton confirm� experimentalmente este principio antes de publicar las leyes de la mec�nica que hab�a descubierto. El experimento de Newton —m�s preciso que el realizado por Galileo en Pisa— consisti� en medir el periodo de oscilaci�n de varios p�ndulos de distintos pesos y materiales: despu�s de un largo tiempo, los p�ndulos, cuyo movimiento se hab�a sincronizado inercialmente, segu�an oscilando con el mismo periodo. Y tres siglos despu�s de los experimentos de Galileo y Newton, el principio de equivalencia se confirm� con t�cnicas modernas, con un margen de error de apenas una parte en un mill�n de millones.
La equivalencia entre masa (o carga) gravitacional y masa inercial es un principio b�sico de la naturaleza, cuyo origen a�n estamos lejos de comprender. A finales del siglo XIX, el f�sico alem�n Ernst Mach propuso que la masa inercial de un cuerpo est� enteramente determinada por la atracci�n gravitacional de todos los dem�s cuerpos en el Universo, de donde la relaci�n entre inercia y gravitaci�n. Una conjetura muy interesante que no se ha podido todav�a demostrar (o refutar), pero que inspir� a Einstein para fundamentar su teor�a de la relatividad general.
Existe una relaci�n muy profunda entre sistemas de referencia no inerciales y sistemas de referencia sometidos a fuerzas gravitacionales, relaci�n que se puede entender con un ejemplo dado por el mismo Einstein.
Supongamos que nos encontramos encerrados en una caja colocada sobre la superficie terrestre. En su interior, sentimos la fuerza gravitacional de la Tierra que nos atrae al suelo, al igual que todos los cuerpos que se encuentran a nuestro alrededor. Al soltar una piedra, �sta cae al suelo aumentando continuamente su velocidad, es decir aceler�ndose a raz�n de 9.81 metros por segundo cada segundo, lo que equivale, por definici�n, a una aceleraci�n de 1 g. Por supuesto, en el interior de la caja la fuerza que act�a sobre un cuerpo es proporcional a su masa gravitacional (Figura 24).
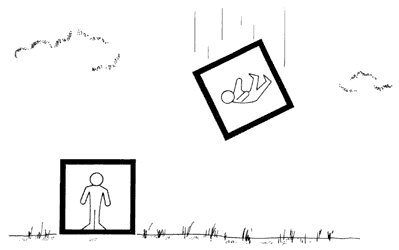
Figura 24. El pasajero en un veh�culo que cae libremente no siente ninguna fuerza gravitacional.
Ahora, consideramos el caso de una caja situada en el espacio, lejos de la influencia gravitacional de cualquier planeta o estrella. Si esa caja est� en reposo, todo lo que se encuentra en su interior flota ingr�vidamente. Pero si la caja se acelera, aumentado su velocidad a raz�n de 9.81. metros por segundo cada segundo (1 g), los objetos en su interior se quedan rezagados y se pegan al suelo; m�s a�n, un cuerpo que se suelte dentro de ella se dirigir� al suelo con una aceleraci�n de l g. Evidentemente, la caja acelerada es un sistema de referencia no inercial, y las fuerzas, que aparecen en su interior son fuerzas inerciales que dependen de la masa inercial de los cuerpos sobre los que act�an (Figura 25).
Y ahora la pregunta fundamental: �pueden los ocupantes de una caja determinar por medio de experimentos f�sicos si se encuentran en reposo sobre la superficie de la Tierra o se encuentran en el espacio, en movimiento acelerado? La respuesta es no, porque el principio de equivalencia no permite distinguir, dentro de la caja, entre una fuerza gravitacional y una inercial.
Podemos imaginarnos otra posible situaci�n. Esta vez la caja es un elevador que se encuentra en un edificio terrestre, pero su cable se rompe y cae libremente. Sus ocupantes caen junto con la caja (Figura 24) y, mientras dura la ca�da, no sienten, ninguna fuerza gravitacional, exactamente como si estuvieran en el espacio extraterrestre.
Otra situaci�n, que se ha vuelto familiar en los �ltimos a�os, es la de los cosmonautas que vemos flotar ingr�vidos dentro de sus veh�culos colocados en �rbita alrededor de la Tierra. Si no perciben ninguna fuerza gravitacional no es porque est�n tan alejados de la Tierra que no resientan su atracci�n, es porque �l veh�culo espacial y sus tripulantes se encuentran en ca�da libre. Esto puede no coincidir con la idea, com�n de Luna ca�da; pero hay que recordar que, estrictamente hablando, un cuerpo se encuentra en ca�da libre si se mueve �nicamente bajo el influjo de una fuerza gravitacional sin otro tipo de restricci�n. Un sat�lite terrestre efectivamente est� en ca�da libre, pero nunca choca con la Tierra por la curvatura de �sta, como se puede ver en la figura 26. En resumen, un veh�culo espacial en �rbita, con sus motores apagados y sin fricci�n del aire por encontrarse fuera de la atm�sfera, es un ejemplo perfecto de un sistema inercial: sus ocupantes no pueden decidir, sin mirar por las escotillas, si est�n en �rbita alrededor de la Tierra o en reposo lejos de todo cuerpo celeste.
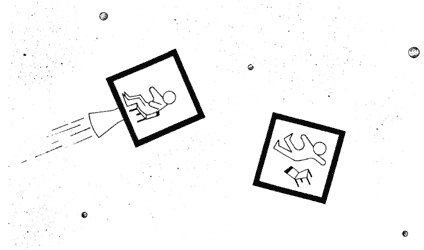
Figura 25. El pasajero en un veh�culo acelerado puede pensar que un planeta lo atrae gravitacionalmente.
As�, un sistema de referencia inercial es equivalente a un sistema de referencia en ca�da libre, y del mismo modo un sistema no inercial es equivalente a un sistema de referencia sometido a la fuerza gravitacional. En consecuencia, se puede extender el principio de relatividad a sistemas no inerciales si se toma en cuenta a la gravitaci�n. Pero Einstein fue m�s all� de esta simple comprobaci�n.
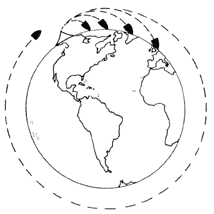
Figura 26. Un sat�lite en �rbita es un caso extremo de proyectil de ca�da libre.
Regresemos al ejemplo de la caja en ca�da libre, pero esta vez supongamos que la caja es lo suficientemente grande para hacer el siguiente experimento: col�quense dos canicas en cada extremo del compartimento, como se indica en la figura 27. Como las canicas se hallan tambi�n en ca�da libre, permanecen fijas, flotando, para los ocupantes de la caja. Sin embargo, las trayectorias de ambas no son exactamente rectas paralelas, sino rectas que convergen al centro de la Tierra. En consecuencia, vistas desde la caja, las dos canicas no est�n estrictamente fijas, sino que parecen acercarse lentamente una a otra. Este efecto casi imperceptible no ocurrir�a si la caja estuviera en el espacio extraterrestre, lejos de todo influjo gravitacional, ya que las dos canicas permanecer�an exactamente donde se colocan.
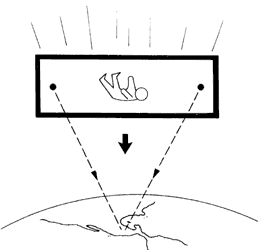
Figura 27. Manifestaci�n de la fuerza gravitacional en una caja en ca�da libre suficientemente grande.
El experimento anterior implica que la equivalencia entre sistema inercial y sistema en ca�da libre debe formularse con m�s precisi�n: Los dos sistemas son equivalentes en una regi�n peque�a del espacio, pero pueden distinguirse uno del otro si se realizan experimentos f�sicos sobre distancias suficientemente grandes.
Esta comprobaci�n condujo a Einstein a relacionar la gravitaci�n con las propiedades geom�tricas de una superficie. Por ejemplo, sabemos que la Tierra es redonda, pero su curvatura no se manifiesta en una regi�n peque�a. A escala humana, nuestro planeta parece plano y es s�lo sobre distancias de varios cientos de kil�metros que los efectos de la curvatura se vuelven apreciables. Si se trazan dos rectas paralelas sobre la superficie terrestre, estas rectas permanecen paralelas inicialmente manteni�ndose constante la distancia entre ellas; pero si las rectas se prolongan cientos de kil�metros empezar�n a converger debido a la curvatura de la Tierra, y acabaran por unirse en alg�n punto (Figura 28). Las rectas trazadas sobre la superficie de la Tierra son m�s bien segmentos de c�rculo; es s�lo a escalas peque�as que parecen rectas. El concepto de recta pierde su sentido sobre una superficie curva y es m�s preciso referirse a curvas de longitud m�nima: sobre una superficie plana, la recta es la curva de m�nima longitud entre dos puntos dados, pero sobre la superficie de una esfera la curva m�s corta entre dos puntos es un segmento de c�rculo (Figura 29).
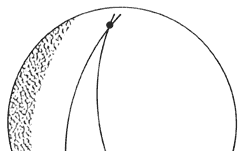
Figura 28. Dos "paralelas" terminan uni�ndose sobre una superficie curva.
Ahora bien, las dos "paralelas" trazadas sobre la superficie de la Tierra, y que terminan por unirse debido a la curvatura de �sta, recuerdan las trayectorias de las dos canicas en el elevador que cae. En el primer caso, se tiene un efecto debido a la curvatura de una superficie, mientras que en el segundo caso se manifiesta una fuerza gravitacional. El primer efecto es geom�trico y el segundo gravitacional. Una superficie curva parece plana en una regi�n suficientemente peque�a, y del mismo modo una fuerza gravitacional no es detectable en un veh�culo de dimensiones reducidas y en ca�da libre.
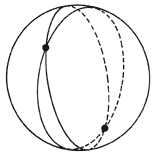
Figura 29. Las geod�sicas son las curvas de menor longitud sobre una superficie curva.
Todas estas analog�as condujeron a Einstein a la conclusi�n de que la fuerza gravitacional puede interpretarse como un efecto geom�trico. S�lo que, a diferencia de la superficie terrestre, en la teor�a de Einstein el espaciotiempo es curvo y la gravitaci�n es la manifestaci�n de su curvatura.
LA CURVATURA DEL ESPACIOTIEMPO
Consideremos primero el caso m�s simple de un espacio curvo de dos dimensiones.
Un ejemplo es la superficie de una esfera, que es de dos dimensiones
porque se necesitan dos n�meros, las coordenadas de longitud y latitud, para
localizar un punto sobre ella. Las curvas de menor longitud entre dos, puntos
son el equivalente de las rectas y se llaman en lenguaje matem�tico, geod�sicas.
A diferencia de las rectas sobre una superficie plana, dos geod�sicas inicialmente
paralelas se cruzan en alg�n punto (Figura 29); en general, los postulados y
teoremas de la geometr�a elemental —que se aprende en la escuela— no
son v�lidos sobre superficies curvas donde las geod�sicas sustituyen a las rectas.
A mediados del siglo XIX, el matem�tico alem�n Georg Friedrich Bernhard Riemann (1826-1866) tuvo la idea de extender el concepto de superficie curva a un espacio con cualquier n�mero de dimensiones. En un espacio as�, cada "punto" est� determinado por medio de n coordenadas; m�s a�n, se puede postular una f�rmula para medir la "distancia" entre dos puntos, lo cual permite construir geod�sicas, que sustituyen a las rectas en el espacio ordinario. Es evidente que, en un espacio curvo, los postulados y teoremas b�sicos de la geometr�a cl�sica no se cumplen; las geod�sicas pueden cruzarse en m�s de un punto, las paralelas no mantienen constante la distancia entre ellas, la suma de los �ngulos de un tri�ngulo no da 180°, etc�tera.
Riemann demostr� que las propiedades b�sicas de un espacio curvo est�n determinadas exclusivamente por la f�rmula para medir "distancias". Escoger una manera de medir esta distancia equivale a definir un espacio riemanniano, que es un espacio curvo de dos, tres, cuatro o cualquier n�mero de dimensiones.
A diferencia de las superficies, que son espacios de dos dimensiones, los espacios curvos de tres o m�s dimensiones no se pueden visualizar. Sin embargo, es posible definirlos y manejarlos matem�ticamente sin ninguna dificultad de principio; los espacios riemannianos son un excelente ejemplo de un concepto que s�lo se puede describir en lenguaje matem�tico.
Como una visi�n prof�tica, Riemann especul� que podr�a existir una relaci�n entre las propiedades geom�tricas del espacio y los procesos f�sicos que ocurren en �l. Sin embargo, sus trabajos fueron considerados durante mucho tiempo como simples curiosidades matem�ticas, ajenas al mundo real. No fue sino hasta la segunda d�cada del siglo XX cuando Einstein lleg� a la conclusi�n de que el espacio tiempo en el que vivimos es un espacio riemanniano de cuatro dimensiones.
Einstein public� la versi�n definitiva de su teor�a de la relatividad general en el n�mero de noviembre de 1915 del Bolet�n de la Academia de Ciencias de Berl�n, en plena primera Guerra Mundial. Para la formulaci�n de esta teor�a cont� con la ayuda de su amigo el matem�tico Marcel Grossman, quien le hab�a despertado el inter�s en los trabajos de Riemann. La esencia de la teor�a de Einstein es que la masa de un cuerpo deforma el espaciotiempo a su alrededor. En ausencia de masa, el espaciotiempo es plano y una part�cula se mueve en l�nea recta porque nada influye sobre su trayectoria, pero en presencia de una masa gravitante, el espaciotiempo se curva y una part�cula se mueve a lo largo de una geod�sica. De acuerdo, con esta interpretaci�n de la gravedad, un planeta gira alrededor del Sol porque sigue una trayectoria geod�sica en el espaciotiempo deformado por la masa solar.
En la teor�a de la gravitaci�n de Newton, se puede calcular la atracci�n gravitacional ejercida por una distribuci�n dada de masa por medio de una ecuaci�n matem�tica. En la teor�a de Einstein, se calcula la curvatura del espaciotiempo, pero la situaci�n es bastante m�s complicada porque no s�lo la masa sino tambi�n la energ�a ejerce una acci�n gravitacional. En su art�culo de 1916, Einstein dedujo la ecuaci�n matem�tica que relaciona la geometr�a del espaciotiempo con la distribuci�n de masa y energ�a: esta f�rmula se conoce como ecuaci�n de Einstein y es la base de la relatividad general (Figura 30).
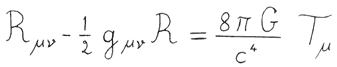
Figura 30. La ecuaci�n de Einstein de la relatividad general.
Si los f�sicos no se hab�an percatado antes de Einstein de que el espacio es curvo es porque la gravedad de la Tierra y del Sol induce una curvatura extremadamente leve. La situaci�n es semejante a la de los hombres antiguos que cre�an que la Tierra era plana, ya que su curvatura es imperceptible a peque�a escala. Como veremos a continuaci�n, la curvatura del espaciotiempo se manifiesta plenamente a la escala del Universo mismo, o cerca de cuerpos celestes cuya atracci�n gravitacional es extremadamente intensa. En nuestro Sistema Solar, debemos conformarnos con efectos casi imperceptibles para confirmar la relatividad general.
Figura 31. Einstein en Estados Unidos.
