VI. RELATIVIDAD Y Y MEC�NICA CU�NTICA

LA F�SICA del siglo XX se sustenta sobre dos pilares: la teor�a de la relatividad y la mec�nica cu�ntica. La primera obra casi exclusiva de Albert Einstein, describe los fen�menos naturales en los que est�n involucradas velocidades cercanas a la de la luz. La segunda, en cuya formulaci�n particip� una pl�yade de grandes f�sicos de principios de siglo,¹ es la mec�nica del mundo de los �tomos y las part�culas que los constituyen.

As� como la teor�a de la relatividad introdujo conceptos que chocaron con el sentido com�n, la mec�nica cu�ntica expuso una descripci�n del mundo microsc�pico que en nada se parec�a al de la experiencia diaria. De acuerdo con la mec�nica cu�ntica, las part�culas at�micas no se comportan como los objetos del mundo macrosc�pico, sino que tienen propiedades a la vez de part�culas y de ondas.

El lector recordar� que ya tuvimos ocasi�n de conocer una part�cula con esta caracter�stica: el fot�n, que a veces se manifiesta como onda y a veces como part�cula. Esta es una propiedad de todas las part�culas elementales —electrones, protones, neutrones, etc.— que constituyen los �tomos, por lo que los fen�menos en ese nivel se producen de acuerdo a leyes muy peculiares. Por principio de cuentas, es imposible caracterizar una part�cula elemental por su posici�n y su velocidad, tal como ocurre en la f�sica newtoniana. Al contrario, en la mec�nica cu�ntica s�lo se puede calcular la probabilidad de encontrar una part�cula en cierto estado f�sico. Tal probabilidad se obtiene a partir de una expresi�n matem�tica, la funci�n de onda.

En la mec�nica newtoniana se calcula la posici�n y la velocidad de una part�cula a partir de ecuaciones matem�ticas, que relacionan el movimiento de la part�cula con la fuerza que se le aplica de acuerdo con la segunda ley de Newton (fuerza = masa X aceleraci�n). En cambio, en la mec�nica cu�ntica se calcula la probabilidad de encontrar una part�cula en cierto estado f�sico, utilizando ecuaciones matem�ticas, en particular la ecuaci�n deducida por el f�sico alem�n Erwin Schr�dinger en 1926, que relaciona la funci�n de onda de la part�cula con la fuerza aplicada sobre ella.

Gracias a esta ecuaci�n, los f�sicos lograron resolver un gran n�mero de problemas relacionados con los �tomos y las part�culas que los componen. Un nuevo nivel de la realidad se hab�a revelado, donde reg�an leyes totalmente distintas las de nuestro mundo macrosc�pico.

La ecuaci�n de Schr�dinger tiene un rango de validez muy amplio, pero restringido a fen�menos en los que no se involucran velocidades cercanas a la de la luz. La mec�nica cu�ntica naci� como una extensi�n de la mec�nica newtoniana al mundo at�mico y, por ello precisamente llevaba inherentes las limitaciones b�sicas de �sta. En los a�os treinta, los fen�menos relativistas a�n no ten�an cabida en la nueva f�sica cu�ntica. Era necesario, pues, unir la mec�nica cu�ntica y la relatividad.

P. A. M. DIRAC Y EL ANTIMUNDO

La ecuaci�n de Schr�dinger es compatible con el principio de relatividad de Galileo, pues est� basada en los principios de la mec�nica newtoniana. Generalizar esa ecuaci�n para hacerla compatible con la relatividad de Einstein no parec�a, en principio, demasiado dif�cil. Ya en 1926, los f�sicos Klein y Gordon propusieron una ecuaci�n con esas caracter�sticas que ten�a una forma matem�tica relativamente simple, mas no describ�a adecuadamente los fen�menos cu�nticos. Uno de sus principales defectos era que las part�culas supuestamente descritas pod�an poseer cualquier energ�a, incluso negativa; como todo cuerpo en la naturaleza tiende a pasar, cuando se le deja libre, de un estado de mayor energ�a a otro de menor energ�a, resultar�a que todas las part�culas del Universo tender�an a un estado con energ�a infinitamente negativa, como si cayeran en un pozo sin fondo. Evidentemente, una ecuaci�n que predice tal comportamiento no puede corresponder al mundo real.

El problema de unir adecuadamente la mec�nica cu�ntica y la teor�a de la relatividad parec�a estancado hasta que, en 1930, el f�sico ingl�s Paul Adrian Maurice Dirac logr� deducir una ecuaci�n que describe adecuadamente los fen�menos cu�nticos y es compatible con el principio de la relatividad. Si existe algo as� como una est�tica matem�tica, la ecuaci�n de Dirac es una verdadera obra de arte, por la manera tan ingeniosa con la que el f�sico ingl�s resolvi� un problema aparentemente irresoluble.

Sin entrar en detalles t�cnicos, que rebasar�an los prop�sitos del presente libro, se�alaremos que la ecuaci�n de Dirac permite calcular la funci�n de onda de un electr�n, y de otras part�culas elementales, tomando en cuenta todos los efectos relativistas. Sin embargo, adolec�a del mismo defecto que mencionamos anteriormente: de acuerdo con esta ecuaci�n, un electr�n pod�a tener una energ�a infinitamente negativa. Pero lo que parec�a una dificultad t�cnica result� ser, gracias al ingenio de Dirac, la clave para descubrir un aspecto insospechado de la Naturaleza.

Para evitar que todos los electrones del Universo cayeran a estados con energ�as infinitamente negativas, Dirac propuso que todos los estados con energ�a negativa estaban ocupados ya por electrones, aunque �stos no se puedan detectar directamente (�el vac�o de la mec�nica cu�ntica resulta ser un mar infinito de part�culas!, y esta aparente contradicci�n es todav�a uno de los problemas m�s complejos de la f�sica moderna). Pero si llegara a faltar uno de estos electrones de energ�a negativa, su ausencia, se detectar�a como la presencia de una part�cula con energ�a positiva y con la carga el�ctrica contraria a la del electr�n. Esa nueva part�cula, predijo Dirac, "ser�a un electr�n"; tendr�a la misma masa que un electr�n y todas las dem�s propiedades, excepto el signo de la carga el�ctrica, que ser�a positivo —raz�n por la que esa nueva part�cula fue bautizada positr�n—. M�s a�n, Dirac predijo, con base en su modelo, que al ponerse en contacto un electr�n con un positr�n los dos se aniquilar�an, transformando la totalidad de sus masas en energ�a en forma de dos rayos gamma (fotones de alt�sima energ�a). Adem�s, el argumento de Dirac pod�a aplicarse a cualquier part�cula, por lo que predec�a que existen en la Naturaleza antiprotones, antineutrones, e incluso anti�tomos, compuestos de positrones y antin�cleos.

La hip�tesis de Dirac fue confirmada definitivamente poco tiempo despu�s de haber sido formulada. En 1932, se detectaron positrones en el flujo de rayos c�smicos que llegan a la superficie terrestre, con las caracter�sticas predichas por la teor�a: carga positiva y misma masa que los electrones. Incluso se descubri� posteriormente que algunos elementos radiactivos emiten positrones al decaer sus n�cleos. Y en los a�os cincuenta, cuando empezaron a funcionar los grandes aceleradores de part�culas para estudiar el mundo subat�mico, se logr� producir antiprotones, antineutrones y todo tipo de antipart�culas.

Con las antipart�culas se pueden formar, en principio, anti�tomos, antimol�culas e incluso antimundos —estrellas y planetas, habitados por seres de antimateria—. Los fen�menos naturales en esos antimundos ser�an id�nticos a los que conocemos, con la �nica diferencia de que el signo de todas las part�culas at�micas estar�a invertido; esto se debe a que las leyes de la f�sica son (casi) iguales para la materia y la antimateria.² La apariencia visual de estos antimundos ser�a indistinguible de un mundo de materia, pues la luz (y en general los fen�menos electromagn�ticos) no hace distinci�n entre materia y antimateria. Pero si un d�a nos visitara un ser de antimateria las consecuencias ser�an catastr�ficas para todos: se aniquilar�a totalmente al pisar tierra, produciendo una explosi�n mucho m�s fuerte que una bomba at�mica.

El mecanismo m�s eficiente que existe en la Naturaleza para transformar masa en energ�a es la aniquilaci�n de la materia con la antimateria; la eficiencia del proceso es del 100%, pues la totalidad de la masa se convierte en energ�a en forma de rayos gamma. Desgraciadamente, no es un proceso aprovechable para usos pr�cticos pues no existen yacimientos de antimateria en la Tierra: se pueden producir antipart�culas en los aceleradores de part�culas, a costa de invertir enormes cantidades de energ�a, pero es imposible almacenarlas, pues se aniquilan al menor contacto con la materia.

LAS PART�CULAS (Y ANTIPART�CULAS) ELEMENTALES

A pesar de lo que indica su nombre, un �tomo no es indivisible, sino que est� constituido por electrones que giran alrededor de un n�cleo formado por protones y neutrones. Al principio, los f�sicos pensaron que los elementos b�sicos del Universo eran estas tres part�culas: electr�n, prot�n y neutr�n, y la part�cula de la luz: el fot�n. Pero el n�mero de las part�culas supuestamente elementales empez� a aumentar, primero lentamente y despu�s, en forma alarmante...

Primero, con la teor�a Dirac, aparecieron en la escena los positrones, los antiprotones y los antineutrones. Incluso una part�cula el�ctricamente neutra como el neutr�n tiene su antipart�cula correspondiente. �C�mo distinguir un neutr�n de un antineutr�n, si no tienen carga el�ctrica que los diferencie? La manera m�s simple es ponerlos en contacto: se aniquilan mutuamente produciendo dos fotones extremadamente energ�ticos. En cambio, un fot�n no puede distinguirse de un "antifot�n", pues dos fotones al ponerse en contacto no producen nuevos fotones, sino que prosiguen su existencia sin inmutarse: por esta raz�n, el fot�n es una part�cula que no posee antipart�cula, o dicho m�s precisamente, es indistinguible de ella.

En 1930, surgi� una peque�a alarma por lo que podr�a ser una violaci�n de la ley de conservaci�n de la energ�a y, particularmente, de la f�rmula E = mc². El decaimiento beta es una reacci�n por la cual un neutr�n se transforma en un prot�n, emitiendo un electr�n; esta reacci�n es posible gracias a que la masa del neutr�n es ligeramente superior a la del electr�n, juntos, por lo que la diferencia de masa se transforma en la energ�a para crear el electr�n emitido (Figura 20). Sin embargo, al estudiar el decaimiento beta, los f�sicos se dieron cuenta de que el electr�n resultante pose�a siempre menos energ�a de la que se esperar�a. Se lleg� a sospechar que la f�rmula de Einstein estaba equivocada, pero en 1930 el f�sico Wolfgang Pauli propuso una soluci�n: la energ�a faltante se la llevaba una part�cula hasta entonces desconocida, sin carga el�ctrica y con masa nula o extremadamente peque�a. Tal part�cula fue bautizada neutrino y su existencia fue confirmada varios a�os despu�s, salv�ndose as� la ley de conservaci�n de la energ�a.

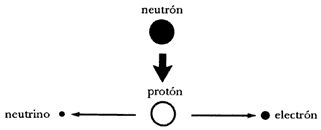
Figura 20. El decaimiento beta: un neutr�n se transforma en un prot�n emitiendo un electr�n y un neutrino.

El neutrino es una part�cula muy curiosa; se sabe en la actualidad que hay por lo menos dos tipos de neutrinos (muy probablemente tres y quiz�s m�s), con sus respectivos antineutrinos. La masa del neutrino parece ser exactamente cero,³ por lo que esta part�cula viaja siempre a la velocidad de la luz, tal como el fot�n. A diferencia de otras part�culas, los neutrinos no tienen ninguna interacci�n con los fotones,⁴ raz�n por la que un neutrino y un antineutrino no se aniquilan al chocar, pues no pueden producir un par de fotones.

�C�mo distinguir entonces un neutrino de un antineutrino, si ninguno tiene carga el�ctrica? La respuesta es muy interesante: el neutrino, al igual que muchas otras part�culas elementales, posee un momento angular, o dicho en palabras m�s simples, gira sobre s� mismo. Lo que distingue un neutrino de un antineutrino es el sentido en el que giran. Esto se ilustra en la figura 21: vistas desde atr�s con respecto a la direcci�n de su movimiento, un neutrino gira en sentido contrario al de las manecillas de un reloj y un antineutrino en el otro sentido.⁵ Sin embargo, podr�amos pensar que si nos movemos m�s r�pido que un neutrino, lo ver�amos moverse en sentido contrario girando como si fuera un antineutrino...�Pero recordemos que los neutrinos se mueven a la velocidad de la luz, por lo que es imposible rebasarlos! Debido al l�mite natural que representa la velocidad de la luz, la distinci�n entre neutrinos y antineutrinos tiene un sentido f�sico muy claro.

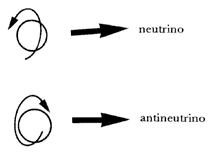
Figura 21. Sentido de rotaci�n de un neutrino y un antineutrino con respecto a la direcci�n de su movimiento.

Otras part�culas siguieron apareciendo en escena. En 1935, el f�sico japon�s Hideki Yukawa propuso la existencia de ciertas part�culas, que llamaron mesones, para explicar la fuerza nuclear entre protones y neutrones. Los mesones fueron descubiertos una d�cada despu�s.

En los a�os cincuenta, los f�sicos hab�an descubierto todo un zool�gico de part�culas elementales con masas muy diversas, aunque casi todas eran inestables y se transformaban r�pidamente en otras part�culas. La �nica regularidad que se pod�a notar entre ellas era la carga el�ctrica, que siempre es un m�ltiplo, positivo o negativo, de la carga del electr�n. Parec�a existir, pues, en la Naturaleza una unidad fundamental de carga el�ctrica:⁶el electr�n posee una unidad negativa y el prot�n una unidad positiva; los mesones pueden tener tanto carga positiva como negativa; algunas part�culas como el neutr�n, el neutrino y el fot�n, poseen carga cero, mientras que otras part�culas m�s raras tienen dos o m�s unidades de carga.

Para poner un poco de orden en la familia de las part�culas elementales, el f�sico estadounidense Murray Gell-Mann sugiri� en los a�os sesenta que las part�culas como los mesones, protones, neutrones y otras m�s pesadas est�n constituidas por part�culas a�n m�s elementales, a las que bautiz� cuarks. La carga de los cuarks debe ser un tercio o dos tercios de la unidad fundamental de carga, con lo que se pueden explicar las propiedades b�sicas de las part�culas elementales: Por ejemplo, el prot�n est� formado por dos cuarks con carga +2/3 y uno con carga -1/3, dando una carga neta igual a una unidad; el neutr�n consta de dos cuarks con carga -1/3 y uno con carga +2/3, siendo la carga total nula; en cuanto a los mesones, est�n formados por parejas de cuarks y anticuarks, por lo que se desintegran r�pidamente en el estado libre.

El modelo propuesto por Gell-Mann era muy ingenioso, y muchos datos experimentales lo confirmaban, excepto el hecho de que nadie pod�a detectar un cuark. Durante a�os, los f�sicos trataron de encontrar cuarks aislados en estado natural, sin tener �xito, hasta que se dieron cuenta de que los cuarks no pueden existir solos. La raz�n es que los cuarks se encuentran unidos entre si con una fuerza enorme que, adem�s, aumenta con la distancia. Al contrario de la fuerza el�ctrica o la gravitacional —que disminuyen al aumentar la distancia entre los cuerpos que se atraen— los cuarks est�n ligados entre s� por una interacci�n que aumenta con la separaci�n, tal como un resorte que, mientras m�s se estira, atrae con mayor fuerza.

La analog�a del resorte puede ilustrar la raz�n por la que los cuarks no existen aislados. Supongamos que queremos separar dos cuarks ligados entre s�; podemos estirar el "resorte" que los une m�s y m�s hasta que se rompe. Pero para romper un resorte, hay que invertir energ�a. En el caso de los cuarks esta energ�a es tan grande que puede transformarse en la masa de dos nuevos cuarks. El resultado es que, al romperse el "resorte", se producen dos parejas de cuarks en lugar de dos cuarks aislados, tal como se ilustra en la figura 22.

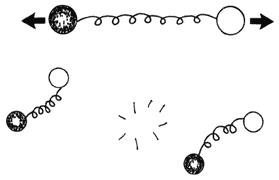
Figura 22. La interacci�n entre los cuarks es an�loga a un resorte. La energ�a almacenada en el resorte permite crear un par de cuarks.

Hoy en d�a, los f�sicos piensan que los constituyentes b�sicos de la materia son los cuarks, por una parte, y los llamados leptones (part�culas ligeras como el electr�n y el neutrino) por la otra. �stas se estudian en los aceleradores de part�culas, donde alcanzan velocidades muy cercanas a la de la luz, gracias a las enormes cantidades de energ�as invertidas. Al chocar entre s�, las part�culas forman nuevas part�culas. La comprensi�n de estos fen�menos ha sido posible gracias a la uni�n de las dos grandes teor�as de la f�sica moderna.