II. �TER, LUZ Y ELECTROMAGNETISMO
ADEM�S de la mec�nica, la otra gran contribuci�n de Newton a la
f�sica es la �ptica, el estudio de la luz. De hecho, uno de sus primeros trabajos
cient�ficos fue analizar la luz que pasa por un prisma y descubrir que la luz
blanca est� compuesta, en realidad, de una mezcla de todos los colores del arco
iris. Unos veinte a�os despu�s de la publicaci�n de los Principios matem�ticos,
Newton public� su segundo libro: �ptica, dedicado casi exclusivamente
al fen�meno de la luz. La descomposici�n de la luz en sus colores primarios
y la trayectoria de los rayos luminosos a trav�s de lentes transparentes fueron
estudiadas exhaustivamente por Newton y sus contempor�neos. Sin embargo, quedaba
pendiente de comprender la naturaleza misma de la luz.
�Qu� es la luz? El mismo Newton pensaba que la luz est� constituida por part�culas que se mueven en el espacio a gran velocidad, como proyectiles, rebotando o absorbi�ndose en los cuerpos materiales, o penetrando en los cuerpos transparentes, como el vidrio. Otros notables f�sicos de esa �poca, como el holand�s Huygens, pensaban que la luz era una onda, an�loga a las olas en el agua o al sonido en el aire. Pero, si la luz es realmente una onda, es decir una vibraci�n de alg�n medio, �cu�l es el equivalente del agua o del aire?, �qu� medio transporta a una onda luminosa? Evidentemente, ese medio deber�a ser el �ter, esa sustancia que llena y permea todo el Universo. Una vez m�s era necesario invocar al �ter, fen�meno f�sico, aunque no existiera ninguna observaci�n directa de tan misteriosa sustancia.
La controversia sobre la naturaleza de la luz —part�cula u onda— persisti� a�n despu�s de Newton y Huygens, hasta que en el siglo XIX la balanza se inclin�, al parecer definitivamente, a favor de la teor�a ondulatoria (victoria ef�mera, como veremos m�s adelante).
El avance m�s trascendental de la f�sica del siglo pasado lo constituy�, sin duda, la comprensi�n de los fen�menos el�ctricos y magn�ticos y su relaci�n con la luz, lo que abri� las puertas a la f�sica moderna e hizo posible la teor�a de la relatividad.
La gravitaci�n no es la �nica fuerza que act�a a distancia. Tambi�n los cuerpos cargados el�ctricamente se atraen o se repelen, y asimismo los imanes interact�an entre s� o con el hierro.
En el siglo XVIII, el f�sico franc�s Coulomb demostr� que dos cuerpos el�ctricamente cargados ejercen una fuerza de atracci�n o repulsi�n entre s� similar a la fuerza gravitacional: proporcional a la magnitud de la carga e inversamente proporcional al cuadrado de la distancia entre ellas. Pero, a diferencia de la fuerza gravitacional, que siempre es atractiva la fuerza el�ctrica puede ser repulsiva o atractiva, si las cargas de los cuerpos son del mismo signo o de signo contrario. (Existen en la naturaleza cargas el�ctricas positivas y negativas: por ejemplo, un �tomo est� constituido por un n�cleo con carga positiva, rodeado de electrones de carga negativa; en condiciones normales, las dos cargas se compensan exactamente entre s� y la carga total de un �tomo es cero.)
Aproximadamente por la misma �poca, Benjamin Franklin, en Estados Unidos, demostr� que los rayos que se producen durante las tormentas son gigantescas chispas el�ctricas que saltan entre las nubes y el suelo.
El estudio de la electricidad cobr� un auge muy especial cuando se inventaron las pilas, que en un principio se consideraron botellas que contienen un misterioso "fluido el�ctrico". Las pilas producen una corriente el�ctrica en un cable de metal; hoy en d�a, sabemos que la corriente el�ctrica es efectivamente un flujo de part�culas llamadas electrones.
El hecho de que el magnetismo est� relacionado con la electricidad se hizo evidente cuando el f�sico dan�s Hans Christian Oersted descubri�, a principios del siglo XIX, que las corrientes el�ctricas producen fuerzas magn�ticas que influyen sobre los imanes: una br�jula tiende a alinearse perpendicularmente a un cable por donde pasa una corriente el�ctrica suficientemente fuerte. Posteriormente, el cient�fico franc�s Jean-Marie Ampère encontr� una ley que relaciona la corriente el�ctrica con la fuerza magn�tica que genera.
Pero el fen�meno m�s importante que pone de manifiesto la relaci�n entre electricidad y magnetismo fue descubierto por el f�sico ingl�s Michael Faraday en 1831. Faraday not� que el movimiento de un im�n puede inducir una corriente el�ctrica en un cable, sin necesidad de pilas. En su �poca, este fen�meno parec�a tener poca importancia, pero un siglo despu�s el efecto de Faraday sirvi� para generar y utilizar la energ�a el�ctrica.
Tal era la situaci�n de la electricidad y el magnetismo hasta mediados del siglo XIX: una serie de fen�menos y leyes aislados que relacionaban entre s� la electricidad y el magnetismo. Hac�a falta una formulaci�n unificada de estas leyes que permitiera una comprensi�n m�s profunda de la naturaleza de estas fuerzas. Tal obra fue realizada por Maxwell.
James Clerk Maxwell (Figura 5) naci� en 1831, en Escocia. Su primera incursi�n en la f�sica fue un estudio te�rico de la estabilidad de los anillos del planeta Saturno: demostr� que �stos no pod�an ser cuerpos s�lidos, ya que la fuerza gravitacional del planeta los romper�a con rapidez. Posteriormente, se interes� en la teor�a molecular de los gases y lleg� a ser uno de los pioneros de la llamada f�sica estad�stica. Pero su obra m�s importante consiste en la formulaci�n matem�tica de las leyes del electromagnetismo, los fen�menos unificados de la electricidad y el magnetismo. Maxwell logr� expresar las leyes descubiertas por Coulomb, Faraday y Ampère en un conjunto de f�rmulas (ecuaciones diferenciales, en lenguaje t�cnico) que relacionan matem�ticamente las distribuciones de cargas y corrientes con las fuerzas el�ctricas y magn�ticas que generan en cada punto del espacio.
Figura 5. James Clerk Maxwell (1831-1879).
Las ecuaciones de Maxwell permitieron ver en forma clara que la electricidad y el magnetismo son dos manifestaciones de un mismo fen�meno f�sico, el electromagnetismo. El fen�meno era similar a la gravitaci�n, cuyas leyes fueron descubiertas por Newton; as� como un cuerpo masivo produce una fuerza gravitacional sobre otro, un cuerpo el�ctricamente cargado y en movimiento produce una fuerza electromagn�tica sobre otro cuerpo cargado. La diferencia m�s importante es que la magnitud y la direcci�n de la fuerza electromagn�tica dependen de la carga del cuerpo que lo produce y tambi�n de su velocidad; por esta raz�n, la teor�a del electromagnetismo es m�s complicada que la teor�a newtoniana de la gravitaci�n, y las ecuaciones de Maxwell son m�s complejas que la f�rmula de Newton para la fuerza gravitacional.
Un aspecto com�n entre la gravitaci�n y el electromagnetismo es la existencia de una aparente acci�n a distancia entre los cuerpos, acci�n que tanto disgustaba a Newton. Maxwell no resolvi� ese problema, pero invent� un concepto que desde entonces se ha utilizado constantemente en la f�sica: el campo electromagn�tico. Seg�n esta interpretaci�n, en todo punto del espacio alrededor de una carga existe una fuerza electromagn�tica, cuya intensidad y direcci�n est�n definidas por medio de unas f�rmulas matem�ticas. En realidad, m�s que un concepto, el campo es una definici�n que da cierta consistencia a la idea de que una carga el�ctrica act�a sobre otra lejana, sin tener que recurrir a una acci�n a distancia. S�lo en el siglo XX se pudo encontrar cierta base f�sica a este concepto, pero en tiempos de Maxwell el campo electromagn�tico era una noci�n matem�tica sumamente �til, descrita por ecuaciones, pero cuya realidad f�sica trascend�a toda interpretaci�n te�rica.
El primer �xito, y el m�s notable, de la teor�a de Maxwell fue la elucidaci�n de la naturaleza de la luz. Maxwell demostr�, a partir de sus ecuaciones matem�ticas, que la luz es una onda electromagn�tica que consiste en oscilaciones del campo electromagn�tico. As� quedaba establecida, m�s all� de cualquier duda, la naturaleza ondulatoria de la luz, tal como lo pensaba Huygens y en contra de la opini�n de Newton.
Se llama longitud de onda la distancia entre las dos crestas de una onda (Figura 6). En el caso de una onda de luz, esta longitud determina el color: a la luz roja corresponde una longitud de onda de ocho diezmil�simas de mil�metro, mientras que a la luz violeta le corresponde una longitud de cuatro diezmil�simas de mil�metro; en el intervalo comprendido entre estas dos longitudes se encuentran todas las gamas de colores del arco iris. Pero el ojo humano s�lo puede percibir un intervalo muy peque�o de ondas luminosas. M�s all� de la luz violeta se encuentra la llamada luz ultravioleta, luego los rayos X y finalmente los rayos gamma, cada uno con longitudes de onda cada vez m�s cortas. En el otro lado, con longitudes de onda cada vez mayores que la luz roja, se encuentra la luz infrarroja, las microondas y las ondas de radio.
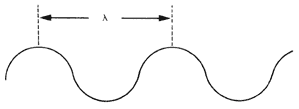
Figura 6. La longitud de onda.
Pero �qu� sustenta a una onda en el espacio? Este problema no parec�a haber avanzado m�s all� de las primeras suposiciones de Newton. No qued� m�s recurso a Maxwell que recurrir a la existencia del misterioso �ter como un medio f�sico que transporta las ondas electromagn�ticas y da cierto sustento al concepto del campo. Pero el problema del �ter estaba relacionado con otro aspecto, enigm�tico, de la teor�a de Maxwell: la aparente necesidad de un espacio absoluto.
Como mencionamos en el cap�tulo anterior, las leyes de la f�sica deben ser independientes de todo sistema de referencia, de acuerdo con el principio de relatividad de Galileo. Sin embargo, las leyes del electromagnetismo, tal como las planteaba Maxwell, no cumpl�an este principio: al pasar de un sistema de referencia a otro, las ecuaciones de Maxwell tomaban una forma distinta, lo que implicaba leyes de la f�sica diferentes. De hecho las ecuaciones del electromagnetismo en la forma deducida por Maxwell s�lo pod�an ser v�lidas en un sistema de referencia muy especial, y los f�sicos especularon que �se no pod�a ser otro que el espacio absoluto.
Como mencionamos en el cap�tulo anterior, las leyes de la f�sica deben ser independientes de todo sistema de referencia, de acuerdo con el principio de relatividad de Galileo. Sin embargo, las leyes del electromagnetismo, tal como las planteaba Maxwell, no cumpl�an este principio: al pasar de un sistema de referencia a otro las ecuaciones de Maxwell tomaban una forma distinta, lo que implicaba leyes de la f�sica diferentes. De hecho las ecuaciones del electromagnetismo en la forma deducida por Maxwell s�lo pod�an ser v�lidas en un sistema de referencia muy especial, y los f�sicos especularon que �se no pod�a ser otro que el espacio absoluto.
Ilustremos lo anterior con un ejemplo simple: el campo magn�tico act�a sobre una part�cula cargada si �sta se encuentra en movimiento: la fuerza ejercida es directamente proporcional a la velocidad (y perpendicular a la direcci�n del movimiento). De acuerdo con la ley de Amp�re, una corriente el�ctrica produce un campo magn�tico, el cual puede actuar sobre una part�cula cargada que se mueve paralelamente a la corriente; se puede ver que la part�cula es atra�da hacia el cable conductor con una fuerza proporcional a su velocidad (Figura 7). Pero �qu� pasa en un sistema de referencia que se mueve junto con la part�cula cargada? En ese sistema, la part�cula est� en reposo y, por lo tanto, la corriente el�ctrica no debe ejercer ninguna fuerza sobre ella, ya que el campo magn�tico no act�a sobre part�culas en reposo. Este es un claro ejemplo de la no-invariancia de las leyes f�sicas con respecto al sistema de referencia: aparentemente, hemos llegado al resultado contradictorio de que una part�cula es atra�da por una corriente el�ctrica seg�n desde donde la miremos. La �nica soluci�n evidente de la paradoja es postular que las leyes del electromagnetismo tienen una forma muy especial en un cierto sistema de referencia privilegiado, cuya existencia objetiva se puede determinar por medio de experimentos f�sicos. Por ejemplo, en el caso de la part�cula que se mueve a lo largo de una corriente el�ctrica, debe influir no s�lo la velocidad de la part�cula con respecto al cable, sino tambi�n su velocidad con respecto a ese sistema de referencia privilegiado.
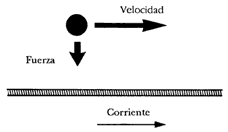
Figura 7. Una part�cula cargada en movimiento resiente una fuerza de atracci�n (o repulsi�n) producida por una corriente el�ctrica.
La existencia de un sistema de referencia absoluto es perfectamente aceptable si uno admite la realidad del �ter como una sustancia universal que sustenta los fen�menos electromagn�ticos. El sistema absoluto es aqu�l donde el �ter est� en reposo y debe coincidir con el sistema de referencia en el que las estrellas, en promedio, parecen estar fijas. De hecho, la manera m�s directa de determinar la velocidad de un sistema de referencia con respecto al �ter es medir la velocidad de la luz. Siendo esta velocidad definida con respecto al �ter en reposo, debe variar de acuerdo con la velocidad del sistema de referencia.
Este hecho se utiliz� en el primer intento de medir la velocidad de la Tierra en el �ter, como veremos. As�, el espacio absoluto parecer�a tener una realidad f�sica, m�s all� de la necesidad subjetiva de que exista un punto de referencia en el Universo con respecto al cual se puedan definir en forma �nica todos los movimientos.
La situaci�n en el siglo pasado era tal que ning�n f�sico dudaba de la existencia del �ter, pero nadie ten�a la m�s remota idea de qu� clase de sustancia pod�a ser. Si todo lo penetraba sin que nada pudiera influir sobre �l, �c�mo detectarlo? Se pensaba que la �nica posibilidad real de confirmar, aun indirectamente, su existencia era a trav�s de experimentos con la luz.
Si la luz tiene una velocidad bien definida con respecto al �ter, entonces esta velocidad debe variar seg�n el movimiento de quien la mida. Si un barco se mueve con una cierta velocidad fija con respecto al agua en reposo, ese mismo barco navegando por un r�o se mover� con respecto a la tierra firme con mayor o menor velocidad seg�n si sube o baja la corriente. Para un observador en tierra firme, la velocidad del barco ser� menor si se mueve r�o arriba porque hay que restar la velocidad del agua a la del barco, mientras que si el barco se mueve r�o abajo, las dos velocidades se adicionan.
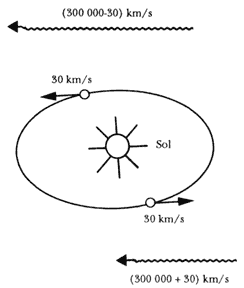
Figura 8. La velocidad de la luz deber�a variar seg�n la direcci�n de un rayo luminoso, debido al movimiento de la tierra.
Lo mismo debe suceder con la luz, cuya velocidad es fija con respecto al �ter. La Tierra gira alrededor del Sol con una velocidad aproximada de 30 kil�metros por segundo. De acuerdo con el razonamiento anterior, un rayo de luz emitido en el sentido de movimiento de la Tierra debe moverse, con respecto a la Tierra misma, con una velocidad menor que un rayo emitido en la direcci�n contraria, siendo la diferencia de velocidades entre los dos rayos luminosos de 60 kil�metros por segundo (Figura 8). Si se pudiera medir esa variaci�n de la velocidad se confirmar�a indirectamente la existencia del �ter, o al menos la de un sistema de referencia absoluto.
La velocidad de la luz es de aproximadamente 300 000 kil�metros por segundo; evidentemente, la medici�n de la velocidad luminosa debe ser extremadamente precisa para poder detectar una variaci�n de s�lo 60 kil�metros por segundo. Tal era el reto para los f�sicos experimentales del siglo pasado.
El primer experimento confiable para medir la velocidad de la Tierra con respecto
al �ter fue realizado en 1887 por los norteamericanos Albert Abraham Michelson
y Edward W. Morley El aparato que utilizaron fue un interfer�metro, que permite
medir distancias y velocidades con enorme precisi�n utilizando haces de luz
en interacci�n.1 ![[Nota 1]](../imgs/mcommnt.gif){kind=small}
El
experimento consist�a en dividir, por medio de un espejo semitransparente, un
haz luminoso en dos haces perpendiculares, que se reflejaban en sendos espejos
para volver a unirse y calibrar, as�, el aparato. Luego se giraba todo el aparato:
cualquier cambio en la velocidad de la luz deber�a producir una interferencia
entre los dos haces luminosos que pod�a detectarse directamente (Figura 9).
Figura 9. El interfer�metro utilizado por Michelson y Morley.
El experimento se llev� a cabo con todo el cuidado necesario, pero, sorprendentemente, Michelson y Morley no detectaron ning�n cambio en la velocidad de la luz. A pesar del movimiento de la Tierra, la luz se mov�a con la misma velocidad en todas las direcciones.
�C�mo explicar el resultado negativo del experimento? Tanto Michelson y Morley, como otros f�sicos, propusieron varias hip�tesis: quiz�s la Tierra arrastra consigo al �ter en su movimiento; quiz�s los cuerpos se contraen en la direcci�n de su movimiento, cancelando as� el efecto debido a la diferencia de velocidades de los dos haces luminosos del experimento; quiz�s la velocidad de la luz es constante con respecto a la fuente que la emite, etc. Durante algunas d�cadas, el resultado negativo del experimento de Michelson-Morley fue uno de esos detalles molestos que no encajan en ninguna teor�a bien establecida, y que no cobran verdadera importancia hasta que se produce una revoluci�n cient�fica. En este caso, la revoluci�n cient�fica fue la teor�a de la relatividad.
