III. LA RELATIVIDAD DE EINSTEIN

ALBERT EINSTEIN naci� en 1879 en la ciudad alemana de Ulm. Seg�n contaba �l mismo, empez� a interesarse en la f�sica siendo a�n ni�o, un d�a que le compraron una br�jula. Le intrigaba el hecho de que el im�n se�alara siempre la misma direcci�n, y, como era de esperarse, las explicaciones que le dieron los adultos estaban lejos de satisfacerle.

Cuando lleg� a la edad de escoger profesi�n, Einstein decidi� estudiar f�sica en el Instituto Tecnol�gico de Zurich, a donde logr� ingresar no sin haber sido rechazado en su primer intento por tener calificaciones mediocres en todas las materias, excepto en matem�ticas. En �se Instituto se graduar�a finalmente en 1900.

Figura 10. Albert Einstein en la oficina de patentes de Berna, alrededor de 1905.

Como no hab�a sido un estudiante brillante, Einstein no logr� encontrar ning�n puesto de trabajo como f�sico al terminar sus estudios. Finalmente, para subsistir y mantener a su familia (se hab�a casado en 1903 y su primer hijo hab�a nacido poco despu�s), acept� un empleo en la Oficina de Patentes de Berna, en Suiza. Su trabajo consist�a en estudiar las solicitudes de patentes, pero en sus ratos libres segu�a dedic�ndose a la f�sica.

Uno de los problemas que m�s le interesaba en aquella �poca era la aparente incompatibilidad entre el principio de relatividad galileano y la teor�a electromagn�tica de Maxwell. Sobre este tema, y antes de Einstein, hab�an trabajado el f�sico holand�s Hendrik Lorentz y el matem�tico franc�s Henri Poincar�. El problema que se hab�an planteado era el siguiente: Las ecuaciones de Maxwell describen el comportamiento del campo electromagn�tico en cada punto del espacio y en cada instante de tiempo (o, en t�rminos un poco m�s matem�ticos, dicho campo depende de tres coordenadas espaciales, digamos x, y, z, y el tiempo t) Ahora bien �se pueden cambiar la posici�n y el tiempo en las ecuaciones de Maxwell sin alterar su forma? En el caso de las ecuaciones de la mec�nica newtoniana, la respuesta es afirmativa debido al principio de relatividad de Galileo: se puede pasar de un sistema de referencia a otro sin cambiar la forma de las ecuaciones (las leyes de la f�sica son invariantes), si el tiempo medido en cada sistema es el mismo. Evidentemente, en el caso del electromagnetismo, el problema es m�s complicado porque, no se puede recurrir a la relatividad galileana. Sin embargo, Lorentz demostr� que existe una transformaci�n matem�tica que deja invariante la forma de las ecuaciones de Maxwell, siempre y cuando se cambie no s�lo la posici�n de un punto sino tambi�n el tiempo. El mismo resultado fue obtenido y generalizado por Poincar�. (Ver Ap�ndice).

En su �poca, el trabajo de Lorentz fue considerado una curiosidad matem�tica, ingeniosa pero desprovista de sentido f�sico. En efecto; �c�mo puede el tiempo transcurrir en forma diferente en sistemas de referencia distintos? La misma experiencia diaria y el sentido com�n parecen negar tal posibilidad.

Tal era la situaci�n cuando Einstein public� en 1905 el famoso art�culo intitulado Sobre la electrodin�mica de los cuerpos en movimiento, en una prestigiosa revista alemana de f�sica; con ese trabajo naci� la teor�a de la relatividad.

Einstein postul� que las ecuaciones de Maxwell deben tener la misma forma en cualquier sistema de referencia inercial y que, por lo tanto, es imposible distinguir, a partir de experimentos electromagn�ticos, un sistema de referencia inercial de otro. Para que este principio de relatividad se cumpla, es necesario que las transformaciones de Lorentz sean f�sicamente v�lidas; en consecuencia, el tiempo medido entre dos sucesos depende del movimiento de quien lo mide.

Einstein postul� que no existe un tiempo absoluto, ni un espacio absoluto y, por lo tanto, tampoco un �ter. Pero, si no existe el �ter �con respecto a qu� debe medirse la velocidad de la luz? La respuesta fue tajante: la velocidad de la luz (en el vac�o) es la misma en cualquier sistema de referencia inercial. Despu�s de todo, eso es lo que indic� el experimento de Michelson y Morley.

La invariancia de la velocidad de la luz parece contradecir toda experiencia. Si la velocidad de la luz es de 300 000 kil�metros por segundo, se esperar�a que al correr tras una se�al luminosa �sta parecer�a tener una velocidad menor. Sin embargo, seg�n Einstein, no importa c�mo se mueva un sistema de referencia, pues la velocidad de la luz medida en �l ser� siempre de 300 000 kil�metros por segundo. En la teor�a de la relatividad, las velocidades no se adicionan o sustraen simplemente, pues hay que tomar en cuenta tambi�n c�mo se mide el tiempo en un sistema de referencia dado. (Ver Ap�ndice A. )

En resumen, la velocidad de la luz en el vac�o¹ es una constante fundamental de la naturaleza, independiente de qui�n la mida. Es una velocidad extremadamente alta en comparaci�n con nuestra experiencia cotidiana (un rayo luminoso s�lo necesita dos segundos para ir de la Tierra a la Luna y volver). �Por qu� la luz tiene esa velocidad y no otra? Esta pregunta no la puede responder la f�sica; lo �nico que se puede afirmar es que, de ser otra la velocidad de la luz, el Universo ser�a muy distinto al que conocemos y no existir�amos nosotros para formularnos tales preguntas.

EL TIEMPO Y EL ESPACIO RELATIVOS

El hecho de que el tiempo no transcurre en forma igual para observadores distintos es una de las predicciones m�s sorprendentes de la teor�a de Einstein. Nuestro sentido com�n, basado en la pr�ctica cotidiana, indica que los relojes funcionan de la misma forma, sin importar c�mo se mueven. �No es entonces absurdo pretender que el tiempo medido es relativo al observador? Es importante se�alar que el efecto predicho por Einstein s�lo es perceptible a velocidades cercanas a la de la luz.

Para ser m�s precisos, supongamos que, en un cierto sistema de referencia, dos sucesos ocurren en el mismo lugar y con un intervalo de tiempo t. En otro sistema de referencia que se mueve con velocidad V con respecto al primero, los dos sucesos ocurren con un intervalo de tiempo t' dado por la f�rmula:

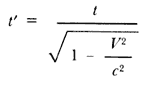
( de aqu� en adelante usaremos c para designar la velocidad de la luz); es decir, el tiempo medido en el segundo sistema es mayor que el medido en el primero. Qu� tan mayor depende de la velocidad V; si V es muy peque�a con respecto a la velocidad de la luz c, entonces la diferencia entre t y t' es pr�cticamente imperceptible (por ejemplo, si V=10 000 kil�metros por hora, t y t' apenas difieren en una parte en cien mil millones); en el otro extremo, si V es cercano a la velocidad de la luz, entonces es mucho mayor que t (por ejemplo, si V es 0.997 veces la velocidad de la luz, entonces t' es 13 veces mayor que t). La relaci�n entre los tiempos medidos en dos sistemas de referencia en movimiento relativo est� determinada por el valor del llamado factor de Lorentz:

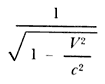
que difiere del valor 1 s�lo para velocidades cercanas a la de la luz (Figura 11).

As�, la raz�n por la que no percibimos variaciones de tiempo en nuestra experiencia diaria es que estamos acostumbrados a movernos a velocidades extremadamente peque�as con respecto a la velocidad de la luz. Si la velocidad de la luz fuera much�simo menor de lo que es, estar�amos acostumbrados a variaciones del tiempo, y no hubiera sido necesario un Einstein para convencernos de que el tiempo es relativo a quien lo mide.

Pero entonces, �es imposible determinar en forma �nica la duraci�n de un fen�meno?, �nos condena la relatividad a perder el concepto del tiempo? Nada de eso. El tiempo que marca un reloj es un concepto perfectamente bien definido. De acuerdo con la teor�a de la relatividad, el tiempo de ese reloj no coincide con el que marca otro reloj que se mueve con respecto al primero, pero la relaci�n entre los dos tiempos se puede determinar perfectamente.

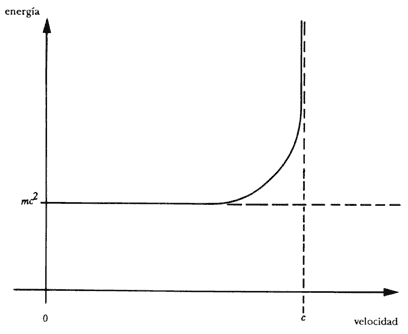
Figura 11. Gr�fica del factor de Lorentz g en funci�n de la velocidad v.

Todos los fen�menos f�sicos tienen su tiempo asociado: los relojes de cuarzo que se utilizan en la actualidad miden el tiempo contando el n�mero de vibraciones electromagn�ticas emitidas por los �tomos en un cristal de cuarzo, y ese tiempo es el mismo para todos los relojes del mundo. Si un cosmonauta realizara un viaje por el espacio a una velocidad cercana a la de la luz, no percibir�a nada de particular con respecto a su propio tiempo, pero al regresar a la Tierra notar�a que su reloj no coincide con el de los que se quedaron en ella. Como veremos m�s detalladamente en el siguiente cap�tulo, el tiempo transcurrido para el cosmonauta ser� menor que el transcurrido en la Tierra, aunque ambos tiempos se pueden medir sin ambig�edades.

En conclusi�n, si queremos medir el tiempo transcurrido entre dos sucesos, nos conviene hacerlo en un sistema de referencia en el que los dos sucesos ocurren en el mismo punto. Al tiempo as� medido, los f�sicos llaman tiempo propio. En otro sistema de referencia que se mueve con respecto al primero, los dos sucesos no parecen ocurrir en el mismo sitio y el tiempo transcurrido entre ellos difiere del tiempo propio por un factor de Lorentz. (Figura 11.)

Otra consecuencia sorprendente de la teor�a de Einstein es que el espacio, al igual que el tiempo, tambi�n es relativo a quien lo mide. M�s espec�ficamente, si la longitud de un cuerpo en reposo es L, entonces su tama�o en movimiento, digamos L', ser� menor, de acuerdo con la f�rmula:

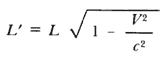
Tal y como sucede con el tiempo, esta contracci�n aparente es imperceptible si la velocidad del objeto es mucho menor que la velocidad de la luz.

Es importante, sin embargo, no confundir esta contracci�n del tama�o con la apariencia visual de un objeto en movimiento. Cuando vemos un objeto, percibimos en cada instante la luz que fue emitida por distintas partes del cuerpo a tiempos distintos, porque la luz no se propaga instant�neamente. Este efecto debe tomarse en cuenta, en combinaci�n con la contracci�n mencionada m�s arriba, para deducir la apariencia de un cuerpo en movimiento. Volveremos a este tema en el siguiente cap�tulo.

MATERIA Y ENERG�A

Adem�s de la contracci�n del tiempo y del espacio, la teor�a de la relatividad predice un efecto que, en un principio, parec�a un resultado puramente formal, pero que algunos a�os m�s tarde modific� fundamentalmente el curso de la historia. Einstein se dio cuenta de que la masa y la energ�a de un cuerpo aparecen siempre unidas de una manera muy conspicua en las ecuaciones de su teor�a. Esto le condujo a afirmar que existe una equivalencia entre la masa y la energ�a expresada por la f�rmula:

donde E es la energ�a de un cuerpo, m su masa y c² la velocidad de la luz elevada al cuadrado.

En la mec�nica newtoniana, un cuerpo de masa m que se mueve con velocidad V posee, en virtud de su movimiento, una energ�a igual a 1/2 mV². En la teor�a de la relatividad, la energ�a de movimiento del cuerpo resulta ser:

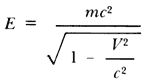
donde una vez m�s aparece el factor de Lorentz. Lo interesante de esta f�rmula es que, incluso cuando un cuerpo se encuentra en reposo (es decir, V = 0), posee una energ�a que es justamente mc². Einstein concluy� que un cuerpo aun en reposo posee una energ�a almacenada en forma de masa.

La f�rmula de Einstein E = mc² afirma que un solo kilogramo de materia equivale aproximadamente a toda la energ�a que se consume en la Tierra en una hora. Obviamente surge la pregunta de si se puede extraer, en la pr�ctica, la enorme energ�a almacenada en la materia. Al principio Einstein y los dem�s f�sicos pensaban que eso era s�lo una ilusi�n; pero la situaci�n empez� a cambiar en los a�os treinta...

Algunas veces, la f�rmula de Einstein se interpreta en el sentido de que un cuerpo que se mueve aumenta su masa, adquiriendo una nueva masa m' dada por la f�rmula:

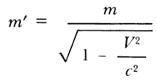
Sin embargo, es m�s conveniente interpretar esto como un aumento de energ�a del cuerpo, ya que en la pr�ctica, la masa de un cuerpo en movimiento no se puede medir sin ambig�edades.

Por �ltimo, hay que notar que seg�n la f�rmula anterior la energ�a de un cuerpo aumenta indefinidamente a medida que su velocidad v tiende a la velocidad luminosa (recu�rdese el factor Lorentz, Figura 11). Para que un cuerpo alcance la velocidad de la luz, se necesita una energ�a infinita. Por esta raz�n, la velocidad de la luz es una barrera natural a todas las velocidades en la naturaleza: todo cuerpo masivo est� restringido a moverse m�s lentamente que la luz.

LA NATURALEZA DE LA LUZ

Como se�alamos anteriormente, la teor�a de la relatividad cort� de ra�z el concepto del �ter como sistema absoluto de referencia. Fue un alivio para la f�sica, pues no hab�a modo de explicar la naturaleza de una sustancia tan intangible. Sin embargo, al desaparecer el �ter resurg�a con m�s fuerza el problema de la propagaci�n de la luz: si la luz es una onda, como indican todos los experimentos, �en qu� medio se propaga? Para responder a esta pregunta, fue necesaria otra revoluci�n cient�fica: la mec�nica cu�ntica, en cuya fundaci�n tambi�n particip� Einstein en forma decisiva.

Todo cuerpo caliente radia energ�a en forma de luz; por ejemplo, un hierro incandescente emite principalmente luz roja, pero tambi�n luz de otras longitudes de onda. La cantidad de energ�a emitida en cada longitud de onda depende fundamentalmente de la temperatura del cuerpo emisor y se puede medir experimentalmente. A fines del siglo XIX, los f�sicos se enfrentaban al problema de explicar te�ricamente lo que observaban en el laboratorio, pero algo parec�a no funcionar con los conceptos bien establecidos de la f�sica.

Finalmente, el f�sico alem�n Max Planck demostr� que se pod�a explicar la forma de la radiaci�n emitida por un cuerpo si se postulaba, que la luz se propaga en paquetes de energ�a, siendo la energ�a de cada paquete inversamente proporcional a la longitud de la onda. De acuerdo con la hip�tesis de Planck, la energ�a transportada por una onda luminosa es un m�ltiplo de la energ�a:

hv

donde h es la llamada constante de Planck —su valor es 6.547 X 10^-27 erg/seg— y v, es, la frecuencia de la onda (el n�mero de vibraciones por segundo; la frecuencia v y la longitud de onda l est�n relacionadas por la f�rmula v=c/l).

La hip�tesis de Planck, formulada en 1900, explicaba los experimentos pero no parec�a tener ninguna base f�sica. Despu�s de todo, una onda luminosa puede tener cualquier energ�a, del mismo modo como una onda de sonido puede ser d�bil o fuerte. En 1916 Einstein propuso una soluci�n revolucionaria; �la luz est� compuesta de part�culas!, siendo la energ�a de cada part�cula hv; de acuerdo con la hip�tesis de Planck.

Una vez m�s, Einstein contradec�a las ideas bien establecidas de su �poca. Cuando finalmente los f�sicos se hab�an convencido de que la luz es una onda, �Einstein postulaba que es una part�cula! Sin embargo, esta dualidad onda-part�cula result� ser una propiedad fundamental de la naturaleza a nivel at�mico. Todos los fen�menos at�micos est�n regidos por la mec�nica cu�ntica, que es radicalmente distinta de la mec�nica newtoniana. Uno de los postulados b�sicos de la mec�nica cu�ntica es que las part�culas elementales, que constituyen la materia, est�n dotadas de propiedades tanto de onda como de part�cula.

La part�cula de la luz es el fot�n, que tambi�n se comporta como una onda, y la relaci�n entre la energ�a del fot�n y su frecuencia est� dada por la f�rmula de Planck. Evidentemente, el fot�n viaja siempre a la velocidad de la luz. Para ello, su masa debe ser exactamente cero, ya que, como se�alamos m�s arriba, una part�cula masiva necesita energ�a infinita para moverse a la velocidad de la luz; s�lo una part�cula sin masa puede viajar a esa velocidad y poseer una energ�a finita.

Einstein postul� la existencia del fot�n en otro famoso art�culo publicado en 1905, en el que explicaba el efecto fotoel�ctrico. Este fen�meno consiste en que algunos materiales producen una corriente el�ctrica al absorber la luz, lo cual es el principio del funcionamiento de las celdillas fotoel�ctricas; muy utilizadas actualmente (para hacer que cierre la puerta de un elevador, por ejemplo). El trabajo de Einstein sobre el efecto fotoel�ctrico (y no la teor�a de la relatividad) le vali� el premio N�bel de f�sica de 1921.

Por supuesto, el fot�n no necesita de ning�n �ter para propagarse. En el lenguaje de la f�sica moderna, el campo electromagn�tico posee energ�a, y esta energ�a est� cuantizada: aparece s�lo en paquetes de energ�a. El fot�n se interpreta como un cuantum (cantidad m�nima indivisible) de campo electromagn�tico.