IV. ESPACIO Y TIEMPO

A quien no es matem�tico lo sobrecoge un misterioso escalofr�o cuando oye hablar de objetos "cuatridimensionales" como si se tratara de conceptos ocultos. Y, sin embargo hay afirmaci�n m�s trivial que decir que nuestro mundo es un espaciotiempo continuo cuatridimensional.

A. EINSTEIN

�

LA TEOR�A de la relatividad de Einstein alter� b�sicamente nuestros conceptos de espacio y tiempo, que dejaron de ser categor�as independientes para fusionarse en un solo concepto: el espaciotiempo.

El espacio posee tres dimensiones: esto quiere decir que, para determinar la posici�n de un punto, se necesita un sistema de referencia y tres n�meros (llamados coordenadas) (Figura 12). O, dicho de otro modo, que todo cuerpo posee altura, anchura y profundidad. El tiempo, por otro lado, es unidimensional y s�lo se necesita un n�mero para precisar un intervalo de tiempo. En la mec�nica cl�sica, el espacio y el tiempo eran dos absolutos, independientes entre s�. En la teor�a de la relatividad, se unen para formar el espaciotiempo de cuatro dimensiones: tres dimensiones espaciales y una dimensi�n temporal; cada "punto" del espaciotiempo es un suceso que se caracteriza con cuatro n�meros: tres para describir la posici�n donde ocurre y uno para determinar el tiempo al que sucede. El hecho de que el espaciotiempo tenga cuatro dimensiones no es nada sorprendente, al contrario de lo que podr�a sugerir la idea de una cuarta dimensi�n. Lo �nico novedoso es que las cuatro coordenadas del espaciotiempo aparecen unidas en la teor�a de la relatividad, mientras que en la f�sica cl�sica est�n disociadas en tres espaciales y una temporal.

Incluso, el espaciotiempo de cuatro dimensiones posee propiedades geom�tricas bien establecidas. Esto lo demostr� en forma convincente el matem�tico Herman Minkowski, poco despu�s de que apareciera la teor�a de la relatividad. Los fen�menos f�sicos ocurren en el espaciotiempo que los f�sicos y matem�ticos llaman espacio de Minkowski, un espacio de cuatro dimensiones en el que cada punto es un suceso y en el que se puede, incluso, definir la "distancia" entre sucesos.¹

LA CONTRACCI�N DEL TIEMPO

Evidentemente, la contracci�n relativista del tiempo es muy importante en el caso de las part�culas que se mueven a velocidades cercanas a la de la luz. Los f�sicos que estudian las part�culas elementales utilizan aceleradores de part�culas, que son aparatos que imprimen una velocidad, cercana a la de la luz, a electrones, protones o n�cleos at�micos. Estas part�culas, al chocar entre s�, se "rompen", o, m�s precisamente, producen nuevas part�culas al transformar su energ�a en masa. En este tipo de experimentos, el uso de la mec�nica relativista es tan com�n como lo es el uso de la mec�nica newtoniana a un ingeniero que construye edificios o puentes.

Tendremos oportunidad de regresar a las part�culas elementales en el cap�tulo IV. Por ahora, vamos a ofrecer al lector una aplicaci�n de la teor�a de la relatividad a un tema que, si bien no es de uso pr�ctico por ahora, podr� ser muy importante en el futuro y es bien conocido a trav�s de los libros y pel�culas de ciencia ficci�n: los viajes interestelares.

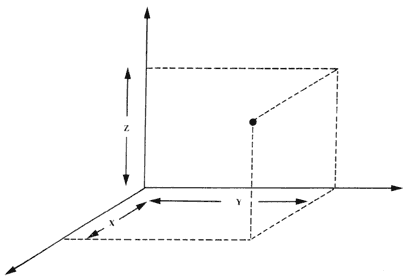
Figura 12. Un sistema de coordenadas permite localizar un punto en el espacio usando tres n�meros: x, y, z.

Supongamos que, alguna vez en el futuro, la humanidad llega a disponer de naves espaciales capaces de viajar a una velocidad cercana a la de la luz. Los dos sistemas de referencia a considerar son, entonces, la Tierra y la nave espacial. �C�mo se relacionan entre s� los tiempos medidos en esos dos sistemas? La f�rmula de la p�gina permite calcularlo. Hay que precisar que esta f�rmula es v�lida s�lo para un sistema de referencia inercial que se mueve a una velocidad constante con respecto a otro sistema; en el caso de movimientos m�s complicados, la f�rmula exacta ser�, en general, distinta. Por ahora consideraremos s�lo velocidades constantes por razones de simplicidad, aunque mencionaremos m�s adelante el caso de un movimiento m�s apropiado para un viaje interestelar.

Supongamos, por ejemplo, que una nave espacial viaja a la estrella m�s cercana, Alfa Centauri, que se encuentra a cuatro a�os luz de distancia. Al tratar distancias c�smicas utilizaremos el a�o luz como unidad de medida: es la distancia recorrida por la luz en un a�o y equivale a unos nueve billones de kil�metros. Los tripulantes de la nave no sentir�n nada en particular con respecto a su tiempo pues sus relojes marchar�n normalmente. Ser� a su regreso a la Tierra cuando notar�n que los relojes terrestres y los de la nave no coinciden: el tiempo medido en la nave, desde que sali� hasta que regres�, ser� un factor veces m�s corto que el mismo periodo de tiempo medido en la Tierra.

Algunos ejemplos cuantitativos ilustrar�n este efecto: Si la nave espacial viaja a una velocidad de "s�lo" 100 000 kil�metros por hora, por ejemplo, tardar� unos 80 000 a�os en llegar a Alfa Centauri y regresar a la Tierra: el tiempo transcurrido en la nave ser� s�lo unas tres horas m�s corto que el registrado en la Tierra. Pero si la velocidad de la nave espacial es cercana a la de la luz, la contracci�n del tiempo se manifestar� en toda su magnitud: si la nave viaja a 299 000 kil�metros por segundo, transcurrir�n poco m�s de ocho a�os, medidos en la Tierra, desde el momento en que despega la nave hasta que regresa, pero para los tripulantes habr�n pasado �solamente siete meses!; y si el viaje se realiza al centro de nuestra Galaxia; distante 30 000 a�os luz, a la misma velocidad de 299 000 kil�metros por segundo, entonces pasar�n 60 000 a�os en la Tierra, pero ese mismo viaje durar� s�lo 4 400 a�os para los tripulantes de la nave espacial; quiz�s puedan permanecer en hibernaci�n durante ese tiempo, pero cuando regresen, la Tierra ser� muy distinta a como la dejaron.

Los veh�culos espaciales lanzados en la actualidad est�n muy lejos de alcanzar velocidades cercanas a la luminosa. Para ellos, el efecto de la contracci�n del tiempo es extremadamente peque�o, pero no despreciable si se quieren realizar mediciones de muy alta precisi�n. Las variaciones relativistas del tiempo se toman en consideraci�n, como parte de la rutina para guiar los sat�lites artificiales y determinar su posici�n con gran exactitud.

La contracci�n del tiempo que ocurre en un viaje interestelar a gran velocidad parecer�a conducir, a primera vista, a una contradicci�n con el principio de la relatividad. En efecto, consideremos el caso de dos gemelos, uno de los cuales se queda en la Tierra y el otro realiza un viaje a las estrellas con una velocidad cercana a la de la luz. Como indicamos anteriormente, el gemelo viajero regresar� a la Tierra m�s joven que su hermano que se qued�. Pero, de acuerdo con el principio de relatividad, el tripulante de la nave espacial puede afirmar que �l est� en reposo y es la Tierra la que se mueve; ning�n experimento f�sico puede demostrarle lo contrario. Sin embargo, de acuerdo con esta interpretaci�n, el gemelo que permaneci� en la Tierra debe ser el m�s joven, cuando la Tierra se "vuelva a unir" con la nave espacial. �sta es la llamada Paradoja de los gemelos.

La situaci�n anterior se puede ver m�s claramente si suponemos que una c�mara y un receptor de televisi�n se encuentran en la nave espacial. �C�mo se ver�an mutuamente los que se quedan en la Tierra y los que viajan? Hay que tomar en cuenta que, adem�s de la contracci�n relativista del tiempo, tambi�n influye el hecho de que la distancia entre la Tierra y la nave aumenta gradualmente, por lo que las se�ales luminosas tardan cada vez m�s en llegar de un sistema al otro. Si se toman en cuenta estos dos efectos combinados —contracci�n del tiempo y retraso de la luz— resulta que el tiempo en un sistema se ve transcurrir m�s r�pidamente o m�s lentamente en otro sistema seg�n si ambos sistemas se acercan o se alejan. As�, mientras la nave espacial se aleja, veremos que los relojes, y todos los procesos f�sicos en �l, caminan m�s lentamente, como si estuvi�ramos observando el interior de la nave en c�mara lenta. Durante el recorrido de regreso, mientras la nave se acerca a la Tierra, suceder� lo contrario: el tiempo en la nave visto desde la Tierra, o viceversa, parecer� transcurrir m�s r�pidamente, y cada observador, en la Tierra y en la nave espacial, ver� al otro como en c�mara r�pida. Al llegar el veh�culo espacial a la Tierra, podr�n comparar sus calendarios y restar� que, de todos modos, el tiempo transcurrido en la nave es menor por un factor tal como indicamos m�s arriba. Por supuesto, la aparente contracci�n o dilataci�n del tiempo es un efecto notable s�lo para velocidades cercanas a la de la luz.

Hasta aqu� hemos considerado s�lo viajes interestelares a velocidad constante. En esa situaci�n, los pasajeros de una nave espacial no podr�an percatarse, mediante la observaci�n de efectos f�sicos, si se mueven o si se encuentran varados en el espacio: mientras la velocidad de la nave no cambie, sus pasajeros permanecer�n flotando ingr�vidamente en �l. Pero en un viaje m�s realista, la velocidad del veh�culo espacial debe empezar desde cero, acelerarse para aumentar progresivamente su velocidad y, en alg�n momento, empezar a frenarse para llegar a su destino con velocidad cero. Hay muchas maneras de lograr un viaje con estas caracter�sticas, pero el recorrido m�s sencillo es uno en el que la velocidad se aumenta uniformemente, es decir, se mantiene una aceleraci�n constante. En la f�sica cl�sica, un cuerpo que se acelera constantemente aumenta indefinidamente su velocidad; pero cuando la velocidad empieza a acercarse a la de la luz, surgen efectos relativistas que hay que tomar en cuenta: se puede demostrar que la velocidad del cuerpo se acerca gradualmente a la velocidad de la luz, pero sin alcanzarla nunca.

Para los tripulantes de un veh�culo espacial, lo m�s c�modo es que la aceleraci�n sea de unos 9.8 m/seg² (es decir, la velocidad aumenta 9.8 metros por segundo cada segundo), o sea; 1 g, la aceleraci�n con que los cuerpos caen en la superficie terrestre debido a la gravedad. De esa forma, los tripulantes se sentir�n en cada momento como si estuvieran en la Tierra, en lugar de flotar ingr�vidamente (recu�rdese que en un veh�culo que se acelera, aparece una fuerza inercial que atrae a los ocupantes hacia la parte trasera del veh�culo).

As�, un posible itinerario de viaje para ir de la Tierra a una estrella lejana podr�a ser el siguiente: la nave espacial se acelera uniformemente, aumentando cada vez m�s su velocidad hasta que, a la mitad del trayecto, el veh�culo rota 180 grados y, a partir de ese momento, los motores de la nave la desaceleran (en la segunda parte del trayecto, el techo y el piso del veh�culo espacial deben intercambiarse); finalmente, la nave llega a su destino con velocidad cero y sus tripulantes pueden aterrizar en alg�n planeta de la estrella a la que se dirigieron. El viaje de regreso es semejante: en la primera mitad del trayecto la nave se acelera y en la segunda mitad se desacelera, llegando a la Tierra con velocidad cero para poder aterrizar.

Veamos ahora cu�nto tarda un paseo como el descrito. A la aceleraci�n de 1 g, un viaje de ida y vuelta a Alfa Centauri, a cuatro a�os luz de distancia, tardar�a unos 11 a�os y cuatro meses para los que se quedan en la Tierra, pero s�lo siete a�os para los pasajeros de la nave espacial, debido a la contracci�n del tiempo. Si el viaje es m�s largo la diferencia de los tiempos es m�s notable: por ejemplo, al centro de nuestra galaxia, que se encuentra a 30 000 a�os luz, el viaje de ida y vuelta tardar�a 60 000 a�os medidos en la Tierra y s�lo 40 a�os para los viajeros c�smicos; la nave espacial alcanzar�a una velocidad m�xima que s�lo difiere una 2 000 millon�sima de la velocidad de la luz; sus tripulantes regresar�n cuando quiz�s ya no exista el g�nero humano. Para otras distancias, v�ase la tabla 1.

TABLA 1. Caracter�sticas de un vuelo interestelar que empieza desde el reposo, aumenta su velocidad con aceleraci�n 1 g, alcanza una velocidad m�xima V_max y se desacelera 1g hasta llegar con velocidad cero a una distancia D; t es el tiempo recorrido medio en la tierra y t es el tiempo transcurrido en la nave espacial. En los viajes de ida y vuelta, los tiempos simplemente se duplican.

D ( años luz )	V max / c	t ( años )	t ( años )
10	.986	11.8	4.9
100	.99981	101.9	9.2
1000	.999998	1002	13.7

 

En conclusi�n, parecer�a que los viajes interestelares son m�s factibles de realizarse gracias al efecto relativista de la contracci�n del tiempo. Desgraciadamente, el problema de la energ�a requerida para un viaje c�smico no es de f�cil soluci�n, como veremos en el cap�tulo siguiente. Pero sigamos por ahora sin preocuparnos por la energ�a y veamos si existe alguna una esperanza, de traspasar la velocidad de la luz.

�M�S R�PIDO QUE LA LUZ?

Hemos se�alado anteriormente que la velocidad de la luz es una barrera natural a la velocidad que puede adquirir cualquier cuerpo o se�al; la energ�a necesaria para alcanzar esa velocidad es infinita para una part�cula masiva, y s�lo una part�cula sin masa, como el fot�n, puede alcanzarla.

Para nuestras necesidades pr�cticas, la velocidad de la luz es un l�mite sumamente generoso. La luz tarda s�lo 0.13 segundos en dar una vuelta a la Tierra, por lo que la comunicaci�n terrestre no representa ning�n problema en cuanto a rapidez. Sin embargo, la limitaci�n impuesta por la velocidad de la luz empieza a manifestarse a escala c�smica. Por ejemplo, la luz tarda entre cuatro y 20 minutos en ir de la Tierra a Marte, dependiendo de las posiciones que estos planetas ocupen; hasta 50 minutos en llegar a J�piter y una hora y cuarto para alcanzar Saturno. Por esta raz�n, los veh�culos espaciales lanzados a explorar los planetas exteriores del Sistema Solar no pueden teledirigirse instant�neamente desde la Tierra, lo cual dificulta considerablemente su manejo. Y, cuando se env�e una misi�n tripulada a Marte, la comunicaci�n con los tripulantes no podr� ser directa, sino con retrasos de varios minutos entre recepci�n y emisi�n de mensajes. La situaci�n es a�n peor para las comunicaciones con las estrellas; nuestra vecina m�s cercana, Alfa Centauri, se encuentra a cuatro a�os luz de distancia por lo que un mensaje enviado a una supuesta civilizaci�n alrededor de esa estrella tardar�a al menos ocho a�os en ser contestado. El tama�o de nuestra Galaxia es de cien mil a�os luz, de modo que una vida humana no puede bastar para conversar con civilizaciones extraterrestres.

En cuanto a viajar a estrellas lejanas, la contracci�n relativista del tiempo puede beneficiar a los tripulantes de la nave espacial, acortando el tiempo de un trayecto; pero el transcurrido en la Tierra puede ser de siglos o milenios.

Por todo lo anterior, la imposibilidad de rebasar la velocidad de la luz parece que nos condena a permanecer eternamente en nuestro peque�o rinc�n de la Galaxia, separados por enormes distancias de otros astros —salvo unos cuantos muy cercanos— y, quiz�s, de civilizaciones extraterrestres. Por eso, la posibilidad de viajar, o al menos comunicarse, a una velocidad superior a la luz es una ilusi�n muy cara; sin embargo, las dificultades no son simplemente t�cnicas, sino que est�n relacionadas con la misma geometr�a del espaciotiempo.

En primer lugar, si bien es cierto que se necesita una energ�a infinita para alcanzar la velocidad de la luz, cabe preguntarse si no existe alg�n mecanismo desconocido, quiz�s relacionado con efectos cu�nticos, que permita rebasar esa barrera en alguna forma no prevista por la f�sica actual. Adem�s podr�an existir part�culas que, desde que naci� el Universo, posean una velocidad superior a la luminosa; a tales hipot�ticas part�culas incluso se les ha dado un nombre: taquiones (del griego tachys: velocidad). Si existieran, los taquiones resolver�an el problema de las comunicaciones interestelares, al permitir enviar mensajes m�s veloces que las se�ales luminosas. Por otra parte, en algunos libros o pel�culas de ciencia ficci�n los personajes se "teletransportan", o viajan a trav�s de un supuesto "hiperespacio", o cualquier cosa que implique su desaparici�n en un punto y su aparici�n en otro muy lejano. Pero veremos a continuaci�n que la posibilidad de viajar o enviar se�ales m�s r�pidamente que la luz equivale a un viaje aparentemente muy distinto, pero m�s dif�cil de concebir: �un viaje al pasado!

El tiempo transcurrido entre dos sucesos depende de la velocidad de quien lo mide. Supongamos que en alg�n lugar se produce el suceso A, consistente en la emisi�n de una part�cula material, o de una se�al luminosa; tal part�cula o se�al es recibida en otro punto en alg�n momento: llamemos suceso B a esa recepci�n distante. El tiempo transcurrido entre los sucesos A y B depende del sistema de referencia en el que se observan esos dos sucesos y var�a, por lo tanto, de acuerdo con la velocidad del observador. Sin embargo, se puede denostar que, debido a la estructura geom�trica del espaciotiempo, el tiempo transcurrido entre A y B no puede nunca invertirse: no existe ning�n observador para quien la recepci�n de la se�al (suceso B) preceda su emisi�n (suceso B). �ste es, el principio de causalidad, fundamental en la f�sica: si el suceso A es la causa de suceso B, entonces A sucede antes que B en cualquier sistema de referencia: el orden causa-efecto es invariante.

Sin embargo, para que los dos sucesos considerados tengan una relaci�n causal, es decir que A pueda influir sobre B, es necesario que la acci�n de A viaje a una velocidad menor o igual que la velocidad de la luz.

Por ejemplo, lo que ocurre en la Tierra a la 1 P.M. puede ser un suceso conectado causalmente con el suceso que ocurre en la Luna a las 2 P.M. ya que una hora es suficiente para ir o mandar una se�al a la Luna, incluso a velocidades menores a la de la luz. Por otra parte, lo que sucede en este instante en la estrella Alfa Centauri no puede tener relaci�n causal con ning�n suceso presente en la Tierra; si Alfa Centauri explotara en este momento, tendr�amos que esperar al menos cuatro a�os para enterarnos de ello.

Ahora bien, el principio de causalidad no se aplica a las part�culas que se mueven m�s r�pidamente que la luz. Si el suceso A es la emisi�n de un taqui�n y el suceso B la recepci�n de ese taqui�n, entonces puede existir un sistema de referencia en el cual B antecede a A , es decir, el receptor parece emitir al taqui�n y el emisor recibirlo: se puede demostrar que eso ocurre en cualquier sistema de referencia que se mueva con respecto al emisor y al detector con una velocidad superior a c²/v_T, donde v_T es la velocidad del taqui�n (la velocidad del sistema de referencia mencionado es menor que c porque v_T es mayor que c). Dicho de otro modo, el concepto de pasado y futuro para un taqui�n es relativo. Un taqui�n "viaja" hacia el futuro o hacia el pasado, seg�n la velocidad de quien lo observa.

As�, de existir los taquiones, o cualquier posibilidad de desplazarse m�s r�pidamente que la luz, ser�a posible, viajar al pasado. Por ejemplo, se podr�a utilizar un dispositivo consistente en dos emisores-receptores de taquiones que se alejan uno de otro a velocidad lo suficientemente grande. El primer aparato emite una se�al taqui�nica, que el segundo aparato recibe y contesta inmediatamente con otra emisi�n de taquiones. �La respuesta llegar�a al primer aparato antes de que haya emitido su primera se�al! (Figura 13.)

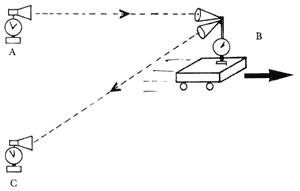
Figura 13. Un sistema de emisores y detectores de taquiones podr�a permitir que una se�al taqui�nica regrese antes de salir.

O bien, imagin�monos que en el futuro se inventara un "teletransportador" tal que permitiera a un viajero espacial desaparecer en la Tierra y materializarse en alg�n lugar lejano, implicando un desplazamiento a mayor velocidad que la luz. Nuestro viajero podr�a llevarse un teletransportador consigo para poder regresar a la Tierra. Pero, en ese caso, cabe la posibilidad de que el viajero inicie su retorno desde un planeta en movimiento tal que �regrese antes de haber salido!

�Es posible viajar al pasado? Independientemente de cualquier restricci�n impuesta por las leyes de la f�sica, el hecho de regresar en el tiempo implica una situaci�n sumamente contradictoria. En efecto, si una se�al taqui�nica puede regresar antes de ser emitida, �qu� pasar�a si en el lapso de tiempo entre su recepci�n y su misi�n se decide destruir el emisor de taquiones? M�s a�n, si una persona pudiera regresar al pasado �qu� ocurrir�a si se encontrara consigo mismo de ni�o... y decidiera "asesinarse" ?

Invertir el sentido del tiempo no parece ser factible, m�s por razones l�gicas que por motivos f�sicos. Lo que, no es tan evidente, y queremos subrayarlo, es que, debido a la peculiar geometr�a del espacio tiempo, un viaje en el espacio a mayor velocidad que la luz es enteramente equivalente a un viaje hacia atr�s en el tiempo, con todo y sus contradicciones inherentes. Al parecer, estamos efectivamente condenados a vivir en una peque�a regi�n perif�rica de nuestra Galaxia, y s�lo contemplar la inmensidad del Universo a trav�s de la luz que las galaxias lejanas nos enviaron hace millones de a�os.

LA APARIENCIA �PTICA DE LOS CUERPOS EN MOVIMIENTO

De acuerdo con la teor�a de la relatividad, se podr�a pensar que un cuerpo en movimiento sufre una contracci�n; sin embargo, ha habido mucha confusi�n sobre este efecto. En primer lugar, no se trata de una contracci�n real, en el sentido de que un cuerpo que se mueve se comprime realmente. M�s bien, se trata de c�mo se percibe el tama�o de un cuerpo en un sistema de referencia en el que �ste aparece en movimiento.

Medir la longitud de una barra equivale a medir la distancia entre sus dos extremos. Es evidente que si la barra se mueve, la posici�n de sus dos extremos debe determinarse simult�neamente para que la medici�n tenga sentido (obviamente no se puede medir el largo de un coche en movimiento marcando en el suelo la posici�n de su parte delantera primero, y m�s tarde la posici�n de su parte trasera). Lo anterior es trivial en mec�nica cl�sica, pues no hay ambig�edad sobre la medici�n del tiempo, pero la situaci�n se complica si la velocidad de la barra es suficientemente alta para que aparezcan los efectos relativistas. Si en un sistema de referencia determinamos la posici�n de los dos extremos de la barra al mismo tiempo, ese mismo par de mediciones no habr�n ocurrido simult�neamente en otro sistema de referencia que se mueve con respecto al primero.

En la teor�a de la relatividad, la simultaneidad es un concepto relativo. Dos sucesos que ocurren a la misma hora para un observador, pueden ocurrir a horas distintas para otro. Por lo tanto, si insistimos en definir la longitud de una barra como la distancia entre sus dos extremos, medida simult�neamente, esa longitud debe ser distinta para quien ve la barra en movimiento. Se puede demostrar que el efecto neto es una reducci�n de la longitud de la barra por un factor con respecto a la longitud de la barra en reposo. Debemos insistir, sin embargo, en que esta contracci�n se debe m�s bien a la definici�n misma de longitud y a la relatividad del tiempo, y no a la contracci�n real, en la que los �tomos de la barra se comprimen. La supuesta contracci�n de los cuerpos en movimiento ha sido fuente de muchas confusiones y es el tema favorito de los aficionados a la f�sica que intentan refutar la teor�a de la relatividad busc�ndole contradicciones.

Es curioso que pasaran varias d�cadas, desde la aparici�n de la teor�a de la relatividad, para que se planteara un problema relativamente simple: �c�mo se ven los cuerpos que se mueven a velocidades muy altas? La apariencia �ptica de un cuerpo en movimiento, es decir lo que se observa directamente, no debe confundirse con la contracci�n mencionada m�s arriba. Incluso si no se toman en cuenta efectos relativistas de contracci�n del tiempo, un cuerpo que se mueve con una velocidad comparable con la de la luz debe verse deformado. Esto se debe a que la luz recibida simult�neamente de un objeto en movimiento no parti� simult�neamente de todas sus partes. Si, por ejemplo, el cuerpo se aleja, la luz necesita un poco m�s de tiempo para viajar del extremo delantero al observador que del extremo trasero; en consecuencia, como puede verse en la figura 14, el cuerpo se ve m�s corto de lo que es realmente. Del mismo modo, un cuerpo que se acerca se ve m�s largo de lo que es en realidad.

El efecto anterior debe combinarse con la contracci�n relativista del tiempo para deducir qu� apariencia tiene un cuerpo cuya velocidad es cercana a la luminosa. El resultado es muy curioso, aunque de poca relevancia pr�ctica. Se puede demostrar, por ejemplo, que una esfera en movimiento sigue vi�ndose como esfera, pero una barra recta aparece doblada. Tambi�n se ha demostrado que un objeto lejano (cuyo tama�o aparente es peque�o) no se ve deformado ni contra�do: por ejemplo, un cubo en movimiento sigue vi�ndose como cubo, pero rotado.

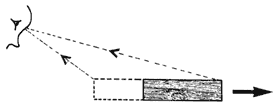
Figura 14. La apariencia �ptica de un cuerpo en movimiento se ve afectada por el tiempo desigual que tarda la luz en llegar de diferentes partes.

Figura 15. Apariencia del cielo estrellado desde una nave espacial.

Otro efecto curioso (y que no ha sido aprovechado en las pel�culas de ciencia ficci�n) es la apariencia del cielo estrellado desde una nave espacial que viaja a una velocidad cercana a la de la luz. La posici�n aparente de las estrellas cambia como si estuvieran atra�das por el punto en el cielo hacia donde se dirige la nave: las estrellas se ven concentradas alrededor de ese punto, mientras que desde la parte trasera de la nave se observa un cielo despoblado (Figura 15). Por supuesto, el efecto es tanto m�s pronunciado como mayor la velocidad del veh�culo espacial.