I. FUNDAMENTOS DE LA ELECTRICIDAD
ESTE cap�tulo introductorio trata de los principios y definiciones del paso de un flujo el�ctrico a trav�s de un circuito. En cap�tulos posteriores aplicaremos estos conocimientos fundamentales al an�lisis de un circuito de protecci�n cat�dica para determinar los indicadores de la eficiencia de un proceso, como el voltaje de celda, las ca�das �hmicas en diversas partes del circuito, la distribuci�n de corriente, etc�tera.
Para describir un circuito el�ctrico simple estudiaremos un sistema de protecci�n cat�dica el cual puede consistir simplemente en una fuente de poder conectada a uno o m�s componentes, principalmente resistores (ser�n descritos m�s adelante), por medio de un alambre hecho de un material conductor (cobre, por ejemplo), el circuito el�ctrico simple constituye una fuente de poder que va a proporcionar una fuerza electromotriz estableciendo diferencias de potencial a trav�s de los varios componentes del circuito e impulsando la corriente a trav�s de ellos. Todos estos componentes ofrecer�n varios grados de resistencia al flujo de la corriente.
En cualquier circuito el�ctrico, entonces, existen varios fen�menos que tenemos que medir:
1) La corriente, medida en amperes (A);
2) La fuerza electromotriz y la diferencia de potencial, ambas medidas en voltios (V);
3) La resistencia, medida en ohms (W).
La naturaleza y los tipos de materiales que participan en las reacciones electroqu�micas de un sistema de protecci�n cat�dica pueden tener un gran efecto sobre los resultados que se obtengan. Es, por lo tanto, necesario familiarizarse con los factores que influyen en la conducci�n de corriente.
La conductividad el�ctrica es el movimiento de la carga el�ctrica. La habilidad de diferentes substancias para permitir el flujo de una carga est� determinada por la movilidad de los electrones portadores de la carga o de los iones que contenga la sustancia.
Los conductores de primer orden son aquellos que poseen conductancia el�ctrica, en los cuales los portadores de la carga son los electrones. Se caracterizan por tener una conducci�n sin transferencia substancial de masa. La mayor�a de los metales, el grafito y algunos �xidos muestran este tipo de conducci�n. A veces, a estos materiales se les conoce como conductores met�licos y su conductividad decrece cuando aumenta la temperatura.
Los conductores de segundo orden poseen conductancia i�nica o electrol�tica, y los portadores de la carga son los iones. En este tipo de conductores se da una transferencia de masa asociada con la conductividad. Las soluciones acuosas con sales disueltas, los suelos y las sales i�nicas son algunos ejemplos de este tipo de conductores. Su conductividad aumenta cuando se incrementa la temperatura.
Conductores mixtos o de tercer orden
Algunos materiales, llamados com�nmente semiconductores, poseen tanto conductancia i�nica como el�ctrica. Por lo general predomina el car�cter el�ctrico. Su conductividad es demasiado baja en general, pero aumenta r�pidamente con la temperatura. La mayor�a de los �xidos met�licos (NiO, ZnO, etc.) y algunos metales (Si, Ge, etc.) se agrupan dentro de esta categor�a.
Otras clases de materiales que merecen ser mencionados son los aislantes. La conductancia en ellos es muy dif�cil, sin importar el tipo de mecanismo que participe en la conductividad, sobre todo si se les compara con la de los conductores mencionados antes.
La influencia del proceso de conducci�n en la conducta electroqu�mica de las reacciones es muy importante Cada reacci�n de corrosi�n, as� como las presentes en sistemas de protecci�n cat�dica, tienen un origen electroqu�mico y se presentan en la interfase entre un conductor de primer orden (el�ctrico) y uno de segundo orden (electrol�tico). Por ejemplo, si un metal (conductor) tiene una pel�cula de �xido o una capa de pintura (aislantes) sobre su superficie, se estar�a esperando con esto que tuviera una alta resistencia en la transferencia de electrones. Esto cambiar�a la velocidad de la reacci�n y la energ�a requerida para llevarla a cabo.
Ya que un electr�n es una unidad de carga muy peque�a, para medirlo se utiliza una unidad m�s grande denominada coulomb. Un coulomb corresponde a 6.24 trillones de electrones (6.24 x1012). A la velocidad de flujo de la carga el�ctrica se le conoce como corriente el�ctrica (intensidad [I]). En fen�menos el�ctricos la carga es an�loga al volumen de l�quido (litros) que fluye por una tuber�a y la corriente es equiparable a la velocidad de flujo (cantidad de litros por minuto) en dicha tuber�a.
El flujo de la carga puede trasladarse por medio de electrones (corriente el�ctrica) o por iones (corriente i�nica). El flujo de corriente en metales se da a trav�s de un flujo de electrones. Un electrolito es aquella sustancia que conduce corriente por flujo i�nico.
La unidad b�sica de la corriente el�ctrica (I) es el ampere (A). Un ampere se define como la velocidad de flujo de una carga (Q) de un coulomb, por segundo. As� se expresa esta unidad para el consumo de algunos equipos el�ctricos grandes o de celdas electrol�ticas industriales a diferencia de los circuitos electr�nicos transistorizados o las t�cnicas electroqu�micas, en los cuales se emplean com�nmente dos subm�ltiplos de esta unidad que son el miliampere (mA: 0.001 A) y el microampere (mA: 0.000001 A).
Resumiendo, podemos decir que:
De lo anterior se deduce que la cantidad total de electricidad (Q), en coulombs, que pasa por cualquier punto de un circuito el�ctrico es el producto de la corriente (I), en amperes, y el tiempo (t) en segundos:
UNIDAD DE DIFERENCIA DE POTENCIAL. EL VOLT
Cuando una corriente el�ctrica fluye a trav�s de un alambre conductor, se dice
que lo hace porque existe una diferencia de potencial entre los dos extremos
del alambre. La diferencia de potencial entre dos puntos se define como el trabajo
efectuado (que se mide en joules), cuando un coulomb de electricidad se mueve
de un punto al otro. A la unidad con que se mide la diferencia de potencial
se le llama volt y se define como sigue: dos puntos tienen una diferencia de
potencial de 1 volt cuando se realiza un trabajo de 1 joule por cada coulomb
de electricidad que transita de un punto al otro; por lo tanto
La fuerza electromotriz (fem) de una celda se mide en volts y se define como la suma de las diferencias de potencial que puede producir a trav�s de todos los componentes de un circuito al cual est� conectado, incluyendo la diferencia de potencial requerida para impulsar la corriente a trav�s de la misma celda.
La fem de una celda en volts se define entonces como el trabajo total efectuado en joules por los coulombs de electricidad transportados en un circuito en el que la celda est� conectada.
Se ha dicho que los diferentes materiales pueden ser clasificados como conductores buenos o malos y como aislantes. En lo que se refiere a la corriente el�ctrica, por lo general se piensa en t�rminos de la habilidad de una sustancia para oponerse al flujo de corriente que pasa por ella. Un buen conductor, se dice, tiene una resistencia peque�a y un mal conductor, una resistencia alta.
Se ver� m�s adelante que la resistencia de un material depende de sus dimensiones y de la sustancia con que est� hecho. Para un cable de dimensiones dadas, la plata ofrece la menor resistencia al paso de la corriente, pero como este metal es demasiado caro para un uso com�n, se usa el cobre para el cableado y la conexi�n de alambres en los circuitos el�ctricos.
Cuando se requiere de una alta resistencia, se emplean casi siempre ciertas
aleaciones especiales, para reducir la corriente en un circuito, como el constantan,
el manganin y el nicromel.1![[Nota 1]](../imgs/mcommnt.gif){kind=small}
El constantan se emplea para uso general, mientras que el manganin se emplea m�s bien para manufacturar resistores estandarizados de alta calidad, ya que estas aleaciones presentan peque�os cambios en la resistencia debidos a la temperatura.
En 1826 el profesor de f�sica Simon Ohm estableci� la siguiente ley como resultado
de varios experimentos que efectu� para investigar la relaci�n entre la corriente
que pasa por un alambre y la diferencia de potencial establecida entre los extremos
del mismo: "La corriente que pasa por un alambre a temperatura constante es
proporcional a la diferencia de potencial en sus extremos." El conductor que
siga esta relaci�n (los conductores el�ctricos) obedece a la ley de Ohm:
El valor de la constante en la ecuaci�n anterior (que es alto cuando el valor de la corriente es peque�o y bajo cuando la corriente es grande) puede ser usado como una medida de la resistencia del alambre:
|
diferencia de potencial
|
= resistencia |
|
|
|
|
corriente
|
En otras palabras, la resistencia de un conductor es la proporci�n de la diferencia de potencial a trav�s de �l y la corriente que fluye. A la unidad de resistencia el�ctrica se le llama ohm y se define como: "la resistencia de un conductor dado, cuando se aplica una diferencia de potencial de 1 volt en sus extremos y una corriente de 1 ampere fluye por �l":
|
voltios
|
= ohms |
|
|
|
|
amperes
|
lo que formalizado de otra manera es:
La resistencia de un metal puro aumenta con la temperatura, pero la resistencia de otros materiales conductores, como el carb�n por ejemplo, decrece con la temperatura. En otras sustancias, como los semiconductores (germanio, silicio y selenio), las disoluciones i�nicas que contienen las sales y los suelos, la resistencia tambi�n disminuye cuando aumenta la temperatura.
Se dice que un n�mero de resistores, (R1, R2, R3, Rn, .....) est�n conectados en serie si su conexi�n es consecutiva extremo con extremo, de tal suerte que la misma corriente (I), en amperes, fluya a trav�s de cada una (Figura 1).
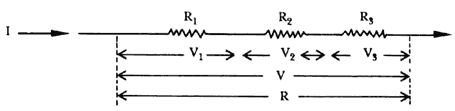
Figura 1. Parte de un circuito el�ctrico.
Si R es la resistencia combinada y V, en volts, es la diferencia
de potencial total a trav�s de los resistores:
pero como V es igual a la suma de las diferencias de potencial individuales a trav�s de R1, R2 y R3:
| V = V1 + V2 + V3 |
| V = 1R1 + 1R2 + 1R3 |
y dividiendo todo entre I, tenemos que:
Se dice que los resistores est�n en paralelo cuando son colocados uno al lado del otro y sus extremos permanecen unidos (Figura 2). La misma diferencia de potencial ser� entonces aplicada a cada uno, pero compartir�n la corriente en el circuito.
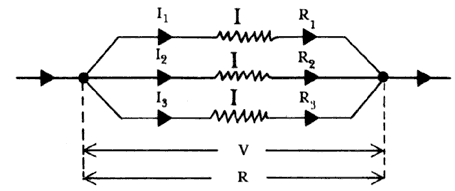
Figura 2. Parte de un circuito el�ctrico
Supondremos que la corriente (I) se divide en I 1I 2 e I 3 al pasar por R1, R2 y R3, respectivamente, y que la diferencia de potencial com�n es V.
Si R es la resistencia combinada, se puede reescribir:
|
I =
|
V
|
|
|
|
|
R
|
la corriente total es:
I = I 1+ I 2 + I 3
|
I =
|
V
|
+
|
V
|
+
|
V
|
|
|
|
|
|
||||
|
R1
|
R2
|
R3
|
||||
|
V
|
=
|
V
|
+
|
V
|
+
|
V
|
|
|
|
|
|
|
||||
|
R
|
R1
|
R2
|
R3
|
||||
y dividiendo todo entre V, tenemos que:
|
1
|
=
|
1
|
+
|
1
|
+
|
1
|
|
|
|
|
|
|
||||
|
R
|
R1
|
R2
|
R3
|
||||
IMPORTANCIA PRACTICA DE LA RESISTENCIA INTERNA DE UNA CELDA
Existen diversos tipos de celdas como, por ejemplo, las pilas secas, que pueden obtenerse de tama�os diferentes. Las fuerzas electromotrices de estas celdas ser�n id�nticas en tanto estas �ltimas sean fabricadas con el mismo material exactamente y con concentraciones de electrolitos iguales. La fuerza de la corriente que se obtiene de una celda no s�lo depende de su fuerza electromotriz, sino tambi�n de la resistencia interna propia. Con el fin de obtener una corriente grande, la resistencia interna debe de ser baja. En el caso de un acumulador, esto significa que las placas de plomo deben de tener una gran �rea y deben estar espaciadas a muy corta distancia. Asimismo, la concentraci�n del electrolito debe ser tal que su resistencia sea la m�s baja posible.
De acuerdo con su tama�o y construcci�n, la resistencia interna de una pila seca var�a de 0.5 a 1.0 ohm, y la fem es aproximadamente de 1.5 V. Por lo tanto, si las terminales de una pila seca son cortocircuiteadas con un pedazo grueso de alambre de cobre cuya resistencia sea despreciable, la m�xima corriente que se obtiene ser�a de 3 a 0.5 A.
La marcha el�ctrica de un motor de autom�vil necesita de una corriente alta para poder operar. Por esto, las bater�as o acumuladores de coches de combusti�n interna son fabricadas de celdas que contienen muchas placas delgadas con peque�os espaciamientos entre ellas. Ocho pilas secas en serie tendr�n la misma fem que la bater�a de 12 V de un coche, pero ser�an inoperativas para arrancar la marcha en virtud de su alta resistencia interna.
Se denomina bater�a a un grupo de celdas conectadas entre s�. Normalmente las
celdas se conectan en serie, o sea que el polo positivo de una es conectado
al extremo negativo de la pr�xima celda, etc. (v�ase la figura 3). En ocasiones,
sin embargo, pueden ser conectadas en paralelo, es decir, todos los extremos
positivos conectados entre s�, lo mismo que los extremos negativos (Figura 4).
|
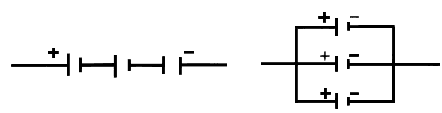
Figura 3. Celdas en serie. |
Figura 4. Celdas en paralelo. |
Cuando se requiere de la corriente m�xima de un n�mero dado de celdas, el arreglo empleado depender� de la resistencia del circuito externo. Hablando de manera general, se usa una conexi�n en serie cuando la resistencia del circuito es alta, comparada con la de las celdas, y se emplea una en paralelo cuando la resistencia es baja.
Cuando las celdas est�n conectadas en serie, la fem total de la bater�a es igual a la suma de las fems por separado y la resistencia interna es igual a la suma de las resistencias internas de las celdas por separado. Cuando celdas de igual fem y resistencia son conectadas en paralelo, la fem que resulta es la misma que la de una sola celda y la resistencia interna de la bater�a se calcular�a de acuerdo con la f�rmula de los resistores en paralelo.
Una ventaja que se obtiene al conectar celdas en paralelo es que existe un drenaje menor de corriente en las celdas, ya que �stas comparten la corriente total, mientras que en las conexiones en serie la misma corriente principal es proporcionada por cada una de las celdas.
Las celdas nunca se deben dejar conectadas en paralelo cuando no est�n en uso, ya que si la fem de una es ligeramente mayor que la de la otra, comenzar� a circular corriente en la bater�a misma y las celdas se agotar�n r�pidamente. Esto no sucede cuando se conectan en serie.
"P�RDIDA O CA�DA DE VOLTAJE" CUANDO UNA CELDA PRODUCE CORRIENTE EN UN CIRCUITO
Por razones pr�cticas, la fem de una celda puede medirse con un valor muy aproximado si tomamos la lectura de un volt�metro de alta resistencia conectado directamente a trav�s de las terminales de la celda cuando �sta no se encuentre conectada a ning�n circuito.
Supongamos que un volt�metro conectado a las terminales de una pila seca, con una resistencia interna de 2W , da una lectura de 1.5 V: Esta es la fem de la pila (Figura 5 a).
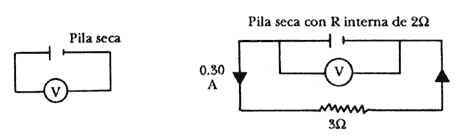
Figura 5. (a) El volt�metro de alta resistencia mide una fem de 1.5 V (se desprecia el flujo de corriente). (b) El volt�metro mide s�lo 0.90 V. Una p�rdida de voltaje de 0.60 V impulsa la corriente a trav�s de la resistencia interna.
Cuando un resistor de 3W se conecta a las terminales de la celda y una corriente fluye a trav�s de �l, se observa que la lectura del volt�metro ha ca�do a 0.90 V (Figura 5 b). La celda parece haber "perdido" 0.6 V (1.5 - 0.9 = 0.6 V). Esto puede explicarse como sigue: la corriente que circula por el circuito est� dada por
|
I=
|
fem
|
E
|
|
|
|
|
||
|
resistencia total
|
=
|
R+B
|
R = resistencia del circuito externo
B = resistencia interna de la celda.
|
I=
|
1.5
|
0.30 A.
|
|
|
|
=
|
||
|
3 + 2
|
|
La diferencia de potencial (dp) requerida para impulsar esta corriente a trav�s de la resistencia externa de 3 W es:
que es el valor de la lectura del volt�metro.
El volt�metro est� conectado a las terminales de la celda, pero en cambio si estuviera conectado a trav�s de los extremos de la resistencia de 3W , no habr�a diferencia alguna en la lectura. Esto se debe al hecho de que los alambres que conectan la celda a la resistencia tienen una resistencia despreciable y por consiguiente su dp tambi�n es despreciable; por lo tanto, la dp en las terminales de la celda es igual a la dp en el resistor.
La dp requerida para impulsar la corriente a trav�s de la misma celda est� dada por:
Corriente multiplicada por = 0.30 x 2.0 = 0.60 V, la resistencia interna
valor igual al "voltaje perdido" o sea la "ca�da de potencial" de la celda.
Se dijo al principio de esta secci�n que un volt�metro dar�a un valor muy aproximado de la fem de la celda. Esto se debe a que incluso un volt�metro de muy alta resistencia drena algo de corriente y por esta raz�n una peque�a parte de la fem de la celda se "perder�" en impulsar dicha corriente a trav�s del equipo de medici�n. Sin embargo, si la resistencia del volt�metro es muy alta, comparada con la resistencia de la celda, la corriente drenada ser� muy peque�a y en consecuencia la "ca�da de potencial" en este caso ser� num�ricamente despreciable.
Un ejemplo ilustrar� mejor lo expuesto l�neas atr�s: Dos estructuras met�licas enterradas, A y B, se encuentran conectadas el�ctricamente en paralelo a una bater�a de 12 V, cuya resistencia interna total es de 0.6 W , tal y como se representa en la figura 6. Las resistencias del terreno para A y B son de 4 y 6 W, respectivamente, y la resistencia total del cable es de 1W . Se trata entonces de encontrar la corriente que fluye a trav�s del suelo entre A y B. En la figura 6 simplificada, se supone que cualquier otra ca�da de potencial se ignorar� por el momento.
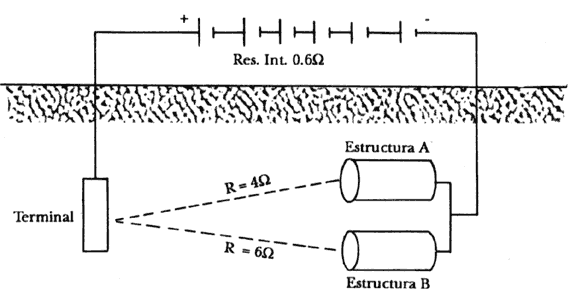
Figura 6. Estructuras met�licas enterradas, conectadas el�ctricamente a una bater�a.
El primer paso para estudiar un problema el�ctrico es dibujar un diagrama del circuito:
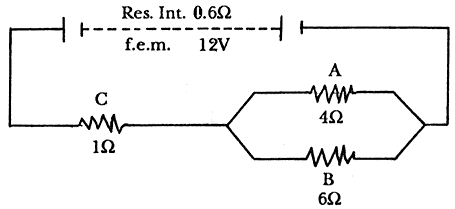
La resistencia combinada (R), en ohms, de A y B est� dada por:
|
1
|
=
|
1
|
+
|
1
|
+
|
6+4
|
R = 2.4
|
|
|
|
|
|
||||
|
R
|
4
|
6
|
24
|
por tanto, la resistencia total del circuito es:
|
corriente principal =
|
fem
|
12 | ||
|
|
=
|
|
=3A. | |
|
resistencia total
|
4 |
La dp a trav�s de A y B (la corriente multiplicada por la resistencia combinada) es igual, entonces, a:
Por lo tanto, la corriente a trav�s de A es igual a:
|
dp
|
7.2
|
= 1.8A,
|
|
|
|
=
|
|
|
|
resistencia
|
4
|
y la corriente a trav�s de B resultar� como sigue:
Cuando se fabrica un resistor, se emplea alambre grueso y corto si se quieren obtener bajas resistencias y, al rev�s, alambre delgado y largo si se desean resistencias altas. Adem�s de la longitud y del espesor, existe otro factor importante que se debe tomar en cuenta cuando se toma la decisi�n de seleccionar la longitud y el calibre de alambre para una resistencia en particular: el material del que est� hecho el alambre.
Supongamos, por ejemplo, que la longitud de un alambre es duplicada, lo que
duplica a su vez la resistencia, puesto que ahora la longitud del alambre equivale
a dos resistencias iguales en serie. Si la longitud del alambre es aumentada
cinco veces, la resistencia aumentar� de igual manera su valor previo cinco
veces. Las resistencia de un alambre por lo tanto es directamente proporcional
a su longitud, situaci�n que formalizamos as�:
Con respecto al espesor o �rea de secci�n transversal del alambre, los alambres gruesos pueden ser considerados como equivalentes a un n�mero de alambres delgados de �rea transversal igual, que se encuentren unidos en paralelo. Al duplicarse el �rea, la resistencia del alambre disminuir� por tanto a la mitad. En otras palabras, la resistencia de un alambre es inversamente proporcional al �rea de su secci�n transversal (A):
|
1
|
||
|
R a
|
|
;
|
|
A
|
si combinamos estos dos �ltimos resultados, tenemos:
|
1
|
||
|
R a
|
|
|
|
A
|
Esta relaci�n puede convertirse en una ecuaci�n que introduzca una constante, de la siguiente manera:
|
p1
|
||
|
R =
|
|
,
|
|
A
|
en donde p es una constante llamada resistividad del material
del alambre. Si en esta ecuaci�n damos a 1 un valor de 1 cm y
A vale 1cm2, tenemos:
|
1 cm
|
r
|
|||
|
R = r
x
|
|
=
|
|
,
|
|
1 cm2
|
1 cm
|
Con esta f�rmula, vemos que la resistividad de un material es expresada en una unidad ohm cent�metro y es num�ricamente igual a la resistencia de un conductor hecho de material con una longitud de 1 cm y de secci�n transversal de 1 cm2.
Se puede decir tambi�n que la resistividad es una constante del material, lo cual es independiente de la forma geom�trica del resistor. Por ejemplo, la resistencia que presenta un suelo al paso de la corriente el�ctrica es una variable que depende, como dijimos anteriormente, de la longitud y del �rea transversal al flujo de corriente. Sin embargo, la resistividad de ese suelo tiene un valor fijo, e independiente del flujo de corriente, del �rea transversal y de la longitud del terreno. Su valor s�lo variar� con la temperatura, el contenido de humedad, el de acidez y otros factores.
Lo contrario a la resistividad es la conductividad. Un material con alta conductividad tiene baja resistividad y viceversa. De esta manera se tiene que la resistencia al flujo de corriente es m�nima cuando:
a) el medio presenta baja resistividad (alta conductividad),
b) existe una distancia peque�a para el flujo de corriente, y
c) tenemos un �rea transversal grande para el flujo de corriente.
En cambio, la resistencia al flujo de corriente es m�xima cuando:
a) el medio presenta alta resistividad (baja conductividad),
b) las distancias son grandes para el flujo de corriente, y
c) el �rea transversal es peque�a para el flujo de corriente.
Las resistividades del suelo a menudo son mayores de 10 000 W-
cm. Las resistencias al flujo de corriente en sistemas de protecci�n cat�dica
en estos suelos pueden tener a veces valores menores a 1 ohm. La resistencia
puede ser baja en un medio con una alta resistividad si el �rea transversal
al flujo de corriente es grande.
|
|
|
|
Material
|
Resistividad (W-cm)
|
|
|
|
| Aluminio | 0.000003 |
| Latón | 0.000008 |
| Hierro | 0.000010 |
| Plomo | 0.000022 |
| Mercurio | 0.000094 |
| Suelo típico | 10 000 |
| Vidrio | 100 000 000 000 |
| Agua de mar típica | 30.00 |
|
|
|
|
|
|
Ampere × segundo = coulomb Volt × coulomb = joule Volt × ampere = watt Watt × segundo = joule KW = Kilowatt = 1.341 HP KWh = kilowatt = 1 000 watt / hora = 3 600 000 joules HP = caballo de vapor = 746 watt = 0.746 KW 1 joule = 0.2387 calorías / gramo (cal) 1 cal = 4.183 joules 1 HPh = 1 caballo de vapor / hora = 641.7 kilocalorías 1 BTU = 1 054 joules |
|
|
