APÉNDICE II

LEY DE DECAIMIENTO RADIACTIVO

Según se vio, la actividad A es proporcional al número de núcleos N presente en la muestra radiactiva en un instante dado, a través de la constante de decaimiento:

A = l N.

Como actividad implica transmutación nuclear, al ir decayendo la muestra con el tiempo, el número N va disminuyendo con una rapidez -dN/dt. El signo negativo indica disminución de N al avanzar el tiempo t. Por lo tanto,

Si tomamos la segunda parte de esta ecuación, tenemos una ecuación diferencial que debe resolverse por separación de variables:

Integrando ambos miembros,

ln N = -lt + K,

en donde K es la constante de integración y In indica el logaritmo natural. Ahora se toma la exponencial en ambos miembros, recordando que la función exponencial es la inversa del logaritmo natural, quedando

N= e^-lt+k = e^-lt x e^K .

Para encontrar el valor de la constante de integración K, supóngase que al iniciar el proceso de decaimiento (t = 0) el valor de N es N₀. Substituyendo estos valores en la ecuación, si t = 0, N = N₀,

N₀ = e^K,

por lo tanto,

N = N_o e^-lt,

que es la ley de decaimiento radiactivo. Indica la forma analítica en que el número de núcleos va disminuyendo con el tiempo.

La actividad correspondiente se obtiene con:

A= lN= lN_oe ^-lt.

Si se define A₀ = lN₀, la ecuación para A toma la misma forma exponencial que la de N, o sea, la actividad disminuye con el tiempo en la misma forma que el número de núcleos:

A = A₀ e ^-lt

La vida media t_1/2 de un isótopo es el tiempo que tarda en disminuir su actividad a la mitad. Si en la ecuación de decaimiento se substituyen los valores cuando t = t_1/2, A =A₀ /2, se obtiene que

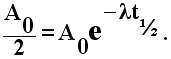
Eliminando A₀ y tomando el inverso,

2 = e-lt_1/2.

Ahora se toma el logaritmo natural en ambos miembros:

ln 2 = 0.693 = lt_1/2

De aquí se obtiene la relación entre la constante de decaimiento y la vida media de un isótopo: