APÉNDICE III
ATENUACIÓN DE RAYOS X Y GAMMA EN LA MATERIA
Refiriéndose a la figura 14, si al absorbedor se le agrega una capa delgada de espesor dx, entonces la intensidad medida en el detector se ve disminuida por una cantidad dI. Se observa, además, que esta disminución es proporcional al coeficiente lineal de atenuación m, a la intensidad misma, y al espesor dx:
La solución de esta ecuación diferencial es semejante a la de la ley de decaimiento radiactivo (Apéndice II), obteniéndose la atenuación exponencial:
Nótese que, si no hay absorbedor, x = 0, y substituyendo en la ecuación queda I = I 0.
La capa hemirreductora x1/2 se obtiene de la misma manera que se obtiene la vida media en la ley de decaimiento. Cuando x = x1/2, I = I0 /2:
Eliminando I 0 tomando logaritmos y despejando, resulta:
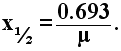
La capa decimorreductora x1/10 corresponde al caso I = I0/10. Siguiendo el mismo procedimiento se encuentra:
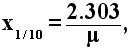
en donde 2.303 es el logaritmo natural de 10.
Como la atenuación se puede deber a una combinación de los tres efectos (fotoeléctrico, Compton y producción de pares), el coeficiente lineal de atenuación puede representarse como una suma de tres coeficientes lineales, cada uno correspondiente a uno de los tres efectos:
Al incorporarse a la ecuación de atenuación, ésta queda:
En ciertos casos puede haber atenuación debida a diversos materiales, por ejemplo aire y plomo. En estos casos se numeran los materiales y se emplea la fórmula:
siendo m1 y m2 los coeficientes lineales dé atenuación de los materiales 1 y 2 respectivamente, y siendo x1 y x2 los espesores de los dos materiales.


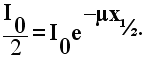 2
2