I. EL MISTERIOSO FLUJO DE LOS L�QUIDOS POLIM�RICOS

"NADA ES, TODO FLUYE", afirm� el fil�sofo griego Her�clito en el siglo V antes de nuestra era... y ten�a raz�n. Si pudi�ramos observar las rocas s�lidas en el interior de la Tierra, el concreto y el acero de las construcciones o el vidrio de los vitrales de una catedral antigua, durante las escalas de tiempo apropiadas, es decir, durante intervalos de tiempo muy grandes, podr�amos comprobar que efectivamente todo puede fluir. Entender de manera precisa qu� significa y c�mo se produce el fen�meno del flujo de la materia tiene gran importancia tanto desde el punto de vista cient�fico fundamental como del pr�ctico. Por ejemplo, el ingeniero en aeron�utica necesita saber c�mo fluye el aire alrededor del ala de un avi�n o el aceite lubricante en el motor. Un ingeniero civil debe poder predecir c�mo se mover� el suelo sobre el que se asientan los cimientos de una construcci�n debido al peso de la misma y un qu�mico que sintetiza pl�sticos necesita saber si sus materiales tienen las caracter�sticas apropiadas para poder moldearlos y darles una forma determinada. Estos son s�lo algunos ejemplos de los numerosos y diversos problemas pr�cticos en donde interviene el fen�meno del flujo de un material. De hecho este fen�meno est� virtualmente presente en casi todos los aspectos tecnol�gicos actuales en los que, de una forma o de otra, algo fluye o se deforma.

Aunque todos tenemos una idea intuitiva de lo que significa que un material cualquiera fluya, para definir de manera m�s precisa lo que es el flujo se�alaremos primero que este fen�meno est� �ntimamente relacionado con otro, el de la deformaci�n. Llamaremos deformaci�n al movimiento de una parte de un cuerpo con respecto a otras partes del mismo y que, como consecuencia, produce un cambio en su forma o tama�o. En otras palabras, una deformaci�n cambia la distancia que existe entre los diferentes puntos de un cuerpo, o m�s espec�ficamente, resulta del desplazamiento de las part�culas (mol�culas, �tomos o iones) de las que est� compuesto el material, las cuales, bajo la acci�n de fuerzas externas, se desplazan ligeramente de sus posiciones originales. En nuestra experiencia diaria, continuamente nos topamos con deformaciones de materiales. As�, el agua de un r�o que fluye se deforma; una liga o banda el�stica que se estira o una cuerda de viol�n que se pulsa tambi�n se deforman. En general, los cuerpos se deforman cuando sobre ellos act�a un esfuerzo, el cual representa la fuerza por unidad de �rea que se produce en un material debida a la acci�n de una fuerza interna o externa que act�a sobre el sistema. El origen de estos esfuerzos puede ser muy diverso; por ejemplo, el calentamiento no uniforme de un material produce una distribuci�n de esfuerzos dentro del mismo, o la deformaci�n misma de un cuerpo genera otros esfuerzos. Sin embargo, aunque las causas que los produzcan sean variadas, los esfuerzos se pueden clasificar en dos grandes grupos: normales y de corte (cortantes). Si los esfuerzos resultan de aplicar fuerzas perpendiculares a la unidad de �rea del material se llaman normales, y dependiendo del sentido de esta fuerza respecto a la superficie, a su vez se clasifican en tensiles o de compresi�n (Figura 1). Si en cualquier punto de un material los esfuerzos son normales y de compresi�n, como ocurre en el caso de un objeto en reposo y totalmente sumergido en un fluido, a este esfuerzo se le llama presi�n hidrost�tica o simplemente presi�n, la cual es un ejemplo de esfuerzo intuitivo y familiar para todos.

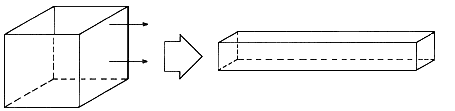
Figura 1. Elongaci�n producida en una muestra de material por un esfuerzo tensil normal.

Por otra parte, los esfuerzos de corte resultan de aplicar fuerzas paralelas y contenidas en el plano de la unidad de �rea de material. En una barra s�lida estos esfuerzos se producen al torcer la barra alrededor de su eje longitudinal, como si se apretara un tornillo (Figura 2). En cambio, en un fluido los esfuerzos de corte se producen, por ejemplo, al deslizar una superficie sobre un l�quido lubricante, o cuando l�quidos y gases resbalan por una superficie s�lida o fluyen por un tubo, o cuando un objeto se mueve en el seno de un fluido, como ocurre durante el paso de un avi�n a trav�s del aire.

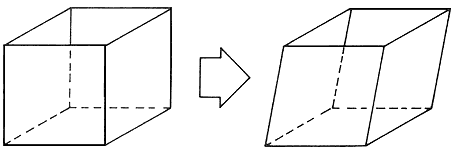
Figura 2. Deformaci�n t�pica producida en un material por un esfuerzo de corte.

Ahora bien, los materiales reaccionan de maneras diferentes ante la acci�n de esfuerzos aplicados. Cuando �stos son peque�os, algunos materiales se deforman y recuperan su forma original al desaparecer los esfuerzos; a estos materiales se les llama s�lidos el�sticos. A diferencia de estos sistemas, los fluidos se caracterizan por ser muy susceptibles frente a la acci�n de los esfuerzos; de hecho, su manera de reaccionar en estas condiciones es lo que define en forma precisa a un fluido: un material incapaz de soportar la acci�n de un esfuerzo de corte. Es decir, por peque�o que sea el esfuerzo aplicado, el fluido experimenta una "deformaci�n continua en el tiempo" o "flujo", y aunque desaparezca el esfuerzo, el fluido no recupera su forma original. Cuando este fen�meno ocurre, las capas de fluido se desplazan unas respecto a otras con velocidades diferentes, como cuando las cartas de una baraja se deslizan unas sobre otras. Sin embargo, los s�lidos el�sticos tambi�n pueden fluir si el esfuerzo aplicado alcanza el valor necesario para que se produzca una deformaci�n permanente. A este valor del esfuerzo se le llama esfuerzo de cedencia del s�lido, y marca la transici�n entre su comportamiento el�stico y el pl�stico, es decir cuando puede fluir. De modo que desde este punto de vista, y dados los esfuerzos necesarios y el tiempo de observaci�n suficiente, �aun los s�lidos pueden fluir!

Ya hemos dicho que un l�quido o gas tiende a fluir bajo la acci�n de un esfuerzo de corte por peque�o que sea, sin embargo, no todos los fluidos fluyen de la misma manera. No hay que olvidar que cualquier fluido real es viscoso, es decir, ofrece una mayor o menor resistencia al deslizamiento relativo de sus capas, que se mueven a velocidad diferente, o sea, que se resiste a deformarse y fluir. En consecuencia, la viscosidad de un fluido necesariamente afecta a la relaci�n que existe entre el esfuerzo aplicado y la deformaci�n producida. Esta relaci�n se expresa por las llamadas relaciones constitutivas, que describen el comportamiento mec�nico de un material de manera aproximada y bajo circunstancias particulares. As�, por ejemplo, una misma barra met�lica puede considerarse completamente r�gida si el esfuerzo aplicado es muy peque�o comparado con el valor de su esfuerzo de cedencia; en cambio, se comportar� como un s�lido el�stico ante valores mayores del esfuerzo aplicado, pero a�n menores que el esfuerzo de cedencia. Pero si el esfuerzo es muy grande se comportar� como un s�lido pl�stico. En cada caso el comportamiento mec�nico est� descrito por una relaci�n constitutiva diferente. La rama de la mec�nica que se ocupa de formular y estudiar las relaciones constitutivas de los materiales es la reolog�a, palabra que proviene del vocablo griego reos, que significa fluir, y es la ciencia que estudia la deformaci�n y el flujo.

Aunque ya desde 1678 el cient�fico ingl�s Robert Hooke hab�a establecido que para una gran variedad de materiales la deformaci�n el�stica producida es proporcional al esfuerzo aplicado, no fue sino hasta 1775 cuando el matem�tico suizo Leonhard Euler propuso la primera relaci�n constitutiva para un fluido, el llamado fluido perfecto o ideal. Este es un fluido cuya fricci�n interna o viscosidad es estrictamente nula y que, adem�s, tiene la siguiente propiedad: el esfuerzo que una parte del fluido ejerce sobre las partes adyacentes es normal; es decir, siempre es perpendicular a la superficie que separa ambas partes. Cualquier fluido real es viscoso en alguna medida y, s�lo en forma aproximada, cuando su densidad es muy baja, se comporta como un fluido ideal. Por ejemplo, el helio a temperaturas muy bajas puede comportarse como el fluido ideal de Euler, con una viscosidad exactamente igual a cero. Como veremos despu�s en el cap�tulo VI, este efecto constituye la base del fen�meno ex�tico de la superfluidez.

La primera relaci�n constitutiva para un fluido viscoso la estableci� Isaac Newton en 1687 al proponer que para estos fluidos el esfuerzo de corte aplicado y la deformaci�n producida son proporcionales, es decir, a mayor esfuerzo mayor deformaci�n. Como ya hemos visto, la deformaci�n implica que la velocidad relativa de las capas de fluido no es la misma, por lo tanto la relaci�n de Newton tambi�n puede expresarse diciendo que el esfuerzo de corte y el cambio de la velocidad en el fluido son proporcionales. A la constante de proporcionalidad se le define como la viscosidad del fluido; por esta raz�n a esta relaci�n constitutiva lineal tambi�n se le llama ley de la viscosidad de Newton. A los fluidos cuyo comportamiento mec�nico se describe adecuadamente en t�rminos de esta relaci�n constitutiva se les llama fluidos newtonianos. El agua y el aire, que son los fluidos m�s abundantes de la Tierra, se comportan como newtonianos con una excelente aproximaci�n. Estos fluidos tambi�n son los m�s estudiados y los mejor comprendidos; a las ecuaciones que gobiernan su movimiento (flujo) se les conoce como las ecuaciones de Navier-Stokes y fueron formuladas desde mediados del siglo pasado por el ingeniero franc�s Louis Marie Navier y por el f�sico ingl�s George Gabriel Stokes. La descripci�n del flujo basada en estas ecuaciones result� muy exitosa, pues ha permitido entender muchos fen�menos y conduce a predicciones que se comparan muy bien con el experimento. Sin embargo, a�n persisten problemas te�ricos y pr�cticos que no han podido resolverse. Es conveniente subrayar que, seg�n la relaci�n de Newton, no s�lo las magnitudes de la "causa" (esfuerzo aplicado) y el "efecto" (deformaci�n o flujo) son proporcionales, sino que la relaci�n entre ellas tambi�n es "instant�nea''. Esto significa que al flujo en el instante de observaci�n s�lo contribuye el esfuerzo aplicado en el mismo instante de tiempo. Los esfuerzos que hayan existido en el fluido en tiempos anteriores no contribuyen a producir la deformaci�n en el momento de la observaci�n. En otras palabras, los fluidos newtonianos no guardan "memoria" de las deformaciones previas.

La experiencia ha demostrado que la gran variedad de l�quidos y gases newtonianos tienen una caracter�stica com�n, a saber, las mol�culas que los componen son ligeras, es decir, de bajo peso molecular. Como su nombre lo indica, el peso molecular es una medida del peso de una mol�cula con respecto a un patr�n de referencia, el cual para todo prop�sito pr�ctico se escoge como el peso de un �tomo de hidr�geno, y que puede tomarse como la unidad. En consecuencia, el peso molecular de una sustancia es un n�mero que representa en forma aproximada, el n�mero de veces que el peso de la mol�cula en cuesti�n excede el peso de un �tomo de hidr�geno. Puede decirse entonces que la relaci�n constitutiva de Newton describe bien el flujo de fluidos cuyas mol�culas tienen pesos moleculares m�ximos de 1 000, aproximadamente. Sin embargo, cuando las mol�culas de un fluido son muy pesadas, por ejemplo con pesos moleculares mayores de 100 000, la ley de viscosidad de Newton ya no describe adecuadamente el flujo de estos fluidos; las relaciones constitutivas ya no son tan simples, pues dejan de ser instant�neas, aunque todav�a pueden ser lineales. A esta clase de fluidos se les llama "no newtonianos".

Quiz� el ejemplo m�s t�pico y m�s com�n de un fluido no newtoniano sea un fluido polim�rico. La caracter�stica esencial de estos sistemas es que sus mol�culas son muy pesadas, con pesos moleculares entre 100 000 y 100 000 000, por eso se les llama macromol�culas. Los pol�meros tienen gran importancia en la vida y la civilizaci�n humanas. Todas las formas de vida dependen de materiales polim�ricos como los �cidos nucleicos, las prote�nas, los carbohidratos, etc. Tambi�n desde tiempos remotos muchos materiales polim�ricos se han usado para satisfacer diversas necesidades humanas. Entre estos materiales pueden mencionarse la madera, resinas naturales, hules, fibras como la lana, la seda o el algod�n, etc. Por otra parte, muchos minerales, como el cuarzo y el diamante, son pol�meros inorg�nicos y una gran variedad de productos de la industria moderna, como el concreto, la porcelana, las fibras textiles, el vidrio, hules y pl�sticos, son pol�meros puros o est�n compuestos en gran parte por pol�meros. La palabra pol�mero se deriva de dos vocablos griegos, polys que significa muchos y meros, parte o unidad. Como su nombre lo indica, las mol�culas de un pol�mero est�n formadas por muchas unidades o mon�meros de bajo peso molecular que se mantienen unidos entre s� por fuerzas intermoleculares muy intensas llamadas enlaces covalentes. El proceso mediante el cual estas unidades se unen sucesiva y repetidamente para formar cadenas largas y pesadas (macromol�culas), se llama polimerizaci�n (Figura 3).

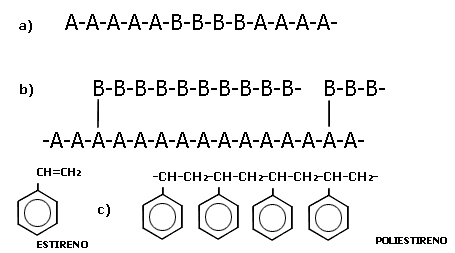
Figura 3. (a) Polimerizaci�n lineal, (b) polimerizaci�n ramificada, (c) polimerizaci�n del estireno.

A diferencia de los fluidos newtonianos, el estudio de la din�mica de los fluidos polim�ricos es relativamente reciente, pues se inici� alrededor de 1950 motivado, precisamente, por el vertiginoso desarrollo de la industria de los pl�sticos. Y aunque es un campo de investigaci�n muy activo, a�n est� en proceso de desarrollo. La din�mica de los fluidos polim�ricos pretende, a un nivel macrosc�pico, construir las relaciones constitutivas apropiadas que permitan describir y entender, por ejemplo, los flujos y fen�menos asociados con las aplicaciones industriales de los mismos. Hemos mencionado, sin justificarlo, que la relaci�n constitutiva lineal de Newton es inadecuada para describir el flujo de l�quidos polim�ricos. Pero podr�amos leg�timamente preguntarnos cu�l es esta evidencia experimental, cu�les son los hechos bien establecidos que irremisiblemente nos obligan a generalizar la descripci�n din�mica de los fluidos newtonianos. La respuesta a esta pregunta es que, efectivamente, existen numerosos experimentos que claramente indican que el flujo de los fluidos newtonianos es cualitativamente diferente al de los polim�ricos. Veamos gr�ficamente estas diferencias para lo cual en lo que sigue tomaremos al agua como prototipo de fluido newtoniano.

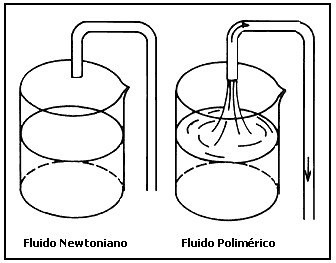
Todos conocemos el efecto del sif�n, lo practicamos al beber un l�quido ordinario con un popote: el liquido fluye a trav�s de �l en tanto que uno de sus extremos est� dentro del l�quido. Para nuestra sorpresa, si en vez de agua tenemos un fluido no newtoniano se observa que el efecto de sif�n puede ocurrir aunque el tubo de succi�n no est� inmerso en �l. De modo que un fluido polim�rico puede succionarse aun y cuando existan varios cent�metros de separaci�n entre la superficie del fluido y el extremo del tubo. A este efecto se le conoce como sif�n sin tubo (Figura 4).

Figura 4. Efecto de sif�n.

Figura 5. Efecto Weissenberg.

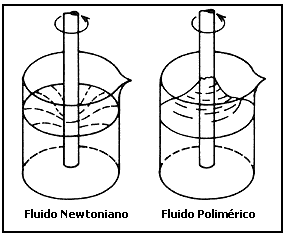
En la figura 5 observamos que si ponemos agua en un vaso de precipitados y lo agitamos a una velocidad moderada con un agitador cil�ndrico, en la superficie del agua alrededor del agitador se produce una depresi�n. En realidad el efecto podr�a haberse anticipado, pues por la acci�n del agitador el agua tambi�n empieza a girar y la fuerza centrifuga tiende a desplazarla hacia las paredes del recipiente. El resultado neto es acumular fluido en las paredes y producir una deficiencia alrededor del cilindro, la cual se manifiesta en la depresi�n central. Sin embargo, esta explicaci�n intuitiva es inv�lida si el fluido es polim�rico. En este caso sucede precisamente el efecto contrario: el fluido no s�lo se concentra alrededor del agitador �sino que tambi�n trepa por �l! A este fen�meno se le conoce como efecto Weissenberg y fue descubierto por Karl Weissenberg en Inglaterra durante la segunda Guerra Mundial.

Si ahora repetimos el experimento anterior pero haciendo girar en el fondo del vaso un disco de di�metro igual al del recipiente, observamos que la superficie del agua se deprime, en tanto que en el caso del l�quido polim�rico se produce una protuberancia en su superficie (Figura 6). Una variante de este experimento consiste en hacer girar el mismo disco en la superficie del l�quido. Para ambos fluidos observamos que se superponen dos flujos. El flujo primario es tangencial al disco y sigue la direcci�n de su rotaci�n. Pero el flujo que se superpone a �ste, y que llamaremos secundario, es diferente en ambos casos. En el agua, el disco en rotaci�n tiende a desplazar al l�quido hacia las paredes y luego, cerca de ellas, realiza un giro hacia el fondo del vaso para finalmente emerger hacia arriba cerca del eje de rotaci�n del disco. En el caso del fluido polim�rico, el flujo secundario es id�ntico en naturaleza, pero ocurre en sentido contrario: �baja por el eje y gira para subir por las paredes!. Este efecto fue observado por primera vez por C.T. Hill en 1972 (Figura 7).

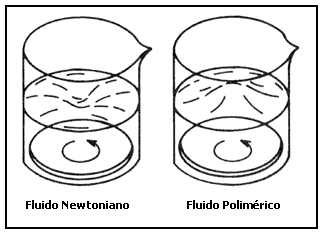
Figura 6. Efecto de depresi�n superficial.

 

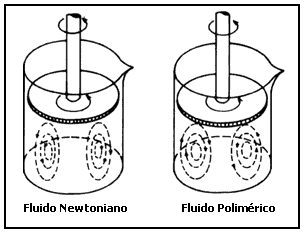
Figura 7. V�rtices interiores.

Una de las diferencias m�s notables entre los fluidos newtonianos y los polim�ricos es que los �ltimos tienen "memoria". Como ya mencionamos antes, esto significa que la deformaci�n del material a un cierto instante de tiempo depende no s�lo de los esfuerzos aplicados en ese instante, sino tambi�n de las deformaciones y esfuerzos previos. Esta caracter�stica se observa en otro experimento en el que tales fluidos se "bombean" a lo largo de un ducto cil�ndrico horizontal.

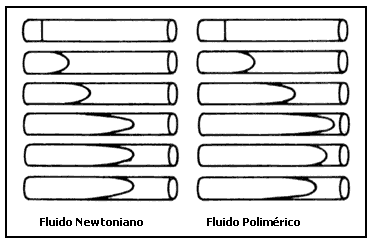
Imaginemos que ponemos ambos fluidos en tubos de vidrio y que, al momento de introducirlos en ellos, agregamos una traza de colorante para poder observarlos f�cilmente. Ahora supongamos que seguimos el movimiento del colorante por un tiempo durante el cual lo fotografiamos, y despu�s apagamos la bomba. Primero vemos que la marca inicial de colorante se deforma, pues el fluido se mueve m�s r�pido en el centro del tubo que cerca de sus paredes. Adem�s, notamos que, en el caso del agua, �sta simplemente se detiene al desconectar la bomba, lo que concuerda con lo que, intuitivamente esperamos, esto es, que al desaparecer la causa que produce las deformaciones, el fluido ya no se deforma. Sin embargo, no es esto lo que ocurre en el caso del fluido polim�rico, donde se observa que aparece un efecto de retroceso, una tendencia a regresar a situaciones previas y gradualmente pasa al estado de reposo. Claramente, esto significa que, aun despu�s de haber desconectado la bomba, el fluido polim�rico sigue deform�ndose, pero ahora en sentido inverso debido a los esfuerzos que se produjeron en tiempos anteriores al de detener la bomba. Esta es una manifestaci�n de la memoria del fluido y en reolog�a se le llama efecto de memoria desvaneciente, pues se observa que el fluido no recupera totalmente sus configuraciones previas, lo que significa que la memoria se desvanece (relaja) a medida que el tiempo transcurre. Aqu� mostramos gr�ficamente este efecto en la figura 8, donde los perfiles con l�neas oscuras representan, de forma esquem�tica, el comportamiento del fluido antes de y en el momento de desconectar la bomba.

Figura 8. Efecto de memoria.

Otro efecto un tanto sorprendente es el comportamiento que exhibe un fluido polim�rico al emerger de un orificio. En el caso del agua, �sta no se expande ni se contrae, pero un líquido polim�rico puede "hincharse" y aumentar su secci�n transversal �hasta por un factor de cinco! De hecho, este efecto podemos observarlo f�cilmente al oprimir un tubo de pasta dental (Figura 9).

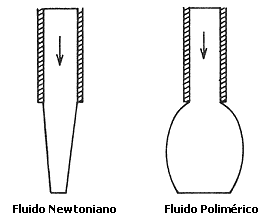
Figura 9. Efecto de hinchamiento.

Pero hay todav�a otros efectos, no menos sorprendentes, que son f�ciles de observar. Imaginemos que llenamos con agua un tubo relativamente ancho el cual est� conectado por uno de sus extremos a otro tubo de di�metro menor, y que dejamos que el agua fluya lentamente del primero al segundo cuando est�n colocados verticalmente. En el caso del agua no vemos otra cosa, aparte de que �sta aumenta su velocidad al pasar al tubo m�s angosto. En cambio, con el fluido polim�rico observamos que se forman peque�os v�rtices (remolinos) en la vecindad de la conexi�n entre ambos tubos. Las part�culas de fluido atrapadas en ellos nunca caen al tubo menor. �Qu� magn�fico espect�culo ser�a contemplar una catarata producida por un flujo polim�rico! Este efecto se muestra esquem�ticamente en la figura 10.

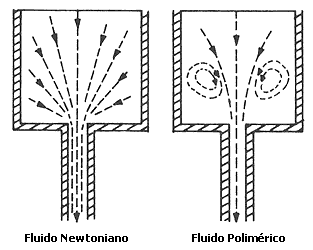
Figura 10. Efectos de v�rtice a la salida de un recipiente.

Finalmente, otro efecto no menos impresionante se observa si en un tubo de ensayo que contenga un l�quido arrojamos dos esferas, una despu�s de la otra. En el caso del agua observamos que la segunda siempre precede a la primera y choca con ella. Int�ntelo el lector con dos esferas no muy pesadas. Pero si ahora repetimos la experiencia con un l�quido polim�rico, ocurre lo mismo si la segunda esfera se arroja inmediatamente despu�s de la primera, pero para cada fluido existe un tiempo cr�tico despu�s del cual �las esferas tienden a separarse mientras caen! Otra vez, el l�quido percibe o guarda memoria del efecto producido por la perturbaci�n inicial (Figura 11).

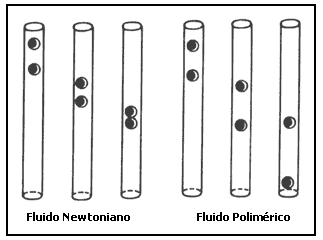
Figura 11. Nuevamente los efectos de memoria.

No debe olvidarse que, adem�s de los pol�meros, existen otros fluidos no newtonianos muy importantes como la sangre, diversos tipos de suspensiones o incluso el magma del interior de la Tierra. Estos fluidos tambi�n muestran efectos reol�gicos sorprendentes. Para mencionar s�lo uno de ellos recordemos primero que l�quidos newtonianos como el agua, el alcohol, el tolueno o una soluci�n de az�car en agua, tienen viscosidad constante. En consecuencia, la raz�n temporal de cambio o tasa de sus flujos es directamente proporcional a la presi�n que los hace fluir de acuerdo con la ley de viscosidad de Newton. En contraste con este comportamiento, se observa que cuando se hace fluir sangre por un tubo, al duplicar la presi�n la tasa de flujo no se duplica sino que se incrementa en forma no lineal por un factor de 3 o 4. En otras palabras su viscosidad es menor cuando la sangre fluye a bajas presiones.

Todos estos experimentos ilustran un punto crucial: frente a las mismas causas la respuesta de un fluido polim�rico es cualitativamente diferente a la de un fluido newtoniano. La reología ha comprobado que estas diferencias de comportamiento din�mico pueden entenderse y explicarse cambiando tanto la relaci�n constitutiva lineal de Newton como las ecuaciones de Navier-Stokes. Aqu� vamos a intentar explicar someramente, y sin recurrir a ning�n artificio matem�tico, c�mo se procede para lograr este fin. Por un momento si�ntase el lector "una part�cula de fluido". Dotado de unos buenos tanques de ox�geno y sin aletas d�jese arrastrar por la corriente. Otras part�culas del fluido lo perturban alterando su velocidad con el tiempo, tanto en direcci�n como en magnitud. Como cualquier otra part�cula del fluido, usted tambi�n tiene una masa finita, de modo que podemos hablar de cu�nta masa, cu�nto �mpetu (igual a masa por velocidad), qu� tanta energ�a cin�tica (masa por el cuadrado de la velocidad) y cu�nta energ�a de cualquier otra �ndole, que llamaremos energ�a interna (usted se desgastar� por chocar con otras part�culas, al vencer la resistencia que le oponen sus vecinos al moverse por el fluido, etc.), transporta o carga sobre sus espaldas en el transcurso del tiempo. Bueno, pues usando principios muy generales de la f�sica, se pueden obtener las llamadas ecuaciones de conservaci�n de todas estas cantidades: en ausencia de fuentes y sumideros, la masa y la energ�a se conservan, y en ausencia de fuerzas externas el �mpetu se conserva. Pero estas ecuaciones tienen cinco variables: las que usted "part�cula de fluido" porta consigo mismo, la masa, el �mpetu y la energ�a. Pero resulta que en las correspondientes ecuaciones hay catorce inc�gnitas.

Si por el momento despreciamos efectos t�rmicos, esto es, p�rdida de calor, y suponemos que la temperatura es constante, todav�a nos quedan diez inc�gnitas y cuatro ecuaciones, una para la masa y tres para el �mpetu (la velocidad es un vector). Luego, entonces, para tener un sistema matem�ticamente completo se requiere de seis ecuaciones adicionales. Estas ecuaciones constituyen la forma m�s general en que puede expresarse la f�rmula de Newton que define a la viscosidad, y nos permitir�a expresar al flujo de �mpetu que aparece en la ecuaci�n, para el �mpetu mismo, en t�rminos de la velocidad. Estas ecuaciones, que describen la respuesta de un medio ante un efecto externo y la expresan en t�rminos de las propias variables que describen el estado del sistema, la velocidad del fluido en �ste caso, son las ecuaciones constitutivas.

Pues bien, el reto en el caso de los fluidos polim�ricos radica precisamente en encontrar cu�les son las relaciones constitutivas para condiciones de flujo bien definidas. Estas ecuaciones deben reflejar todas las caracter�sticas que encontramos en los experimentos anteriores y muchas m�s que hemos omitido. S�lo para ilustrar el grado de dificultad del problema pensemos en un fluido polim�rico con memoria desvaneciente. Supongamos, para facilitar las cosas, que el flujo es isot�rmico, lo que significa que la temperatura es constante y pueden despreciarse los efectos causados por la generaci�n de calor. La relaci�n constitutiva correspondiente, aun en el supuesto caso de que subsista una relaci�n entre causa y efecto, ya no puede ser instant�nea, esto es, v�lida en cada instante de tiempo. En efecto, si a un tiempo inicial t_o perturbamos al fluido, el efecto de esta perturbaci�n se dejar� sentir en todo tiempo posterior t mayor que t_o hasta desvanecerse por completo despu�s de transcurrido un cierto intervalo de tiempo, llamado tiempo de relajaci�n, del sistema. Durante todo intervalo, el fluido recoge la informaci�n de c�mo se propaga la perturbaci�n hasta que el efecto desaparece. Esto conduce a expresiones matem�ticas que son no locales en el tiempo, es decir, no son instant�neas y se conocen como funciones de memoria. Su obtenci�n y la caracterizaci�n de sus propiedades matem�ticas constituye uno de los grandes problemas de la reolog�a.

Sin embargo, en la mayor parte de los procesos industriales la mayor�a de los problemas que se presentan se complican por la presencia de transferencia de calor. Esto implica que la ecuaci�n de conservaci�n de energ�a debe acoplarse con la del �mpetu y la de masa, de manera que la complejidad f�sica inherente a la estructura de las ecuaciones constitutivas aumenta considerablemente. �Y no digamos el problema matem�tico resultante! Los efectos de la temperatura en estos procesos reol�gicos apenas comienzan a explorarse y debemos esperar en estos campos un progreso considerable en un futuro cercano.

Antes de cerrar este cap�tulo es pertinente hacer una breve consideraci�n sobre el aspecto molecular de los fluidos polim�ricos. Con esto queremos decir c�mo interpretar sus sorprendentes caracter�sticas descritas antes y c�mo poder deducir las relaciones constitutivas que los gobiernan a partir de las leyes que rigen el comportamiento de los �tomos o mol�culas que los forman. Si la arquitectura de los s�lidos y l�quidos simples ya es un problema complicado¹ , en el caso de los pol�meros esta complicaci�n se acrecienta enormemente.

A nivel molecular (microsc�pico) hay diferencias importantes entre los fluidos newtonianos, compuestos por mol�culas peque�as, y los fluidos macromoleculares o polim�ricos. Diversas caracter�sticas de la arquitectura macromolecular influyen y determinan sus propiedades de flujo. Entre ellas la primera, que ya hemos mencionado, es el gran peso molecular de las mol�culas que los componen. En segundo t�rmino debe se�alarse que rara vez los mon�meros que componen un pol�mero tienen el mismo peso molecular, m�s bien son mezclas que tienen una distribuci�n de pesos moleculares. El hecho es importante, pues se observa que las propiedades reol�gicas son muy sensibles a esta diversidad de pesos moleculares. Otra caracter�stica esencial es que, aun sin fluir, las mol�culas polim�ricas pueden adoptar un n�mero enorme de configuraciones, y como el flujo las altera estirando o alineando las mol�culas, los cambios de configuraci�n a su vez influyen en las propiedades en flujo. Cuando las concentraciones de pol�mero son altas, las mol�culas forman redes muy enmara�adas cuya configuraci�n cambia con el tiempo y con las condiciones de flujo. Puede uno imaginarse que tal entrecruzamiento din�mico de mol�culas polim�ricas se asemeja a un barril lleno de serpientes excitadas que se mueven y se enredan entre s�. En esas condiciones, para poder separarse unas de otras las mol�culas, como las serpientes, deben "reptar", es decir, deben seguir trayectorias tortuosas, lo que produce una viscosidad grande y dependiente de la longitud del pol�mero. Esta comparaci�n tambi�n permite intuir que los efectos de memoria aparecen porque a las mol�culas enmara�adas les toma tiempo ajustarse o responder a la acci�n de un esfuerzo, por eso su respuesta no es instant�nea.

Estudiar microsc�picamente estos sistemas no es tarea f�cil, pero el ingenio no conoce l�mites y se ha podido desarrollar una teor�a cin�tica (microsc�pica) de los fluidos polim�ricos, representados, modestamente, por un conjunto de cuentas y resortes. Los primeros representan las unidades qu�micas que componen el pol�mero y las segundas las fuerzas que las unen (Figura 12). No es el presente libro el lugar apropiado para intentar explicar algunos detalles de esta teor�a; baste decir que, a pesar de lo poco refinado del modelo, los resultados hasta ahora obtenidos son lo suficientemente razonables como para indicar que por lo menos el camino escogido es el correcto. Es un campo fascinante de investigaci�n de frontera, no s�lo por la concepci�n misma de establecer una correlaci�n te�rico-experimental de las propiedades fisicoqu�micas de aquellos sistemas, sino adem�s porque constituyen la base de muchos procesos biol�gicos e industriales. Todav�a se requiere de mucha investigaci�n de avanzada para poder resolver los problemas relacionados con el procesamiento de los pl�sticos, para mejorar la acci�n de los lubricantes, de las pinturas o para entender el movimiento de los fluidos biol�gicos. Todos ellos son retos para el futuro.

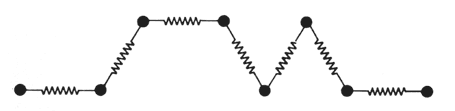
Figura 12. Modelo de una cadena polim�rica lineal y flexible.