I. LUZ Y MATERIA

EL DESARROLLO del láser, como el de cualquier otro descubrimiento importante, fue posible gracias a los avances previamente logrados en otras disciplinas científicas. En el caso que nos ocupa, estas disciplinas las encontramos fundamentalmente en la física moderna y, en particular, en la parte de ésta llamada mecánica cuántica. A su vez, el germen que dio origen a la mecánica cuántica lo encontramos en el siglo XIX, cuando los científicos de la época trataron de encontrar la distribución del espectro emitido por un cuerpo caliente. Por tanto comenzaremos nuestra exposición aquí.

RADIACIÓN TÉRMICA

Si calentamos un objeto a 200ñ C podremos notar al acercar la mano a éste que emite cierta radiación invisible llamada calor o radiación infrarroja. Si ahora aumentamos la temperatura del objeto hasta 600ñ C (la que produce por lo común una estufa eléctrica) notaremos que una tenue luz roja empieza también a ser emitida. Aumentando la temperatura del objeto a 2 000ñ C (la del filamento interno de un foco eléctrico) emitirá radiación visible de color amarillo y si seguimos aumentando continuamente la temperatura el color que observaremos será progresivamente, azul, violeta, etc. Este es un resultado fácil de comprobar.

La figura I.1 muestra el espectro electromagnético, indicando la región del espectro que nos es visible, y la figura I.2 muestra los resultados experimentales observados al realizar un experimento como el anteriormente descrito. En esta figura aparece la intensidad de radiación emitida por longitud de onda para varias temperaturas.

 

Figura I.1. Líneas de potencia

Podemos observar que, a medida que aumenta la temperatura del cuerpo, el punto máximo de intensidad se desplaza hacia longitudes de onda cada vez menores. Este hecho se conoce como la ley de desplazamiento de Wien. Asimismo, de la figura I.2 podemos notar que la energía total emitida por un cuerpo caliente a una temperatura T es proporcional al área contenida bajo la curva a esa temperatura. Entre más caliente esté el cuerpo, más energía en forma de radiación emite. Este resultado es la ley de Stefan-Boltzmann, que expresa que la energía total irradiada por un cuerpo con una temperatura T aumenta en forma proporcional a la cuarta potencia de la temperatura a que se encuentra.

Uno de los resultados más sorprendentes de este problema radica en que los resultados experimentales graficados en la figura I.2 no dependen de la naturaleza o forma del cuerpo en cuestión. Esto significa, por ejemplo, que si tenemos dos trozos de forma arbitraria, uno de platino y otro de acero, y los calentamos, la gráfica de intensidad de radiación emitida por longitud de onda (como la de la figura I.2) para varias temperaturas tendrá las mismas características generales en ambos casos.

El problema al que se enfrentaron los científicos de fines del siglo XIX fue tratar de explicar teóricamente los resultados experimentales mostrados en la figura I.2. Su problema era construir un modelo teórico-matemático capaz de reproducir las observaciones experimentales. Claro está, inicialmente la herramienta de que ellos se valieron fue la física y la matemática entonces conocidas (ñno tenían otra alternativa!). En particular, hicieron uso de la física estadística que había sido previamente desarrollada por Ludwing Boltzmann, James Clerk Maxwell, Josiah Willard Gibbs y algunos otros.

Un científico que trabajó intensamente en tratar de resolver el problema de la radiación térmica emitida por un cuerpo caliente fue James Jeans, quien planteó el problema esencialmente de la siguiente manera: dado que las leyes de la física estadística nos permiten determinar con precisión la distribución de energía de las moléculas de un gas y puesto que se quiere obtener la distribución de energía emitida por longitud de onda por un cuerpo caliente entonces sólo debemos aplicar los mismos métodos estadísticos a ambos problemas.

 

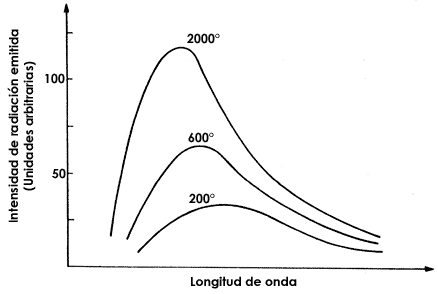
Figura I.2.

Para ver el problema central al que se enfrentó Jeans realicemos el siguiente "experimento pensado" (Gedankenexperiment es el término original en alemán). Este tipo de experimentos, como su nombre lo indica, no son realizados físicamente sino sólo "pensados". En ellos se aplican las leyes físicas conocidas y se deduce el resultado que obtendríamos si realizáramos el experimento.

Consideremos dos cubos huecos rectangulares de dimensión L por lado. En el primero introduciremos algunas moléculas de gas y en el segundo introduciremos radiación electromagnética de cierta longitud de onda l. Debemos añadir que las paredes internas de este último cubo están hechas de un material capaz de absorber (y por lo tanto de emitir) radiación de cualquier longitud de onda. Es decir, la radiación electromagnética contenida allí será indefinidamente absorbida y reemitida por las paredes del cubo.

Al cabo de un cierto tiempo y debido a la transferencia de energía cuando las moléculas chocan unas contra otras, la distribución de energía de las moléculas contenidas en el primer cubo estará dada por las leyes de la física estadística. La energía promedio de cada molécula será igual a la energía total disponible E, dividida entre el número total de moléculas N. Este resultado es conocido como la ley de equipartición de energía, y es un resultado básico de la física estadística.

Si nosotros observáramos el espectro de radiación electromagnética contenido en el segundo cubo, veríamos que —como ya sabemos— es un espectro continuo cuya forma exacta está determinada por la temperatura a que se encuentran las paredes del cubo. Así, la energía de la radiación electromagnética inicialmente introducida en el cubo, debió distribuirse en los varios modos posibles de oscilación dentro de éste.

Por simplicidad supongamos ahora un "cubo" unidimensional de longitud L. Si la longitud de onda de la radiación inicialmente introducida fue l =  L vemos que los modos posibles de oscilación dentro del "cubo" son aquellos que tengan longitudes de onda l/2, l/3, l/4,..., etc., esto es, longitudes de onda cada vez más cortas.

Como vemos, el número de tales modos posibles de oscilación es infinito y, por lo tanto, si aplicamos la ley de equipartición de energía de la física estadística obtendremos que la energía promedio por modo de oscilación es nula, pues el número de grados de libertad es infinito.

Aún más, su hubiéramos introducido, por ejemplo, luz roja en el cubo, ésta se hubiera convertido progresivamente en luz azul, violeta, ultravioleta, rayos X, rayos gamma, y así sucesivamente, sin límite alguno. Por lo tanto, al abrir el horno de la cocina deberíamos morir instantáneamente al ser alcanzados por una mortífera radiación de muy corta longitud de onda. Este hecho, conocido como la "catástrofe ultravioleta", mostró la incapacidad de la física del siglo XIX —ahora llamada física clásica— para resolver algunos problemas importantes.

Para todo el mundo quedó entonces claro que si se quería evitar la catástrofe ultravioleta deberían realizarse cambios radicales en los modelos de la física clásica hasta entonces aceptada.

LOS CUANTA DE ENERGÍA

El problema de la radiación térmica también conocido como el problema del "cuerpo negro", fue resuelto por Max Planck en el año de 1900. Así se inició una de las más importantes ramas de lo que ahora llamamos física moderna. Planck halló la solución al postular que la energía de una onda electromagnética (o cualquier otro sistema oscilante) puede existir en forma de paquetes llamados cuanta. La energía E de cada cuanta es directamente proporcional a la frecuencia de oscilación. Esto es

E = hv

donde h es una constante universal, hoy conocida como constante de Planck y que vale h = 6.6256 x 10^-34 joules-segundo.

Con esta suposición y haciendo uso de la física estadística se puede ahora calcular la distribución de energía emitida por longitud de onda por un cuerpo a la temperatura T. El resultado es una expresión matemática que concuerda maravillosamente con los resultados experimentales mostrados en la figura I.2. ñEl problema del cuerpo negro estaba así resuelto!

Aunque Planck tuvo la necesidad de postular la cuantificación de la energía, él no creía realmente en la existencia física de tales paquetes energéticos. Sin embargo la evidencia experimental mostró, en efecto, que un sistema físico no puede intercambiar cantidades arbitrarias de energía sino sólo cantidades cuantizadas. Asimismo, dicha evidencia experimental mostró que los cuanta se comportan como partículas. Es decir, los cuanta no eran sólo un recurso matemático que permitió resolver un problema, sino entes físicos reales. Dos importantes experimentos que apoyaron decididamente esta idea fueron el efecto fotoeléctrico y el efecto Compton; el primero fue explicado por Albert Einstein en 1905 y el segundo por Arthur H. Compton en 1923.

ÁTOMOS Y TRANSICIONES ELECTRÓNICAS

El primer modelo "moderno" del átomo fue proporcionado por Ernest Rutherford. Este modelo estaba basado en sus resultados experimentales que mostraban conclusivamente que el átomo está formado por un núcleo muy masivo con carga positiva, alrededor del cual giraban los electrones, con carga negativa, formando un sistema similar a un pequeño sistema planetario. El problema fundamental de este modelo estaba en que, de acuerdo con la teoría electromagnética clásica, una partícula cargada como un electrón, girando en una órbita, debería radiar ondas electromagnéticas y perder así rápidamente toda su energía. Es decir, un átomo sería un sistema inestable en el cual sus electrones se colapsarían siguiendo órbitas espirales hacia el núcleo atómico y emitiendo en el proceso un breve destello de radiación electromagnética de una cienmillonésima de segundo. El universo, tal como lo conocemos, no podría existir. Nuevamente, como en el problema de la radiación térmica, la física clásica era incapaz de proporcionar una respuesta congruente con la observación experimental.

Quien solucionó en 1913 esta paradójica situación fue el físico Niels Bohr al proponer un modelo atómico en el cual los electrones únicamente pueden encontrarse en un número discreto de órbitas alrededor del núcleo; para que un electrón pase de una órbita a otra debe emitir (o absorber, según el caso) un cuanto de energía. Así, Bohr sintetizó con su modelo los resultados experimentales de Rutherford y las proposiciones teóricas de Planck.

La figura I.3 muestra la estructura de un átomo de acuerdo con la teoría de Bohr. En este ejemplo tenemos que un electrón puede encontrarse solamente en una de las cinco órbitas mostradas. Para que el electrón pase de la primera a la segunda órbita necesita recibir un cuanto con energía exactamente igual a la diferencia de energía entre la primera y la segunda órbita. Igualmente, el paso de un electrón de una órbita superior a otra inferior sólo será posible si éste emite un cuanto con energía igual a la diferencia de energía entre dichas órbitas.

 

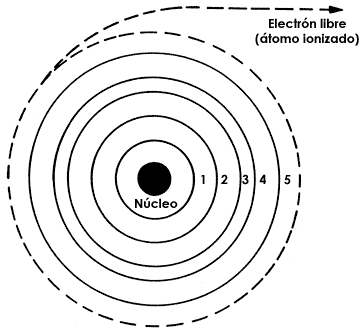
Figura I.3.

Nótese que si el electrón se encuentra en la primera órbita no podrá emitir ningún cuanto de energía puesto que ya no hay órbitas de menor energía a las cuales pueda descender. Por otra parte, también debe observarse que a partir de la última órbita (en el caso de la figura, la 5ñ. órbita), si el electrón recibe otro cuanto de energía éste pasará a ser un "electrón libre" y se separará del átomo, pues ya no hay más órbitas superiores a las cuales pasar. Entonces decimos que el átomo está ionizado, esto es, se ha convertido en un átomo que ha perdido uno o varios de sus electrones.

El modelo de Bohr explicó los espectros de emisión de átomos simples como el hidrógeno y el helio, y proporcionó las bases para comprender el espectro de átomos más complejos. Claro está, la física atómica no se detuvo allí; pronto este modelo fue incapaz de explicar nuevas observaciones experimentales y como consecuencia tuvo que ser mejorado. No obstante, las ideas esenciales del modelo atómico de Bohr que hemos expuesto son suficientes para comprender lo que veremos a continuación.

INTERACCIÓN ÁTOMO-CUANTO

Ahora enunciaremos los procesos básicos de interacción entre la materia y la radiación electromagnética que en su más pequeña escala se reducen a los procesos de interacción entre átomos y cuantos de energía de radiación electromagnética.

Supondremos un sistema atómico elemental con dos niveles de energía E₁ y E₂ en el cual el primer nivel corresponde a un electrón en su órbita inferior y el segundo nivel corresponde a un electrón en su órbita superior. En el primer caso diremos que el átomo se encuentra en su estado base y en el segundo caso en su estado excitado. Como vimos en la sección anterior, este sistema atómico sólo podrá interaccionar con cuantos que tengan una energía E igual a la diferencia de energía E = E₂ - E₁. Por lo tanto, la frecuencia v asociada a dichos cuantos de energía es

	E2 - E1
v     =
	h

 

En tal caso diremos que la interacción átomo-cuanto es un proceso resonante. En este libro sólo consideraremos interacciones resonantes.

Por brevedad, de ahora en adelante llamaremos fotón a un "cuanto de radiación electromagnética". El término fotón fue introducido por Einstein al estudiar el efecto fotoeléctrico.

El primer proceso de interacción átomo-fotón que veremos es el proceso de absorción, que se muestra esquemáticamente en la figura I.4. Consiste en la interacción entre un fotón y un átomo que inicialmente se encuentra en su estado base. El resultado de esta interacción es que el átomo "absorbe" al fotón y usa su energía para pasar a su estado excitado.

 

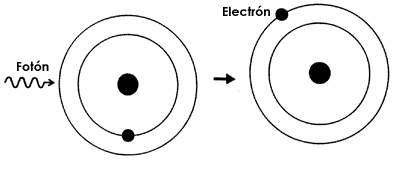
Figura I.4. Absorción

El siguiente proceso importante de interacción átomo- fotón es el proceso de emisión espontánea, el cual se muestra esquemáticamente en la figura I.5. Ahora tenemos un átomo ya excitado inicialmente, que en forma espontánea (y generalmente en un tiempo breve, del orden de 10-8 segundos) pasa a su estado base emitiendo en el proceso un fotón con energía igual a la diferencia de energía entre los dos estados. El fotón se emite en una dirección totalmente aleatoria.

 

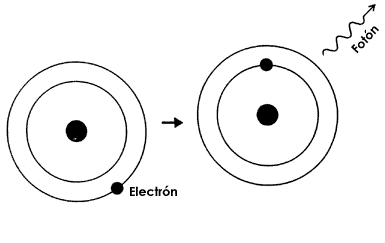
Figura I.5. Emisión espontánea

Finalmente, el otro proceso importante de interacción átomo-fotón es el proceso de emisión estimulada. Su existencia fue propuesta por Albert Einstein en 1917 y es el proceso fundamental gracias al cual existe el láser. La figura I.6 muestra esquemáticamente tal proceso. En él tenemos la interacción entre un fotón y un átomo que inicialmente se encuentra en su estado excitado. Como resultado de esta interacción el átomo pasa a su estado base emitiendo en el proceso un fotón que tiene las mismas características de dirección y de fase que el fotón inicial. Por lo tanto, decimos que la radiación electromagnética que resulta es coherente.

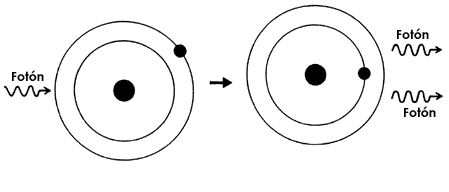
Figura I.6. Emisión estimulada

Podemos realmente afirmar que el germen que dio origen al desarrollo del láser fue dado a la vida cuando este fenómeno de "emisión estimulada" fue propuesto. De hecho, la palabra láser es el acrónimo de la expresión en inglés Light Amplification by Stimulated Emission of Radiation, que en español podemos traducir como "amplificación de la luz por emisión estimulada de radiación".