III. DIFERENTES ENFOQUES PARA CONSEGUIR LA FUSIÓN NUCLEAR

SE HA mencionado en el capítulo anterior que sería totalmente inútil tratar de producir energía de fusión por medio de haces o rayos de núcleos acelerados, pues con ello se consumiría mucha más energía de la que se genera. Antes de describir los otros métodos que tienen la posibilidad de ser eficientes, delinearemos los argumentos que hacen descartar esta opción. Supongamos que uno de los grupos de núcleos se encuentra estático dentro de un gran recipiente de longitud L, y el otro grupo forma un haz acelerado que lanzamos hacia el interior de dicho recipiente. Al moverse los núcleos del segundo grupo a través del primero irán encontrando a su paso núcleos con los que pueden o no llegar a fusionarse, dependiendo de la distancia a que se encuentren al darse la interacción. Como hemos visto, la probabilidad de que ocurra la fusión está representada por la sección eficaz, de modo que si ésta es pequeña el núcleo tendrá que recorrer una gran distancia dentro del recipiente para llegar a encontrar otro núcleo con el cual se pueda dar una fusión. Por supuesto que cuanto mayor sea la densidad de núcleos estáticos habrá más probabilidad de que se dé el encuentro y que éste resulte en una fusión. Entonces, la distancia que tiene que recorrer una partícula, en promedio, para poder llegar a reaccionar (llamada comúnmente camino libre medio) es inversamente proporcional a la sección eficaz, a, y a la densidad de partículas: L_clm = 1/ (ns). Resulta que, para el valor máximo de s (en la reacción D-T) y una densidad típica de 10 ¹⁴ partículas por cm³, el valor mínimo de L_clm es 20 000 km. Lo que esto quiere decir es que para que haya suficiente producción de energía por las partículas aceleradas, la longitud del recipiente debe ser mayor o igual a 20 000 km, esto es, semejante al diámetro de la Tierra. Por supuesto será muy difícil construir un aparato de estas proporciones.

Se podría pensar que si se usa una densidad de partículas bastante mayor se podría reducir considerablemente el tamaño del recipiente, pero entonces otro problema empieza a ser importante: los efectos de colisiones atómicas y coulombianas (o sea, debidas a los campos eléctricos o de Coulomb). Aunque estas colisiones dan lugar a cambios de energía muchísimo menores que las producidas en un evento de fusión, son también mucho más frecuentes porque su sección eficaz es muy grande. Por tanto estas interacciones hacen que las partículas aceleradas vayan perdiendo energía en distancias relativamente cortas, especialmente si la densidad de las partículas estáticas es elevada. Con esto ya no habría energía suficiente para producir la fusión.

La impracticabilidad de este método también puede ser entendida en términos del criterio de emparejamiento descrito anteriormente y de acuerdo con el cual el valor mínimo que debe tener el parámetro n-t_E es del orden de 10 ¹⁴ s/cm³, de modo que si la densidad es 10 ¹⁴ partículas/ cm³ entonces el haz debe de permanecer dentro del recipiente durante 1 segundo. Como la energía cinética de los núcleos debe ser de 100 keV, la velocidad es 3 X 10⁸ cm/ s y la distancia recorrida en 1 segundo tiene que ser d = vñt = 3 000 km. Otra vez fuera de proporción con las dimensiones de un reactor.

Con esto queda claro que debe pensarse en mecanismos alternos que generen energía por fusión de manera eficiente. En el capítulo anterior ya se habló de que existen enfoques fríos y calientes. El uso de estos términos es relativo ya que al referirse al frío se piensa en gases a la temperatura ambiente, pero lleva ese nombre en contraste con los métodos calientes donde las temperaturas alcanzan varias decenas de millones de grados. En ambos casos se trata de mantener un gas confinado en una región, de forma que el criterio de emparejamiento se satisfaga. El gas debe estar ya compuesto de las dos especies reactantes (o una sola en caso de ser reacciones D-D o T-T las que se deseen) y se debe buscar iniciar el proceso de fusión, lo que ocurre de distinta manera en las dos alternativas.

Describiremos primero los enfoques calientes, en primer lugar porque fueron los primeros en utilizarse y en segundo porque son los más desarrollados. Ya se sabía desde el primer tercio de este siglo que la fusión es la fuente de energía del Sol, pero el primer ejemplo concreto que se tuvo de que esta fuente, capaz de producir grandes cantidades de energía, puede de verdad estar a nuestro alcance fue, lamentablemente, como en muchos otros casos, en el ramo militar: la aparición de la bomba de hidrógeno o bomba H. Para obtener una gran cantidad de reacciones de fusión en un tiempo muy corto y que la energía se libere de manera explosiva, lo que se hace es comprimir un gas de deuterio (hidrógeno pesado) encerrado en una cavidad produciendo una implosión (lo opuesto a una explosión). Con esto se transmite gran cantidad de energía a los núcleos de deuterio y se obtienen temperaturas extremadamente altas, de modo que es posible traspasar la barrera de Coulomb y producir la fusión. En el caso de la bomba H, esto se logra mediante la detonación previa de otra bomba, una bomba atómica (o sea de fisión nuclear). La energía impartida por ésta es suficiente para que los átomos (o núcleos) de deuterio produzcan reacciones de fusión en número bastante elevado. Cuando las temperaturas son muy altas no se tiene el problema de las colisiones atómicas y coulombianas mencionado anteriormente porque su sección eficaz decrece al aumentar la velocidad (proporcional a la temperatura). En este proceso las densidades son relativamente grandes, lo que aumenta la eficiencia.

Las bombas mostraron que es posible tener energía de fusión, pero esta energía no puede ser aprovechada con fines pacíficos ya que se produce sin control alguno. La finalidad de la investigación actual sobre la fusión es lograr un mecanismo que la controle, de manera que pueda ser utilizada a voluntad. En este caso la idea sigue siendo calentar un gas hasta temperaturas muy altas, pero manteniendo el control del número de reacciones de fusión. A esta aproximación a la fusión se le llama fusión termonuclear, ya que se aprovecha el movimiento térmico de las partículas para que las colisiones entre ellas den lugar a la fusión. El gran objetivo de muchos científicos es lograr la fusión termonuclear controlada.

Cuando se eleva la temperatura de un gas a valores muy altos las partículas del gas, que normalmente son eléctricamente neutras (formando átomos o moléculas), dejan de serlo, pues los fuertes choques entre partículas hacen que los electrones se desliguen de sus núcleos. A este proceso de pérdida de electrones se le llama ionización y al átomo con déficit de electrones, ion. El nombre que dan los físicos al gas ionizado es plasma. Este en conjunto es por lo general eléctricamente neutro, pero debido a que contiene dos especies de partículas cargadas su comportamiento es muy diferente y más complejo que el de un gas sin ionizar. El estudio del plasma es fundamental para la investigación sobre la fusión termonuclear, y por ello el desarrollo de estas dos disciplinas ha ido de la mano durante los últimos 30 años. Antes de que comenzara el gran interés por la fusión el conocimiento de los plasmas era muy limitado, habiéndose estudiado sólo en relación a problemas de física espacial y tubos de descargas eléctricas.

Tanto en los gases no ionizados como en los plasmas, las partículas componentes se mueven continuamente, con velocidades muy variadas. Si uno pudiera contar cuántas partículas se mueven con una velocidad dada y se graficaran estos números para todas las velocidades se obtendría una curva como la de la figura 4, que muestra la distribución de velocidades para un gas en equilibrio térmico. A esta distribución se le llama función de distribución de Maxwell o simplemente maxwelliana, y resulta ser la función que obedece cualquier sistema que ha llegado a evolucionar libremente hasta alcanzar un estado de equilibrio (donde ya no cambia con el tiempo). La característica es que presenta un pico que indica que gran parte de las partículas se mueven con velocidades muy parecidas, alrededor de la llamada velocidad térmica, vt. Su posición y anchura dependen de la temperatura del gas. Sin embargo, hay que hacer notar que también existen partículas con velocidades muy altas en la cola de la distribución. Aunque en bajo número, su presencia es importante en la fusión.

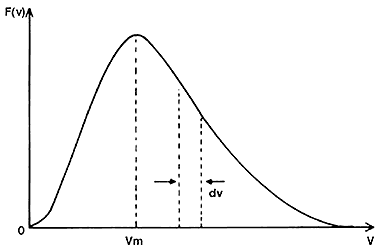
FIGURA 4. Función de distribución de velocidades maxwelliana para los átomos (o moléculas) de gas en equilibrio térmico. La velocidad térmica v_t es la que tiene la mayoría de los átomos, y es casi igual a la velocidad del máximo de la distribución vm.

La probabilidad de fusión para un plasma maxwelliano tiene que ser obtenida considerando todas las partículas, así que hay que promediar la sección eficaz (que nos mide la probabilidad para una velocidad dada) sobre una distribución maxwelliana. En realidad el promedio que más interesa es el del producto de la sección eficaz s por la velocidad de las partículas v, que denotamos por <sv>, pues esto mide la probabilidad de reacción por unidad de tiempo. En la figura 5 se muestra esta cantidad en función de la temperatura de la maxwelliana utilizada en el promedio, para las mismas reacciones consideradas previamente. En el caso de la temperatura se emplean unidades de energía en lugar de grados pues hacerlo da una mejor idea del nivel de agitación que tienen las partículas que componen el plasma⁶ y además permite compararla con las energías de las partículas individuales. Comparando esta gráfica con la de la figura 3 se nota que el pico en la probabilidad de reacción ocurre a temperaturas mucho menores que las energías del pico de la sección eficaz; por ejemplo, para D-T se tiene 60 keV contra 120 keV, respectivamente. Se observa también que la probabilidad de reacción para D-T es todavía razonable a temperaturas de 20 keV. Esto es un reflejo de la presencia de las partículas de la cola de la distribución maxwelliana y muestra la ventaja de usar un plasma en lugar de haces de partículas energéticas.

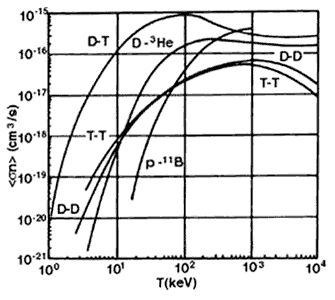
Figura 5. Tasa de reacción s para las principales reacciones de fusión, como la temperatura del gas.

La potencia de fusión generada en un plasma termonuclear será proporcional al número promedio de reacciones por unidad de tiempo (determinado por la probabilidad de reacción y la densidad de las partículas reactantes) y a la energía liberada por la reacción. Según el combustible utilizado, la potencia será mayor o menor; otra vez, la máxima potencia se alcanza con la mezcla D-T, ya que la probabilidad de fusión y la energía generada son grandes en relación a otras reacciones. Parte de esta potencia será utilizada para mantener al plasma caliente, y generalmente es la que llevan las partículas alfa, ya que son las más fáciles de controlar. La potencia restante puede ser utilizada para generar electricidad.

El criterio de emparejamiento referido con anterioridad puede ser formulado en términos más específicos para un plasma termonuclear. Es necesario señalar que las altas temperaturas requeridas en el plasma hacen que toda esta energía térmica no pueda ser contenida más que por un tiempo finito, al que se llama tiempo de confinamiento de energía, t_E. En términos de t_E se puede establecer la condición para que la ganancia de energía se empareje con las pérdidas. La energía perdida viene de la energía térmica que se escapa y de la radiación electromagnética emitida, mientras que la única fuente de energía es la que se genera por fusión. Si toda la energía que llega a la pared del aparato (la perdida más la generada) es captada y se convierte en energía útil con una eficiencia e, el resultado de este proceso tendrá que ser mayor o igual que la energía que hay que suministrar al plasma para mantenerlo activo, a fin de que las pérdidas no dominen a las ganancias. Esta condición puede expresarse como,

	3T
n tE³
	[PF ( e/1 -e ) - PR] / n2

donde P_F y P_R son las potencias de fusión y radiación, respectivamente, y T la temperatura en unidades de energía. El lado derecho de esta relación depende sólo de la temperatura, para una eficiencia dada. A esta condición se le llama criterio de Lawson, que fue quien primero estableció las condiciones de equilibrio de pérdidas y ganancias.

Otro concepto que se maneja con frecuencia en relación a los balances de energía es el de ignición o encendido de un plasma. Se dice que un plasma termonuclear ha alcanzado el estado de encendido cuando la energía de fusión producida (o parte de ella) puede ser reabsorbida manteniendo la temperatura constante. El plasma habrá llegado entonces a una situación autosostenida, donde ya no es necesario que se suministre energía del exterior. La condición de encendido es más fuerte que el criterio de Lawson para el emparejamiento de pérdidas y ganancias. Si se supone que las partículas alfa son las únicas que pueden quedar dentro del plasma y darle su energía, con potencia Pa, el criterio de encendido es,

	3T
n tE3
	[Pa - P8] / n2

En la figura 6 se muestran los dos criterios en función de la temperatura, para la reacción deuterio-tritio. El régimen de operación de un reactor termonuclear debe quedar arriba de estas curvas; o sea, T en el rango 10-20 keV, y nñt_E del orden de 10 ¹⁴ seg/cm³ o mayor.

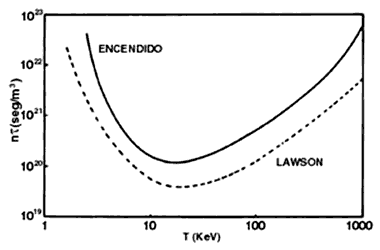
FIGURA 6. Valores del producto de la densidad del plasma n por el tiempo que permanece confinada su energía t, necesarios para el emparejamiento de pérdidas y ganancias (criterio de Lawson) y para el encendido, ambos en función de la temperatura del plasma.

Para satisfacer estos requerimientos se puede escoger entre, tiempos de confinamiento de energía pequeños pero densidades grandes, o tiempos de confinamiento largos a densidades moderadas. En el primer caso se obtienen plasmas muy calientes confinados por su propia masa, por lo que se llama confinamiento inercial. En el segundo caso, para mantener al plasma confinado por "mucho" tiempo se emplean campos magnéticos, pues éstos actúan sobre las partículas cargadas que forman el plasma; éste es el confinamiento magnético. Ambos enfoques serán tratados con detenimiento en capítulos subsecuentes por lo que aquí nos limitaremos a mencionar las ideas básicas de cada uno ellos.

En el confinamiento inercial se usa un mecanismo similar al que opera en una bomba de hidrógeno pero a microescala. La idea es formar pequeñas pelotillas de combustible fusionable (D, o D-T) e irradiarlas uniformemente con alguna fuente de energía desde el exterior para calentarlas. Al comprimirse el material de la pelotilla, alcanzará temperaturas muy altas en su centro por un tiempo muy corto; del orden del tiempo de confinamiento inercial. Este tiempo está determinado por la tendencia a expanderse libremente de un gas que no está encerrado, pues es la expansión la que termina con el confinamiento. Lo único que detiene o retarda la expansión es la masa de las partículas del gas ya que si no tuvieran masa se expandería instantáneamente; de ahí el nombre inercial.⁷ La velocidad de expansión es del orden de la velocidad del sonido en el gas, v_s, pues ésta es la velocidad a la que se propaga una perturbación de presión en ese medio. Por esta razón el tiempo de confinamiento ti= R/ v_s en una pelotilla de radio R disminuye al aumentar la temperatura (dado que v, ~ ñT).

Los tiempos de confinamiento típicos de este esquema son del orden de picosegundos (billonésimos de segundo) y las densidades entre 10 ²⁵ y 10 ²⁶ partículas por cm³. Los diámetros de las pelotillas que se usan son de centenas de micras. Para poder concentrar la gran cantidad de energía necesaria sobre blancos tan pequeños se necesita una concentración de energía muy elevada. Esto se ha estado tratando de lograr disparando hacía las pelotillas haces energéticos uniformemente distribuidos alrededor de ellas. Cuatro tipos de haces se han estado investigando: 1) láseres de alta potencia, 2) electrones relativistas, 3) iones pesados y 4) iones ligeros. Los experimentos más avanzados hasta la fecha son los realizados con láseres. Estos son fáciles de propagar y enfocar sobre el blanco, pero su eficiencia eléctrica es baja. En contraste, los haces de iones y electrones tienen eficiencias aceptables, pero es difícil enfocarlos sobre el blanco.

La combinación alternativa para satisfacer el requerimiento sobre el producto nñt_E (tiempos largos y densidades bajas) tiene otras limitaciones. Si la densidad es demasiado baja la potencia producida sería muy pequeña y se necesitarían volúmenes enormes, difícilmente realizables, para producir las potencias eléctricas deseadas (10 ⁹ watts). Además, no es posible lograr tiempos de confinamiento muy grandes debido a que los plasmas termonucleares no están generalmente en equilibrio térmico, por lo que son, en el mejor de los casos, ligeramente inestables. Las inestabilidades internas dan lugar a lo que se llama transporte anómalo, lo que origina pérdidas de energía rápidas, y limita el tiempo de confinamiento. Estas y otras consideraciones, tales como la carga de potencia máxima que pueden soportar las paredes del aparato (lo cual pone un límite superior a la densidad), llevan a considerar valores de t_Eñ1 segundo y n=10¹⁴ a 10¹⁵ partículas por cm³. Con esto uno se puede dar una idea de lo que quiere decir tiempos largos en fusión. Con respecto a las densidades, se puede comparar con la densidad del aire a temperatura ambiente, que es de 10 ¹⁹ partículas/cm³; o sea que en este caso se emplean valores unas cien mil veces menores, mientras que en confinamiento inercial se requieren densidades un millón de veces mayores que la del aire.

Para conseguir estos parámetros se debe encerrar el plasma en algún recipiente hermético, pues en relación al exterior las condiciones son casi como del vacío. Sin embargo, hay que evitar en la mayor medida posible que entre en contacto con las paredes del recipiente, pues alcanza una temperatura altísima y la interacción con la pared lo enfriaría y contaminaría fuertemente con el material de ésta, además de que puede llegar a fundirla. Por esta razón es necesario confinar el plasma mediante campos magnéticos, los cuales constriñen el movimiento de las partículas cargadas, limitando así el volumen que ocupa. Se puede tener una idea de la magnitud de los campos magnéticos requeridos, si se reconoce que un campo magnético ejerce presiones sobre la materia de la misma forma que lo hace un fluido. Esta presión magnética depende del cuadrado del tamaño del campo y un campo magnético de 1 Tesla ⁸ equivale a tener tres atmósferas de presión. Ahora, para un plasma de densidad 10¹⁴ partículas/cm³ y temperatura de 10 keV la presión, p = nñT, es de 2 atmósferas. El tamaño relativo de estas presiones se mide a través de un parámetro llamado beta (b),

	nT
b =
	B2 / (8p)

donde B es la magnitud del campo magnético. Para que el campo magnético pueda dominar al plasma, b debe ser menor que uno por lo que el mínimo valor de B es algo menor que 1 Tesla. Sin embargo, existen problemas de estabilidad del plasma cuando b es del orden de uno, por lo que los esquemas de confinamiento actuales consideran betas de entre 0.05 y 0.1 en un reactor. Esto requiere de campos magnéticos de 2 a 5 Teslas que son muy difíciles de conseguir y sólo pueden mantenerse por tiempos cortos, a menos que se usen bobinas superconductoras.

Los diseños de reactores de fusión basados en el confinamiento magnético y que toman en cuenta las limitaciones tecnológicas mencionadas arriba consideran potencias de operación en la vecindad de 100 watts/ cm³. Por lo tanto, para tener una planta eléctrica de 1 000 Mwatts, el reactor necesitaría tener un volumen de 300 m³, si la eficiencia de conversión de energía térmica a eléctrica se toma de 30%. Se puede notar entonces que se necesitan plasmas termonucleares muy grandes para este esquema. El confinamiento magnético es el que más ha sido desarrollado durante las tres últimas décadas y por ello es el que tiene mayores posibilidades de éxito.

Nos resta solamente mencionar en qué consiste el enfoque frío a la fusión nuclear. La idea fue sugerida hace más de 40 años pero sólo recientemente se ha empezado a considerar como una alternativa viable. En lugar de hacer chocar núcleos aislados para vencer la barrera de Coulomb se trata de acercarlos formando una molécula especial en la que la separación internuclear es muy pequeña. Cuando están muy juntos por un tiempo largo es bastante probable que se pueda traspasar la barrera de Coulomb debido al efecto túnel o de penetración de barrera (ver el capítulo IX). Así pues, en lugar de aumentar la energía de los núcleos a valores muy grandes, como en la fusión termonuclear, se trata de mantenerlos muy cercanos hasta que se dé la penetración de barrera. El punto clave es cómo se forma una molécula "compacta", con los núcleos muy juntos.

A reserva de que se explique mejor el mecanismo de la fusión fría en un capítulo posterior, mencionaremos aquí que para lograr el objetivo anterior se utiliza un tipo de partículas elementales llamadas mesones mu (m) negativos o simplemente muones. Estas partículas toman el lugar del electrón en una molécula normal, pero como su masa es 200 veces mayor que la del electrón, su órbita es más cerrada lo que a su vez hace que los núcleos queden 200 veces más cerca. El muon actúa entonces como catalizador para que se pueda llegar a tener la fusión de los núcleos de la "muomolécula". La energía liberada en la reacción es llevada en su mayor parte por el muon, que queda libre, y podría, en principio, formar otra molécula para catalizar otra reacción. El principal inconveniente de este proceso es que el tiempo de vida de un muon es muy corto (dos millonésimas de segundo) y decae antes de poder catalizar más reacciones, lo cual hace que no sea muy eficiente, pues se necesitaría que la energía liberada por las fusiones catalizadas por un muon fuera mayor que la invertida en crearlo. Por ello no se había considerado como alternativa para generar energía. Empero, en los últimos años ha habido avances teóricos y experimentales en relación a la fusión catalizada por muones, que muestran que la eficiencia se puede mejorar considerablemente, lo que ha traído nuevas esperanzas para este tipo de fusión.