II. QUÉ ES LA FUSIÓN NUCLEAR

COMO su nombre lo indica, la fusión nuclear es un proceso de unión (fusión) de dos núcleos atómicos para formar uno solo. ¿Qué tiene de interesante juntar dos cuerpos y dejarlos unidos? Eso lo hacemos, por ejemplo, al modelar con barro o plastilina sin que a nadie le cause asombro. Lo que hace peculiar la fusión de dos núcleos es la naturaleza de las fuerzas que mantienen unidos sus componentes, los protones y los neutrones, a los que genéricamente se les llama nucleones. Resulta que la fuerza nuclear tiene la particularidad de ser muy intensa pero de muy corto alcance, es decir, solamente cuando dos nucleones se encuentran muy próximos sienten la atracción mutua, en cuyo caso esta fuerza domina completamente cualquier otra fuerza presente (como la repulsión eléctrica entre protones).

Cuando un nucleón está rodeado de otros nucleones siente una fuerza neta que es la suma de las fuerzas ejercidas por cada nucleón por separado y si quisiéramos arrancar este componente del núcleo necesitaríamos darle una energía suficiente para vencer esta fuerza neta. A la energía mínima necesaria para hacerlo se le llama energía de enlace. Al aumentar el tamaño del núcleo (o sea, el número de nucleones) la energía de enlace va creciendo debido a que hay más nucleones ejerciendo atracción, pero debido al corto alcance de la fuerza sólo los nucleones más cercanos contribuirán de manera significativa. Por esta razón, el aumento en la energía de enlace es muy pronunciado cuando se empieza a aumentar de tamaño un núcleo pequeño y, a medida que se siguen agregando partículas, su efecto es cada vez menor porque están más distantes, lo cual hace que la energía de enlace casi no aumente. Así se tiene que para todos los núcleos más pesados la energía de enlace de un nucleón es prácticamente la misma y son más difíciles de romper que los ligeros.

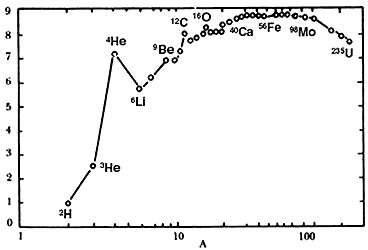
Figura 1. Energía de enlace por nucleón en función del número de nucleones A (protones y neutrones) que forman un núcleo, para todos los elementos naturales. Nótese la máxima energía de enlace alrededor del hierro Fe.

La situación que se acaba de describir se ilustra en la figura 1, donde se muestra la variación de la energía de enlace promedio que tiene cada nucleón (eje vertical) en función del número de masa A, es decir el número de nucleones (eje horizontal). Se puede apreciar que para elementos más ligeros que el hierro (Fe) el enlace aumenta en la forma descrita, alcanzando un valor aproximadamente constante del orden de 8MeV². Sin embargo, cuando el número de nucleones es ya muy grande, la energía de enlace disminuye lentamente otra vez. El hierro es el elemento en el cual la energía por nucleón es la máxima y, por tanto, es el más estable de todos. Aunque para entender la fusión nuclear no nos interesa lo que ocurre con los núcleos pesados, daremos una explicación del decrecimiento observado a fin de no dejar incómodas algunas mentes. Debido a que la fuerza nuclear de corto alcance ya casi no se siente entre los nucleones más alejados en un núcleo pesado, el efecto de la fuerza eléctrica se empieza a hacer sentir pues, aunque es mucho más débil, es de muy largo alcance. La fuerza eléctrica o de Coulomb es repulsiva por tratarse de partículas con carga del mismo signo³ y por lo tanto se opone a la fuerza nuclear, disminuyendo así ligeramente la energía de enlace. Cuanto mayor sea el número de protones mayor será la fuerza de Coulomb, lo que explica la disminución de la energía de enlace al aumentar la masa nuclear.

Al analizar la gráfica nos damos cuenta de que si tomamos dos núcleos que estén del lado izquierdo del máximo y los unimos para formar un nuevo núcleo más pesado, este último tendrá una mayor energía de enlace total (o sea, el resultado de multiplicar la energía de enlace de cada nucleón por el número de nucleones en ese núcleo) que la suma de los dos originales. Por tanto será más estable y permanecerá unido. El exceso de energía se presenta como energía cinética o de movimiento del nuevo núcleo, y como energía interna que puede hacer que se desprenda un nucleón. De esta manera se puede obtener energía aprovechable al fusionar dos núcleos ligeros en uno más pesado. La cantidad de energía liberada es del orden de la energía de enlace de los nucleones, que como ya se mencionó es de unos cuantos MeV, un millón de veces mayor que la liberada en las reacciones químicas (como la combustión del carbón). De ahí la gran importancia de las reacciones nucleares como fuente de energía.

Vale la pena mencionar que del lado derecho del máximo de la curva ocurre un fenómeno parecido, excepto que ahora se empieza con un núcleo pesado (por ejemplo el de uranio) y se divide en dos núcleos menos pesados, obteniendo como resultado una ganancia neta de energía. Este es el proceso de fisión nuclear, con base en el cual trabajan los reactores nucleares actuales.

El mecanismo de liberación de energía en una reacción de fusión nuclear puede ser también entendido desde un punto de vista distinto pero relacionado al anterior. Experimentalmente se ha medido que las masas de los núcleos atómicos no aumentan de manera uniforme conforme se avanza en la Tabla Periódica de los Elementos. Por ejemplo, la masa de un núcleo de helio, que está formado por dos protones y dos neutrones, es menor que si se sumaran las masas individuales de los dos protones y los dos neutrones; igualmente, resulta menor que la suma de las masas de dos núcleos de deuterio (un isótopo⁴ del hidrógeno que tiene un protón y un neutrón). El ingrediente adicional que se necesita en la explicación es la famosa equivalencia de masa y energía que encontró Einstein en la teoría de la relatividad: E = mc². Una pequeña masa equivale a una cantidad muy grande de energía dado que la velocidad de la luz es enorme: c² = 9 X 10 ¹⁶ m²/ s². La diferencia de las masas se debe a que se ha empleado parte de ellas en la energía para unir a los nucleones. Podemos entonces entender que al unir dos núcleos ligeros (como el deuterio) y formar uno más pesado (como el helio) la masa final será menor que la inicial y la diferencia tendrá que ser liberada como energía. Esta será una cantidad grande de energía, aun cuando la diferencia de masas es pequeña.

Una vez entendida la razón por la cual se puede obtener energía por fusión nuclear, hay que ver de qué manera puede lograrse esta fusión y qué tan fácil es hacerlo. Es aquí donde empiezan las dificultades prácticas debido a que todos los núcleos están cargados eléctricamente con signo positivo. Para poder unir dos núcleos hay que vencer la fuerza de repulsión que ejercen entre sí, para lo cual debe invertirse bastante energía. Este problema no se tiene en el caso de la fisión nuclear puesto que solamente se tiene un núcleo que se va a dividir y esto se logra agregándole un neutrón (que no tiene carga eléctrica) para desestabilizarlo.

Podemos explicar la problemática de las reacciones nucleares por medio de una gráfica de la energía potencial como la de la figura 2. Ahí se muestra la energía potencial en función de la separación, r, entre dos núcleos y lo que esto representa es la energía que necesita tener un núcleo cuando está muy separado del otro (teóricamente en infinito), para poder llegar a una distancia de separación dada por r. Para distancias mucho mayores que el radio nuclear la fuerza repulsiva de Coulomb es la única de importancia, la cual da lugar a una energía potencial que decrece como el recíproco de la separacion: E_c= constante/ r. Cuando los dos núcleos están muy juntos la interacción dominante es debida a la fuerza nuclear atractiva, cuya energía potencial no tiene una dependencia simple con la distancia pero es de signo contrario a la de Coulomb. Cuando se suman las dos contribuciones se forma una barrera de potencial, seguida de un pozo, a separaciones muy pequeñas. La gráfica puede interpretarse de manera sencilla si se piensa en ella como el relieve de un terreno sobre el cual rueda un objeto en presencia de gravedad. Al aproximarse dicho objeto por la derecha con cierta velocidad (o energía cinética), tiene que empezar a subir la cuesta y si su energía no es suficiente llegará a un punto en el que se detenga y empiece a regresar. Para poder llegar a la cima del potencial necesita de una energía inicial grande, en cuyo caso pasará por encima de la barrera y caerá al pozo, de donde no podrá ya salir fácilmente. Lo mismo ocurre con dos núcleos; la energía cinética o de movimiento que debe tener inicialmente uno con respecto al otro, que llamaremos E₀, debe ser mayor que la altura de la barrera de Coulomb a fin de poder llegar a sentir las fuerzas nucleares que los unirán, cayendo al pozo de potencial, cuya profundidad, -U_min, está determinada por la energía de enlace. Al ocurrir esto, el núcleo resultante tendrá una energía E₀ + U_min y se dice que está en estado excitado. El exceso de energía se emite a veces como radiación electromagnética (rayos g) u otras veces expulsando una partícula energética de su interior.

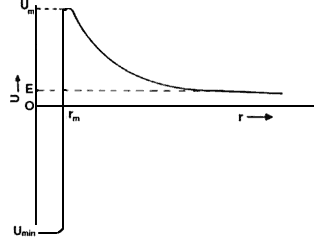
FIGURA 2. Variación de la energía potencial U entre dos núcleos, como función de la distancia de separación entre ellos. Puede interpretarse como el relieve de un terreno. A grandes distancias se repelen porque el declive empuja hacia r grande; pero si se logra pasar por encima de la colina en r_m los núcleos se atraen fuertemente.

En realidad, la situación no es exactamente como se acaba de describir, en el sentido de que no es absolutamente necesario que el núcleo tenga una energía inicial mayor que la altura de la barrera. Esto se debe a un efecto cuántico que se conoce como efecto túnel o de penetración de barrera. Sin entrar en detalle, mencionaremos que a escalas subatómicas las leyes clásicas de la física no son aplicables, siendo reemplazadas por la llamada mecánica cuántica, la cual no determina con certeza el resultado de un experimento; solamente puede dar la probabilidad de que ocurra un cierto evento. Como consecuencia, cuando una cantidad de partículas es lanzada hacia una barrera de potencial, con menor energía que el alto de la barrera, existe cierta probabilidad de que una fracción de ellas pase a través de ésta. Tomando en cuenta este efecto, no es necesario que para conseguir la fusión dos núcleos interactuantes lleguen a sobrepasar la altura de la barrera de Coulomb, que en el caso de dos deuterones asciende a 280 keV. Este hecho permite que las posibilidades de lograr la fusión nuclear se amplíen, ya que las energías requeridas pueden ser comparativamente bajas.

La manera más fácil e inmediata de obtener la fusión de dos núcleos es formando un haz de muchos de ellos por medio de un acelerador de partículas, con energía suficientemente alta como para traspasar la barrera de Coulomb, y hacerlo chocar contra un blanco formado también por núcleos del mismo tipo. Así, se tendrá que algunos de los núcleos llegarán a fusionarse. Con este mecanismo indudablemente se tendrá una liberación de energía nuclear pero será mucho menor que la energía que tuvo que invertirse en producir el haz. Este tipo de fusión tendrá valor únicamente como método para conocer los parámetros experimentales necesarios para lograr la reacción, pero nunca podrá usarse para producir energía neta. Uno de los parámetros que se obtienen con este tipo de experimentos es la sección eficaz o sección recta de colisión. Esta cantidad es muy usada cuando se producen choques entre dos partículas, y lo que mide es esencialmente la probabilidad de que, al encontrarse dos partículas, se tenga como resultado una fusión (aunque también se usa en otros procesos). Más específicamente, la sección eficaz representa el área que presenta el interior de un tubo imaginario centrado en una partícula y visto desde un extremo, de modo que, cuando otra partícula que se mueve a lo largo del tubo se encuentra dentro de él, se da la fusión pero no si está fuera. Este parámetro depende de la velocidad relativa de las partículas, que, si se mueven muy rápido, la distancia de acercamiento para conseguir la fusión será menor que cuando lo hacen lentamente.

Con el procedimiento mencionado se han podido medir las secciones eficaces de las diferentes reacciones de fusión entre núcleos ligeros. Así se conoce qué reacciones tienen mayor sección eficaz y por tanto son más adecuadas para obtener energía de fusión con mayor facilidad. La reacción más fácil de obtener viene de la interacción entre deuterio y tritio (el isótopo del hidrógeno con dos neutrones y un protón). Simbólicamente se escribe,

²D+ ³T® ⁴He (3.5 MeV)+ n(14.1Mev)

lo que significa que la unión de un núcleo de deuterio⁵ con uno de tritio resulta en un núcleo de helio-4 más un neutrón libre. Los números entre paréntesis indican la energía que adquiere cada una de las partículas como resultado de la fusión. Otra reacción importante que tiene una sección eficaz algo menor es la de dos deuterones, la cual puede tener dos resultados, cada uno con 50% de probabilidad:

²D+²D²®³HE (0.82 MEV) + N (2.25 MeV)

²D+²D®³T(1.0 MEV) + p (3.02 MeV)

En el primer caso se tiene helio-3 (el isótopo con un neutrón y dos protones) y un neutrón, mientras que en el segundo se produce tritio y un protón. Como se puede observar, estas reacciones producen menos energía que la anterior. Sin embargo son de gran importancia porque el deuterio ocurre de manera natural en una proporción de una parte en 6 500 de hidrógeno, de manera que en el agua es muy abundante y alcanzaría para satisfacer las necesidades energéticas del mundo por mil millones de años. La separación del deuterio del agua se hace con un proceso bien conocido y relativamente barato. En contraste, el tritio no existe de manera natural (decae en un tiempo medio de 12.3 años) y tiene que ser creado artificialmente, como por ejemplo al fusionar dos deuterones, según se muestra arriba.

Existen muchas otras reacciones, todas ellas con menores secciones eficaces, y para lograrlas se necesitan mayores velocidades de impacto. Algunas de las más frecuentemente citadas son,

²D+ ³He®⁴HE (3.67 MeV)+ p (14.68 MeV) ³T+³T®⁴He (1.26 MeV) + 2n (2x5.03 MeV) p + ¹¹B ® 3⁴He (3x2.89 MeV)

En la última se producen tres núcleos de helio-4 (llamados también particulas a), cada uno con 2.89 MeV de energía, al fusionarse un protón con un núcleo de boro. Una ventaja de esta reacción, al igual que de la primera de ellas, es que todos los productos son partículas cargadas y no se tiene neutrones. Esto es conveniente desde dos puntos de vista: 1) de las partículas cargadas se puede extraer su energía cinética desacelerándolas en campos eléctricos, lo que daría una fuente de energía eléctrica directa, sin necesidad de pasar por un ciclo térmico; 2) al no haber neutrones se elimina el problema de activación radiactiva de las paredes del reactor, y se incrementa la seguridad. En la figura 3 se muestran las secciones eficaces de las diferentes reacciones mencionadas como función de la energía cinética de los núcleos iniciales. Se puede apreciar que la reacción D-T es, con mucho, la más fácil de conseguir (nótese la escala logarítmica, o sea, en potencias de diez), sobre todo a bajas energías.

Aunque la reacción D-T produciría gran cantidad de neutrones muy energéticos que tendrían que ser atendidos de manera especial, se ha pensado en ella como la que será utilizada en la primera generación de reactores de fusión, ya que es la más accesible. A medida que la tecnología vaya mejorando y sea factible lograr las reacciones de secciones eficaces menores con relativa facilidad, se podrá pensar en emplear las que no producen neutrones, en ocasiones llamadas de combustibles avanzados. Por lo pronto, se ha pensado en obtener el tritio necesario para un reactor D-T, usando los mismos neutrones que resulten de la reacción D-T, a través de otra reacción dada por,

⁴Li+n®⁴He (2.1 MeV) + T (2.7 MeV)

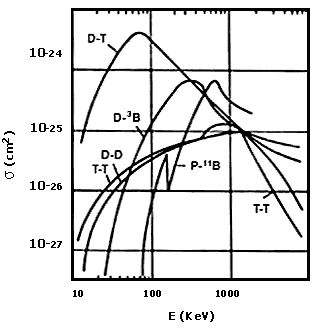
FIGURA 3. Sección eficaz s para la diferentes reacciones de fusión que se indican, en función de la energía cinética que tienen los dos núcleos antes de la reacción. La escala es logarítmica (en potencias de 10). La reacción más fácil de conseguir (la de menor o) es la de deuterio con tritio.

Para ello se rodearía al reactor de un cobertor de litio, que tendría la doble función de absorber neutrones y generar tritio, y además produciría energía adicional que se sumaría a la de la reacción D-T. De esta manera, el combustible primario sería el litio (además del deuterio), y sólo sería necesaria una cierta cantidad de tritio para iniciar la reacción. Un detalle adicional es que el litio natural está compuesto de dos isótopos ⁶Li y ⁷Li cuyas proporciones son 7.4% y 92.6%, respectivamente, por lo que es conveniente hacer uso del isótopo pesado por medio de la siguiente reacción endotérmica (o sea que absorbe en vez de generar energía), que sería inducida por los neutrones energéticos de la reacción D-T:

⁷Li+n®⁴He + He +3T+n-2.5 Mev

El neutrón liberado estaría entonces disponible para la reacción del ⁶Li. Cabe mencionar que hay evidencias de que las reservas de litio en nuestro planeta son lo bastante extensas como para no tener que preocuparse por su abasto.

Ahora bien, ¿cómo se puede producir energía por fusión con base en las reacciones descritas, de manera eficiente? A fin de producir mayor energía de la que se invierte es necesario asegurarse de que siempre haya una gran cantidad de núcleos que estén en condiciones de acercarse lo suficiente como para fusionarse casi simultáneamente. Esto sólo se puede lograr eficientemente si se encierra en cierta región un gas compuesto por los átomos requeridos (combustible) y se mantiene confinado bajo las condiciones necesarias para producir fusión, por un tiempo suficientemente largo. Las condiciones del confinamiento dependen del tipo de enfoque adoptado y se pueden dividir en frías y calientes. En el siguiente capítulo se describirán estas posibilidades con detenimiento. Lo que es importante mencionar aquí es que, a fin de que la energía producida por las reacciones en el gas pueda compensar las pérdidas que se produzcan y ser reutilizada para mantener las reacciones en marcha, es necesario que: 1) la densidad de partículas del gas no sea muy baja y 2) el tiempo medio para las pérdidas de energía no sea muy corto. Las condiciones que establecen qué tanto es densidad baja y tiempo corto se pueden expresar en términos de un criterio de emparejamiento (igualdad de pérdidas y ganancias). Lo que esto expresa es que el producto de la densidad, n, por el tiempo de confinamiento de la energía, t_E, debe ser mayor que una cierta cantidad que depende de la temperatura del gas, T, y de la eficiencia de conversión de energía de fusión a energía útil, E, así como del tipo de mecanismo usado para tener fusión,

n·t_E > factor (T, e)

Por ejemplo, en la fusión caliente de D-T el valor mínimo de este factor para una eficiencia E=O.4 es 4x10 ¹³ cm-3s, que ocurre a T=3 X 10 ⁸ °K. Con esto notamos que es importante poder tener bien confinado al gas reactante.

Para medir la producción de energía, a menudo se utiliza un parámetro Q, que representa la ganancia y se define como Q = (energía producida por fusión) / (energía total invertida). Para que la fusión pueda ser utilizable se requiere que Q sea mayor que uno. El criterio de emparejamiento se expresa en estos términos como Q = 1, y es la primera meta que se debe alcanzar.