V. EL USO DE CAMPOS MAGNÉTICOS PARA CONFINAR UN PLASMA

ES INDUDABLE que el confinamiento magnético es el más avanzado de todos y el que más posibilidades tiene actualmente de constituir la base de un reactor de fusión. Esto no es fortuito, ya que se le ha dedicado gran esfuerzo durante más de tres décadas, habiéndose experimentado con gran variedad de diseños e ideas. Pero antes de describir los diferentes aparatos experimentales analizaremos la capacidad del campo magnético como confinador de un plasma, al que con este fin lo consideraremos como una colección de partículas cargadas y veremos, primero, qué le sucede a una sola partícula al estar dentro de un campo magnético uniforme y homogéneo. La fuerza magnética, o fuerza de Lorentz, que siente una partícula con carga q se acostumbra a escribir en términos de vectores ¹¹ como F_L = q (v x B), donde la x indica producto vectorial, el cual da como resultado un vector (F_L) que es perpendicular a los dos vectores que se están multiplicando (el de la velocidad, v, y el del campo magnético, B). Consecuentemente, una partícula moviéndose en alguna dirección (que no sea la misma de B, porque entonces F_L es cero) será desviada continuamente hacia el mismo lado hasta llegar a la misma dirección inicial, completando así una órbita, que se va repitiendo. La magnitud de la velocidad no se altera. Si la proyección de la velocidad a lo largo de B (componente paralela) es cero, la partícula describe círculos alrededor de una línea de campo, pero si es distinta de cero, la órbita es una hélice que avanza a lo largo del campo magnético, como se observa en la figura 7. El signo de la carga determina en qué dirección es el giro.

El radio de la órbita (llamado radio de Larmor) se obtiene de igualar la fuerza de Lorentz a la fuerza centrípeta (la que mantiene a una partícula girando) obteniéndose, r_g = mvc / qB para una partícula de masa m, con velocidad v (c es la velocidad de la luz). Entonces los iones describen órbitas más grandes que los electrones, para una misma velocidad. Nótese que si la partícula está en reposo (v = 0), no siente ninguna fuerza y permanecerá así, pero en un plasma el movimiento térmico hace que todas las partículas sean afectadas. Tomando la velocidad más probable de una distribución maxwelliana de partículas (llamada velocidad térmica), se obtiene que los iones de hidrógeno de un plasma termonuclear en un campo de 10 kG (1 Tesla) tienen r_g= 1 cm, mientras que para los electrones vale un décimo de milímetro. Esto indica que los últimos se mueven casi únicamente a lo largo de las líneas de campo, cuando dichas líneas son rectas. Los radios de giro son muy pequeños en comparación con las dimensiones de los plasmas confinados para fusión.

De acuerdo a lo anterior, se puede pensar que la configuración más sencilla para confinar un plasma es un sistema de líneas de campo rectas dentro de una cámara cilíndrica. Las partículas sólo se pueden despegar de las líneas de campo una distancia de tamaño rg, así que no pueden llegar a las paredes de la cámara. Su movimiento es principalmente a lo largo del campo, de modo que el cilindro debe ser muy largo para que las partículas no se pierdan al llegar a los extremos. Para un cilindro de longitud L, el tiempo máximo que una partícula puede estar confinada es, t = L/v||, y si queremos que sea del orden de un segundo para una velocidad paralela v|| del orden de la velocidad térmica de los iones termonucleares, se necesitaría una longitud de 1 000 km. Puesto que un aparato de este tamaño es imposible de realizar, hay que buscar la manera de cerrar los extremos del cilindro. Como ya vimos, esto no lo podemos hacer con tapas materiales pues es perjudicial la interacción plasma-pared, así que se tiene que modificar el campo magnético en estas zonas para evitar el escape del plasma.

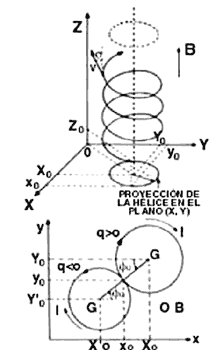
FIGURA 7. (a) Trayectoria en forma de hélice de una partícula cargada que se mueve en un campo magnético uniforme B. (b) La proyección de la trayectorai en un plano perpendicular al campo B es un círculo y la dirección depende del signo de la carga q.

El movimiento circular de una partícula cargada es semejante a tener una espira de corriente eléctrica diminuta, la cual genera un campo magnético en dirección perpendicular al círculo. Este campo resulta ser opuesto al campo original por lo que tiende a reducirlo ligeramente. Así, cada partícula que gira forma lo que se llama un dipolo magnético y es la suma de todos ellos la que disminuye el campo aplicado. En los casos en que el círculo tiene un radio demasiado pequeño para seguirlo en detalle, es más conveniente ver las partículas como dipolos diminutos que se mueven a lo largo de las líneas de campo, forzadas por el mismo campo magnético. La intensidad de un dipolo se mide por el momento magnético, m, de modo que para una densidad de dipolos o de partículas n, la reducción del campo magnético será B₁ = 4pnm. El momento magnético para el caso de una partícula girando aumenta al disminuir el campo magnético de acuerdo con la expresión: m = mv_^² / 2B, donde V_^ es la componente de la velocidad perpendicular al campo.

Una característica importante del momento magnético es que su valor se mantiene constante si el campo magnético varía lentamente. Además, como la energía cinética, y por tanto la magnitud de la velocidad de la partícula, se mantienen constantes, un incremento de la componente perpendicular debe ir acompañado de una disminución de la componente paralela y viceversa. Con esto en mente, uno podría aumentar la magnitud del campo magnético en los extremos del cilindro para cerrarlo. De esta manera, al acercarse una partícula a la región de campo intenso, su velocidad perpendicular aumenta a fin de mantener m constante, y consecuentemente la componente paralela disminuye. Si el campo es lo suficientemente intenso la velocidad paralela se anula en algún punto y la partícula empieza a moverse en sentido contrario, es decir se refleja y ya no escapa. Esta configuración funciona entonces como un espejo magnético, y al poner uno de ellos en cada extremo del cilindro se mantiene atrapadas a las partículas del plasma. Esto se muestra en la figura 8.

A pesar de la mejora que se tiene al colocar espejos magnéticos, el confinamiento es todavía incompleto. Por ejemplo, las partículas con velocidad perpendicular nula no giran y sólo se mueven a lo largo del campo sin sentir su efecto, así que no son reflejadas. En general, todas las partículas cuya velocidad paralela, en relación a su velocidad perpendicular, sea mayor que un cierto valor (que depende de qué tanto se incrementa el campo en los extremos), escaparán de la trampa magnética. Esto sólo se podría evitar si el campo magnético se hiciera infinito en los extremos. Aunque hasta ahora no se ha hecho caso de los choques entre partículas, si éstas se incluyen tendrán el efecto de ir cambiando la dirección de la velocidad, de modo que algunas partículas que inicialmente estaban bien atrapadas aumentarán su velocidad paralela y escaparán.

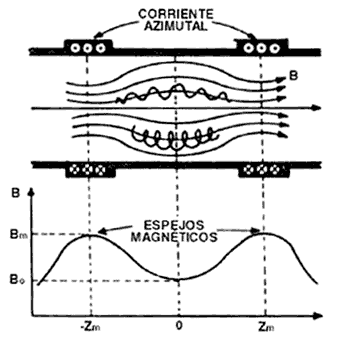
FIGURA 8. Configuración de un espejo magnético formada por dos bobinas separadas que llevan una corriente azimutal; el campo magnético es más intenso en esas zonas y las líneas de campo dejan de ser rectas. Las partículas cargadas quedan atrapadas entre los dos puntos de campo máximo.

Con los espejos magnéticos, las líneas de campo dejan de ser rectas, como se ve en la figura 8, pues de acuerdo a la representación de líneas, éstas se encuentran más juntas donde el campo es más intenso. Las líneas de campo curvas modifican el comportamiento del plasma, entre otras cosas, afectan su estabilidad. Así, la configuración de espejo no es estable cerca del centro de la trampa ya que el plasma, empujado por la fuerza centrífuga que resulta de moverse a lo largo de líneas curvas, puede "abrir" las líneas de campo y escapar. La inestabilidad que aparece es un caso particular de una clase de inestabilidades más general, llamadas gravitacionales. Una inestabilidad de este tipo, y de la cual toman su nombre, aparece cuando se pone un vaso de agua volteado boca abajo en presencia de la gravedad; un fluido denso (agua) es empujado hacia un fluido tenue (aire) por la fuerza de la gravedad. Como sabemos el agua cae porque es más estable la situación en la que el fluido denso se halla debajo del tenue. En nuestro caso se tiene algo equivalente donde la fuerza centrífuga reemplaza a la gravedad.

Para estabilizar la configuración sería necesario eliminar la curvatura o hacer que las líneas se curven hacia el lado opuesto. Se han propuesto varias maneras de lograrlo, entre ellas añadir cuatro barras (barras de Ioffe) al exterior del cilindro, con corrientes en direcciones alternantes, lo que produce que todas las líneas se curven hacia afuera. A esta configuración, mostrada en la figura 9, se le llama de "B mínimo" en vista de que B aumenta a lo largo de cualquier trayectoria que vaya hacia afuera del plasma. Modificaciones de esta configuración son las bobinas de beisbol (por la forma de la costura de estas pelotas), y las bobinas Ying-Yang (por un símbolo chino) que también se muestran en la figura 9. Posteriormente se tratarán mejores maneras de cerrar un espejo.

El problema de la pérdida de partículas por los extremos de un cilindro se puede resolver de manera alternativa: eliminando los extremos. En lugar de tener una configuración abierta se doblan las líneas de campo y se "une" un extremo con el otro, de modo que las líneas se convierten en anillos y el cilindro en un toroide (en forma de dona). En esta configuración, el campo está en la dirección llamada toroidal (la que circunda al hoyo de la dona), y la dirección perpendicular que rodea una sección menor del toroide se llama poloidal. Al tener una configuración cerrada, las partículas ya no pueden escapar a lo largo de las líneas de campo pero, siendo las líneas curvas, el movimiento se modifica de tal forma que pueden ahora moverse a través del campo. Este movimiento perpendicular a las líneas se denomina deriva, y se presenta siempre que haya una fuerza con una componente perpendicular a B.

El movimiento de deriva se puede entender si se analiza la órbita de una partícula en un plano normal a B (figura 10). En ausencia de fuerzas adicionales la única fuerza presente es la de Lorentz, que en todo momento apunta al centro del círculo, haciendo que la trayectoria de la partícula se curve siempre en la misma medida hasta formar un círculo. Ahora bien, al haber una fuerza con una componente sobre este plano, se suma vectorialmente ¹² con la de Lorentz de modo que, en los puntos donde éstas tienen la misma dirección, la fuerza deflectora se refuerza y la curvatura de la trayectoria es más pronunciada. En cambio, cuando son opuestas la fuerza total es más débil y las partículas se curvan muy poco. Esto da como resultado un desplazamiento neto en dirección perpendicular a la fuerza externa y al campo magnético, de modo que la trayectoria ya no es cerrada. Este movimiento se puede visualizar mejor si se le considera como la superposición de dos efectos: un movimiento circular alrededor de un centro (asociado a una línea de campo), y un movimiento con velocidad constante de este centro (llamado centro guía). La aproximación de centro guía es muy útil para estudiar los movimientos de las partículas en campos más complejos, pues sólo se analiza el movimiento del centro, olvidándose de las órbitas circulares. La velocidad del centro guía, o velocidad de deriva, hace que las partículas se desplacen a través de las líneas de campo magnético. Esta depende de la carga y tiene la forma v= c F x B/qB² para una fuerza F.

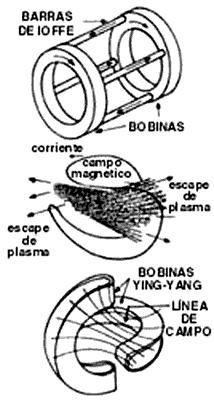
FIGURA 9. Diferentes configuraciones que se han ideado para mejorar la estabilidad de un espejo magnético, con las que se logra que B sea mínimo en el centro del plasma, evitando la curvatura cóncava hacia adentro de las líneas de campo.

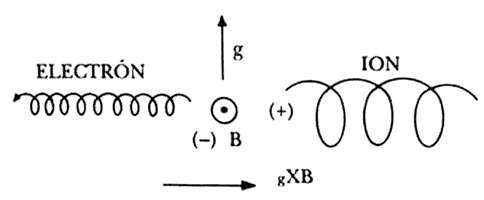
FIGURA 10. La velocidad de deriva producida por la acción conjunta del campo magnético B y una fuerza (gravitacional) g; la dirección es opuesta para cargas de distinto signo.

El caso en el que las líneas de campo son curvas puede ser analizado con el enfoque anterior ya que las partículas sienten una fuerza centrífuga, F_c, que es la que se combina con B para dar lugar a un movimiento perpendicular a B y F_c. En el caso de una configuración toroidal, se tiene además el efecto de que el campo magnético no es homogéneo, lo que produce otra deriva, parecida a la de curvatura. Estas derivas resultan ser verticales cuando el toroide está en posición horizontal, pero al ser dependientes de la carga, los iones y electrones se mueven en direcciones opuestas. Esto da lugar a una separación de carga, pues los iones se acumulan en la parte superior del toroide y los electrones en la parte inferior (o viceversa), y por lo tanto se produce un campo eléctrico vertical. Este campo, como actúa sobre las partículas con la fuerza eléctrica F_E = q E, va a dar lugar a otra deriva, pero esta vez la dependencia con la carga se cancela. El resultado es que todas las partículas, independientemente del signo de su carga, se mueven en la misma dirección, E x B, que es hacia el borde exterior del toroide. Con esto, todo el plasma en conjunto escapa del campo magnético y el confinamiento se pierde. El tiempo que tardaría en perderse el plasma es aproximadamente un microsegundo, por lo que no sería útil como sistema de confinamiento.

Para evitarle al plasma este destino fatal, debe buscarse la manera de que no haya separación de carga, pues así ya no habría campo eléctrico para producir la deriva. Puesto que la deriva de curvatura no puede eliminarse, la única manera de evitar que las cargas de signos opuestos se acumulen en los bordes superior e inferior, es hacer que cada línea de campo recorra el toroide por su parte superior y la inferior. Así, como las partículas siguen principalmente las líneas de campo, en su movimiento alrededor del toroide, parte del tiempo la pasan arriba y otra abajo, y no pueden acumularse en un lugar, a pesar del movimiento de deriva. Este comportamiento de las líneas de campo se puede ver gráficamente si una línea, en vez de formar simplemente un anillo, se enrosca sobre la dona a medida que le da vueltas en dirección toroidal; es como si se juntaran los dos extremos de un resorte. A esta forma de las líneas se le llama helicoidal (de hélice) y se puede lograr si se sobrepone un campo magnético poloidal al campo toroidal existente. El tamaño relativo de ambos campos determina qué tan enroscadas están las líneas, y para medir esto la gente que trabaja en este campo utiliza un parámetro al que llaman q. Una q grande quiere decir que las líneas se enroscan muy poco y el campo es casi puramente toroidal, mientras que si q es pequeña las líneas dan muchas vueltas en dirección poloidal antes de completar una vuelta en dirección toroidal. En general, q no debe ser ni muy pequeña, por razones de estabilidad, ni muy grande, porque tardaría tanto una partícula en ir de arriba a abajo que no se podría evitar la separación de carga.

Al seguir una línea de campo por muchas vueltas alrededor del eje del toroide se va cubriendo una superficie toroidal tubular. A estas superficies, donde están alojadas las líneas de campo, se les llama superficies magnéticas. Las superficies que pertenecen a diferentes líneas de campo están anidadas una dentro de otra y todas encierran al eje magnético. Este forma una circunferencia y puede pensarse en él como la superficie magnética más interna, que degenera en una línea. Cada superficie magnética puede ser identificada por la distancia al eje magnético, a la que se le llama radio menor. La inclinación de las líneas, medida por q, normalmente varía de una superficie a otra para evitar inestabilidades de gran escala. A esta variación de q con el radio menor se le conoce como cizallamiento. Los conceptos importantes de una configuración toroidal se muestran en la figura 11.

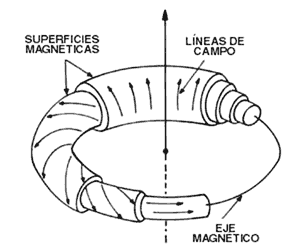
FIGURA 11. Configuración magnética toroidal que muestra las distintas superficies magnéticas (donde una línea magnética está alojada), que encierran al eje magnético. El cillazamiento es la variación de la dirección del campo magnético para diferentes superficies magnéticas.

Existen esencialmente dos conceptos para generar el campo magnético poloidal requerido: con corrientes fuera del plasma, o con corrientes dentro del plasma. Dentro de la primera categoría está la configuración conocida como stellarator, en la que se rodea la cámara de vacío toroidal con conductores helicoidales que llevan la corriente, que produce también líneas de campo helicoidales. En el segundo concepto se pueden separar los casos en que la corriente es llevada por el plasma mismo, de aquellos en que se introducen conductores ajenos al plasma. El primer caso está representado principalmente por el tokamak, en el cual se produce una corriente toroidal en el plasma para que se genere el campo poloidal, mientras que el campo toroidal es creado por bobinas externas independientes. El segundo enfoque se toma para los multipolos, que se forman con arreglos de aros conductores que llevan las corrientes, los cuales pueden mantenerse levitando, o con soportes a través del plasma. Además del tokamak hay muchas otras configuraciones que entran dentro de la misma categoría, como el esferomak, el compresor de campo invertido, etc., las cuales, al igual que el tokamak, el stellarator y los multipolos serán descritas en los dos capítulos siguientes.

Ahora examinaremos otros conceptos adicionales del comportamiento de un plasma en un campo magnético que pueden ser aplicados en configuraciones abiertas o cerradas. Consideraremos primero el movimiento de una partícula cargada en campos magnéticos heterogéneos, es decir que cambian con la posición, concentrándonos en el plano perpendicular al campo. Sabemos que, si el campo es uniforme, la partícula describe círculos cuyo radio depende de manera inversa a la magnitud del campo magnético. En la figura 12 se muestra el movimiento de iones y electrones cuando se tiene un campo que decrece en una dirección hasta hacerse nulo. Cada línea de campo se representa por un punto y el aumento en la intensidad del campo se muestra aumentando la densidad de puntos. Vemos que en la región donde el campo es más intenso el radio de giro es menor y avanza poco lateralmente, pero donde el campo es débil el gran radio de giro produce grandes desplazamientos. Como resultado hay una deriva del centro guía en dirección perpendicular al campo y a la dirección de variación de B, que va en sentidos contrarios para electrones e iones, similarmente a lo que se obtiene cuando hay una fuerza actuando. Nótese también que cuando una partícula que viene de la región sin campo se mueve hacia donde el campo aumenta, da una fracción de giro para así volver a la región de campo nulo, sin cambiar su energía. El campo magnético actúa entonces como una barrera que impide que las partículas lo penetren, lo que permite mantener al plasma contenido en un volumen dado. En este tipo de confinamiento el plasma debe ocupar una región en la que el campo magnético siempre aumente cuando nos movemos hacia afuera del plasma. Ya nos hemos encontrado una configuración de estas características anteriormente: la de B mínimo producida por los espejos de tipo beisbol o Ying-Yang. Podemos entender mejor ahora porque son mejores estos tipos de espejos magnéticos.

Existen otras configuraciones que usan este principio de B mínimo. Una es el multipolo mencionado antes, en el que las corrientes de los anillos se arreglan de forma tal que el campo poloidal presenta esta propiedad. Otra configuración importante es la del compresor theta, que consiste fundamentalmente de un cilindro con un campo magnético axial pero en el que la magnitud del campo es menor en el centro, donde está el plasma, que en la periferia. La particularidad de esta construcción es que el campo es generado por corrientes del plasma en su periferia, que fluyen en la dirección que va alrededor del cilindro, y no por bobinas. La coordenada que mide esta dirección es un ángulo al que se acostumbra llamar theta (q), y de ahí el nombre de esta configuración. Ligado a ésta también aparece el efecto de autocompresión que se describirá a continuación.

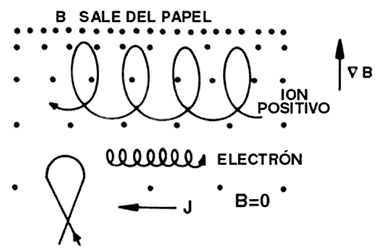
FIGURA 12. Movimiento de partículas cargadas en el plano perpendicular al campo magnético (representado por los puntos) cuando éste va disminuyendo hacia abajo hasta anularse. Se produce una deriva perpendicular a la dirección de variación del campo. Si la partícula viene de donde el campo es cero es reflejada de regreso.

Hasta ahora hemos aceptado que se puede describir al plasma como una colección de partículas individuales, sin interacción mutua, y solamente se ha analizado lo que le sucede a una partícula cualquiera. Alternativamente a esta descripción, se puede considerar al plasma como un fluido en donde lo que interesa es el comportamiento macroscópico de todas las partículas en conjunto. Al hacer esto ya se incorpora en cierta medida el efecto de la interacción de las partículas entre sí. Las ecuaciones que describen el comportamiento del plasma en presencia de un campo magnético desde este punto de vista, son las ecuaciones magnetohidrodinámicas (o MHD). Una de estas ecuaciones representa el balance de fuerzas, notablemente de la fuerza magnética (dada por j x B / c, donde j es la densidad de corriente en el plasma) y la fuerza de presión del plasma, que depende del cambio de la presión con la posición. Generalmente esta última es la que tiende a sacar al plasma de confinamiento pues da lugar a una expansión. La fuerza magnética debe de proporcionar el confinamiento oponiéndose a la de presión, por lo que hay que ajustar las corrientes y campos para este fin.

Consideremos ahora una situación en la que a un plasma cilíndrico se le hace pasar una corriente a lo largo de su eje, aplicándole una diferencia de potencial entre sus extremos. La corriente produce un campo magnético en dirección angular (o acimutal), y en el sentido de las manecillas del reloj, si lo miramos desde donde está fluyendo la corriente. Entonces, un elemento de plasma cualquiera sentirá la fuerza magnética debida a la interacción de la corriente j, con su propio campo B. Es fácil darse cuenta de que la dirección de esta fuerza apunta radialmente hacia el interior del cilindro, por lo que el plasma es comprimido y por lo tanto se calienta. El proceso continuará hasta que la fuerza de presión crezca lo suficiente como para compensar la fuerza magnética. A esto se le llama el efecto de autocompresión y, en principio, puede utilizarse para confinar y calentar un plasma. Este efecto puede también entenderse si se piensa que la corriente que pasa por el plasma consta de infinidad de filamentos de corrientes paralelas que, al sentir su atracción mutua (las corrientes paralelas se atraen y las antiparalelas se repelen), dan lugar a una compresión de la columna de plasma. A las configuraciones basadas en esta descripción se les llama compresores z o compresores lineales, ya que la corriente fluye a lo largo del eje del cilindro, al que se le asocia generalmente la coordenada z. El calentamiento de un compresor lineal sería producido por dos mecanismos: el calentamiento óhmico debido a la corriente, y la compresión de la columna, que si se da rápidamente, produce una onda de choque que calienta más eficientemente el plasma.

Un inconveniente de este mecanismo es que se requieren corrientes muy intensas para que se pueda dar el confinamiento a temperaturas y densidades termonucleares de manera efectiva; del orden de 1 MA (10⁶ amperes). En la práctica, estas corrientes tienen que generarse por medio de la descarga rápida de una gran cantidad de energía que se ha almacenado en un banco de condensadores, y por lo tanto no se pueden sostener por mucho tiempo. Aunque se ha estado investigando la generación de corriente por medio de radioondas, todavía no se alcanzan las magnitudes necesarias. Otro problema con las corrientes muy grandes es que el plasma no permanece en el centro del cilindro, sino que se vuelve inestable y se escapa hacia las paredes. Además, la presencia necesaria de electrodos en los extremos del cilindro produce pérdidas de calor adicionales. Por todas estas razones el compresor z no parece tener posibilidades como configuración de confinamiento para un plasma termonuclear, pero tiene interés histórico y ha sido la base para desarrollar diseños más adecuados que funcionan mucho mejor, como por ejemplo el tokamak.

Veamos en qué consiste la inestabilidad del compresor z y cómo puede remediarse. Supongamos que se ha alcanzado la situación de equilibrio MHD entre la presión del plasma, que empuja hacia afuera, y la fuerza de autocompresión, que empuja hacia adentro. Incidentalmente, este equilibrio también puede verse como el resultado del balance de presiones entre el exterior y el interior del plasma. En el exterior está la presión magnética y en el interior la presión de las partículas del plasma. En general, un estado de equilibrio se dice que es estable si al haber un pequeño desplazamiento de la posición de equilibrio, la reacción del sistema es tal que el equilibrio se recupera. Por ejemplo, una pelota en el fondo de una hondonada está en equilibrio estable porque si la empujamos en cualquier dirección tiende a regresar al fondo; en cambio si la pelota está en lo alto de una colina el equilibrio es inestable porque con cualquier desplazamiento empezará a rodar cuesta abajo. Regresando al equilibrio de nuestra columna de plasma, analicemos qué le pasa al ser perturbado. Hay muchos tipos de desplazamientos o perturbaciones que se pueden producir; los más sencillos son los que se muestran en la figura 13. El primero es un desplazamiento simétrico alrededor del eje del cilindro que estrangula la columna y el segundo es un desplazamiento lateral que tuerce la columna.

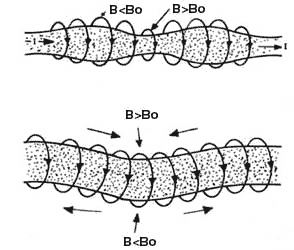
FIGURA 13. Inestabilidades de una columna cilíndrica de plasma que lleva una corriente eléctrica axial. Cuando es comprimida, el aumento del campo en esa región produce una mayor compresión hasta que se rompe. Al ser doblada, el campo aumenta en el borde interior de la columna y la hace doblarse aún más.

Para poder comprender qué le sucede al campo magnético con estas deformaciones, hay que mencionar dos propiedades de los campos magnéticos. Primero, cuando se tiene una corriente eléctrica recta, el campo magnético que se genera fuera del conductor (en este caso el plasma) es proporcional a la corriente total I y al inverso de la distancia desde el Centro de la corriente 1/r, de manera que a medida que nos alejamos, el campo magnético se vuelve más débil. El segundo es que, en las regiones donde el campo magnético es más intenso la densidad de líneas de campo es mayor (aunque éstas son sólo una representación del campo). Con esto en mente, veamos primero qué sucede al estrangularse la columna. Como en esta región tiene que seguir pasando la misma cantidad de corriente, el campo magnético justo en la frontera del plasma es mayor que antes de ser estrangulado, debido a que se redujo el radio. Con esto, la presión magnética aumenta y empuja hacia adentro al plasma, pues la presión del plasma no crece. La cantidad de plasma expulsada de esta región se va hacia donde el volumen es mayor y se empieza a hinchar. Resulta entonces que en la zona de estrangulamiento, la columna se vuelve cada vez más estrecha, mientras que a sus dos lados se va abultando, pues va encontrando presiones magnéticas cada vez menores. Consecuentemente, la perturbación es inestable. A ésta se le llama inestabilidad de salchicha, por la forma que desarrolla al haber varios estrangulamientos a lo largo de la columna.

En el segundo tipo de desplazamiento, cuando la columna se dobla, las líneas de campo quedan más juntas en la parte interna del doblez que en la externa. Así, el campo y la presión magnética son más intensos en el interior del doblez, ocasionando que éste se vuelva más pronunciado. Otra vez la situación lleva una inestabilidad, llamada de quiebre. Estas dos inestabilidades producen desplazamientos muy grandes que destruyen la columna de plasma rápidamente, por lo que son muy dañinas. Existe otro tipo de inestabilidades que afectan al plasma localmente, que no son tan perjudiciales, y son conocidas como microinestabilidades. Su efecto principal es sobre el transporte de energía y hablaremos de ellas posteriormente.

Ahora bien, nos podemos preguntar si hay alguna manera de evitar estas inestabilidades globales. Resulta que la respuesta es que sí, aunque se pierde la simplicidad del compresor z, pues hay que introducir un campo magnético adicional, lo que implica la presencia de bobinas. Para poder estabilizar la configuración basta con añadir un campo magnético axial (en la dirección z) de magnitud suficientemente grande. La razón por la que este campo mejora la estabilidad puede ser entendida si se piensa que las líneas de campo magnético se comportan como si fueran cuerdas tensas. Esta analogía es real, pues así como se le asocia una presión al campo también se puede calcular una tensión magnética que actúa a lo largo de las líneas de campo. Pensando en estos términos, cualquier deformación de la columna de plasma, ya sea de estrangulamiento o de quiebre, produce que las líneas de campo axial se curven, pero debido a la tensión, éstas tienden a regresar a su estado recto, lo que impide que la deformación crezca.

Para que el efecto estabilizador pueda tener lugar, la fuerza restauradora del campo axial debe ser la suficiente como para vencer las presiones magnéticas que deforman el plasma, es decir, el cociente del campo axial al campo acimutal debe ser mayor que un cierto valor. Recordando que el factor q constituye una medida de cuánto más grande es una componente del campo con respecto a la otra, la condición de estabilidad se reduce a: q > 1, en el borde del plasma. Con un compresor z modificado que satisfaga la condición anterior es posible tener buen confinamiento. Cabe mencionar que los conceptos del compresor z y el compresor theta, pueden ser usados tanto en sistemas de líneas abiertas como en sistemas cerrados. En el primer caso se ponen espejos en los extremos del cilindro para evitar la pérdida de partículas, mientras que en el segundo se forma un toroide. La idea del compresor z toroidal es la que da lugar al tokamak, que es el experimento más desarrollado hasta el momento. En el siguiente capítulo nos dedicaremos con detalle a este aparato.