XI. ¿QUÉ ES UNA ONDA?

ANTES de proseguir con nuestra narración revisaremos el concepto de onda, que será de mucha importancia.

Imaginemos una cuerda que está fija en uno de sus extremos a una pared (Figura 16) y que la sostenemos con la mano en su otro extremo. En el instante inicial la cuerda está en reposo y en posición horizontal. Ahora subamos la mano; al hacerlo moveremos la parte AB de la cuerda. En un instante posterior la porción BC de la cuerda empezará a subir. Posteriormente, CD empezará a subir y después, DE también lo hará, y así sucesivamente. De hecho, cuando la parte AB sube arrastra hacia arriba la porción BC; al subir BC arrastra a su vez hacia arriba a CD, etc. Es decir, al moverse cada parte de la cuerda arrastra la porción que está a su lado. En todo esto hay que darse cuenta de que nuestra mano solamente movió la porción AB; nuestra mano NO movió las porciones BC, CD, DE, etc. De hecho, ni siquiera las ha tocado.

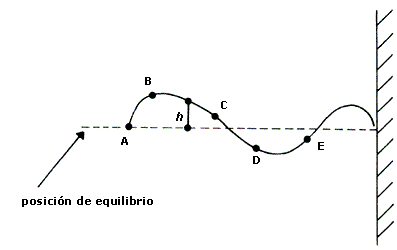
Figura 16. Al perturbar la cuerda en el punto A los demás puntos de la cuerda llegan a perturbarse. Esta perturbación es una onda.

Podemos decir que nuestra mano sacó a la cuerda de su posición de equilibrio, que es la horizontal; o sea, nuestra mano perturbó la cuerda, y más específicamente, la parte AB. A su vez, la parte AB perturbó la sección BC; en seguida, la parte BC perturbó la porción CD, etc. Es decir, la perturbación que nuestra mano causó en una parte bien precisa de la cuerda se ha ido propagando al resto de ella. Esta propagación de la perturbación es una onda. La perturbación que generó nuestra mano se propagó a lo largo de la cuerda. Se dice que la cuerda es el medio en el que se propaga la onda así generada.

En general, una onda es una perturbación que se propaga en un medio.

Otro ejemplo de creación de una onda ocurre cuando lanzamos una piedra a un estanque de agua. La piedra mueve el agua cuando toca su superficie. En instantes posteriores, partes adyacentes a la porción de agua en que cayó la piedra empiezan a moverse; nótese que estas partes no fueron tocadas por la piedra. Más tarde aún, otras partes del agua que tampoco fueron tocadas por la piedra empiezan también a moverse. La piedra causó una perturbación en el agua y esta perturbación se propagó. Es decir, se creó una onda. En este ejemplo la onda se propagó en el agua, o sea que el agua fue el medio.

Otro tipo de onda es el siguiente: consideremos un recipiente con aire en su interior; supongamos que la parte superior del recipiente está cubierta con una membrana elástica que no deja pasar el aire hacia afuera. Ahora apretemos la membrana para comprimir el aire dentro del recipiente. Para empezar, el aire adyacente a la membrana se comprime. Al transcurrir el tiempo esta región deja de estar comprimida, pero el aire que ocupa la región adyacente, dentro del recipiente, se comprime a su vez. De esta forma la compresión se va propagando a lo largo de todas las regiones del aire dentro del recipiente. Es decir, la perturbación que aplicamos al apretar la membrana, que comprimió el aire en la región AB, se fue propagando al resto del aire. Por tanto se generó una onda. En este caso la onda es de compresión del aire y el medio en que se propaga es precisamente el aire.

Otra posibilidad es que en lugar de apretar la membrana la estiremos hacia arriba. En este caso el aire que queda junto a la membrana ocupa un volumen mayor que el que tenía originalmente. Como las cantidades de aire son las mismas, ahora el aire queda diluido, es decir, rarificado. Este efecto es el opuesto al de compresión. Por lo tanto, al estirar la membrana la región adyacente a ella experimenta una rarefacción. En instantes posteriores las diversas regiones del gas se van rarificando. Es decir, la perturbación, que ahora es la rarefacción, se ha propagado en el aire. Es este caso, la onda así creada es de rarefacción.

También se puede generar una onda en que se propague tanto una compresión como una rarefacción. En efecto, supóngase que primero empujamos y luego jalamos la membrana. Al empujar comprimimos el aire y al jalar lo rarificamos. Lo que ocurre es lo siguiente: en primer lugar, la región adyacente a la membrana se comprime. Posteriormente, la región adyacente a la anterior se comprime. Si ahora la membrana se jala, entonces la región adyacente a la membrana se rarifica. Estas compresiones y rarefacciones se van propagando en el gas. De esta manera se ha generado una onda de compresión y de rarefacción. El sonido es justamente este tipo de onda.

Cuando hablamos emitimos sonidos. Nuestra garganta, a través de las cuerdas vocales perturba el aire que está a su alrededor comprimiéndolo y rarificándolo. Estas perturbaciones se propagan a través de la atmósfera que nos rodea, constituyendo una onda de sonido.

Cuando se toca algún instrumento musical lo que se está haciendo efectivamente es hacerlo vibrar. Por ejemplo, al tocar un violín se hace vibrar la cuerda con el arco; ésta a su vez hace vibrar el cuerpo de violín. Al vibrar la madera de que está hecho, el violín comprime y rarifica al aire que está junto a él. Estas perturbaciones se propagan y forman un sonido. Lo mismo ocurre con cualquier otro instrumento musical.

Cuando un objeto se rompe o choca con algún cuerpo, perturba el aire que está a su alrededor y genera una onda sonora.

Las ondas de compresión y rarefacción se propagan no solamente en el aire sino en cualquier otra sustancia. Es claro que para que esta onda se propague la sustancia debe poder comprimirse y rarificarse. Esto ocurre con cualquier sustancia, unas en mayor grado y otras en menor grado. Por tanto, una onda sonora se propaga en un medio, por ejemplo el agua, un sólido como el hierro, etcétera.

Si no hay medio entonces una onda no se propaga; así, no puede propagarse en una región en que no haya nada, en el vacío. Por ejemplo, en la Luna no hay atmósfera, es decir, no hay aire y por tanto no se propaga el sonido.

Una característica de una onda es la longitud de onda, denotada por l (Figura 17). Esta cantidad es la distancia entre dos máximos sucesivos de la onda. La longitud de onda se mide en metros, centímetros, kilómetros, etcétera.

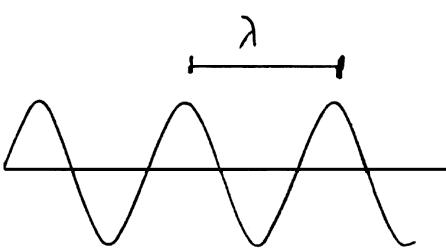
Figura 17. La longitud de onda es la distancia entre dos máximos sucesivos.

Otra característica de una onda es su frecuencia, denotada por f, que es el número de ciclos que se repite en un segundo. La unidad de la frecuencia es el ciclo/segundo que se llama hertz (abreviado Hz).

Hay una relación entre la longitud y la frecuencia de una onda; en efecto, resulta que su producto es igual a la velocidad v con que se propaga la onda.

f l=u

En vista de que en un medio dado la velocidad v es una cantidad constante, si la frecuencia f aumenta, para que el producto (fl) sea constante, necesariamente la longitud de onda l debe disminuir, e inversamente. Por lo tanto:

e inversamente:

La descripción matemática de la propagación de las ondas arriba descritas se hizo durante la segunda mitad del siglo XVIII y las dos primeras décadas del XIX. Para ello se utilizaron como punto de partida las ecuaciones de la mecánica que Isaac Newton desarrolló. Se obtuvo en cada caso la ecuación que describe la variación de la correspondiente cantidad con respecto a su valor en equilibrio. Así, por ejemplo, en el caso de la cuerda (Figura 16) se obtuvo la ecuación que debe satisfacer el desplazamiento h de la cuerda con respecto a su posición de equilibrio, en cada instante y en cada posición a lo largo de la cuerda. Se encuentra una ecuación que contiene el valor de la velocidad con la que se propaga la onda: depende de la tensión de la cuerda y la densidad de masa. De la misma manera se encontraron las ecuaciones para la propagación de las ondas en el estanque de agua y del sonido, arriba mencionadas. No escribiremos estas ecuaciones. En cada una el valor de la velocidad de propagación de la onda depende de las características mecánicas de los sistemas en cuestión. Resulta que todas las ecuaciones mencionadas tienen la misma estructura matemática. Por este motivo, a una ecuación de este tipo se le llama ecuación de onda. Por supuesto que también se estudió otro tipo de ondas, como por ejemplo las que se propagan en un tambor, etc. En cada caso se encuentra el mismo tipo de ecuación de onda. La única variante entre caso y caso es el valor de la velocidad de propagación de la onda que depende de las propiedades mecánicas particulares del sistema en cuestión. A estas ondas se les llama ondas mecánicas. A principios del siglo XIX se inició también el estudio matemático para obtener las soluciones de las ecuaciones de onda.