V. LA TURBULENCIA

Aquí vamos a considerar algunas de las ideas mencionadas con anterioridad para esbozar lo que constituye uno de los desafíos más grandes de la física, el problema de la turbulencia. El problema aparece en casi todas las ciencias experimentales y, por su formulación, en las matemáticas. La "solución" a este problema ha eludido a matemáticos, ingenieros y físicos por más años de los que el decoro permite aceptar. Los intentos de abordar el problema han generado o estimulado ramas de las matemáticas, han introducido múltiples ideas en física y han generado una gran variedad de métodos matemáticos y experimentales; todos de una utilidad notable en otras disciplinas. Muchos científicos sobresalientes estudiaron el problema y luego prefirieron cambiar de tema para lograr las contribuciones que los hicieron figurar en la historia. Por intentos no ha quedado, si bien las cosas no están como al principio.

Al iniciarse la década de los años setenta se abrieron varias perspectivas teóricas y experimentales de muy diversa índole. Cada una por separado parecía ser la adecuada para atacar en forma definitiva el problema. Cada una de ellas inició una etapa de intenso, extenso y excitante trabajo en todo el mundo. Combinando ideas y métodos recién desarrollados en las matemáticas, desde las muy abstractas como la topología diferencial, hasta las más prácticas como el análisis numérico (aunado a la construcción de computadoras cada vez más grandes y veloces), se revisaron experimentos clásicos desde una nueva perspectiva y se encontraron elementos que estaban a la vista, pero que no se habían buscado o que simplemente se ignoraban invocando diversos argumentos. También, nuevas técnicas experimentales y cuidadosas observaciones hicieron cambiar algunas ideas preconcebidas y el enfoque teórico que sistemáticamente se había estado siguiendo. Así, se revisaron las teorías y repitieron experimentos. Si bien cada una de las nuevas ideas y métodos, teóricos y experimentales, siguen en una efervescente actividad, el optimismo inicial sobre la comprensión del fenómeno de la turbulencia ha ido decayendo con el tiempo en vista de los exiguos resultados específicos. Muchas cosas han quedado más claras y los horizontes por explorar se han abierto en forma sorprendente.

Algo claro e irreversible que sucedió a lo largo de este proceso, fue el inicio de un cambio en la actitud de la mayoría de los físicos; en los que no se ha dado es porque no lo requerían o porque todavía no lo pueden aceptar.

El enfoque reduccionista de la ciencia, llevado a su culminación en la física, busca explicar todos los fenómenos con base en un conjunto reducido de leyes fundamentales. Así, la materia se redujo, pasando por las moléculas y los átomos, a las partículas elementales, los cuarks. De todas las fuerzas en la naturaleza, pasando por las eléctricas, las magnéticas, las nucleares y las gravitacionales se llegó (casi) a una sola, la gravitacional - cuántica (supersimétrica). Logrado esto, dirían (y aun dicen) pomposamente algunos, el resto es un problema de aplicaciones; esta imagen va diluyéndose poco a poco ante los hechos y la humildad regresa al lugar de donde no debió salir.

Todavía hace poco se decía que las leyes básicas habían sido encontradas en la primera mitad del siglo XX y que con esto se cerraba una etapa gloriosa del pensamiento humano (algo parecido se pensaba hace cien años con la mecánica newtoniana y el electromagnetismo de Maxwell). Aun suponiendo que conocemos estas leyes fundamentales, en forma clara y precisa, lo que sería decepcionantemente pretencioso, algo ha cambiado. Se ha puesto de manifiesto que esto no es suficiente y que para explicar el mundo se requiere mucho más.

El argumento es más o menos el siguiente. La dirección opuesta al reduccionismo, creciendo en grado de complejidad, ha traído sorpresas que muy pocos preveían. A partir de casi cualquier punto en esta dirección aparecen nuevos fenómenos, ricos y variados, con elementos ausentes en el nivel anterior, más sencillo; se generan nuevas simetrías y emergen formas nuevas de organización. Si a un nivel de descripción parece sólo haber desorden, al siguiente aparece orden en el caos, como en un acto de magia medieval donde los encantamientos son las fuerzas ocultas que nos desafían a descubrirlas. El comportamiento de grupos de átomos o moléculas parece tener poco que ver con sus elementos constituyentes, cúmulos de estos grupos tienen aún menos memoria de sus elementos básicos. Estos cúmulos se autorganizan, duplican y evolucionan solos; confabulados en grupos de cúmulos cada vez más grandes llegan a producir patrones de flujo cuya belleza adorna la superficie de algunos planetas, a ladrar en las esquinas oscuras de colonias olvidadas o se atreven a construir máquinas que empiezan a pensar sobre ellas mismas...

Comienza a verse claro que el buscar las leyes básicas de los constituyentes últimos de la materia es tan fundamental como investigar las leyes que rigen los procesos que se dan con el aumento en la complejidad de los sistemas. Casos característicos son los estudios sobre los mecanismos que dan lugar a la autorganización, a la formación de patrones, a la aparición de simetrías o a la desaparición de éstas y al orden que nace cada día en lo que sólo parece ser el caos...

Como siempre, cuando parece que se alcanza el horizonte, la naturaleza nos muestra que hay otro igualmente lejano, nuevo, más rico que el imaginado, más estimulante para ser estudiado. La investigación fundamental sigue tan abierta y hay tanto por hacer como lo había antes del descubrimiento de las leyes básicas. Los grandes pasos que se han dado en el avance del conocimiento son sobre un camino que no tiene final. En el mejor de los casos, el camino se volverá infinitamente autorreferente, como la espiral de Arquímedes o los conjuntos de Julia. Con esta frase críptica podemos ahora regresar al asunto que nos reúne.

¿Cuál es el problema y qué sabemos de él?

Todos los flujos que se observan pueden clasificarse en dos grandes grupos, los laminares y los turbulentos. Los casos más sencillos que ejemplifican a los primeros son el flujo uniforme, donde la velocidad del fluido es la misma en todos lados, y el flujo de Couette plano, ilustrado en la figura IV. 3. Los hay más complicados, como los que aparecen en las figuras II. 7, II. 8, IV. 2, IV. 4 y IV. 7. En todos estos el fluido se mueve en láminas y parece obedecer reglas más o menos claras. Estudiando los flujos laminares es como se han entendido los principios básicos que describen a los fluidos. Por otra parte, son los flujos turbulentos los que dominan el foro.

Cuando el movimiento de un fluido es irregular y complicado se dice que el flujo es turbulento. En la figura V.1 se muestra un chorro turbulento de agua; aunque muy familiar, la complicada estructura ilustra las características de la turbulencia. Esta definición, como tantas otras en nuestro negocio, no parece muy precisa: podíamos haber dejado el pudor a un lado y caracterizar simplemente a la turbulencia como el estado no- laminar. Ésta es parte de la dificultad.

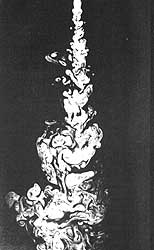
Figura V. I. Chorro turbulento de agua.

¿Cuándo es un flujo lo suficientemente complicado como para ser bautizado como turbulento? Como con el estado mental de las personas, es relativamente fácil distinguir los casos extremos. A quienes están totalmente desquiciados los confinamos a una habitación acolchonada, dejando fuera a los normales (¿?), pero siempre nos preocupa distinguir la ubicación de la línea que separa los casos marginales. A los "fluidicistas" les pasa un poco lo que a los psiquiatras (con la única ventaja de no ser sujetos de su propio estudio).

Una característica del estado turbulento es la completa irreproducibilidad de los detalles de un flujo; hay un elemento aparentemente caótico que es inherente a este estado de movimiento. Al abrir completamente la llave de un lavabo observamos un chorro de agua que cae, choca con el fondo del vertedero, se reúne con la que cayó previamente y, moviéndose de manera irregular, se va por el desagñe. Si midiéramos algún parámetro del flujo con mucha precisión, como la velocidad en el chorro encontraríamos que conforme transcurre el tiempo, tal parámetro va cambiando de valor y da lugar a un patrón como el que se muestra en la figura V.2. Si después medimos muchas veces, abriendo la llave de la misma forma, esperando el mismo tiempo y a la misma distancia de la boca de la llave, el resultado será muy parecido al anterior, pero nunca igual.

Figura V. 2. Gráfica de la velocidad (vertical) contra el tiempo (horizontal). El valor medio de la velocidad es v_o.

No sólo la velocidad cambia en esta forma irregular. Casi todas las variables hacen lo mismo. Por ejemplo, supongamos que se determina el gasto, que es la cantidad de agua que sale cada segundo, manteniendo todo fijo. El resultado sería de -digamos- un litro cada diez segundos (100 ml/s), aproximadamente; a veces unos mililitros más, a veces otros menos. Es decir, fluctúa alrededor de un valor promedio, el de 100ml/s. El asunto no tiene remedio, siempre es así cuando el valor promedio de alguna cantidad excede de cierto valor, llamado crítico. Para ciertos casos muy simples se ha logrado predecir razonablemente el valor crítico que debe alcanzar cierto parámetro (usualmente el número de Reynolds) para que el flujo pase de un movimiento laminar a uno turbulento. Es decir, que se pierda completamente la estabilidad del flujo (se vuelva un tanto loco). Por otra parte, el describir estas fluctuaciones, que podemos observar y cuantificar, es uno de los aspectos más difíciles de abordar que tiene el problema, ya que se trata de poderlos predecir, no sólo de medirlos; la medición es hoy en día un trabajo de rutina en muchos laboratorios, si bien es necesaria una tecnología relativamente complicada.

Los cientos de trabajos que se publican sobre estudios teóricos y experimentales de la turbulencia, cada año y desde hace muchas décadas, hacen que una reseña de los avances logrados se convierta en una obra de volúmenes. El uso de las más variadas técnicas experimentales y matemáticas las hace, además, de difícil lectura aun para los especialistas. Sin embargo, algunas de las ideas más viejas y más recientes, que comparten elementos, nos permiten asomarnos a este mundo agitado y convulso que llamamos turbulencia.

V.1. LA LEY DE KOLMOGOROV

Lewis Fry Richardson (1881-1953), uno de los pioneros de la meteorogía moderna y miembro representativo de la tradición científica inglesa, estudió la dinámica atmosférica y, desde luego, se enfrentó con la turbulencia, siempre presente en el monumental laboratorio de la atmósfera. En un poema sencillo, que todavía se cita en los textos, resumió lo que Da Vinci plasmó en sus lienzos al observar el fluir de las aguas y lo que los científicos creen que sucede en un fluido excitado.

Big whorls have little whorls,

which feed on their velocity;

and little whorls have lesser whorls,

and so on to viscosity

(in the molecular sense).

Vórtices grandes tienen vórtices más chicos,

nutridos por su velocidad.

Vórtices chicos tienen vórtices más chicos,

así hasta la viscosidad

(en el sentido molecular).

Dejando a un lado el adagio latino de "traductor, ñtraidor!", el contenido del verso expresa el proceso que parece sufrir la energía que se le comunica a un fluido para mantenerlo en estado turbulento, el llamado modelo de la cascada de energía.

Imaginemos un tanque con agua, a la que agitamos con una paleta de cierto tamaño (escala). Al mover la paleta se producen vórtices de la misma escala. Observamos que estos vórtices migran y se desintegran, generándose en el proceso otros vórtices de una escala menor. Este mecanismo se continúa de una escala a otra, hasta que la escala es lo suficientemente pequeña como para que el movimiento de los vorticillos resultantes sea dominado por los efectos de la fricción interna del fluido, la viscosidad. Ahí, los pequeños remolinos comienzan una etapa de decaimiento, disipándose hasta desaparecer; la longitud típica de esta última escala es de fracciones de milímetro.

De acuerdo con estas ideas, la energía pasa de una escala a otra, como en una cascada en la que el agua cae de un nivel a otro, perdiendo altura (energía potencial) pero ganando movimiento (energía cinética). En el fondo de las escalas el movimiento se convierte en calor, disipándose la energía, y queda el fluido en reposo. En la medida en que se siga agitando la paleta (inyectando energía al fluido) se podrán apreciar las estructuras en las distintas escalas, siendo la más pequeña la más difícil de ver.

Por consiguiente el estudio de la dinámica de vórtices es uno de los más importantes en los trabajos de turbulencia. El objetivo es entonces entender cómo se generan, cómo interaccionan entre sí, cómo se rompen y, finalmente, cómo decaen. Algunas de las teorías más comunes abordan estos problemas desde diversos puntos de vista, tratando de encontrar cantidades que se conserven en este proceso y estudiando la forma en que van cambiando otras, al pasar a través de las distintas escalas.

Uno de los resultados más célebres en la teoría de la turbulencia se debe a Andrei Nikolayevich Kolmogorov (1903-) y a A. M. Obukhov, quienes obtuvieron el mismo resultado, en forma independiente, en 1941. La importancia de la expresión se debe a que es uno de los pocos resultados generales y cuantitativos y a que es válida para todo flujo turbulento isotrópico y homogéneo. Que la turbulencia sea homogénea significa que se ve igual si nos trasladamos a distintos puntos del fluido; que sea isotrópica quiere decir que parece igual si vemos en cualquier dirección. Para que lo anterior sea (aproximadamente) cierto se requiere que la región en estudio se encuentre lejos de objetos o de las paredes que contienen al fluido; se dice entonces que la turbulencia es localmente isotrópica. Esta simplificación fue introducida por Geoffrey Ingram Taylor (1886-1975) en 1936. Muchas ideas fundamentales en la dinámica de fluidos moderna fueron propuestas por Taylor en los profundos trabajos que hizo a lo largo de su prolífica carrera científica.

Kolmogorov, quien era un distinguido matemático soviético, fundador de la teoría moderna de la probabilidad, logró atraer la atención de numerosos colegas hacia la teoría de la turbulencia. Al ver la naturaleza física, más que matemática, de la contribución de Kolmogorov, la mayoría optó por volver a sus intereses originales.

Curiosamente, el mismo resultado fue obtenido en 1948 por tres físicos del más alto nivel, en forma independiente y por caminos diferentes. Werner Karl Heisenberg (1901-1976) y Karl Friedrich von Weizsacker (1912), durante su detención en Inglaterra con otros científicos alemanes, y Lars Onsager (1903-1976), en los EUA. Como ha sucedido en otros casos, la ley descubierta por estos investigadores debía llevar como nombre un anagrama con sus iniciales, algo como wookh; afortunadamente no fue así.

La famosa expresión establece en forma cuantitativa varios aspectos relacionados con la cascada de energía propuesta por Richardson. Para percibir la esencia del resultado seguiremos a Kolmogorov en su razonamiento. Empezaremos por formular el resultado, que parece más un criptograma de la Guerra Fría que una descripción de lo que puede pasarle a un fluido. Después, intentaremos descifrarlo.

La ley de los dos tercios de Kolmogorov, como se le conoce, afirma lo siguiente. En un flujo turbulento, la autocorrelación de velocidades entre dos puntos separados por una distancia l, dentro del subintervalo inercial, es igual a C(l) ^2/3; C es una constante numérica universal y es el flujo promedio de la energía (por unidad de masa). Todo indica que para entender el enunciado harían falta estudios serios de paleología. Realmente no es así, es suficiente con algo de física y de matemáticas; para apreciar el sabor basta un poco de paciencia.

La cascada de energía "a la Richardson", sugiere la existencia de una serie de escalas a través de las cuales la energía transita, hasta disiparse en calor. En la escala más grande, las estructuras (vórtices) llevan "impresa" la forma en que fueron generadas. Chorros y estelas ejemplifican este hecho; cada uno parece estar estructurado de manera muy distinta. A este nivel, son aspectos como la geometría del sistema los que definen el tamaño y la forma de los vórtices portadores de la mayor parte de la energía. En el otro extremo, los vorticillos más pequeños consumen toda la energía al disiparse por efecto directo de la viscosidad. En este proceso de cascada, en el que las estructuras se van descomponiendo en otras más pequeñas, el flujo va perdiendo la memoria del mecanismo generador de la turbulencia.

Con estas ideas en mente, Kolmogorov introduce su primera hipótesis. Propone la existencia de un intervalo de escalas en el que el comportamiento turbulento es universal (olvidó sus orígenes...). Es decir, el flujo turbulento es homogéneo, isotrópico y estacionario. Este último atributo indica que, en promedio, el estado no cambia con el tiempo; la amnesia es permanente, digamos. Además, nos asegura el abstracto pensador, en este intervalo las cosas no pueden depender más que de dos parámetros: el flujo de energía () que se le inyecta al flujo para mantenerlo agitado (algo así como el sufrimiento que experimenta el que mueve la paleta o sopla el chorro) y la viscosidad (v), que caracteriza la disipación de la energía (el calentamiento del fluido).

Hecha esta suposición, recurre a algo muy ingenioso. Estima el tamaño de la escala máxima para la cual los efectos de la fricción todavía desempeñan un papel. Al efecto demuestra que sólo hay una manera de combinar los parámetros y v para que formen una longitud, ñasí de simple! (sólo con propósitos morbosos cito el resultado: ()-^1/4 v^3/4). La escala así determinada, que con suma originalidad fue bautizada de Kolmogorov, se denota por h.

Entonces - se atreve a postular de nuevo- a escalas mayores que h no hay disipación, por lo que la viscosidad debe ser una cantidad irrelevante. De esta manera, hay una zona de escalas (subintervalo) en la que v debe desaparecer, quedando como el único parámetro importante. La energía inyectada para mantener la turbulencia se va transfiriendo a escalas cada vez más chicas, hasta aparecer una envidiable amnesia. Sigue pasando a escalas todavía más pequeñas, hasta que la viscosidad aparece en la escena, iniciando su destructivo papel, y luego el final fatal, que a todo le llega. Como la energía sólo transita por estas escalas intermedias, al subintervalo se le llama inercial, ñcomo de paso!

Así, en la traducción de la ley de los dos tercios se aclara un poco lo de subintervalo inercial y el significado de . Sigamos adelante con la interpretación.

En un flujo turbulento la velocidad cambia (fluctúa) en el tiempo y en el espacio. Es decir, al medir la velocidad en un punto fijo del espacio, conforme transcurre el tiempo, se obtienen datos como los que se muestran en la figura V.2. Un patrón semejante se obtiene si se mide la velocidad, simultáneamente, en varios puntos. Desde luego, el promedio de la fluctuación es cero; igual aumenta que disminuye, o se mueve a uno u otro lado.

¿Qué tan independiente es el valor que tiene la velocidad en un punto del que tiene en otro punto o del valor que tomó tiempo antes? La respuesta a esta pregunta se encuentra en la autocorrelación de las velocidades, espacial o temporal, respectivamente. Nos dice cómo están (cor)relacionados los valores de la velocidad (el prefijo auto indica que es la correlación de una cantidad dada consigo misma). Si los puntos están muy cercanos, es de esperarse que exista alguna conexión entre los valores de la velocidad, mientras que si están muy separados probablemente no tendrán relación alguna. En lenguaje técnico se dice que la autocorrelación de las velocidades decae con la distancia. Por ejemplo, mi autocorrelación temporal de memoria es de corto alcance; hay quienes aseguran que no pasa mucho tiempo para que mis recuerdos sean cada vez más vagos...

Regresando a la ley de los dos tercios, podemos resumirla de la siguiente manera. Primero, existe una escala a partir de la cual el movimiento turbulento es independiente de la forma en que se generó. Segundo, para dos puntos en el fluido separados por una distancia l, las velocidades están relacionadas. Tercero, si la escala de l es suficientemente grande, los efectos disipativos (la viscosidad) no desempeñan un papel determinante. Cuarto, la relación entre las velocidades (su producto) depende, a lo más, de y de la distancia l. Al recapitular hemos introducido dos puntos adicionales. Uno, que la autocorrelación está definida como el promedio del producto; aunque es importante este punto, no es necesario entrar en más detalles. El otro consiste en proponer la dependencia exclusiva en y l. Si l está en el subintervalo inercial, cualquier cantidad dependerá sólo de , como parámetro característico del flujo.

El último ingrediente para obtener el resultado de Kolmogorov es el argumento dimensional. Nuevarnente, la única forma de combinar y l para que formen el producto de dos velocidades (una autocorrelación) es... ñla escala de Kolmogorov! El factor restante sólo puede ser un número (sin dimensiones, igual para los que miden en pies, que para los civilizados que miden en metros) y, no sabiendo cuánto valía, le llamó C. Los experimentos indican que su valor es cercano a 0.5.

Los intentos por extender las ideas de Kolmogorov, Obukhov, Heisenberg, Von Weizsñcker y Onsager han sido hasta ahora infructuosos. Las extensiones han requerido de aparatos matemáticos formidables y en ellas el esfuerzo realizado contrasta con los escasos resultados o lo poco significativo que son. Una de ellas fue desarrollada por Robert H. Kraichnan, durante los años cincuenta y sesenta, con técnicas importadas de la teoría cuántica del campo, desarrolladas para el tratamiento de fenómenos relacionados con las partículas elementales.

En un contexto distinto aparecieron los enfoques de la siguiente década, la de los setenta. Las ideas de estructuras coherentes, de atractores extraños y de fractales generaron un frenesí que todavía no acaba, aunque el optimismo inicial ha disminuido. Aún es prematuro hacer una evaluación justa de la repercusión de las ideas actuales sobre el problema de la turbulencia; todavía hay muchas esperanzas y es posible que alguien sepa combinarlas en las proporciones adecuadas para dar el siguiente gran paso. Con la sobriedad y la madurez que sólo vienen con el tiempo se podrá apreciar la perspectiva con más objetividad. Veamos en qué consisten algunas de estas ideas.

V.2. ESTRUCTURAS COHERENTES

La tecnología usada en la investigación experimental se ha mantenido en constante desarrollo a través del tiempo. Una parte considerable de la llamada tecnología de punta ha sido el fruto de las necesidades específicas de la investigación en diversos campos de la física; tristemente, han sido las aplicaciones a la industria de la violencia las que han sido argumentadas para justificarla y el motor para su desarrollo.

El uso de computadoras cada vez más grandes y veloces, de electrónica cada vez más rápida y versátil, de sondas mecánicas, ópticas y acústicas más complejas y delicadas han dado lugar a una revolución en la forma de hacer experimentos en las ciencias naturales. Los laboratorios dedicados al estudio de la turbulencia no son la excepción, es más, son un excelente ejemplo. No sería exagerado afirmar que, por ejemplo, el desarrollo de computadoras cada vez más grandes ha tenido como principal promotora a la dinámica de fluidos. Sin embargo, aún no existe un problema de turbulencia que se pueda solucionar con la computadora más grande disponible, aunque ya se empiezan a acercar...

Al iniciarse la era de la electrónica moderna, acoplada a sistemas de adquisición de datos y técnicas de medición y visualización, basadas en la óptica de láseres, se llevaron a cabo algunas observaciones que influyeron decisivamente en la investigación de la turbulencia. Curiosamente, éstas se realizaron con métodos ópticos sencillos que se venían usando por décadas. El descubrimiento central fue que la mayoría de los flujos turbulentos no son tan irregulares como se creía; dentro del evidente caos hay cierto orden en el movimiento del fluido. Al azar, aparecen estructuras con características bien definidas estadísticamente: la distribución de sus escalas, sus tiempos de vida (periodos), etcétera.

Estos sorprendentes resultados dieron lugar a una reconsideración profunda de los experimentos que se venían realizando. Una calificación más cuidadosa de la estructura espacial de cada flujo turbulento se hizo necesaria para llegar a entender las observaciones (Figura V. 1).

Nuevamente se repitieron experimentos y se formularon otros para delinear las propiedades de estas formas semiordenadas que parecían pulular entre el caos. La explosión en la capacidad de cómputo, que todavía no acaba, vino a dar mayores posibilidades a este nuevo giro experimental. Las medidas más extensas que se hacían con anterioridad eran autocorrelaciones de la velocidad, lo que daba lugar a que, al observar en dos puntos distintos y promediar el resultado, se borraran estas estructuras; las medidas tendían a registrar estados distintos de estas estructuras que poco tenían de relación unas con otras. Al promediar entre pulpos y niños se obtienen seres que en promedio tienen seis apéndices; este dato promedio no parecería ser muy útil a un observador externo. Así, la forma de medir y sobre todo, de analizar los datos, sufrió un cambio de fondo.

Un huracán que se mueve en el Océano Atlántico, visto desde un satélite orbital a 300 km de distancia, parece una estructura (vórtice) perfectamente organizada, regular, que se mueve lentamente. Para el capitán de una nave camaronera y para sus asustados tripulantes, que lo ven en una escala de metros, o decenas de éstos, parece un infierno húmedo e irregular que varía violentamente de un lugar a otro y de un instante al siguiente. Ni lo ven muy organizado (excepto para ahogarlos) ni lo ven variar lentamente. Esta estructura coherente, vista por el astronauta, está conformada por miles de vórtices más pequeños en plena algarabía, que sufre el argonauta.

En la figura V.3 se ilustra una de las primeras fotografías que exhibían estas estructuras coherentes. En ésta se pone de manifiesto una estructura bidimensional de vórtices sobre la que hay superpuesta una complicada trama de vorticillos (la turbulencia). El flujo corresponde a lo que se llama la capa de mezclado. Dos fluidos, uno arriba y otro abajo, se mueven de derecha a izquierda con velocidades distintas. En este caso se trata de nitrógeno (arriba) y de una mezcla de helio y argón (abajo). Las velocidades son de 1 000 cm/s y de 380 cm/s, respectivamente, y la presión es de 8 atmósferas. La fotografía fue tomada por el grupo de Anatol Roshko, en la década de los setenta, usando un método que podríamos llamar sombragrafía.

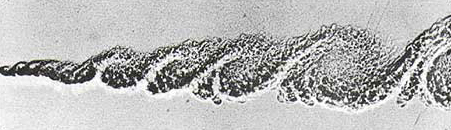
Figura V. 3. Estructuras coherentes en un flujo turbulento; capa de mezclado.

El procedimiento para obtener estas fotografías es relativamente sencillo y el fenómeno que lo genera es muy común. Quien ha visto una fogata o un montón de brasas encendidas, recordará que las imágenes que se ven del otro lado parecen bailar; sobre un fondo claro y uniforme pueden verse ciertas sombras irregulares, como ondas de calor. El efecto es producido por las variaciones que sufre la dirección de la luz al pasar por regiones con temperaturas distintas. Al aumentar la temperatura del aire, éste se expande, cambia su densidad y tiende a moverse hacia arriba. La luz que va pasando, tan rápido que ni se entera que se mueve el aire, modifica su dirección al pasar de un medio más denso a otro menos denso; decimos que cambia el índice de refracción. Las zonas de diferente densidad, irregulares en forma, generan un patrón tembloroso de imágenes. En el flujo en cuestión, cada uno de los fluidos tiene un índice de refracción distinto y deja pasar a la luz de diferente manera. Así, en la región de mezclado turbulento hay una complicada combinación de ambos índices de refracción y la luz sigue estas variaciones. Al poner una pantalla del otro lado del flujo se pueden ver los patrones resultantes (una criatura con una cámara fotográfica de plástico puede hacer el resto).

Es interesante notar que destacados investigadores habían estudiado este flujo y habían determinado todo lo que entonces se consideraba necesario para caracterizar sus propiedades estadísticas. Descubrir la existencia, persistencia y evolución de estas estructuras, en lo que parecía un flujo sin orden alguno, fue una verdadera revelación.

La caracterización de estructuras coherentes sigue siendo el gran tema de actualidad en la investigación experimental. La parte teórica se encuentra todavía en sus inicios, cosa no del todo rara en este churrigueresco problema. Los intentos por elaborar una explicación cuantitativa de estos fenómenos siguen desafiando a la imaginación y al colmillo de la comunidad científica que se interesa en el problema. Las dificultades se inician desde la forma de definir matemáticamente a estas criaturas que viven en el caos. Si recordamos que la definición de un vórtice sencillo nos elude todavía, no es de sorprender que este asunto le quite el sueño a más de uno.

Hay la sospecha fuerte de que una de las mejores formas de acorralar a las elusivas estructuras coherentes es estudiar el problema en términos de la vorticidad, y los enfoques teóricos se mueven en esta dirección. De esta manera, los experimentales tratan de medir la vorticidad y los teóricos de ver cómo se distribuye en el espacio y el tiempo. Aquí, de nuevo, los investigadores depositan sus esperanzas en las computadoras. Los experimentales, para la adquisición, manejo y análisis de grandes cantidades de datos; sin ellas, este trabajo tomaría cientos de miles de años, de todos aquellos que trabajan en el tema, ñpara un solo caso! A los teóricos les pasa algo semejante. Para todos se ha convertido en la herramienta indispensable y la fuente de inspiración para muchos estudios, desde las simulaciones directas de flujos sobresimplificados hasta el terreno de juego para los experimentos pensados.

El estado actual de esta situación es todavía nebuloso (ñturbulento!), si bien hay múltiples ideas cualitativas sobre el papel que desempeñan las estructuras coherentes. Estas ideas platicadas son el motor del trabajo experimental y teórico que se puede consultar en la bibliografía especializada. La forma de plantear matemáticamente lo que sugiere la intuición y la información acumulada es parte de la tarea para llevar a casa.

El problema continúa abierto y ofrece la posibilidad de ganarse el pan cotidiano a muchos curiosos y necesitados de la ciencia y el conocimiento, ya sea motivados por razones prácticas o estéticas.

V.3. ATRACTORES EXTRAñOS Y CAOS

Una serie de revolucionarias ideas y de descubrimientos paralelos a los anteriormente descritos, independientes, diferentes y aparentemente desconectados, pero sobre el mismo problema general de la turbulencia, ocurrieron en la misma prolífica década en que se descubrieron las estructuras coherentes. Describiremos sólo una parte, pero no tocaremos las sugerentes ideas e importantes teorías como las de Mitchel Feigenbaum, Benoit Mandelbrot, Pierre Manneville e Yves Pomeau.

Uno de los antecedentes fue el descubrimiento hecho por otro meteorólogo, Edward N. Lorenz, en 1963. Estaba interesado en comprender ciertos aspectos de la atmósfera terrestre con el propósito de avanzar en los métodos para la predicción del tiempo. Con esto en mente elaboró un modelo muy sencillo para estudiar lo que le pasa a un fluido sometido a una diferencia de temperaturas en presencia del campo gravitacional, conocido como el problema de Rayleigh- Bénard. A partir de las ecuaciones básicas de la mecánica de fluidos, las de Navier- Stokes, introdujo varias hipótesis para reducir las ecuaciones a lo que en su opinión aún tenía elementos suficientes para generar una dinámica interesante. Luego, procedió a resolverlo en forma numérica. Cuál no sería su sorpresa al encontrar que, para ciertos valores de los parámetros que caracterizaban al problema, la solución mostraba un comportamiento errático. Curiosamente, no tiró a la basura los resultados.

¿Cómo era posible que el resultado de una ecuación, compuesta por términos bien definidos y perfectamente regulares, diera lugar a un comportamiento no determinista? Otros, seguramente, hubieran descartado los resultados y pensado que había algo equivocado con el método de solución o con la computadora misma. Para Lorenz había algo nuevo y profundo en lo que acababa de encontrar; había descubierto a los atractores extraños. Pasaron varios años para que la comunidad cientifica se percatara de la enorme importancia de su hallazgo. Baste decir que gracias a su trabajo, ahora sabemos que nunca podremos predecir el tiempo más allá de siete días. Si oímos que se espera buen clima para la semana próxima, podemos asegurar que es precisamente eso, una esperanza.

A la impredictibilidad del clima a largo plazo se le ha dado por llamar el efecto mariposa. La razón para este nombre proviene del hecho de que una pequeña diferencia en las condiciones iniciales digamos, hoy dará lugar a una profunda diferencia a lo que puede estar ocurriendo tiempo después. El efecto de la imperceptible variación irá creciendo con el tiempo, acumulándose poco a poco, como una avalancha; para exagerar el punto, se dice que el aleteo de una mariposa modificará el clima en unos meses. Desde luego, aquí nos referimos a la predicción detallada de las condiciones meteorológicas después de unos días. Características burdas o promediadas sobre muchos eventos y muchos años no se verán modificadas en forma sustancial por estos pequeños mariposeos; la erupción de un volcán o la desmesurada producción de contaminantes en alguna región hipotética del planeta, no estarían incluidos entre estos últimos. La temporada de lluvias será igual, si por ello entendemos que es parecida a la temporada del béisbol; no tienen fechas fijas y los caprichos de los protagonistas respectivos siempre están presentes.

¿Qué es un atractor extraño? Veamos primero qué son los no extraños, por extraños (o triviales) que parezcan.

Si estiramos un resorte con una canica de cada lado y lo soltamos dentro del agua, observaremos que empieza a oscilar y que poco a poco se va parando. Si hacemos la misma prueba fuera del agua, en el aire sucio que algunos respiran, sucede lo mismo, aunque el amortiguamiento será mucho menor y se tardará más en detenerse. Decimos que la disipación es menor en este caso. Si lo pudiéramos hacer en el vacío, tardaría más en detenerse; habríamos reducido aún más la fricción. Al cambiar el material del que está hecho el resorte por uno más elástico (más caro), la disipación podría reducirse aún más. A pesar de que nunca podríamos quitar la fricción (disipación) por completo, podríamos ver que cada vez tarda más en detenerse. En condiciones ideales se quedaría oscilando ad infinitum. Estas observaciones ilustran el punto siguiente.

El estado final de un resorte (oscilador) es el reposo total o la oscilación perenne. ñPues que trivialidad!, decimos todos. La ventaja del ejemplo, que no es el único, es que todo puede hacerse con un lenguaje matemático preciso y entonces puede demostrarse que los movimientos posibles tienden (son atraídos) a un punto, el del reposo. Este estado final es un atractor y su dimensión es cero.

En el espacio en el que viven estos movimientos, que llamamos variedades, hay diferentes tipos de atractores: puntos (como en el caso de osciladores con fricción), curvas (como en el caso de los osciladores no amortiguados, de dimensión uno), superficies (de dimensión dos), etc.; objetos más o menos simples. Antes de Lorenz se creía que todos eran de este tipo y fue entonces que aparecieron los extraños, que resultaron ser cosas (variedades) conocidas, aunque eran consideradas como curiosidades matemáticas sin conexión alguna con el mundo real. Baste decir que su dimensión no es ningun número entero (si no serán raros).

Para poder imaginar a los atractores extraños es conveniente mencionar una de sus principales características, la de ser autosemejantes, lo cual en este caso significa que mientras más le vemos menos enseña, o que enseña lo mismo (por algo son extraños). Un objeto autosemejante que puede ilustrar (¿confundir?) la autosemejanza y que tiene una dimensión fraccionaria (fractal), es lo que se conoce como el conjunto de Cantor y se construye de la siguiente manera.

Consideremos el segmento de recta del cero al uno (Figura V.4). Lo dividimos en tres partes iguales y quitamos la del centro (segundo renglón de la Figura V.4). Ahora, a cada segmento restante lo dividimos en tres y volvemos a quitar los tramos centrales (tercer renglón). Luego repetimos este proceso hasta el cansancio y... le seguimos ad nauseam. El resultado es algo que tiene la propiedad de que si lo vemos parece una serie de puntitos con cierta distribución espacial que no alcanzamos a distinguir claramente. Si tomamos una parte y la amplificamos cien veces —digamos— se ve una serie de puntitos con cierta distancia... ñexactamente igual! No importa cuánto o cuantas veces amplifiquemos, ñsiempre se verá igual!

Figura V. 4. Conjunto de Cantor.

Un atractor extraño, llamado de Henón-Heiles en honor a sus descubridores en un modelo astrofísico, se muestra en la figura V.5. Se han hecho varias amplificaciones que exhiben parte de su estructura. En el problema correspondiente, todos los movimientos son atraídos por el atractor.

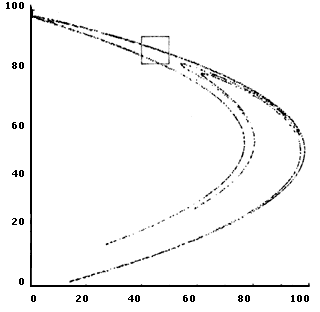
Figura V. 5. (a) Atractor de Henón-Heiles. Forma general.

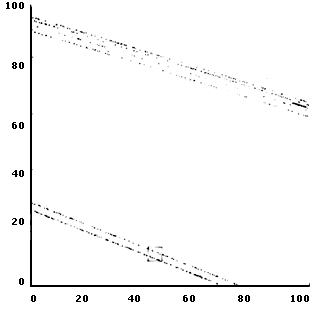
Figura V. 5. (b) Atractor de Henón-Heiles. Amplificación del recuadro de la parte (a).

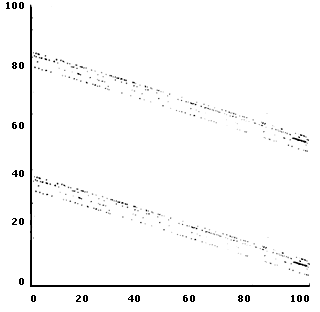
Figura V. 5. (c) Atractor de Henón-Heiles. Amplificación del recuadro de la parte (b).

En 1971, David Rouelle y Floris Takens propusieron una nueva teoría de la turbulencia basados en el descubrimiento de Lorenz. En 1978 Rouelle y Takens, en colaboración con Steven Newhouse, publicaron una importante extensión a la teoría y es la versión que ahora se maneja. La propuesta ha permitido cambiar el marco conceptual desde el que contemplamos el problema de la turbulencia, aunque su utilidad práctica para describir la turbulencia totalmente desarrollada se ve tan cercana como la colonización de la galaxia más cercana; es cosa de tiempo, un tanto largo, desde luego. El resultado fue una verdadera explosión de trabajos teóricos y experimentales sobre el tema, abriéndose por completo un área de investigación que se había circunscrito a los iniciados en matemáticas relativamente complejas.

¿Cuál era el dogma aceptado?

Lev Davidov Landau (1908-1968), tal vez el más brillante físico soviético, famoso por sus profundos trabajos en la más variada gama de temas de la física, publicó en 1944 un célebre artículo. En éste propuso un modelo sobre la forma en que se genera la turbulencia en todos los flujos. En forma esquemática, la idea era que si en cierto flujo se iba aumentando el parámetro básico, como el número de Reynolds, el estado de movimiento cambiaría con el tiempo a otro de naturaleza un poco mas complicada. Al seguir aumentando el parámetro de nuevo ocurriría un cambio en la estructura del flujo, y así sucesivamente. A la larga decía, el flujo es lo suficientemente complicado como para que se vea turbulento.

Por ejemplo, en el flujo alrededor de un cilindro, inicialmente laminar (Figura II. 7 y II. 8), se observa que al aumentar la velocidad con la que llega el fluido se transforma en otro flujo, también laminar, con más estructura. A mayor velocidad los vórtices posteriores se desprenden y aparece una estela hermosa y compleja, difícil de describir matemáticamente (Figura V.6). Al continuar el proceso la estela se va complicando hasta verse completamente turbulenta.

Figura V. 6. Estela detrás de un cilindro circular en flujo uniforme. La velocidad del flujo es mayor que en los casos de las figuras II. 7. Y II. 8.

La teoría de Landau, de carácter esencialmente cualitativo, prevaleció hasta la década de los setenta. Hoy en día tiene sólo valor histórico; sin embargo, motivó numerosos trabajos para estudiar estas transiciones y sirvió para desarrollar diversos métodos matemáticos para atacar el problema. Lo anterior, que parecía perfectamente plausible, fue modificado por Rouelle y Takens; su teoría, construida sobre bases conceptuales y matemáticas más sólidas también es, por lo pronto, de carácter cualitativo. Vencer las dificultades para utilizarla en forma explícita para hacer predicciones concretas es un proyecto a futuro. Si bien la teoría parece sumamente abstracta (matemática), las ideas físicas pueden verse con relativa sencillez. Estas pueden resumirse en dos principales.

El primer resultado sobre el que está construida la teoría es la demostración de que las ecuaciones de Navier-Stokes tienen dependencia sensible en las condiciones iniciales. Esto quiere decir, en términos normales, que todo lo que le pasa a un fluido depende de los detalles de su estado inicial. Más directo, que los fluidos tienen muy buena memoria cuando se les excita demasiado. Lo que hacen depende de cómo empezaron.

Esto explica por qué cada vez que se empieza un flujo dentro de un túnel de viento, por ejemplo, se observan patrones muy diferentes. Sucede que nunca podemos repetir un experimento exactamente en la misma forma; siempre partimos de un estado muy parecido, pero no del mismo. Todo tiene que ver con la forma en que un movimiento va a evolucionar; la contaminación del aire en el túnel, la deformación nocturna del dispositivo mecánico y, podría argumentarse, el humor del investigador. Ernst Mach (1838-1916), uno de los profundos pensadores sobre el quehacer científico, hubiera estado fascinado por tal resultado; el llamado principio de Mach, en pocas palabras, postula la influencia de cada parte del Universo sobre el resto. Esto, "aunque usted no lo crea", le ocurre a los queridos fluidos; algo así tenía que andar pasando.

De hecho, desde el siglo XIX, James Clerk Maxwell fue explícito al respecto cuando decía: "Es una doctrina metafísica que de las mismas causas se siguen los mismos efectos... Pero es poco útil en un mundo como éste, en el que las mismas causas nunca se repiten y nada ocurre dos veces..." Luego agregaba: "[....] el axioma físico análogo es que de causas semejantes se siguen efectos semejantes. Ahora hemos pasado de la igualdad a la semejanza, de la certeza absoluta a la burda aproximación [...]; cuando sucede, el curso de los acontecimientos es estable. Hay fenómenos más complicados en los que ocurren inestabilidades [...] que aumentan rápidamente con el número de variables relacionadas". Con la intuición que lo llevó al Olimpo de la ciencia, concluía: "[...] el estudio de las singularidades y las inestabilidades, más que el de las cosas continuas y estables, tal vez elimine el prejuicio en favor del determinismo [...]."

La segunda parte de la receta para cocinar la teoría de Rouell-Takens-Newhouse está ligada muy de cerca con el punto anterior. El meollo del asunto radica en que las ecuaciones de Navier-Stokes tienen atractores, como casi todas las ecuaciones, pero que resultan ser de los extraños; esto sucede en el espacio (variedad) en el que se encuentran sus posibles soluciones. Así, el movimiento de un fluido se va transformando en otros al ir cambiando el número de Reynolds, a la Landau. Pero, y aquí es donde cambian las cosas, al ocurrir el tercer cambio es muy probable que el flujo sea turbulento. Matemáticamente se dice que la solución que describe el tercer estado de movimiento está cerca de un atractor extraño. En estas condiciones las cosas se van a ver por demás extrañas (o sea turbulentas). Veamos un poco más de cerca la razón.

Digamos que la forma del atractor es la que se ilustra en la figura V.5. El estado inicial del fluido corresponde a un punto cualquiera en el papel de la gráfica; el punto escogido podría describir un movimiento regular y sencillo que no cambia en el tiempo.

Ahora cambiamos el número de Reynolds (abrimos más la llave, digamos) lo suficiente como para que el estado de movimiento cambie a otro estado (cambiamos de punto en la gráfica). Si está lejos del atractor, desde luego que será atraído a él. Repetimos el proceso y... se acerca al atractor (como en las novelas de terror). La siguiente ocasión en que repetimos la operación el movimiento cambia, muy probablemente, a uno turbulento. Visto en la gráfica, el punto se acercó tanto que empieza a moverse sobre la curva ilustrada; va cambiando en el tiempo. Como sólo lo podemos ver cada cierto tiempo (con la vista, menos de treinta veces cada segundo), parecerá brincar de un lugar a otro, sin ton ni son, siendo que en realidad se mueve sobre el atractor que se muestra.

Cuando parece que el estado es uno que se registró anteriormente, en realidad es uno parecido que se encuentra en otra parte de la curva; en una amplificación parecería estar en una de las líneas adyacentes. En realidad no es ni curva ni superficie..., es un atractor extraño.

Al publicarse la teoría, los investigadores pensaron que las cosas eran demasiado abstractas como para tener conexión alguna con los experimentos. Después de todo, a pesar de que los autores tenían un reconocido prestigio, se trataba de matemáticas muy complicadas. Al irse traduciendo la teoría al lenguaje de los interesados en el tema, se vio que había formas de poner a prueba algunas de las afirmaciones de la teoría.

Varios investigadores se dieron a la tarea de reexaminar, con las nuevas ideas, algunos flujos conocidos; unos años después, Jerry Golub y Harry Swinney, experimentales reconocidos en el campo de los superfluidos, habían logrado demostrar que había un flujo que seguía el camino que insinuaba la teoría. Reinterpretando observaciones anteriores, encontraron que tras de un par de cambios, el flujo perdía la brújula y su estabilidad; en su locura exhibía la turbulencia en forma descarada y de la manera esperada.

Los experimentos consistieron en estudiar los patrones de flujo que ocurren cuando se pone agua entre dos cilindros concéntricos y uno de éstos se pone a girar (Figura V.7(a)). Este arreglo se conoce como el flujo de Couette-Taylor, recordando a quien lo estudió por primera vez y a quien mejor lo hizo, respectivamente. Lo que ocurre en este sencillo arreglo es sorprendente.

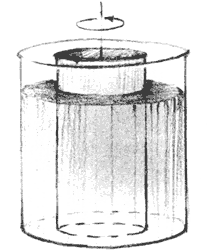
Figura V. 7. (a) Flujo de Couette-Taylor. Diagrama del arreglo experimental.

Al ir aumentando la velocidad con la que gira el cilindro interior, con el cilindro exterior fijo, se llega a un valor para el cual el fluido deja de dar vueltas en órbitas circulares alrededor del cilindro. Ahora se mueve siguiendo una trayectoria que -puede decirse- está enrollada en la superficie de una dona contenida entre los cilindros. Observando el sistema se aprecian estas donas, bautizadas celdas de Taylor, a todo lo largo del cilindro exterior (Figura V.7(b)); ésta es la primera transición. El patrón se hace visible cuando se agregan al agua partículas pequeñas.

Figura V. 7. (b) Flujo de Couette-Taylor. Celdas de Taylor.

Al seguir aumentando la velocidad de giro aparece un patrón de celdas de Taylor moduladas. Como si distintas partes de las donas quisieran ir hacia arriba y parte hacia abajo; una especie de onda congelada se superpone a las celdas de Taylor. Esta segunda transición se puede apreciar en la figura V.7(c). Luego, se viene abajo el espectáculo y hace su aparición la turbulencia.

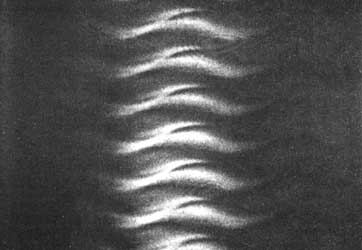
Figura V. 7. (c) Flujo de Couette-Taylor. Celdas de Taylor moduladas.

Un movimiento caótico alrededor del cilindro es lo único que sobrevive del flujo (Figura V.7(d)).

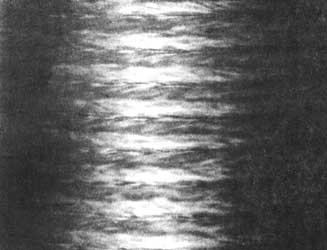
Figura V. 7. (d) Flujo de Couette-Taylor. Régimen turbulento.

Como lo indica la nueva teoría, después de un par de transiciones aparece la turbulencia. Desechada la teoría de Landau, heredó el foro la nueva prima donna (excepto que ahora no está sola...); pero al igual que con los aplaudidos artistas, deportistas, etc., su tiempo dura en tanto llegan los nuevos.

Como dijera hace unos años Uriel Frisch, destacado físico contemporáneo: "Yo creo que tenemos un conocimiento peor sobre lo que sucede en un milímetro cúbico de agua, que sobre lo que ocurre en el interior del núcleo atómico." Sabiendo que se refería al problema de la turbulencia, como prototipo de esta ignorancia crasa que cargamos sobre los hombros, no puede uno menos que compartir su visión.

Una anécdota sobre este punto la debemos a Sir Horace Lamb (1849-1934), destacado investigador inglés en el campo de la mecánica de fluidos. En un homenaje internacional que se le brindó al cumplir los ochenta años, en 1929, declaró lo siguiente: "Cuando muera, espero ir al cielo. Ahí, espero ser iluminado sobre la solución de dos problemas, la electrodinámica cuántica y la turbulencia. Sobre el primero, soy muy optimista..." En cuanto al segundo esperamos que Lamb haya ido al cielo. Seguramente así sabrá la respuesta del primero. Cabe agregar que el primero fue resuelto por uno de los grandes físicos de este siglo, Richard P. Feynman (1918-1988), por lo que le fue otorgado el premio Nobel en 1965. En palabras de Feynman: "la turbulencia es el último problema importante por resolver de la física clásica."