V. EN DONDE SE COMPARAN BORLAS ANTIGUAS Y QUIETAS CUANDO SE ASISTE A UNA CONFERENCIA Y SE TOMA EL TÉ CON UN SOLTERO ELEGIBLE. EN DONDE EL DÍA ÚLTIMO DEL AñO SE COMPARAN VOLÚMENES Y SE DISCREPA, PERO UN ERUDITO RESUELVE LA DISCREPANCIA.
DESPUÉS de haber invertido un buen rato en su arreglo personal, nerviosa, la señorita Clara tomó su paraguas, le dio un último toque a su peinado ante el espejo de la entrada y advirtió a su madre:
—Tardaremos dos horas, una de la conferencia y la otra es posible que se pase en atender a las preguntas de los asistentes, además regresaremos por la orilla del río y como te lo imaginarás caminaremos despacio. Ya dejé las galletas en la mesa de la cocina.
Cuando Clara hubo salido, doña Margarita tomó el anuncio de la conferencia, y leyó:
La Sociedad de los Amigos, capítulo de Lancaster
anuncia lo charla
"Los pesos relativos de los átomos"
por el señor
JUAN DALTON
del Instituto Real de Manchester.
15 de junio de 1807
—!Esta hija mía! —murmuró para sí preocupada doña Margarita—.
—No sé que le ve a este hijo de mi difunta prima. Parece que es listo, eso dicen, muy buena persona, seguidor muy fiel de las ideas de nuestro fundador Jorge Fox; dicen que jamás falla al servicio religioso los domingos, pero es muy rústico y la franca verdad no es nada apuesto. Sí, sí, soy frívola, no debiera pensar así, pero de todas maneras no creo que a base de clases particulares de química y física y menos con sus ideas de átomos pueda sostener una familia. ñátomos, bah! Dios me perdone, pero preferiría que fuese menos listo y más realista.
El salón de actos estaba atestado de gente; en aquellos años, todos se sentían científicos, esto es, se interesaban por la Naturaleza en forma racional y se sentían con derecho a emitir toda dase de opiniones al respecto. Un anuncio de una conferencia científica era garantía de un lleno completo. Cuando el conferencista avanzó al estrado y empezó a hablar, la decepción del público fue palpable. Ciertamente, Juan Dalton no era un brillante expositor, su voz era baja y monótona, y sus pantalones a la rodilla, con botones, sus medias grises y sus zapatos de hebilla, en el más puro estilo cuáquero, no eran para entusiasmar. Pero Clara era simplemente ciega y sorda a todo aburrimiento y en su persona sólo había lugar para una profunda atención a lo que Dalton decía y para una suprema admiración por su inteligencia.
—...se ha establecido pues más allá de toda duda razonable, la verdad de las proporciones constantes, pero todos sabemos que la materia, aunque divisible en grado extremo, sin embargo no es infinitamente divisible. Es decir, debe haber cierto punto más allá del cual no es dado al hombre subdividirla.
Un joven levantó la mano y dijo:
—¿Tiene usted un argumento químico a favor de la hipótesis de partículas indestructibles o únicamente este argumento de imposibilidad o de sentido común?
—Permítame que le conteste con una pregunta. Si la materia fuese infinitamente divisible y en vista de la fuerte afinidad a reaccionar que presentan el hidrógeno y el oxígeno, tanta que hasta lo hacen explosivamente, ¿por qué no se combinan entre sí en todas proporciones?
El preguntón levantó las manos en gesto de impotencia en medio de murmullos de regocijo y Dalton continuó:
—Así pues, tenemos dos datos, ley de proporciones constantes que ya he elaborado bastante y teoría de partículas últimas. Ahora elaboraré ésta de la manera más sencilla posible.
—Consideren sus mercedes los siguientes postulados:
a) La materia consiste de partículas últimas, formadas por un centro duro muy pequeño rodeado de una envoltura de calórico, como lo supuso el gran Lavoisier que en paz descanse. —Y Dalton mostró una borla de estambre que en su centro tenía un botón—. Más o menos así.
b) Cuando las substancias son simples, es decir elementos, sus partículas últimas son todas iguales entre sí, mismo tamaño incluyendo su envoltura calórica y mismo peso. No se puede distinguir una de otra en un elemento puro. Llamaré —continuó— átomos a estas partículas últimas. El diámetro y el peso de los átomos de cada substancia elemental son diferentes de los de cualquier otra substancia elemental y no hay dos elementos que tengan sus átomos iguales, pero en todos los elementos, los átomos son globulares borlas redondas un tanto tiesas. Ningún poder que podamos controlar nos permite cambiar átomos de un elemento en los de otro; así que la transmutación alquímica es imposible, como lo ha probado la historia de su fracaso.
c) Los átomos de las substancias compuestas son átomos compuestos que están constituidos de los átomos sencillos de los elementos. Para que no haya confusión, llamaré a los átomos compuestos moléculas. Las moléculas se pueden armar y desarmar. Cuando esto último ocurre, la substancia en cuestión deja de ser lo que es. Todas las moléculas de una substancia pura son idénticas en tamaño y peso. Las moléculas son redondas, o si prefieren, globulares, los centros de los átomos que se combinan se mantienen en contacto por una fuerte afinidad rodeados de una envoltura común de calórico.—Al llegar a este punto, Dalton mostró al auditorio un par de borlas unidas por sus botones centrales, y continuó:
d) En las reacciones químicas, los átomos únicamente se rearreglan, no se crean ni se destruyen. El análisis y síntesis químicas no van más allá de la separación de partículas unas de otras y de su reunión. No hay creación ni destrucción de materia al alcance de los agentes químicos.
—Tanto valdría como querer introducir un nuevo planeta en el Sistema Solar; o como querer aniquilar uno ya existente, querer crear o destruir un átomo de hidrógeno. Todos los cambios químicos que podemos producir; consisten en separar partículas que están en estado de cohesión o combinación, y unir aquellas que estaban previamente a distancia. Como sus mercedes pueden apreciar, esta simpleza explica la conservación de la masa que Lavoisier postuló y demostró experimentalmente, hace décadas.
—Es muy latoso dibujar la envoltura de calórico y para podernos entender
con facilidad, propongo que usemos los siguientes esquemas, meros símbolos —al
llegar aquí, Dalton procedió a mostrar de uno en uno, distintos discos de madera
que fue sacando de una caja. Tenían el siguiente aspecto:1![[Nota 1]](../img/mcommnt.gif){kind=small}
Los discos circularon entre los presentes, algunos los tomaban en sus manos con tal reverencia como si estuvieran recibiendo los mismísimos átomos; otros, menos imaginativos y quizá por lo mismo menos inteligentes, simplemente los pasaban a sus vecinos con perezoso desdén.
—Ahora, apreciables oyentes —continuó Dalton—, se impone una primera conclusión, a saber, una proporción fija en peso implica una proporción fija en número de átomos constituyentes. Esto, creo, es de la mayor importancia.
Al ver que la mayoría de sus oyentes se le quedaba mirando con ojos vacíos de toda comprensión, precisó: —Al formarse moléculas en una reacción química, los números de los átomos que se combinan de los diferentes elementos lo hacen en proporciones fijas.
Quizá convenga poner ahora un ejemplo. Sean la substancia A que tienen tendencia a combinarse con la substancia B para formar un compuesto cuya molécula de alguna manera sabemos está formada por un átomo de A de masa ma y dos de B, cada uno de masa mb. Supongamos que ponemos seis átomos de A a reaccionar con ocho de B:
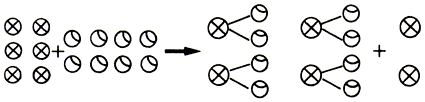
vemos que la masa de cada una de las moléculas será de ma+2mb y que sobran dos átomos de A.
Pero ¿cómo deducir el peso relativo de los átomos? Hay un pequeño detalle y es que a diferencia del ejemplo, no tenemos manera de saber cuántos átomos de cada elemento participante intervienen en una molécula. Pongamos un ejemplo, el agua, sabemos que es una combinación de hidrógeno con oxígeno en proporción de 1/8 en peso; esto es, denotando el peso por P,
—Ahora bien, en una molécula de agua, ¿entra un átomo de hidrógeno por uno de oxígeno, o dos por uno, o al revés? Si suponemos lo más sencillo, que es uno a uno, entonces, si denotamos el número de átomos por N, NH/NO =1/1 y como PH = NH x wH y PO = N0 x wO, en donde he designado el peso de un átomo de hidrógeno por wH y el peso de un átomo de oxígeno por wO, se tiene que
en palabras, un átomo de oxígeno pesaría, relativamente a uno de hidrógeno, ocho tantos.
—Pero si suponemos que entran dos de hidrógeno por uno de oxígeno, entonces, NH/NO =2/1 y tendríamos que,
en palabras, concluiríamos que un átomo de oxígeno es 16 veces más pesado que uno de hidrógeno. Así, proporción fija en peso implica proporción entre los pesos de los átomos participantes. La fórmula de la mayor utilidad que emplearé es
Vemos que para pasar del dato de laboratorio, Px/Pz, a la incógnita Wx/Wz, se necesita decir algo sobre Nx/Nz. Ante esta situación, tomemos la regla de la mayor simplicidad:
—Cuando sólo una combinación de dos elementos A y B se puede
obtener, deberá suponerse, a menos de tener indicaciones de lo contrario, que
ésta es una molécula binaria. Así, escribimos las siguientes combinaciones,
agua, gas nitroso etc. Pero la combinación de dos elementos no siempre produce
un solo compuesto;2 cuando
dos combinaciones se observan, deberá presumirse una de ellas una molécula binaria
y la otra molécula ternaria, por ejemplo óxido carbónico y ácido carbónico,
etcétera.3
En ese momento el joven H. Davy levantó la mano pidiendo la palabra.
—Me parece —dijo levantándose—, que hasta este momento su hipótesis atómica da una fundamentación física a la ley de las proporciones fijas muy atractiva y probablemente correcta, pero de ninguna manera es una prueba de la existencia de los átomos.
—Y no lo pretendo yo. Sin embargo, el caso a favor de la hipótesis atómica cuenta con un argumento más fuerte a su favor del hasta ahora expuesto si me permite continuar...
—ñAdelante, desde luego! —apresuró a contestar.
—Cuando dos elementos A y B, se combinan para formar dos compuestos diferentes, los pesos de B en los dos compuestos, combinados con un peso dado de A, están en una proporción de números enteros. Llamo a esta regla que deben obedecer las varias proporciones fijas cuando se dan, regla de las proporciones múltiples. Por ejemplo, los últimos datos informados sobre los dos gases compuestos de carbón y oxígeno son los siguientes:
| óxido carbónico: 1.00 g de | se combinan con 1.34 g. de |
| ácido carbónico: 1.00 g | de se combinan con 2.67g. de |
—De aquí vemos que las cantidades de oxígeno combinado con una cantidad fija de carbón dan la proporción 2.67/1.34 o 1.9925/1, redondeando por el error experimental, 2/1 es la relación de números enteros más cercana. En esta tabla 1, les muestro algunos ejemplos:
—Espero que sea claro, estimados oyentes, que la regla de proporciones
múltiples que exhibe esta tabla, obtenida experimentalmente, se explica, casi
trivialmente, con la hipótesis atómica, pues que nos dice la última columna
es que el cociente entre el número de átomos de oxígeno en el compuesto del
primer renglón al número de átomos de oxígeno en el compuesto del segundo renglón,
en cada caso es un cociente de números enteros, como debe de ser dado que los
átomos son indivisibles.4 Creo
que si bien no he presentado una demostración directa de la existencia de los
átomos, sí he explicado un resultado experimental y universal con la hipótesis
atómica y he hecho a ésta plausible. Muchas gracias.
Los aplausos fueron nutridos. El presidente de la Sociedad de los Amigos se levantó para iniciar las preguntas.
—¿Podría mostrarnos un ejemplo práctico de aplicación del conocimiento de los pesos atómicos relativos? —preguntó—.
— Sí, desde luego —contesto Dalton—. ñYa se me olvidaba! Primero
vean esta tabla de pesos atómicos que he compilado tomando el peso de un átomo
de hidrógeno como 1.5
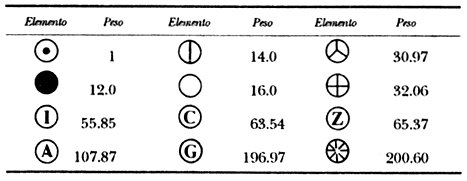
Supónganse que se encuentran con un óxido de hierro de fórmula desconocida pero cuya composición en peso es 70.0% de hierro y 30.0% de oxígeno. Como ya dije,
de la tabla anterior obtengo cuánto vale WFE/wO, vale 56/16. Substituyendo ahora este valor arriba obtengo que:
que no es sino 0.6667, o 2/3, es decir; el compuesto en cuestión contiene dos átomos de hierro por cada tres de oxígeno y por lo tanto su fórmula será I 2 O3.
Cuando ya habían salido la mayoría de los asistentes, varios jóvenes se acercaron a Dalton a pedirle que les aclarara la afirmación sobre el significado de la última columna de la tabla 1.
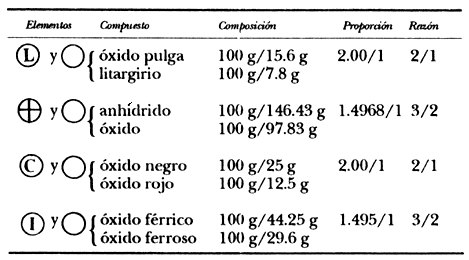
—Sí, miren. Para el óxido pulga, Pp/PO= 6.4103 y
Ahora despejo de aquí el cociente de pesos atómicos
En donde NO representa el número de átomos de oxígeno en el óxido pulga. Noten que para el litargirio, el peso del plomo es el mismo, Pp/pO=12.8205 y
En donde no representa el número de átomos de oxígeno en el litagirio. Sustituyo ahora el cociente de pesos atómicos de esta segunda relación en la anterior y obtengo:
—Pero existen casos más complicados, por ejemplo, los diversos compuestos entre oxígeno y nitrógeno...
—Sí, mira esta tabla, construida con la regla de la mayor simplicidad.
|
|
|||||
|
Substancia
|
Apariencia
|
Densidad 6
|
%
|
%
|
Razón
|
|
gas nitroso
|
incoloro
|
1.03
|
46.7
|
53.2
|
1/1
|
|
óxido nitroso
|
incoloro
|
1.52
|
63.6
|
36.4
|
2/1
|
|
anh. nítrico
|
café rojizo
|
1.59
|
30.4
|
69.6
|
1/2
|
|
anh. nitroso
|
café rojizo
|
2.62
|
36.9
|
63.1
|
2/3
|
|
|
|||||
A partir de ella pueden comprobar que el cociente entre las razones cualesquiera dos de estos compuestos es un número entero.
—Sí, pero en realidad las razones de la última columna no son exactas...
—ñNo importa! Resultan aproximadas por el error experimental inevitable pero de hecho son exactas.
Tomados del brazo, Dalton y Clara caminaron en silencio por la orilla del río, bajo la sombra de los árboles. Clara le comentó,
—Oyéndote me acordé de los átomos de Demócrito...
—ñNo, Clara! Los átomos son muy diferentes a como los imaginó Demócrito. Él los supuso en perpetuo movimiento, con amplio espacio vacío entre ellos. La verdad es que están en quietud y contiguos unos con los otros.
—¿Y cómo sabes que están estáticos?
—ñAh! Porque el gran Newton dedujo la ley de Boyle, la que dice que la
presión a la que está confinado un gas es proporcional a su densidad. La deducción
la hizo suponiéndolos estáticos y repeliéndose entre sí, de acuerdo con una
fuerza que va como el inverso del cuadrado de la distancia entre sus centros.7
Esto,
me parece, es más que suficiente; sin embargo, añadiré que tu humilde servidor
ha podido comprender cómo es que la mezcla que llamamos aire no se separa en
capas de nitrógeno y de oxígeno, que tienen densidad diferente, como ocurre
en una mezcla de aceite y agua, y que lo ha comprendido gracias a las hipótesis
de que los átomos de uno y otro gas tienen tamaño diferente, de que están contiguos,
de que se repelen los de una misma clase como Newton estableció, pero como si
los de la otra clase no estuvieran presentes y de que están estáticos.
— Entonces dijo Clara con voz soñadora—, el aire es una mezcla homogénea porque es una apilamiento de borlas de dos clases, revueltas, ¿cómo puede ser esto?
—Es algo complicado, nos tomaría mucho tiempo discutirlo, es asunto de la estabilidad de la mezcla y mira, ya llegamos a tu casa y mi tía ya nos divisó por la ventana.
Ya sentados ante el servicio de té, cuando doña Margarita vio que Dalton había hecho los honores a las galletas y mientras le servía una segunda taza de té, le comentó:
—Así que la conferencia fue todo un éxito.
—No crea tía, pienso que la mitad del auditorio se aburrió.
—¿Pues que no es muy interesante el asunto de los átomos?
—ñOh, sí! —Al decir esto, el rostro de Dalton se iluminó y por extraño que parezca, por unos instantes se vio hermoso—.
—Pues entonces, ¿qué sucedió? —preguntó Margarita, que no conocía la discreción y menos tratándose de un probable yerno. Clara, sin levantar la vista, simplemente se alisó el vestido—.
—Es que mi idea es demasiado sencilla, no es espectacular.
—ñCómo puedes decir que es sencilla, Juan! —intervino Clara—.
—Sí, mira. En química ocurre como cada vez que se pelan chícharos, el peso de los chícharos es al peso de las vainas un número constante. Concluyes que hay un número de chícharos por vaina, ¿no? Aunque no sepas cuántos.
Como Clara se sonriera, Dalton continuó animado.
—Ahora imagínate que hay varias especies de chícharos, de modo que en una especie encuentras una proporción fija de chícharos a vaina y en las otras, otras proporciones. Como sólo puede haber un número entero de chícharos por vaina, el cociente del número de chícharos por vaina en una especie al número de chícharos por vaina en otra, tendrá que ser un cociente de números enteros...
—Y luego —continuó Clara—, para una especie, habiendo supuesto un número de chícharos por vaina, puedo saber cuál es el peso relativo de un chícharo respecto de una vaina.
—Que tú lo expliques en términos sencillos no quiere decir que no sea genial, a nadie de los grandes profesores se le había ocurrido, y todos han tenido los datos del caso enfrente.
Dalton se ruborizó y doña Margarita sintió ganas de matar a Clara. ñQue encima de todo lo alentara en sus locuras...! Así que intervino un tanto agriamente.
—Supongo que con tus clases y con tus brillantes ideas, te estarás labrando una posición y pronto nos darás la noticia de tu matrimonio.
—ñOh no, tía, como le he escrito a mi hermano, el matrimonio es un lujo para mí que nunca me daré!
Regresemos ahora a París, a la Societé Philomathic el día último del año de 1808. En el vestíbulo del salón de actos numerosos investigadores se preparan a escuchar la memoria titulada "Sobre la combinación de substancias gaseosas unas con otras" por José Luis Gay-Lussac, de la Sorbona. Por tratarse de la última conferencia del año, se ha servido vino y bocadillos antes de dar comienzo a la sesión; hay un ambiente festivo porque a todos aguarda después una buena cena con amigos, para despedir el año.
Entre el rumor de los brindis y las manifestaciones de buenos deseos, se oyen comentarios:
—Tengo entendido que Gay-Lussac es un colaborador del maestro Berthollet.
—Más que un colaborador; es uno de sus alumnos más distinguidos y bastante independiente. El trabajo que hoy nos va a presentar lo inició hace cuatro años en colaboración con el barón Alexander von Humboldt.
—Sí, y me parece —terció otro— que lo inició porque se fascinó con lo que llama la "bellísima simplicidad" de los resultados de Cavendish con la síntesis del agua. Ha aplicado el método de hacer reaccionar gases, mediante el expediente de hacer saltar chispas eléctricas, a toda suerte de mezclas.
—Una medida del aprecio que le tiene Berthollet es que lo deja seguir su propia línea en su laboratorio.
—Sobre todo porque estas investigaciones sobre gases las ha llevado a cabo por "el puro amor al arte"; no pertenecen directamente a ningún proyecto relacionado con la industria, ni a ningún fin práctico inmediato.
—Sorprendente sabiendo que es miembro del Comité Consultor de Artes y Manufacturas.
—¿Saben que Gay-Lussac está recién casado?
—Sí, y las circunstancias de su elección de esposa han dado la vuelta por todo París...
—Al entrar a una tienda de blancos vio a una de las empleadas leyendo un libro... ñDe química! Inmediatamente la cortejó, se casó y está reforzando su educación... ñLa tiene aprendiendo inglés e italiano!
En ese momento, el organizador de los seminarios comenzó a dar fuertes palmadas para congregar al auditorio.
Comenzó explicando lo esencial de sus experimentos: hacer reaccionar volúmenes iguales de diversos gases, previamente medidos bajo las mismas condiciones de presión y temperatura. Determinar los volúmenes tanto de los productos como de los reactivos no consumidos, desde luego a la misma temperatura y presión, restar los volúmenes de los reactivos sobrantes de los volúmenes iniciales empleados para obtener el volumen de cada uno que en verdad reaccionó. Después de describir el equipo, exhibir los pasos de sus cálculos y subrayar que en todos los casos investigados se había mantenido la temperatura lo suficientemente alta para garantizar que tanto los reactivos como los productos de la reacción permanecieran en fase gaseosa, Gay-Lussac hizo un resumen de sus hallazgos.
—Después de redondear las cifras de los cálculos con un error en la determinación de los volúmenes de 0.1%, podemos establecer lo siguiente. En el caso del agua ocurre para los volúmenes combinantes que:
|
o o
|
+
|
o |
=
|
o o
|
|
2 volúmenes de hidrógeno
|
+
|
1 volumen de oxígeno
|
=
|
2 volúmenes de vapor de agua
|
en el caso de los óxidos de carbono, otro tanto:
|
o o
|
+
|
o
|
=
|
o o
|
|
2 volúmenes de óxido carbónico
|
+
|
1 volumen de oxígeno
|
=
|
2 volúmenes de anh. carbónico
|
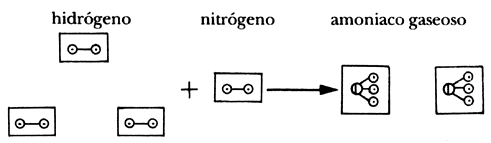
en el caso del amoniaco los resultados indican:
|
o
|
+
|
o o o
|
=
|
o o
|
|
1 volúmen de nitrógeno
|
+
|
3 volúmenes de hidrógeno
|
=
|
2 volúmenes de amoniaco
|
en el caso de la fosfina, obtuvimos:
|
o o o
|
||||
|
o
|
+
|
o o o
|
=
|
o o o o
|
|
1 volúmen de fósforo
|
+
|
6 volúmenes de hidrógeno
|
=
|
4 volúmenes de fosfina
|
—La conclusión inescapable, caballeros, es que cuando se unen gases para formar nuevos compuestos, los volúmenes de los reactivos consumidos y los de los productos están en una relación de números enteros.
Dos estudiantes se quedaron en el vestíbulo desierto de la Sociedad Philomathica; el anciano conserje, escoba en mano, veía sus cabezas inclinadas sobre un cuaderno, los oía discutir; era día último del año, afuera hacía un frío de perros. Regresaría a cerrar después de la cena.
—A ver, otra vez. No entiendo por qué dices que Dalton jamás aceptará los resultados de Gay-Lussac —estaba diciendo uno de los estudiantes cuando el viejo salió.
—En resumen, las características relevantes del modelo de Dalton frente a los resultados informados por Gay-Lussac son que los átomos tienen tamaño, que están contiguos, y que los de distintos elementos son de tamaño distinto. En consecuencia, dado un volumen, un centímetro cúbico, por ejemplo, contendrá un número diferente de átomos según el elemento químico que sea y viceversa, un número dado de átomos ocupará un volumen diferente según el elemento de que se trate.
—ñAjá!, para Dalton, volúmenes iguales de diferentes gases no pueden contener número igual de átomos.
—Ahora bien, Félix, toma el caso del gas nitroso. Dalton, que según los chismes es pésimo experimentador, encuentra que se combinan en una proporción fija un volumen de nitrógeno con algo menos que un volumen de oxígeno; para él esta discrepancia está llena de significado, puesto que, para él, los átomos de distintos elementos son necesariamente de tamaño diferente, y como por su regla de máxima simplicidad se combinan uno a uno, sus volúmenes combinantes, que cada uno llena totalmente, no pueden ser iguales. Gay-Lussac, reconocido como un experimental de primera, encuentra que los volúmenes combinantes de los reactivos, con un error experimental inevitable, muy pequeño, son prácticamente idénticos; redondea los resultados y concluye que la relación de volúmenes es una relación de números enteros. ñEs este redondeo lo que Dalton no acepta! Y sin embargo, redondear es lo que hizo en el caso de las proporciones fijas en peso. Para Dalton el experimento es:
Mientras que para Gay-Lussac, el experimento es:
—Hmmmf, ya veo. Para uno el error experimental inevitable es la manifestación de una importante verdad, y para el otro, un dato despreciable. O sea, esencialmente cuestión de interpretación...
— Así es; pero Dalton es "parte interesada". Él querrá a toda costa sostener que el tamaño atómico es diferente en cada elemento químico, porque ha fundamentado su explicación de la homogeneidad de la atmósfera en varias hipótesis, entre las cuales la de que el tamaño es importante, y no ha de querer renunciar al modelo que le sirvió.
—Bueno, pero el asunto del tamaño de los átomos no interviene para nada en la validez de su interpretación atómica de la ley de las proporciones múltiples.
—ñClaro! Ésa es la belleza de la ciencia, en su progreso como en la vida, van juntos "el trigo con la cizaña" y nunca nada es totalmente la última palabra. También podemos decir que para Dalton, la ecuación del experimento, a saber, un volumen de nitrógeno más un volumen de oxígeno igual a dos volúmenes de gas nitroso significa: un átomo se une con un átomo para dar una molécula del doble de grande, aproximadamente.
—Bueno, y ¿qué hay respecto del otro modelo de los gases? ¿Te acuerdas? Ya desde mediados del siglo pasado, Daniel Bernoulli sugirió que a presión y temperatura constantes, volúmenes iguales de gases pudieran contener igual número de partículas porque simplemente aunque tuvieran tamaños diferentes son tan pequeñísimas con respecto al volumen que "invaden" que sus diferencias de tamaño no importarían. En este caso se podría interpretar el resultado de Gay-Lussac en forma análoga a como interpretó las proporciones fijas en peso Dalton; es decir; así como él dijo en esencia, que el peso es proporcional al número de átomos, así, tomar los resultados de Gay-Lussac como proporciones fijas en volumen y decir que el volumen es proporcional al número de partículas; a igualdad de presión y temperatura, ñclaro!
—ñAh, sí! Pero en el modelo de Bernoulli los átomos están en movimiento, por eso a pesar de ser pequeñísimos invaden un volumen muy grande, y eso Dalton no lo acepta, porque se le viene abajo su demostración de la homogeneidad de la atmósfera basada en átomos quietos.
—No se vale. ¿Cómo es entonces un científico tan grande?
—Te voy a decir cómo. Frente al hecho experimental,
Dalton te preguntaría si volúmenes iguales contienen iguales números de partículas, entonces el doble de volumen contiene el doble de partículas. ¿De acuerdo? ¿Cómo puede un átomo de nitrógeno combinarse con uno de oxígeno para formar dos moléculas de gas nitroso? ñA ver! Y no sólo esto. Dalton te diría, toma el caso del agua, supónte por simplicidad dos átomos de hidrógeno OO en el volumen doble de hidrógeno y un átomo de oxígeno O en el volumen sencillo de oxígeno, ¿cómo es posible obtener dos moléculas OO sin dividir al átomo de oxígeno? ñAh! En cambio yo, te diría Dalton, pienso que en los dos volúmenes de hidrógeno hay el mismo número de átomos que en el volumen de oxígeno.
—¿Quién tiene razón? —preguntó abrumado Félix sujetándose la cabeza con los codos sobre la mesa—. ¿Dalton, quien dice que no se vale redondear el resultado experimental, o los que dicen que sí se vale? ¿Dalton, o los que afirman que a igualdad de presión y temperatura, volúmenes iguales de gases diferentes contienen igual número de partículas?
—Primero habría que pulir el experimento hasta convencerse si el error experimental disminuye o permanece. Después, si disminuye, que es lo que yo creo, habrá que encontrar la respuesta a las objeciones de Dalton.
—En cuanto regrese a Turín le preguntaré a mi maestro Avogadro...
En ese momento regresó el conserje.
—Lo siento muchachos, pero no se pueden quedar ya más aquí, tengo que cerrar.
— Está bien. Gracias abuelo y ñfeliz Año Nuevo 1809.
El profesor turinense Lorenzo Romano Amadeo Carlo Avogadro di Quaregna e di Cerreto, aceptó los datos de Gay-Lussac y su redondeo, el tiempo le dio la razón, y propuso en 1811 un modelo para los gases que empató uno con otro los trabajos de Dalton y de Gay-Lussac. Su modelo incorpora ideas que habían estado flotando en el ambiente, con contribuciones propias. Se puede expresar en los tres enunciados siguientes.
i) Las partículas últimas no están en contacto permanente, tienen capas muy sutiles de calórico y sus dimensiones son despreciables comparadas con las distancias que las separan.
En consecuencia, volúmenes iguales de todos los gases, ya sean elementos, compuestos o mezclas, en igualdad de temperatura y presión, contienen igual número de partículas.
ii) Las partículas últimas de los elementos químicos no tienen por qué consistir de un solo átomo. Se puede concebir perfectamente que las partículas últimas de un elemento químico gaseoso sean moléculas de varios átomos iguales.
El incremento de tamaño que esto implica es de todos modos despreciable frente a las distancias entre las partículas.
iii) No tenemos por qué suponer que cuando las moléculas de los elementos se unen para formar un compuesto, hayan de permanecer en un agregado mayor. Es posible concebir que agregados voluminosos se fragmenten inmediatamente en moléculas iguales del compuesto.
Para apreciar la belleza y el ingenio de la teoría de Avogadro, considérense los siguientes casos particulares.
El agua, de acuerdo con los enunciados (i) y (ii) puede formarse
por las siguientes posibilidades:8
| 1) | H | + | O | ® | HO | la propuesta por Dalton. | |
| 2) | 2H | + | O | ® | H2O | la admitiría Dalton. | |
| 3) | H2 | + | O | ® | H2O | hidrógeno diatómico. | |
| 4) | 2H | + | O2 | ® | [H2O2] | ® | 2H2O, oxígeno diatómico |
| 5) | H2 | + | O2 | ® | [H2O2] | ® | 2HO, |
| 6) | 2H2 | + | O2 | ® | [H4O2] | ® | 2H2O, |
| 7) | 2H3 | + | O2 | ® | [H6O2] | ® | 2H3O, etcétera |
De acuerdo con el enunciado i), debemos dibujar el mismo número de moléculas en todos los cuadrados de Gay-Lussac que simbolizan el volumen. Un instante de reflexión nos muestra que es imposible hacerlo suponiendo las situaciones (1), (2) y (3) sin dividir átomos. La posibilidad (5) es imposible también porque el experimento requiere que se combinen dos volúmenes de hidrógeno. En cambio es perfectamente posible satisfacer (i) suponiendo (4), o (6) o (7) u otras posibilidades. ¿Cómo reducir el número de posibilidades? Pues viendo cuáles se permiten en otras reacciones en las que intervenga uno de los dos gases. Considérese ahora el caso del amoniaco: tres vols. hidrógeno + un vol. nitrógeno = 2 vols. amoniaco. Reflexión y ensayo y error no hace ver que este resultado experimental exige que el hidrógeno sea diatómico porque entonces:
Así pues, queda descartada la posibilidad de que el hidrógeno sea monatómico, lo que descarta, para el vapor de agua, la posibilidad (4). Al llegar aquí, Avogadro utiliza una regla de simplicidad para escoger la alternativa (6) como la correcta. Pero esta regla, a diferencia de la de Dalton, no conduce a conflictos, porque se invoca para elegir entre posibilidades que ya satisfacen al experimento y al modelo. Hemos podido por lo tanto establecer la fórmula del agua común.
Notamos que de acuerdo con el primer postulado de Avogadro el número de moléculas de agua que se forma es igual al número de moléculas de hidrógeno que se consume porque los volúmenes de vapor y de hidrógeno son iguales. Notamos también que se forman como máximo tantas moléculas de agua como átomos hay en la molécula del oxígeno, que es el gas que entra con el volumen unitario. Esto último nos ayuda a establecer la fórmula del fósforo gaseoso, y de la fosfina. Leyendo la expresión del experimento concluimos que la molécula de fósforo gaseoso debe contener cuatro átomos de fósforo. La fórmula de la fosfina se puede establecer ahora de inmediato, tiene un átomo de fósforo, y ya sabemos de los anteriores experimentos que el hidrógeno es diatómico. Puesto que seis volúmenes de hidrógeno se requieren para producir cuatro de fosfina, entonces se requieren seis moléculas de hidrógeno para producir cuatro de fosfina o lo que es lo mismo se requieren 12 átomos de hidrógeno para producir cuatro moléculas de fosfina. Por lo tanto, en cada una hay 12/4 = 3 átomos de hidrógeno. Y la fórmula de la fosfina es PH3.
Los experimentos de Gay-Lussac y la aceptación de los postulados de Avogadro nos proporcionan un método para determinar la fórmula molecular de cualquier elemento o compuesto que pueda ser obtenido en el estado gaseoso a temperaturas accesibles en el laboratorio. Con esto se hace totalmente innecesaria la regla de la mayor simplicidad que Dalton tenía que invocar. En la expresión (f) empleada por Dalton, ahora el cociente Nx/Nz puede ser conocido y la expresión usada, junto con las proporciones, fijas en peso experimentales, para establecer una tabla de pesos atómicos relativos. En la actualidad, las tablas de pesos atómicos están referidas ya no al átomo de hidrógeno sino al de carbono, fijado por acuerdo internacional con el peso 12.
El modelo de los gases de Avogadro no fue aceptado de inmediato por diversas razones, entre otras porque era poco conocido su trabajo y pasó inadvertido por casi 50 años, baste decir que en 1814 Ampñre propuso un modelo semejante y fue mucho después cuando salió a relucir el de Avogadro. Más tarde, el comportamiento del mercurio y del azufre gaseosos, cuyas moléculas no son binarias (en su modelo original, Avogadro sólo consideraba este caso) pareció echarlo por tierra. Actualmente, su modelo se considera correcto.
Nos encontramos en el primer cuarto del siglo XIX, en plena infancia de la química clásica; no juventud todavía, pues aún anda desfilando con bandera de substancia el calor. Niña, pero ya es una ciencia y previsiblemente, más que agotarse las preguntas, ahora se multiplican. Ya la meta de este viaje ha sido alcanzada: la tecnicolorida alquimia, con honor (nunca hay que despreciar los esfuerzos) ocupa su vitrina en el museo de los trofeos de guerra intelectual y los átomos son casi palpables; pero sólo para nosotros, los que estamos río abajo en el tiempo. No se engañe el lector; para muchos científicos a lo largo del siglo XIX, los átomos y las moléculas no pasaron de ser un figmento de la imaginación, al cual prestaban acaso, condescendientemente, un valor de ayuda pictórica, propia de mentes con debilidades de geometría. A esto contribuyó no poco la falla grave en el modelo de Dalton de la contigñidad de los átomos, que llevaba a contradicciones con los experimentos, permaneciendo la contribución de Avogadro en la oscuridad. La aceptación final de la existencia de las moléculas y de los átomos no se obtendrá sino hasta la interpretación de Einstein del movimiento browniano, en 1905.
Hablando de preguntas, son innumerables. Algunas pocas inmediatas se han quedado esperando, las que estoy segura, a más de un lector le bullen en la cabeza. Es apropiado mencionarlas porque con este viaje se quería "vivir" la ciencia, y ésta es un asunto de nunca acabar. ¿Si pueden existir fuerzas de atracción entre átomos iguales para formar moléculas de los elementos, por qué no causan que todo el gas se condense en una molécula gigante? ¿Por qué es estable una molécula de agua, o de nitrógeno? ¿Por qué no todas son binarias y hay moléculas como P4, S2, S6, S8? ¿Por qué están los átomos en las moléculas de los compuestos en ésas proporciones particulares y no en otras? Las respuestas a estas preguntas han sido dadas sólo en las últimas décadas de este siglo gracias a la mecánica cuántica, teoría moderna que se ocupa de la estructura de los átomos y las moléculas y de la matematización de las cualidades de las substancias.
![[Inicio]](../img/begin.gif)
