IV. LA DINÁMICA DE LOS GENES

CONSIDEREMOS el problema que preocupó a Reginald C. Punnet (1873-1951) a principios de siglo. Si tenemos genes dominantes y recesivos para el color de los ojos, el gene que determina el color oscuro es dominante sobre el que determina el color de ojos claro. Así un individuo que tenga los dos genes, uno heredado de su madre y el otro de su padre, tendrá ojos oscuros. Un hombre de ojos claros casado con una mujer de ojos oscuros homóciga tendrán hijos o hijas con ojos oscuros por este efecto de dominancia. Punnett entonces se preguntaba, ¿que pasará dentro de varias generaciones, en este mundo donde la comunicación está poniendo en contacto cada vez más a personas de muy diversos orígenes? Punnett pensaba que con el tiempo, la mayor parte de la población tendría un color oscuro de ojos por el efecto de la dominancia.

DEL ENTRETENIMIENTO DE HARDY

Punnet tenía un amigo matemático, Godfrey H. Hardy (1877-1947) al que le planteó su problema y Hardy, después de hacer una cuenta sencilla le dijo que no ocurriría lo que Punnett creía. Que si se juntaran dos poblaciones puras para ojos claros y ojos oscuros en proporciones iguales y los individuos se aparearan al azar (lo cual definitivamente no está ocurriendo) en una generación tendríamos tres cuartas partes de la población con ojos oscuros y una cuarta parte con ojos claros. No es que los genes originales claros se pierdan sino que por el efecto de la dominancia, la mitad de ellos se encuentran en individuos heterocigotos dominados por genes de ojos oscuros y que las frecuencias de los genes no cambiarían de una generación a otra. De hecho, y este es el resultado más importante, Hardy podía predecir a partir de las frecuencias de los diferentes genes las frecuencias de los genotipos que habría en la población bajo ciertas condiciones de apareamiento y la ausencia de otras, como la selección natural, la mutación, la deriva génica y la migración, que veremos posteriormente.

Es decir, de las frecuencias génicas p y q de los alelos A₁ y A₂ se pueden predecir las frecuencias de los tres genotipos A₁A₁, A₁A₂ y A₂A₂ como pñ, ₂pq y q₂. Si las frecuencias génicas son, digamos, 0.7 y 0.3 para cada uno de los dos alelos, las frecuencias genotípicas serán 0.49, 0.42 y 0.09 para cada uno de los tres genotipos. Habrá, por ejemplo, 49% de los individuos con el genotipo A₁A₁. Si la población tiene 324 individuos, de ellos alrededor de 159 tendrán ese genotipo.

Este sencillo principio, forma la base de todo lo que actualmente conocemos sobre la dinámica de los genes. Considerando una población en la que no existe selección natural, de tamaño infinito (sin deriva génica), sin mutación, sin migración y donde los apareamientos son al azar entre los individuos, las frecuencias génicas no cambian de generación en generación y las frecuencias genotípicas pueden ser predichas como una expansión del binomio (p+q)ñ. Otras suposiciones que no son obvias son, por ejemplo, que la población sea diploide, que las frecuencias alélicas sean iguales en machos y hembras, y que los genes no estén ligados al sexo, es decir, no estén en los cromosomas sexuales.

LA VIDA DE WEINBERG

Los antecedentes de Wilhelm Weinberg (1862-1937) fueron completamente diferentes de los de Hardy. Siendo médico de profesión, sus preocupaciones durante toda su vida giraron alrededor de la genética de poblaciones humanas en particular, y de la evolución de las características en los organismos en general. No sólo describió en forma independiente pero simultánea (1908), los mismos principios que Hardy sino que además estudió la evolución de características cuantitativas, adelantándose una década a los descubrimientos que en este campo haría Ronald Fisher en 1918. La expansión del binomio propuesta por Hardy y Weinberg se ha llamado la ley de Hardy Weinberg y como es el caso en algunos fenómenos de la ciencia, la ley no es válida más que en poblaciones en donde no hay selección, deriva génica, mutación, migración y en las que el apareamiento es al azar. Estas poblaciones, como es de suponer, no existen, por lo que la ley funciona solamente en aquellos casos en los que no se cumpla la selección, que probablemente será la mayoría de las poblaciones naturales. El otro aspecto interesante de la ley es que al ser llamada de Hardy Weinberg, es probable que no se reconociera a Weinberg como el verdadero genetista, pues en realidad debiera llamarse el principio de Weinberg-Hardy.

De hecho, el artículo de Weinberg, en alemán, se publicó seis meses antes que el de Hardy, pero por varios años el principio fue llamado la ley de Hardy. Por otro lado, como ya se ha mencionado, Weinberg era un genetista e hizo otras contribuciones a la genética de poblaciones, como ampliar el principio de Hardy-Weinberg a un gene con más de dos alelos. Asimismo, estudió el principio para más de un gene, encontrando, por ejemplo, que se llegaba al equilibrio en varias generaciones. Weinberg estudió también el vínculo de la correlación entre parientes para características cuantitativas (como es el caso de la altura, que había sido demostrada en varias ocasiones a principios de este siglo) y la herencia mendeliana que a principios de siglo generó una gran controversia y demostró, como lo haría, en 1918, R. Fisher, que la herencia de caracteres cuantitativos también podía explicarse utilizando el mecanismo propuesto por Gregor Mendel para caracteres discretos. Este descubrimiento hecho por Weinberg entre 1909 y 1910 no fue conocido por Fisher antes de su trabajo de 1918.

LA MUTACIÓN COMO FUERZA EVOLUTIVA

Las teorías acerca de cuáles aspectos que moldean la dinámica de las poblaciones son más importantes pasaron por varias fases a principios de siglo. Darwin proponía que la selección natural era la fuerza más importante, pero cuando se redescubrieron las leyes de Mendel en 1900 se pensó que la mutación era la fuerza más importante en la dinámica de los genes. Hugo de Vries fue uno de los investigadores que más defendió esta posición. Veamos en que tuvo razón y en qué se equivocó.

La mutación es la fuente de toda variación genética. En una población en la que cada individuo fuera un mutante para el mismo carácter y el gene mutante fuera recesivo, en cada generación se modificaría ese carácter para toda la población. Si por otro lado, sólo un individuo de cada 10 000 000 000 presenta cierta mutación para una población como la humana, en promedio, un individuo de cada dos generaciones presentaría la mutación si el gene mutante fuera dominante. Para saber qué tan importante es la mutación se requiere conocer las tasas de mutación. Si éstas son muy altas, es decir, si la proporción de genes que mutan en cada generación es muy elevada, entonces la mutación es una fuerza muy importante. Si las tasas son muy bajas, lo más probable es que la mutación no sea muy importante para la evolución de las poblaciones.

Las primeras estimaciones de tasas de mutación las realizaron los investigadores Max Delbrñck y Salvador Luria en bacterias. Su sistema de ensayo consistía en hacer crecer números grandes de bacterias (por ejemplo E. coli; uno de los microorganismos que nos ayuda a digerir los alimentos en el intestino) en dos condiciones. La primera era en un gran cultivo de 10 ml y la segunda en 20 frascos de 0.2 ml. En el caso de los 20 frascos se dejaron crecer alrededor de 20 generaciones hasta tener una concentración de 10⁹ células/ml. Después de esto se pusieron las bacterias de los diferentes frascos en cajas de Petri (Figura 28) en presencia de bacteriófagos T1, que atacan las células de E. coli pero para los que algunas cepas de bacterias son resistentes. Del cultivo de 10 ml también se tomaron muestras para poner en cajas de Petri en presencia de bacteriófagos T1. Los resultados que se encontraron se muestran en la Figura 29. Las diez submuestras de la muestra de 10 ml tuvieron cepas resistentes (un promedio de 16.7). De los 20 tubos en donde crecieron en forma independiente se encontraron 11 sin cepas resistentes y 9 con cepas resistentes, un promedio de 11.4. Estos datos demuestran dos puntos. Primero, que la resistencia aparece en forma espontánea, sin que el medio tenga que ver en ello. Segundo, que si la mutación es un fenómeno aleatorio existe una distribución matemática que describe ese fenómeno y por lo tanto se pueden hacer estimaciones de las tasas de mutación. De hecho, para el experimento de Luria y Delbrñck se pudo estimar una tasa de mutación de 3 x 10^-9. Es decir, aproximadamente aparecen tres bacterias resistentes al bacteriófago T1 de cada 1 000 millones de bacterias en cada generación.

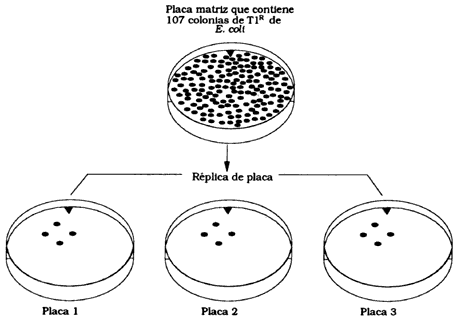
Figura 28. Series de placas de replicación que contiene una elevada concentración de fagos t1 y cuatro colonias T1^r. Un cultivo de 107 células de E. Coli se dispersa en una placa nutritiva y se incuba por corto tiempo para que crezcan colonias pequeñas. La placa, que nunca se ha expuesto al fago T1, es pasada por réplica a tres placas inoculadas con el fago T1. Las colonias T1^r que aparecen en las placas figuran en posición idéntica, lo que indica que deben tener origen común en las colonias T1^r preexistentes en la placa original.

Desde luego, estas estimaciones son relativamente fáciles de hacer en bacterias y virus donde se pueden tener grandes poblaciones para estimar tasas tan bajas. En otros organismos, como por ejemplo en moscas o en plantas de maíz, se tienen que utilizar otros enfoques ya que además, como son especies diploides, la existencia de mutaciones recesivas es oscurecida por los alelos dominantes. Aun cuando existen estas limitaciones, se han podido estimar tasas de mutación en varias especies y para varios genes diferentes, algunos que tienen que ver con fenotipos característicos como el color, para enfermedades como la hemofilia, para capacidades metabólicas como la utilización de ciertas sustancias como la adenina o la presencia de diferentes variantes electroforéticas. Las estimaciones que muestran en la figura 30 indican que los valores de mutación más altos son de alrededor de 10^-4 hasta valores tan bajos como la resistencia a la estreptomicina (4x10^-10). Como ya hemos dicho, estas tasas se refieren a la proporción de células en las que aparece una mutación en una generación. Entonces, por un lado existe una muy alta variabilidad en las tasas de mutación (de hasta un millón de veces de diferencia), mientras que por el otro es claro que las tasas de mutación tienen valores bajos.

Prueba de la fluctuación del origen espontáneo de los mutantes de E. coli resistentes al fago T1
Cultivos individuales			Muestras del cultivo masivo
Número del cultivo	Bacterias T1R encontradas		Número de la muestra	Bacterias T1R encontradas
1	1		1	14
2	0		2	15
3	3		3	13
4	0		4	21
5	0		5	15
6	5		6	14
7	0		7	26
8	5		8	16
9	0		9	20
10	6		10	13
11	107	.	.
12	0		.
13	0	.	.
14	0	.	.
15	1	.	.
16	0	.	.
17	0	.	.
18	64	.	.
19	0	.	.
20	35	.	.
Media (ñ)	11,4	.		16,7
Varianza	694	.		15
Varianza (ñ)	61	.		0.9

Figura 29.

Tasas de mutación de genes específicos de varios organismos.
Organismo y rasgo	Mutaciones por genoma y por generación
Bacteriófago T2 (virus) "Amplitud de huéspedes" Inhibición de la lisis	3 x 10 -9 1 x 10 -8
Escherichia coli (bacteria) Resistencia de estreptomicina Dependencia de la estreptomicina Resistencia al fago T1 Fermentación de la lactosa	4 x 10 -10 1 x 10 -9 3 x 10 -9 2 x 10 -7
Salmonella typhimurium (bacteria) Independencia de triptófago	5 x 10 -8
Chlamydomonas reinhardi (alga) Resistencia de estreptomicina	1 x 10 -6
Neurospora crassa (hongo) Independencia de la adenina Independencia del inositol	4 x 10 -8 8x 10 -8
Zea maiz Semillas arrugadas Semillas purpúreas	1 x 10 -6 1 x 10 -5
Drosophila melanogaster (mosca de la fruta) Variantes electroforéticas Ojos blancos Cuerpo amarillo	4 x 10 -6 4 x 10 -5 1 x 10 -4
Mus Musculus (ratón) Piel marrón Piel manchada	8 x 10 -6 3 x 10 -5
Homo Sapiens (Hombre) Corea de Huntington Aniridia (ausencia de iris) Retinoblastoma (tumor en la retina) Hemofilia A Acondropasia (Enanismo) Neurofibromatosis (tumor del tejido nervioso)	1 x 10 -6 5 x 10 -6 1 x 10 -5 3 x 10 5 4-8 x 10 -5 2 x 10 -4

Figura 30.

¿Cual es la importancia de estas bajas en la evolución de una población? Esta pregunta tendremos que responderla un poco más adelante, cuando sepamos cuáles son los valores de otros valores relacionados con las frecuencias génicas.

LA MIGRACIÓN COMO FUERZA EVOLUTIVA

Uno de los valores que tienen que ver con la dinámica de las frecuencias alélicas en una población es la tasa de migración, es decir, la proporción de individuos de una población que son inmigrantes. La evolución trata de la divergencia entre las poblaciones, de la diferenciación y el aislamiento de poblaciones hasta generar nuevas especies. ¿Qué importancia puede tener, entonces la migración entre poblaciones? Sin lugar a dudas, si es muy grande puede eliminar, la diferenciación genética generada por el aislamiento, puede uniformizar poblaciones que de otra manera divergirían, puede, en resumen, eliminar o en el mejor de los casos retrasar la evolución. Al igual que en las tasas de mutación, la tasa de migración también es una proporción. Es la proporción de individuos de una población que provienen de otra población con diferentes frecuencias génicas. Supongamos, por ejemplo, que ingresan a una población la mitad de individuos de otra población donde la frecuencia de cierto alelo es 1.0, es decir, todos los individuos de esa población tienen un alelo. Si la población de residentes no tiene ese alelo. Así la frecuencia es de cero, es fácil imaginarse que la frecuencia en la población mezclada será de 0.5. La frecuencia de la población mezclada la podemos escribir como una función de la proporción de inmigrantes, m, la proporción de residentes 1-m y las frecuencias en cada una de las poblaciones 1 y 0. Como en el ejemplo m vale 0.5, la frecuencia en la población mezclada será m×1.0 + (1-m) 0.0 = 0.5. Desde luego que la función m es central para conocer la importancia de la migración y difícilmente en una población esta tasa será de 0.5. Normalmente las tasas de migración son menores a, digamos, el 5% de la población residente, de tal manera que se requieren varias generaciones para que la frecuencia génica de los inmigrantes diluya a la de los residentes. En esta situación estamos suponiendo que no existe selección natural, es decir, que no hay alelos que tengan cierta ventaja sobre los demás. También estamos suponiendo que la población que estudiamos es de tamaño infinito, de tal manera que no hay fluctuación y fijación aleatoria de los diferentes genes.

LA SELECCIÓN NATURAL COMO FUERZA EVOLUTIVA

Sin duda, la selección natural es la fuerza evolutiva más conocida para todos nosotros. Es en esta fuerza que Charles Darwin basó su teoría de la evolución. Es ésta la fuerza que hace el que algunos individuos se reproduzcan más que otros y que de esta manera algunos genes aumenten en frecuencia, comparados con otros. Esta fuerza es muy poderosa: En unas pocas generaciones podría llegar a incrementar la frecuencia de estos genes más adaptados hasta fijarlos en algunos casos. En este caso también es la magnitud de un aspecto el que nos dirá si la selección natural puede ser una fuerza importante. Este parámetro es el coeficiente de selección. Es la importancia relativa que un genotipo tiene sobre otro. Por ejemplo, si estamos hablando de sobrevivencia, y uno de los genotipos tiene una probabilidad de sobrevivencia de 0.5, mientras que otros tienen una probabilidad de sobrevivencia de 1.0, es decir, todos los individuos sobreviven, ¿cuántas generaciones pasarán hasta que la población llegue a un equilibrio en las frecuencias génicas?, por ejemplo, si empezamos con frecuencias de 0.50 para el genotipo A₁A₂, 0.25 del genotipo A₁A₁ y 0.25 para el genotipo A₂ A₂. Este último genotipo tiene una sobrevivencia de 0.5 y los otros dos tienen una sobrevivencia de 1.0. En la primera generación, las frecuencias de los adultos de los tres genotipos serán 0.5, 0.25 y 0.125, que al cruzarse (Figura 31) producirán unas frecuencias de 0.51, 0.31 y 0.18, que al ser comparadas con las frecuencias de los adultos en la generación anterior indicarán que la proporción de A₂ A₂ disminuye y la del otro homocigoto aumenta proporcionalmente. De hecho, se puede demostrar que en cada generación la disminución del alelo A₂ se lleva a cabo a una tasa de (P/(P₂ + 2pq + 0.5qñ))-p y que al cabo de aproximadamente 50 generaciones esta frecuencia será menor de 0.01.

Eficacia biológica relativa de polillas Biston betularia claras y obscuras en Dorset, Inglaterra.

	Obscuras	Claras
GENOTIPO	DD y Dd	dd
(a) NÚMERO LIBERADO	406	393
(b) NÚMERO RECAPTURADO	19	54
TASA DE SUPERVIVENCIA (b/a)	0.047	0.137
EFICIENCIA BIOLÓGICA RELATIVA (w)	0.047/0.137=0.043	0.137/0.137=1

Figura 31.

LOS TIPOS DE SELECCIÓN

Si consideramos que la selección es el mecanismo mediante el cual algunos genotipos tienen ventaja sobre otros y analizamos un sistema con tres genotipos y dos alelos como el presentado en la sección anterior, podría haber tres situaciones. La primera es la que presentamos en la sección anterior en la que alguno de los homocigotos tiene una mayor adecuación (en este caso la sobrevivencia) que aquella de los demás genotipos. En la segunda, la adecuación del heterocigoto es mayor que la de cualquiera de los homocigotos. La tercera es aquella en la que el heterocigoto tiene una adecuación menor que la de cualquiera de los homocigotos. Ya vimos que cuando uno de los homocigotos tiene mayor adecuación que los otros dos genotipos, con el paso de las generaciones el genotipo seleccionado será el único que exista y los otros dos desaparecerán. En los otros dos casos los resultados no son tan claros. Cuando la mayor sobrevivencia o adecuación sea la del heterocigoto, la frecuencia al inicio es un factor determinante de lo que le pase a la población. Si esta población no es polimórfica, es decir, que tenga el mismo tipo de alelo, el resultado es trivial porque la población no tiene variabilidad genética para responder a la selección.. Si, en cambio, existe variabilidad genética, entonces el resultado depende de las adecuaciones relativas de los dos homocigotos (Figura 32). Por ejemplo, si las adecuaciones relativas son iguales, la población tenderá a un estado de equilibrio con idénticas frecuencias alélicas. Por el otro lado, si las adecuaciones relativas son diferentes, por ejemplo siendo la adecuación del genotipo A₁A₁ es mayor que la del genotipo A₂ A₂ entonces tendremos un equilibrio en el que la frecuencia del alelo A₁ será mayor que la del alelo A₂. En general, la frecuencia de A₁ en el equilibrio será una función de las adecuaciones de los homócigos en la forma p= (t/s+t) donde s es 1 menos la adecuación del genotipo A₁A₁, y t es 1 menos la adecuación del otro homocigoto. El equilibrio se alcanzará en pocas decenas de generaciones.

En el tercer caso, cuando la menor sobrevivencia o adecuación es la del heterocigoto, también tendríamos equilibrios triviales cuando la frecuencia inicial de cualquiera de los alelos fuera 1. Si por el otro lado, la frecuencia inicial de los alelos es diferente de 1 y de 0 existirá también un equilibrio que será el mismo que en el caso donde la mayor adecuación es la del heterocigoto pero el equilibrio será inestable. Esto significa que si la frecuencia alélica es menor a la del equilibrio, la población se fijará para un alelo, mientras que si la frecuencia inicial es mayor que aquella en el equilibrio, la población se fijará para el otro alelo (Figura 32).

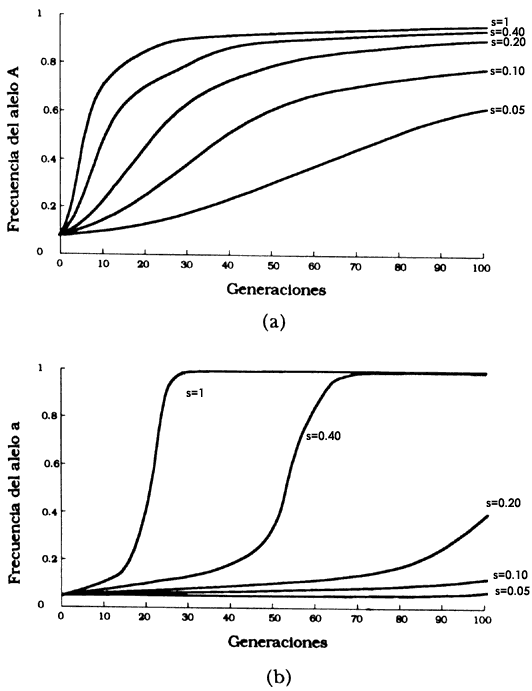
Figura 32(a). Selección direccional que favorece una nueva mutación recesiva. Las curvas muestran la frecuencia del alelo A cuando es introducido con una frecuencia incial de 0.05. Una mutación dominante favorable aumenta considerablemente en frecuencia, aunque la selección sea débil. (b). Selección direccional favoreciendo mutaciones recesivas nuevas. Las curvas muestran la frecuencia del alelo a cuando es introducido con frecuencia inicial de 0.05. Una mutación recesiva con sólo una pequeña ventaja requiere más tiempo para incrementar su frecuencia. Ya que se vuelve común su fijación es rápida

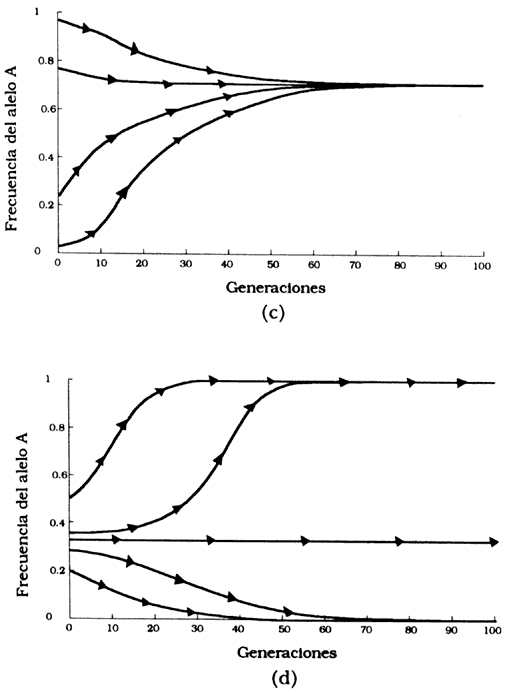
Figura 32(c). Selección cuando hay sobredominancia. Las frecuencias alélicas convergen en el equilibrio sin importar su frecuencia inicial. (d). Selección cuando hay inferioridad del heterocigoto. La frecuencia alélica inicial va 0 a 1 dependiendo de la frecuencia inicial.

Existe una condición más que es interesante mencionar y es que la frecuencia alélica inicial sea idéntica a la frecuencia alélica en el equilibrio. En esa situación la población se mantendrá en el punto de equilibrio, pero tan pronto como la frecuencia alélica se separe sólo un poco de la frecuencia en equilibrio, la población se moverá hacia un equilibrio donde alguno de los alelos tenga una frecuencia igual a uno. El movimiento hacia ese equilibrio también tomará unas pocas decenas de generaciones. (Figura 32).

LA DERIVA GÉNICA COMO FUERZA EVOLUTIVA

Hasta ahora hemos considerado las fuerzas que tienen que ver con ecuaciones que predicen la frecuencia alélica de una población en una generación en función de la frecuencia en la generación anterior. Es decir, hemos trabajado con modelos deterministas. Existe una fuerza evolutiva que en ese sentido es impredecible. Si sólo conocemos la frecuencia de un alelo en una generación y el tamaño de la población N no podemos predecir la frecuencia alélica en la generación siguiente. Podemos predecir, eso sí, la probabilidad de tener cierta frecuencia alélica y también algunos otros valores pero no la frecuencia alélica.

La deriva génica ocurre en el momento de la fecundación de los gametos. De una multitud de gametos, digamos una cantidad infinita, aquellos que llegan a fertilizar o ser fertilizados son finitos. Si el tamaño de esa población de gametos es N, entonces la población perderá heterocigotos a una velocidad que es proporcional al tamaño de la población. En el proceso de la deriva génica no se pierde variabilidad genética, sino que la variabilidad existente se reacomoda entre homocigotos y heterocigotos, aumentando la proporción de homocigotos relativamente a lo esperado con un tamaño infinito de la población.

Una forma de comprender el efecto que tiene la deriva génica es considerar a una población compuesta de una serie de subpoblaciones, con N individuos cada una (Figura 33). Así, por ejemplo si empezamos con 50 subpoblaciones, con un tamaño de seis individuos cada una, en una población con dos alelos con frecuencias de 0.5 cada uno de ellos, con el tiempo, aproximadamente la mitad de las subpoblaciones terminará con solo homocigotos para un alelo y a su vez, la otra mitad de las poblaciones con solo homocigotos para el otro alelo. Si en cambio, las frecuencias iniciales de los dos alelos son 0.9 y 0.1, entonces, aproximadamente el 90% de las subpoblaciones tendrán sólo homocigotos del alelo más común, al paso de varias decenas de generaciones, y 10% de las subpoblaciones tendrán sólo homocigotos para el alelo menos frecuente. El efecto de la deriva génica será entonces en la proporción de homocigosis y variación genética en una subpoblación, pero sólo en la proporción de homocigotos y no en las frecuencias alélicas de la población total. Esto quiere decir que existirá una subestructura de la población original en la que la proporción de homocigotos se modificará. Las subpoblaciones divergirán, se harán diferentes porque en cada una de ellas se fijaran diferentes alelos, al azar pero en función de las frecuencias alélicas originales.

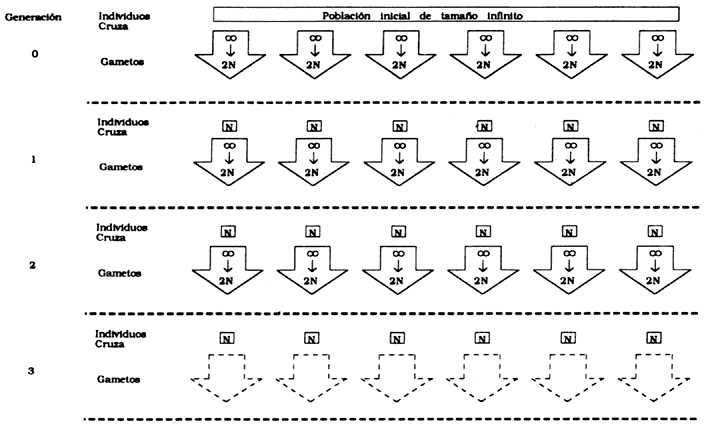
Figura 33(a). Modelo para analizar los efectos de la deriva genética. Cada subpoblación (columnas verticales de cajas y flechas) está genéticamente aislada de otras subpoblaciones. Cada una de ellas produce un número infinito de gametos, de los cuales 2N se escogen al azar para formar la siguiente generación. La deriva genética resulta de errores de muestreo en el proceso.

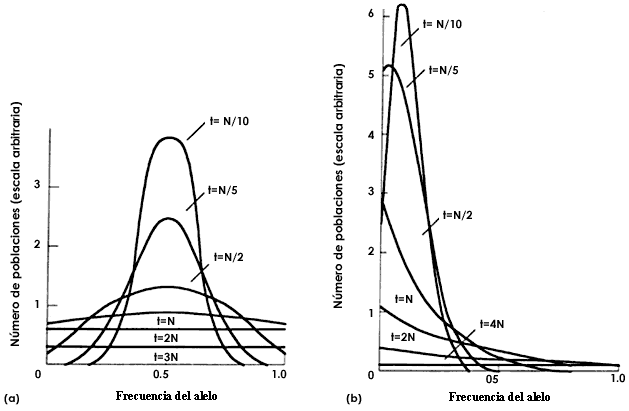
Figura 33(b). Resultados teóricos de la deriva genética. Izquierda (a) frecuencia alélica inicial igual 0.5, (b) la frecuencia alélica inicial es igual a 0.1. Las curvas muestran la distribución de las frecuencias alélicas entre poblaciones que se segregan.

Otra manera de hacerse una idea de la deriva genética es considerando el extremo en que el tamaño de la población es de dos individuos y analizando la forma como evolucionan los diferentes genes. Lo que pasaría con un modelo aleatorio de fijación es que para todos los genes los individuos serían homocigotos, los alelos se fijarían al azar, sólo como una función de su abundancia, de manera que si las frecuencias alélicas son 0.5 y trabajamos con 20 genes, en cada gene se fijará un alelo con una probabilidad de 0.5.

La deriva génica tendrá un efecto sobre la varianza de las subpoblaciones; es decir, esa varianza se hará cada vez mayor porque en cada subpoblación se estarán fijando diferentes alelos en homocigotos (Figura 33), pero no tendrá un efecto sobre la variabilidad genética de las subpoblaciones. La deriva génica disminuye la variabilidad genética dentro de una subpoblación, pero no afecta la variabilidad genética de la población entera.

EL SISTEMA DE CRUZAMIENTO COMO FUERZA EVOLUTIVA

Existen muchas maneras como los organismos se reproducen. Comúnmente, lo que conocemos mejor es el caso en el que a través de la meiosis, los individuos producen gametos que posteriormente se fertilizan. Como ya hemos visto, la meiosis sirve precisamente para que a una hora de la fertilización no se duplique el material genético y se mantenga la cantidad de ácido desoxirribonucleico en los individuos. En algunas especies este proceso no existe, por lo que al no haber fertilización, la meiosis no es necesaria y por lo tanto no se da la mezcla de dos diferentes genomas. Esta reproducción es llamada vegetativa en plantas y partenogénesis en animales. Los padres producen individuos idénticos a ellos. Este fenómeno tiene consecuencias evolutivas muy interesantes porque no permite la recombinación y por ejemplo la selección se lleva a cabo en la misma manera en la que ocurre en especies haploides (con una sola copia de cada gene). En ambos casos, el sistema de cruzamiento no afecta la evolución de la población, pero si por otro lado si la población tiene reproducción sexual entonces dependiendo del tipo de apareamientos, las consecuencias serán diferentes. Por ejemplo, si en plantas en las que existen dos sexos en una misma flor quisiéramos averiguar el efecto que tiene el que la planta se reproduzca a través de semillas provenientes de fertilización con otros individuos versus aquellos en donde la reproducción se lleva a cabo con polen del mismo individuo. Supongamos que partimos de frecuencias genotípicas de A₁A₁, A₁A₂ y A₂A₂ de 0.25, 0.5 y 0.25 con frecuencias alélicas de 0.5 y hacemos que el 100% de los individuos se crucen solamente consigo mismos, en la primera generación tendremos frecuencias de los tres genotipos que serán 0.375, 0.25 y 0.375 y en la siguiente generación tendremos frecuencias genotípicas de 0.4375, 0.125 y 0.4375. En cuatro generaciones más, la frecuencia de los heterocigotos será de 0.0078 y la de los homocigotos de 0.4961 cada uno. Es decir, la frecuencia de los heterocigotos habrá disminuido a una frecuencia menor de 1%. De hecho, en el equilibrio las frecuencias genotípicas de los tres genotipos serán pñF, 2pq (1-F) y qñF donde F es la probabilidad de que los dos alelos de un individuo sean idénticos. Estas frecuencias se dice que están en el equilibrio de Wright para diferenciarlas del equilibrio de Hardy-Weinberg. Cuando la autofecundación es total, es decir, todas las fecundaciones se llevan a cabo por gametos del mismo individuo en el equilibrio, las frecuencias de los homocigotos serán de 0.5 y la de los heterocigotos serán de cero y la población estará alejada del equilibrio de Hardy-Weinberg. A medida que la autofecundación es menos estricta (hay cruzas entre hermanos, primos, primos segundos, etc.), el valor que tome F será cada vez menor y la proporción de los heterocigotos en el equilibrio será cada vez mayor que cero hasta que la fertilización se lleve a cabo entre gametos diferentes, cuando el valor de F será igual a uno.

En las plantas, los sistemas de cruzamiento son mixtos en muchas especies, esto quiere decir que una proporción s de las semillas será producida por autofecundación y otra proporción (1-s o t) provendrá de cruzamientos entre individuos diferentes. En este caso, existe una relación entre la tasa de entrecruzamiento (t) y la probabilidad de tener alelos idénticos en un individuo ( que es F= (1t)/(1+t), de tal manera que cuando todas las semillas de un individuo provienen de cruzamientos entre individuos diferentes, es decir t toma un valor de uno, entonces F tomará un valor de cero y estaremos en equilibrio de Hardy-Weinberg. Si por otro lado, todas las semillas son producto de autofecundación, es decir t vale cero, entonces F en el equilibrio tendrá un valor de uno. Existen formas de estimar la proporción de semillas producto de fertilización entre diferentes individuos para predecir la proporción del exceso de homocigotos en una población.

Entonces, en general podemos decir que el cruzamiento entre parientes ocasiona un exceso de homocigotos en la población y el parámetro F nos ayuda a estimar ese exceso a través de la ecuación del equilibrio de Wright.

UNA SÍNTESIS DE LAS FUERZAS EVOLUTIVAS

Ya hemos visto cómo las diferentes fuerzas evolutivas tienen diversas consecuencias tanto en las frecuencias génicas como en las genotípicas, ahora podemos hacer una síntesis de las diversas consecuencias que tienen estas fuerzas, así como de aquellas que podemos esperar si las combinamos.

Solo una de las fuerzas, la mutación, es fuente de nueva variabilidad genética, aun cuando la migración incrementa la variabilidad genética a nivel local pero no a nivel global. Sólo la selección natural tiene la capacidad de disminuir la variabilidad genética en un nivel global aun cuando la deriva génica la disminuye a nivel local. Cuatro de las cinco fuerzas (migración, selección, deriva génica y sistema de cruzamiento) modifican las frecuencias genotípicas, pero en particular la deriva génica y el sistema de cruzamiento incrementan la proporción de los genotipos homocigotos, alejando a la población del equilibrio de Hardy-Weinberg.

La deriva génica y la selección natural pueden tener el mismo efecto de hacer divergir a las subpoblaciones de una especie y la migración en ese contexto las hará converger, siendo entonces una fuerza opuesta a las anteriores. De las cinco fuerzas evolutivas, cuatro de ellas son deterministas (se pueden predecir las frecuencias alélicas y genotípicas de una generación como una función de la frecuencias en la generación anterior) y una de ellas (la deriva génica) es una fuerza probabilística para la que sólo podemos hacer afirmaciones sobre la probabilidad de que las frecuencias tengan diversos valores.

Los efectos que las fuerzas tienen sobre las frecuencias genotípicas son diversos, pero la deriva génica, el cruzamiento entre parientes y la selección diversificadora incrementan la frecuencia relativa de homocigotos. La selección que beneficia a los heterocigotos y el sistema de apareamiento entre fenotipos diferentes incrementa la frecuencia relativa de los heterocigotos.

LA GENÉTICA DE LOS CARACTERES POLIGÉNICOS

El primo de Charles Darwin, Francis Galton (1822-1911) a finales del siglo XIX gráfico la relación entre la desviación de la altura promedio de los padres contra la desviación de la altura promedio de los hijos y encontró que los hijos de padres más altos que el promedio, eran normalmente más altos que el promedio mientras que hijos de padres relativamente bajos también eran bajos. Este hecho, desde luego, sugiere que debe de existir una relación entre los genes y la altura de las personas. Para entonces, las leyes de Mendel no eran aún conocidas como principios generales y no se tenía una explicación genética para caracteres que, como la altura, no son discretos (como los caracteres que estudió Mendel) sino que se miden. Caracteres discretos son aquellos que tienen diferentes estados. Por ejemplo, los chícharos arrugados y los lisos son sólo dos opciones, la altura, en cambio, si pudiéramos medirla con toda precisión alcanzaría valores, por ejemplo de 1.7945894563729548, por lo que, en principio, el número de estados de caracteres como la altura podría ser infinito. La altura no es un carácter discreto, sino continuo. Lo arrugado o no de los chícharos es un carácter discreto.

Ahora sabemos que la genética de estos caracteres continuos es igual a la genética de los caracteres discretos y que está regida también por las leyes de Mendel. Los caracteres se segregan en forma independiente, y normalmente, para obtener un carácter como la altura se suman los efectos de los alelos en los diferentes genes.

LA SELECCIÓN DE LOS CARACTERES CONTINUOS

¿Cómo operan entonces las fuerzas evolutivas en los caracteres continuos?. Normalmente se comportan como lo hacen en los casos que hemos revisado, pero afectando a los genes que determinan el carácter fenotípico. El efecto de la selección natural sobre los caracteres continuos es interesante en sí mismo ya que es la base de los programas de mejoramiento genético que se han llevado a cabo en animales y plantas para obtener mejores variedades y razas de vacas, trigo, maíz, frijoles, etcétera.

Lo que sabemos es que en los caracteres continuos o como también se les llama, cuantitativos, existe una porción que está determinada por condiciones ambientales. Es decir, parte de la altura que todos tenemos está determinada por la alimentación y las condiciones de crecimiento. Aun cuando tengamos padres altos, si nuestras condiciones ambientales no son adecuadas, no llegaremos a tener la altura que podríamos tener. Existen, entonces, dos causas de nuestra altura, la ambiental y la genética. Podríamos escribir lo siguiente: FE = AM + GE. El fenotipo (FE) es la suma de los efectos del ambiente (AM) y del genotipo (GE). Algunos caracteres como la altura o la producción de leche en las vacas tiene una proporción muy baja del fenotipo determinado por el genotipo. En otros casos, como la forma del cráneo, la proporción del fenotipo que es genética es muy alta. A la proporción del fenotipo determinado por los genes le llamamos heredabilidad. A mayor heredabilidad, mayor será la proporción genética del fenotipo.

MEJORES TRIGOS Y MEJORES VACAS

Este concepto de heredabilidad puede ayudarnos a predecir qué pasaría si quisiéramos seleccionar una característica de una población para cambiarla con el tiempo. Por ejemplo, los frijoles, los maíces y los jitomates que comemos actualmente no son iguales a aquellos frijoles, maíces y jitomates de los que provienen. En el pasado estas especies eran más pequeñas que ahora. Los frijoles silvestres, por ejemplo, tienen la semilla mayor en la actualidad porque el hombre ha sido un agente selectivo constante del tamaño y de otras características, como por ejemplo, el que las vainas no se abran. ¿Cómo se ha llevado a cabo esta selección de características importantes para el hombre? Aun cuando la heredabilidad es un concepto que se describió por primera vez a principios de este siglo, el hombre ha utilizado ese conocimiento desde hace miles de años para obtener especies con características más útiles. Podemos describir este fenómeno con una ecuación R= hñ X S. La respuesta a la selección (R) es una función de la fuerza de la selección (S) y de la heredabilidad (hñ). Si la heredabilidad es uno (esto es, toda la variación fenotípica es producida por variación genética), entonces la respuesta a la selección será igual a la fuerza de la selección. Esto es, si en una generación seleccionamos sólo aquellos frijoles mayores de 1 cm, todos los frijoles que se produzcan de ellos serán también mayores de 1 cm. Si en la siguiente generación seleccionamos sólo aquellos frijoles mayores de 1.1 cm, todos los frijoles producto de aquellos seleccionados tendrán también más de 1.1 cm. Desde luego, en estas características cuantitativas la heredabilidad nunca es 1 por lo que al seleccionar aquellos frijoles mayores de 1 cm, algunos de los frijoles que se produzcan de ellos tendrán más de 1 cm, pero otros seguirán siendo menores que 1 cm. Este proceso llamado selección masal, llevado a cabo por varias generaciones, generará en un tiempo más o menos largo el que tengamos frijoles de mayor tamaño, colores particulares, mayor rendimiento y en algunos casos, más resistentes a plagas y enfermedades. Así es como hemos obtenido mejores plantas para alimentarnos, en particular aquellas que son la base de la alimentación de una altísima proporción de la población de la Tierra, como el trigo, el maíz, el arroz, el frijol y la papa.

En el caso de las vacas y otros animales el procedimiento más común para obtener animales con características apropiadas es a través de la cruza y selección posterior de animales deseables. Es decir, si tenemos dos cerdos, uno con pelaje fuerte y otro con buena calidad de carne, los cruzamos y de los hijos seleccionamos aquellos que tengan ambas características. Haciendo esto por varias generaciones, poco a poco se irán obteniendo animales económicamente más valiosos. A veces esto no es posible porque los alelos que determinan una característica deseable también traen consigo características indeseables, por lo que no es posible tener ambos caracteres en un mismo individuo; es por ello que en muchas especies se mantienen diversas variantes. En el caso de los cerdos se mantienen variantes de pelaje, de grasa, de carne, etc., pues no es posible tener un solo cerdo que posea todas estas características deseables.

En las plantas también se puede introducir caracteres particulares en variedades económicamente importantes llevando a cabo cruzas y haciendo selecciones. Por ejemplo, es posible introducir genes de resistencia a plagas en un proceso que abarca varias generaciones. Estas cruzas se hacen de la siguiente manera. En una primera cruza de las dos variedades se eligen aquellos individuos de la progenie que poseen una combinación de las características deseadas en particular la resistencia a las plagas. En una segunda cruza del híbrido de la primera con la variedad sensible, de la progenie se eligen aquellos que, manteniendo la resistencia, se parezcan más a la variedad sensible. Esta retrocruza continua con uno de los progenitores (aquel que siendo sensible tiene las mejores características útiles) garantiza que, aproximadamente entre seis y 10 generaciones se obtenga una variedad mejorada que manteniendo sus características agronómicas a la vez sea más resistente.

LA INCORPORACION DE GENES DESEABLES POR MEDIO DE TÉCNICAS MOLECULARES

Acabamos de ver una manera tradicional de introducir un gene en una variedad, pero recientemente se han desarrollado otras tecnologías para transferir genes específicos de una especie a otra. En particular, en las plantas se utiliza la capacidad de la bacteria Agrobacterium tumefaciens para atacar específicamente algunas especies de plantas, formando callos, y se sabe que genes de esta bacteria se transfieren a la planta, de tal manera que algunos genes pueden ser introducidos a las bacterias y luego, a través de ellas, a las plantas. Es una versión elegante de la transformación que llevó a muchos investigadores como Griffith en 1927 y posteriormente a Tatum y Beadie en 1941 a iniciar la demostración de que el ADN es el material hereditario (véase el capitulo III). Esta capacidad de transformación lleva a pensar que se puede hacer ingeniería genética en casi cualquier genoma, pero la realidad es que todavía estamos lejos de poder hacerlo en una forma significativa y mucho menos generalizada. No solamente se trata de transferir la información genética, debemos asegurar que una vez transferido, el gene funcione bien y sea regulado correctamente en la especie receptora; también debemos confirmar que el gene transferido no altere la capacidad de la especie de desarrollarse en forma normal en los ecosistemas. Es decir, no solamente debemos conocer la tecnología de transferencia y los mecanismos de regulación de la expresión génica, de las que se encargan la ingeniería genética y la biología molecular, sino que también debemos conocer la ecología de la especie que estamos estudiando. Pongamos por ejemplo al grupo de bacterias fijadoras de nitrógeno y que forman nódulos en las raíces de las plantas leguminosas de la familia de los frijoles. Estas bacterias del género Rhizobium tienen genes que asimilan el nitrógeno atmosférico. Las consecuencias de la manipulación de estos genes, aun dentro de especies del género Rhizobium, es enorme y por más de una década varios grupos de investigación han estado trabajando, por un lado en aspectos de ingeniería genética, viendo las maneras como se puede transformar Rhizobium, y por otro, tratando de entender qué son y cómo funcionan los genes de fijación de nitrógeno. Aun cuando este trabajo se sigue llevando a cabo todavía es incierto el futuro. Por ejemplo, cuando se tengan las cepas mejoradas de Rhizobium, y se liberen en los ecosistemas naturales, ¿qué les pasará una vez liberadas?, ¿podrán competir ecológicamente con las cepas nativas del suelo?, si recombinan muy frecuentemente con otras cepas nativas ¿cada cuánto tiempo habría que introducirlas en el suelo para que no se diluyan y dejen de ser un componente importante? Es importan resolver estas preguntas y es claro que tenemos ante nosotros un largo camino de investigación por recorrer antes de que la humanidad sea capaz de llevar a cabo este tipo de ingeniería genética a niveles de aplicación generalizada en nuestra sociedad. El hombre siempre ha realizado sus sueños más imaginativos y la ingeniería genética es uno más de esos sueños; sí, el camino es difícil, pero con tiempo y esfuerzo podrá cristalizarse en una realidad cotidiana.