VI. UNA CUBETA EN ROTACIÓN

El sistema del mundo sólo oscila alrededor de un estado medio del que nunca se aparta salvo por una cantidad muy pequeña. ...P. S. LAPLACE (1788)

A FIN de poder explicar mejor la causa de que se produzca el efecto de Coriolis en la superficie terrestre, permítaseme empezar por un caso más sencillo: sea una cubeta de agua a la que se obliga a rotar en forma uniforme en dirección antihoraria y, una vez que la forma de su superficie alcanza el equilibrio, se la congela; la idealización que estamos haciendo es que esta superficie no ejerce ninguna fuerza de fricción sobre cuerpos que se mueven sobre ella. Vamos primero a analizar las fuerzas que actúan sobre una partícula que gira con la cubeta y luego haremos otro tanto con un objeto que se mueva respecto de ella. Las descripciones se harán desde dos puntos de vista: el de una observadora fija al laboratorio y el de uno que está fijo a la cubeta: Inercina y Rotancio, a quienes ya conocimos en el capítulo III.

Partículas en la superficie: Sistema inercial

En la figura se representan las fuerzas que actúan sobre un cuerpo que gire con la cubeta, en un punto de la superficie. Desde el punto de vista de Inercina, la resultante del peso del cuerpo P (que es vertical) más la reacción del hielo R_N (que es normal a la superficie, ya que no hay fricción) es una fuerza horizontal proporcional a la distancia al eje de rotación; ésta es la fuerza que produce la aceleración centrípeta a, es decir, que mantiene la rotación. (Nótese que estoy usando flechas sencillas para representar todos los vectores.) De hecho, de esta construcción y la suposición de rotación uniforme se deduce la forma de la superficie, que en este caso es un paraboloide de revolución (es decir, la sección mostrada en la figura es una parábola).

Partículas en la superficie: Sistema no inercial

En esta figura se muestra el equilibrio de fuerzas desde el punto de vista de Rotancio, quien gira con la cubeta y por lo tanto ve al cuerpo en reposo. Según Rotancio hay tres fuerzas que están en perfecto equilibrio (o sea, que su resultante es nula): el peso P la reacción del hielo R_N y la fuerza centrífuga F_CF. En resumen:

Inercina: Peso + Reacción normal = Aceleración centrípeta

Rotancio: Peso + Reacción normal + Fuerza centrífuga = 0

donde la suma se realiza teniendo en cuenta no sólo la magnitud, sino también la dirección y sentido de las fuerzas (es decir, "+" indica el proceso de calcular la resultante). Matemáticamente tan sólo se ha dicho que la aceleración centrípeta = fuerza centrífuga, pero las experiencias de ambos observadores son bien diferentes: uno ve al cuerpo girar y el otro lo ve en reposo; no es difícil percibir la analogía con el caso de la piedra de la honda (segunda figura del capítulo III) que también analizaron nuestros personajes.

Antes de estudiar movimientos más interesantes sobre la superficie congelada, supongamos que existe gente muy chiquita, de manera que lo que vemos como un simple punto girando con ella es toda una ciudad, Cubetópolis, con todo y su Universidad con su correspondiente laboratorio de física.

Definición de "peso" y "vertical" local

Para los cubetícolas, "vertical" y "horizontal" significan perpendicular y tangente a la superficie, respectivamente. Al igual que en la Tierra, estas direcciones dependen del lugar donde se esté; —usó las comillas para no confundirlas con la dirección del eje (de rotación) de la cubeta que es la dirección del peso (tal y como lo mide Inercina, por ejemplo)—. En cambio, para los buenos albañiles cubetícolas, "vertical" es la dirección de la plomada; es más, ellos llaman "peso" a una fuerza igual en magnitud y dirección, pero de sentido contrario, a la reacción del hielo, es decir

Cubetícola: "Peso" + Reacción normal + 0.

Los físicos cubetícolas luego de mucho estudiar (y de viajes a tierras extranjeras, esto es, a otros puntos de la cubeta), descubren que "vertical" y "peso" son conceptos locales, es decir, que constituyen una función de la distancia al centro de la cubeta, al que llaman "polo". Más precisamente, enuncian que "peso" = peso + centrífuga, donde peso, sin comillas, es la atracción gravitatoria de una tortuga gigantesca sobre la que gira la cubeta congelada; la "vertical" es la dirección del "peso". Los terrícolas tenemos por supuesto más en común con los cubetícolas que con Inercina.

En Cubetópolis vive un físico cuyo nombre es Bonifacio Ordóñez, pero que insiste en ser llamado Newtonius Coriolensis (nadie le hace caso). Bonifacio se dedica a estudiar el movimiento de los objetos sobre la superficie de Cubetópolis, la cual, como sabemos, no ejerce ninguna fuerza de fricción. Ha descubierto que siempre que le da impulso a un pequeño objeto, éste se mueve aproximadamente en un círculo, como si existiera una fuerza que lo desviara continuamente hacia la derecha. El tiempo que tarda el cuerpo en recorrer el círculo es el mismo en todos los experimentos (aproximadamente igual a la mitad del periodo de rotación de la cubeta). Por lo tanto, el diámetro de cada círculo es proporcional a la rapidez con que se mueve el cuerpo en cada experimento, la cual permanece constante.

Voy ahora a analizar como explica Inercina el movimiento de los objetos de Bonifacio. Para ella todo cuerpo en la superficie de la cubeta congelada está sujeto a la acción de dos fuerzas reales. Una es la fuerza normal R_N ejercida por la superficie del hielo, la que se halla dirigida en la dirección "vertical" local y no puede influir el movimiento "horizontal". La otra, en cambio, es el peso P que sí tiene una componente horizontal, dirigida hacia el centro de la cubeta P_H Esta fuerza central, la componente "horizontal" de P, es la clave que tiene Inercina para explicar los experimentos de Ordóñez.

El peso real tiene una componente "horizontal"

Inercina aplica la ley de Newton y descubre que los movimientos posibles bajo la acción de esta fuerza central son siempre oscilaciones alrededor del centro de la cubeta. Algo así como las órbitas de los planetas alrededor del Sol, con la diferencia importante que en el último caso, la fuerza aumenta al acercarse al astro rey, mientras que en el caso de la cubeta esta fuerza disminuye al ir hacia el centro. Esta diferencia se refleja en el hecho que el tiempo en que tarda cada planeta en girar alrededor del Sol varía; desde tres meses en el caso de Mercurio a 250 años en el de Plutón, mientras que todos los cuerpos que orbitan en la cubeta tardan lo mismo en dar una vuelta. En particular todas las microciudades que están en la cubeta (una de las cuales es Cubetópolis) lo hacen al unísono; que las distancias entre ellas permanezcan constantes es lo que permite establecer el concepto de un país en la superficie de la cubeta (obviamente, Cubetolandia).

Vistas desde arriba, las trayectorias que calcula Inercina con la información exclusiva de la forma de la superficie, varían en forma desde un círculo a una línea recta, pasando por elipses con todas las excentricidades posibles. (Estoy suponiendo que estas trayectorias se encuentran cerca del centro de la cubeta; luego trataré el caso más general.) En la siguiente figura se muestra dos de esas órbitas. La circular es nada menos que la trayectoria del laboratorio del doctor Ordóñez, mientras que la elíptica es la de uno de los objetos cuyo movimiento estudia Bonifacio, tal y como lo observa Inercina.

El experimento de Ordóñez visto por Inercina

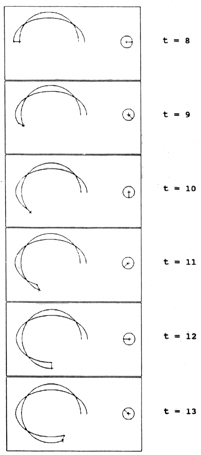
Nuestro interés está puesto en describir los movimientos absolutos de Bonifacio Ordóñez y de su objeto y de ahí, deducir el movimiento relativo de este último, visto por el científico en rotación. En las siguientes figuras se puede apreciar cómo se van desarrollando ambos movimientos, en intervalos de 1/16 del tiempo necesario para dar una vuelta completa. Del lado izquierdo está lo que registra Inercina (movimiento absoluto) y del derecho lo que observa Bonifacio (movimiento relativo).

Inicialmente, t = 0, ambos observadores coinciden en la posición en que está el objeto:

En ambas partes, la flecha va desde Ordóñez al objeto, es decir, indica la posición de este último relativa a la del científico. Un tiempo después, esta es la situación

Nótese que, para Inercina, Ordóñez no sólo está girando, sino que su orientación también varía (como varía también la de nosotros, los terrícolas, a lo largo del día, respecto de las estrellas fijas). La orientación del laboratorio de Ordóñez está indicada por una pequeña cruz (símbolo de los problemas presupuestarios por los que pasan los científicos de Cubetópolis). Del lado derecho, que es el laboratorio de Ordóñez, la cruz está obviamente fija.

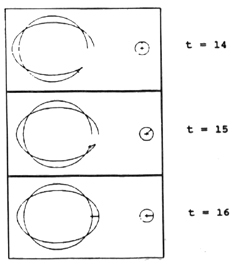
A medida que pasa el tiempo, se observa lo siguiente:

Inercina verifica que el objeto se mueve más despacio que Ordóñez cuando está más alejado del centro que él, y más lento cuando se halla más cerca,¹⁹ es decir, el objeto se retrasa en los puntos lejanos del eje y se adelanta en los cercanos. Don Bonifacio lo percibe como una rotación relativa del objeto, en el sentido opuesto al que gira la cubeta y al doble de velocidad angular. Por ejemplo, para t = 4 tanto Bonifacio como el cuerpo han girado 90ñ en el sentido antihorario respecto del espacio absoluto (lado izquierdo) pero aquél registra que éste ha girado 180ñ y en el sentido horario (lado derecho). Este movimiento relativo es lo que llamamos una oscilación inercial; el factor dos (que aparece por ahí en el texto de G. Coriolis) se debe a que no sólo la posición relativa del objeto cambia, sino que también lo hace la orientación del laboratorio (indicada por la cruz).

La explicación anterior es válida siempre y cuando Cubetópolis se halle cerca del centro de la cubeta, lo que en nuestro caso equivale a estar cerca de un polo, lugar donde el periodo de una oscilación inercial es de medio día. En lo que toca a puntos alejados del centro de la cubeta (o del polo, en el caso de la Tierra), el movimiento es un poco más complicado en el sentido de que el periodo de oscilación inercial es mayor y, desde el punto de vista de Inercina, la órbita del objeto no forma una elipse cerrada. De todos modos, la conservación de momento angular implica que el objeto gira más rápido que Cubetópolis cuando está más cerca del eje y más lento cuando se aleja lo que es percibido por Rotancio como una oscilación en sentido contrario al de la cubeta.

Lo anterior constituye una explicación sencilla de la oscilación inercial desde el punto de vista de Inercina, es decir, sin poner en juego fuerzas ficticias. La clave de la explicación es la componente en el plano "horizontal" local del peso (cuarta figura) debida a la forma de la superficie de la cubeta. La existencia del efecto de Coriolis en la Tierra está también ligada a su forma, más precisamente, a la deformación de su superficie respecto de una esfera perfecta, lo que constituye el tema del capítulo VIII.