I. GALILEO... ma non troppo

Si he podido ver lejos fue porque me paré sobre hombros de gigantes. ........................... .I. NEWTON

 

GALILEO GALILEI (1564-1642) fue un grande entre los gigantes. Se le suele recordar como el fundador del método experimental de la física; su imagen va asociada con la del telescopio y el plano inclinado, con los instrumentos que diseñó y armó para observar y medir. También es famosa su polémica con los aristotélicos de su tiempo que se limitaban a citar a los clásicos y pensar cómo debían ser los movimientos de los cuerpos, en vez de observarlos. Por último, ¿quién no conoce la anécdota del atrevido maestro arrojando dos cuerpos de diferente peso desde la Torre de Pisa? (Anécdota probablemente apócrifa pero, como dicen los italianos, Se non ñ vero... ñ ben trovatto! )

Galileo y el péndulo

Pero, además de señalar la importancia que Galileo dio a la observación, creo que es igualmente justo destacar su capacidad para extrapolar los resultados de los experimentos hacia casos ideales, estrictamente inalcanzables. Galileo fue también un maestro de lo que Ernst Mach llamaría, muchos años después, los Gedankenexperimente, los "experimentos pensados". Voy a referirme enseguida a dos de estas generalizaciones: las que en términos modernos conocemos como el principio de inercia y la ley de composición de velocidades:

En su primera versión del libro de Dialoghi,¹ publicado en 1632, Galileo representa su eterna controversia con los aristotélicos de su época por medio de un diálogo entre Salviati y Simplicio, nombre éste por demás significativo ñno necesito decir quién es quien! Salviati le hace conducir a Simplicio, sin demasiada dificultad, que un móvil en una superficie inclinada hacia abajo se acelera (es decir, aumenta su velocidad), mientras que en una inclinada hacia arriba se frena. Habiendo llegado a esto, le pregunta:²

SALVIATI.- [...] Ahora dime, ¿qué le pasaría al mismo móvil en una superficie sin pendiente hacia arriba o hacia abajo? SIMPLICIO.- [...] Ya que no hay pendiente hacia abajo, no hay tendencia natural al movimiento; y ya que no hay pendiente hacia arriba, no hay resistencia a ser movido, de manera que habrá una indiferencia entre la tendencia y resistencia al movimiento... va a permanecer estable. Como Simplicio no parece darse por aludido, debe insistir: SALVIATI.- [...] Pero, ¿qué pasaría si se le diera un ímpetu en una dirección?... SIMPLICIO.- [...] No veo causa para aceleración o deceleración... SALVIATI.- ¿Cuán lejos se movería la bola? (Acorralado, Simplicio concede.) SIMPLICIO.- ... Tanto como continuara la superficie.

De esta forma, Galileo enuncia entonces el principio de la inercia: En ausencia de fricción (ésta es la gran generalización del maestro) o de otra fuerza que actúe en la dirección horizontal, un cuerpo impulsado sobre una superficie plana se mueve tanto como se extienda ésta.

Algo que es muy interesante para nuestros propósitos es que la imaginación de Galileo no se limita a una superficie plana, a algo pequeño, que pueda caber en un laboratorio. Por lo contrario, enuncia así su idea de una "superficie sin límites";

SALVIATI.- Si la superficie fuera sin límites, el movimiento sería también sin límites... perpetuo. Para que una superficie no esté [inclinada] hacia arriba o hacia abajo, todas sus partes deben estar igualmente distantes del centro. [de la Tierra].

Un barco, cuando se mueve sobre un mar calmo, es uno de esos móviles que va sobre un superficie que no está inclinada hacia arriba o hacia abajo, y si todos los obstáculos externos [fricción con el aire y el agua] y accidentales fueran removidos, seguiría moviéndose en forma incesante y uniforme por el impulso que recibió.

Cuarenta años después de la traumatizante llegada de los europeos a América, Galileo está pensando en una esfera, en el globo terráqueo. Es más, está pensando en el mar y le asigna forma esférica al océano en reposo. Esto es lo que llamamos "nivel del mar" cuando nos referimos a la altura de una montaña o a la en que se mueve un satélite artificial.

Punto clave de esta idealización de Galileo es la ausencia de toda fricción, ni con el agua ni con el aire; para ilustrar mejor esta situación, podemos imaginarnos que la superficie perfectamente lisa del mar en reposo esté congelada (ñquien haya caminado sobre el hielo sabrá muy bien de su escasa fricción!). Según Galileo, un cuerpo que se mueva sobre esta esfera ideal, sin fricción (ni ninguna otra fuerza externa), lo hace sin cambiar ni de rapidez, ni de dirección.

Que no cambie de rapidez, es un concepto fácil de entender: recorre espacios iguales en tiempos iguales. En cuanto a que no cambie su dirección, no significa que la bola se mueva en línea recta, ya que de hacerlo abandonaría la superficie de la Tierra; lo que sí quiere decir es que el móvil se traslada a lo largo de un círculo máximo de la esfera. ¿Y qué es un círculo máximo? Al cortar una rebanada de alguna fruta, el tajo es aproximadamente un círculo; cuanto más esférica sea la fruta y más recto vaya el cuchillo tanto más cierto será esto. Los matemáticos enuncian solemnemente lo anterior diciendo que "la intersección de una esfera con un plano es un círculo". Estos círculos pueden ser tan pequeños como uno quiera (basta cortar, casi rozando, la fruta); pero no pueden ser tan grandes como uno quiera: los mayores se obtienen con cortes (o, la intersección con un plano) que pasen por el centro de la esfera. Este es un círculo máximo.

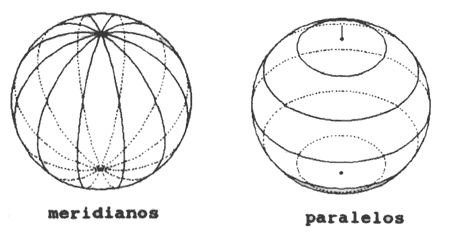
Hay una infinidad de círculos máximos, porque hay una infinidad de planos que pasan por el centro de una esfera. Dos círculos máximos diferentes se cruzan en dos puntos: en la esfera no hay "paralelas" (ya que los círculos máximos son en ella el equivalente de las líneas rectas). Pensando en nuestro planeta, sus meridianos (que unen a ambos polos) son la mitad de un círculo máximo, pero los paralelos no son círculos máximos, salvo el ecuador.

Por lo tanto, de acuerdo con Galileo, si el móvil es impulsado hacia el Norte —o hacia el Sur— en este mar congelado idealizado, seguirá sobre el meridiano en que estaba en un principio (es decir; no cambiará su longitud geográfica), dando una vuelta a la Tierra en el tiempo que le lleve recorrer los 40 000 000 de metros de la circunferencia terrestre. Algo similar ocurriría si se le impulsara hacia el Este —o hacia el Oeste— desde algún punto en el ecuador: esta vez seguiría en el ecuador; no cambiaría su latitud geográfica

Pero los otros paralelos terrestres no son círculos máximos (de hecho, tienen un perímetro menor que el del ecuador) y, por lo tanto, el movimiento inercial de Galileo no puede darse a una latitud fija diferente de cero, o sea, sobre un paralelo. Si, por ejemplo, se diera a la bola un impulso hacia el Este desde una latitud de 60ñN y una longitud 0ñ (punto inicial en la figura siguiente), se vería —de acuerdo con Galileo— que iría acercando al ecuador, cruzándolo a los 90ñE, alcanzando luego las antípodas del punto inicial (60ñS & 180ñE en la parte oculta de la trayectoria), para volver a cruzar el ecuador en los 90ñO y finalmente llegar al punto inicial. En todo ese tiempo, el móvil se habrá estado moviendo —además de sobre la esfera— a lo largo de un plano que tiene una inclinación de 60ñ en relación con el plano ecuatorial. Para hacer la figura, se le otorgó una velocidad de 1 389 km/h, lo que implica que le toma al cuerpo 28.8 h dar una vuelta completa; cada flecha corresponde a una hora de recorrido (la última está a las 28 h de su salida).

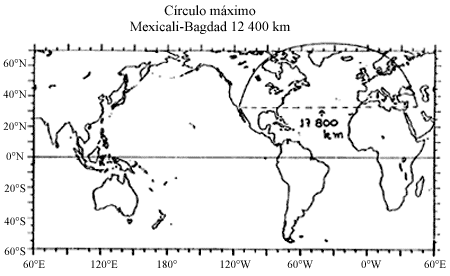
Es importante darse cuenta de que el recorrido sobre la esfera tiene la misma extensión que de aquella sobre el ecuador o a lo largo de los dos meridianos en los ejemplos anteriores. Los geómetras demuestran que el recorrido más corto entre dos puntos y sobre la superficie de una esfera es sobre un círculo máximo. Es por eso que a veces las rutas de los aviones se ven raras sobre un mapa (plano) pero no lo son sobre el globo. Por ejemplo, para ir por el camino más corto desde Mexicali (en Baja California) a Bagdad (en Irak), ambos a aproximadamente 33ñN, hay que desplazarse bastante hacia el norte: el punto medio de la trayectoria se encuentra a los 75ñN y 37ñO. La distancia mínima entre estas dos ciudades es de 12 400 km; mientras que la ruta entre ambas ciudades a lo largo del paralelo 33ñN (que parece recta en un mapa) tiene de longitud 17 800 km. (Quien tenga un globo terráqueo puede verificarlo tensando un hilo entre los dos puntos, o entre otro par; para encontrar la ruta más corta entre ellos.) En el diskette que acompaña este libro pueden encontrar el programa Planeta, con el que pueden experimentar sobre distancias y círculos máximos en la esfera.

Círculo máximo. Mexicali-Bagdad 12 400 km

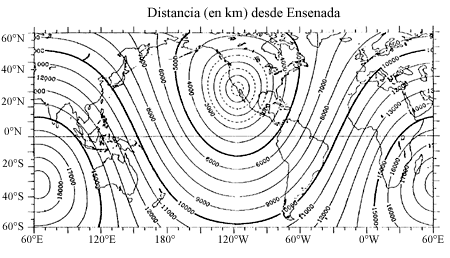
Distancia (en Kilometros) desde Ensenada. Nótese la deformación de estos círculos al proyectarlos sobre un mapa plano.

Posteriormente, Galileo formuló el otro concepto que quiero mencionar aquí: el que actualmente conocemos como la ley de adición de velocidades. Para esto, pone en manos de Salviati la tarea de hacer deducir a Simplicio el lugar donde aterriza una piedra dejada caer desde la punta del mástil de un barco en movimiento uniforme (nuevamente despreciando toda fricción con el aire). Simplicio, por supuesto, está convencido de que la piedra debe caer hacia atrás, hacia la popa; sin embargo su amigo le hace ver que...

SALVIATI.- Aquella piedra en la punta del mástil se mueve también en una circunferencia [...] tan rápido como el barco. SIMPLICIO.- [Entonces] la piedra no va a abandonar el barco, [...] sino que va a caer en el mismo lugar que lo hizo cuando la nave estaba quieta.

Galileo imagina al barco y a la piedra realizando el mismo movimiento horizontal, es decir; en una circunferencia alrededor del centro de la Tierra. La piedra tiene además un movimiento vertical, de caída hacia el centro de nuestro planeta, que se combina con el anterior de manera que llegue exactamente a la base del mástil. Es interesante ver cómo Galileo razonaba de acuerdo con una geometría esférica, fue posteriormente que se cambió sus superficies horizontales de esféricas a planos; aquí respetaremos la imagen original del maestro.

Habiendo recordado estos dos grandes resultados de Galileo (el principio de la inercia y la ley de adición de velocidades) voy ahora a hacerles una corrección debida a la rotación de la Tierra: en primer lugar; la bola que es impulsada sobre el mar sin fricción, no se mueve "sin cambiar su dirección" (es decir, a lo largo de un círculo máximo), sino que es desviada hacia la derecha si está en el hemisferio septentrional o hacia la izquierda en el hemisferio austral. En segundo lugar, la piedra que es dejada caer desde la punta del mástil, sin ningún impulso horizontal, no aterriza exactamente en la base de aquél, sino lo hace un poco hacia el Este. Estas dos correcciones corresponden a lo que ahora se denomina el efecto de Coriolis.

El párrafo anterior no debe ser tomado como una crítica al gran maestro: ambas correcciones son ridículamente pequeñas para el caso de los experimentos que realizó Galileo, por lo que es imposible que él las hubiera detectado, mucho menos predicho ñtodavía no existía la mecánica! De hecho, no fue sino hasta 1851 —219 años más tarde— que el físico francés Juan Bernardo León Foucault (1819-1868) demostró la realidad de la rotación terrestre mediante el péndulo que ahora lleva su nombre.

El péndulo que construyó Foucault tenía unos 60 metros de largo y fue colgado, en el Panteón de París, de un soporte bien diseñado de modo que no ejerciera fuerzas laterales. Foucault utilizó un cordel auxiliar para sujetar la masa del péndulo en posición inclinada respecto de la vertical. Luego de esperar el tiempo suficiente para que todo el sistema estuviera en reposo, Foucault quemó el cordel con el objeto de que el péndulo empezara a oscilar sin darle ningún impulso lateral; la dirección de oscilación era fácilmente observable porque la punta del aparato marcaba su trazo sobre arena fina en el piso.

Uno esperaría que bajo estas circunstancias el péndulo, tan cuidadosamente preparado, siguiera siempre oscilando en el mismo plano vertical. No fue así: se observó que este plano giraba muy lentamente, 11.3ñ por hora, en la dirección horaria (la de las manecillas del reloj).³ Al cabo de unas ocho horas estaba oscilando en un plano perpendicular al inicial. Para comparar ambos movimientos, nótese que el periodo de ese péndulo es de tan sólo unos 16 segundos; al llegar a un plano de oscilación perpendicular al original, el péndulo había realizado ya unas mil ochocientas oscilaciones: El efecto de Coriolis es muy pequeño, pero se va acumulando poco a poco con el tiempo.

Este experimento causó gran sensación, tanto en los medios científicos como entre el público en general, logrando que se terminara por aceptar la realidad de la rotación terrestre. Todavía en la actualidad nos maravillamos con este fenómeno, ya que hay péndulos de este tipo en muchos museos científicos. En vez de mostrar su precesión con un trazo en arena, lo hacen generalmente volteando unos postecitos colocados en el piso formando un círculo de radio inferior a la máxima desviación del péndulo. El efecto se manifiesta tan lentamente que uno normalmente no tiene la paciencia de esperar a que caiga el siguiente postecito: le cree a los encargados del museo cuál era la dirección de oscilación del péndulo a la hora en que se abrió el edificio.

Lo anterior no quiere decir que el efecto de Coriolis sea tan sólo una curiosidad, sin importancia práctica. Como veremos más adelante, este fenómeno es en realidad fundamental para la física de los océanos y las atmósferas planetarias. Es, en consecuencia, importante explicarlo, decir por qué, en ausencia de fuerzas horizontales —de fricción u otras— un cuerpo tiende a desviarse de la dirección en que es impulsado, hacia la derecha en el hemisferio septentrional, o hacia la izquierda en el austral. Hay tres preguntas interesantes que contestar: ¿cómo es que esta desviación de la horizontal se relaciona con la rotación terrestre? ¿Por qué un cuerpo que se deja caer en forma vertical se desvía hacia el Este? y ¿por qué gira el plano de oscilación del péndulo de Foucault? A responder estas preguntas —y a otras cosas más— está dedicado este libro.