II. ¿EXPLICACIONES?
| Muchos están satisfechos [...] de aceptar la idea de una fuerza de
Coriolis, más o menos con una fe ciega, confiados de que ha sido derivada
con rigor.
.......................................
|
UNO de los fenómenos más populares debidos al efecto de Coriolis tiene que ver con el sentido en que gira el agua al vaciarse un fregadero, o de cualquier recipiente al que se le hace un agujero en el fondo: en el hemisferio norte lo hace en el sentido de las agujas del reloj, o sentido horario, y en el hemisferio austral lo hace en el opuesto, el antihorario. (¿Hacia qué lado gira en la ciudad de Quito?) Este es un ejemplo de la tendencia de desviarse hacia la derecha o la izquierda, en cada uno de los hemisferios, que es la primera de las tres preguntas que prometimos responder en el capítulo anterior. Este fenómeno tan conocido ayuda a la popularidad del efecto de Coriolis, pero no a entender sus causas. Concretamente, nos preguntamos:
1) ¿Por qué los cuerpos que se deslizan sobre una superficie horizontal —sin fricción— se desvían de su curso?
2) ¿Por qué al soltar un cuerpo sin darle ningún impulso en la dirección horizontal, cae hacia el Este de la dirección vertical? y
3) ¿Por qué cambia el plano de oscilación del péndulo de Foucault?
Es posible que no todos los lectores estén familiarizados con estos tres fenómenos, pero son bastante comunes, al menos en el sentido de estar descritos en la mayoría de las enciclopedias y muchos libros de divulgación (además de los libros de ciencia, claro está). Las siguientes tres explicaciones respectivas son también muy comunes:
1) Desviación en la horizontal. Este fenómeno es debido a que no todos
los puntos de la Tierra se mueven con la misma velocidad: la Tierra gira alrededor
de su eje dando una vuelta completa aproximadamente cada 24 horas. Como su perímetro
es de unos 40 000 000 m, cualquier punto del ecuador (fijo al globo) se mueve
con una velocidad de 1 670 km/h). Otros puntos fijos a la Tierra se mueven más
despacio, tanto más despacio cuanto más cerca estén de un polo, ya que su distancia
al eje de rotación terrestre es menor.4![[Nota 4]](../img/mcommnt.gif)
La velocidad (tangencial) de un punto sobre la tierra depende de la latitud
Por ejemplo, en las latitudes de 30°N y 45°N esta velocidad es de 1 440 km/h y 1 180 km/h respectivamente. Supónganse que a 45°N se envía una bola hacia el Sur (sobre el mar galileano congelado, es decir, sin fricción) a una velocidad de 4 km/h. Analicemos la situación al llegar a los 30°N: la Tierra tiene en ese punto una velocidad hacia el Este (respecto del espacio absoluto) de 1 440 km/h, pero la del móvil es de sólo 1 180 km/h (con la que partió). Es decir; la bola ha "adquirido" una tremenda velocidad lateral —de unos 260 km/h— que la desvía hacia el Oeste, es decir, hacia la derecha.
Es muy fácil ver que ocurre lo mismo si el móvil va de los 30°N a los 45°N: nuevamente se observa, desde la Tierra, un fabuloso desvío hacia la derecha. El mismo análisis en el hemisferio meridional predice un desvío hacia la izquierda. Esta es la explicación del efecto de Coriolis en la horizontal.
2) Desviación de la vertical. Este fenómeno es mucho más fácil de entender y explicar: en el corto tiempo que la piedra tarda en caer desde la punta del mástil, la Tierra ha girado un poco y por lo tanto el objeto no aterriza exactamente en la base del mástil.
![[FNT 10]](../img/i9ap29.jpg)
3) Péndulo de Foucault. Para entender este tercer fenómeno, imaginémonos al mencionado péndulo colgado de un soporte ideal situado exactamente sobre el Polo Norte. En la figura siguiente, se indica a la derecha su plano de oscilación con un rectángulo dibujado sobre el globo terráqueo en la parte izquierda. Que el soporte sea "ideal" quiere decir que no le imprime al péndulo el movimiento de rotación de la Tierra. Luego, una observadora que no gire con la Tierra (es decir, que esté fija al espacio absoluto) ve oscilar el péndulo siempre en el mismo plano. Es la Tierra la que gira bajo el péndulo y es por eso que, para una persona fija al planeta, el plano de oscilación parece estar girando lentamente (hacia el otro lado).
Las tres explicaciones anteriores tienen varias cosas en común: en primer lugar son clásicas, sobre todo la 1 y la 3; pueden ustedes consultar su enciclopedia o texto de (geo) física o geografía, y lo más probable es que encuentren una explicación muy similar. (Las aquí expuestas para los casos 1 y 3 fueron tomadas, casi literalmente, de un libro de texto de oceanografía física; la del 2, apareció en un libro de divulgación de mecánica.) En segundo lugar, las tres explicaciones muestran el efecto de Coriolis como algo aparente, producto del hecho que hacemos observaciones desde un planeta en rotación, de nuestro carácter de terrícolas. En tercero y último lugar —pero no por eso menos importante— las tres explicaciones expuestas arriba son incorrectas; más precisamente, las dos primeras son totalmente erróneas, mientras que la tercera es una "no explicación".
El péndulo de Foucault en el Polo Norte
Puede parecer una pérdida de tiempo haber presentado estas tres "explicaciones" para inmediatamente derribarlas, pero tuve un par de razones para hacerlo. Por un lado son muy frecuentes y por lo tanto estoy corrigiendo un error común. Por el otro, la razón por lo que estas tres explicaciones —y algunas similares— fallan es precisamente porque insisten en presentar el fenómeno como algo aparente; la confusión entre realidad y apariencia tiene una historia muy larga, como veremos más adelante. Uno de los motivos que me llevó a escribir este libro fue contar esta historia y tratar de aclarar esa confusión.
Con el fin de poder criticar estas explicaciones —y entender el resto de este libro— es importante hacer una distinción precisa entre la experiencia de una observadora fija al espacio absoluto newtoniano (que ve girar la Tierra) y la de un observador fijo a nuestro planeta (que lo percibe quieto, y ve, en cambio, girar todo el firmamento a su alrededor). Para distinguirlos, llamaré a la primera observadora inercial y al segundo terrícola; es importante recordar esta nomenclatura en lo que sigue. Invito al lector a regresar a las tres explicaciones anteriores y determinar cuándo se habla de una observadora inercial y cuándo de un terrícola.
Asimismo, a lo largo de este libro diré que un fenómeno es aparente cuando es percibido por un terrícola en su carácter de tal, pero no por una observadora inercial. La denominación de real, por el contrario indicará un fenómeno que es percibido tanto por terrícolas como por observadores inerciales. Por ejemplo, la rotación del Sol alrededor de la Tierra es un fenómeno aparente, mientras que el invierno y verano son reales (¡y vaya si lo son!). El cambio de luminosidad y temperatura entre la noche y el día ¿es real o aparente?
Paso a argumentar por qué son erróneas las tres explicaciones.
1) Desviación en la horizontal. La explicación 1 "predice" correctamente el sentido de la deflexión, hacia la derecha en el hemisferio septentrional y hacia la izquierda en el meridional; sin embargo, es incorrecta pues falla en lo que se refiere a la forma de la trayectoria y a la rapidez con que la recorre.
Si una partícula es impulsada hacia el Sur; desde los 45°N, con una velocidad de 4 km/h (como el ejemplo), la desviación hacia la derecha es tan fuerte que se mueve en un círculo de 11 km de radio (una décima de grado de meridiano); ¡está muy lejos de llegar a los 30°N, que queda unos 1 700 km al sur! Además, lo que es muy importante, la rapidez con que se mueve es siempre la misma, es decir, sigue moviéndose a 4 km/h, sin alcanzar velocidades absurdas como 260 km/h.
Este comportamiento se llama oscilación inercial y es resultado exclusivo del efecto de Coriolis, en ausencia de fuerzas horizontales, de fricción u otras. La trayectoria tiene —para los terrícolas— la forma de un círculo en todos los casos en que el impulso sea suficientemente débil para que el móvil no se acerque demasiado al ecuador.
El tiempo en que el móvil recorre este "círculo inercial" es igual a medio día dividido por el seno de la latitud. En el ejemplo anterior; este periodo es igual 12 horas/sen (45°) = 17 horas; a una velocidad de 4 km/h en este tiempo el móvil recorre una circunferencia de 68 kilómetros, correspondiente a un radio de 11 km. En el capítulo IV presentaré una descripción más completa de las oscilaciones inerciales, incluyendo dibujos de las trayectorias sobre la Tierra.
Entonces un terrícola ve al objeto moverse en un círculo de 11 kilómetros cerca de 45°N. Si el efecto de Coriolis fuera sólo aparente, ¿cómo lo vería una observadora inercial? lo debería ver seguir un círculo máximo, ya que ésta es la trayectoria en ausencia del efecto de Coriolis, como bien predijo Galileo. Esto no ocurre, ya que si se moviera en un círculo máximo debería cruzar el ecuador: el efecto de Coriolis es real, no aparente. Los demás capítulos de este libro están dedicados a explicar sus causas y narrar la historia de quién fue el que realmente lo descubrió; la explicación de los puntos 2 y 3 estará en cambio limitada a lo que resta del presente capítulo.
2) Desviación de la vertical. No resistí a la tentación de presentar la explicación 2, porque es errónea no sólo cuantitativamente sino también cualitativamente: ¡incluso el signo que lleva no está bien colocado! (La 1 "al menos" lo tiene bien puesto, aunque de todos modos sea incorrecta.) Según 2, una observadora inercial ve a la piedra moviéndose sólo en dirección al centro de la Tierra. Si esto fuera cierto, un terrícola la vería aterrizar hacia el Oeste del lugar donde fue arrojada (no al Este, como predice el efecto de Coriolis) y ¡a una distancia enorme!
Por ejemplo, supóngase que la piedra es arrojada desde unos 50 metros de altura.
Esto significa que tardará unos tres segundos en llegar al suelo,5
![[Nota 5]](../img/mcommnt.gif) tiempo en el cual un punto del ecuador ha recorrido un kilómetro y medio. Si
fuera cierta la "explicación" 2 ¡sería bastante diferente jugar al tenis! (entre
otras cosas). En realidad, la ausencia de este resultado absurdo —el hecho
de que los cuerpos dejados caer no llegan al suelo a cientos de metros del lugar
donde fueron arrojados— fue invocado durante muchos siglos por los defensores
de la cosmología de Ptolomeo —o sea, los opuestos a la de Copérnico—
como un argumento en contra de la rotación terrestre.
tiempo en el cual un punto del ecuador ha recorrido un kilómetro y medio. Si
fuera cierta la "explicación" 2 ¡sería bastante diferente jugar al tenis! (entre
otras cosas). En realidad, la ausencia de este resultado absurdo —el hecho
de que los cuerpos dejados caer no llegan al suelo a cientos de metros del lugar
donde fueron arrojados— fue invocado durante muchos siglos por los defensores
de la cosmología de Ptolomeo —o sea, los opuestos a la de Copérnico—
como un argumento en contra de la rotación terrestre.
Newton fue aparentemente el primero en conjeturar —no demostrar—
que la piedra debía caer un poco hacia el Este, con base en el siguiente razonamiento:
consideremos una torre, su base y su cúspide junto con todo lo demás fijo a
la Tierra) se mueven hacia el Este, pero la punta lo hace un poquito más rápido
que la base, ya que está un poquito más lejos del eje de rotación de la Tierra.
Por ejemplo, en el caso de la Torre de Pisa6![[Nota 6]](../img/mcommnt.gif) la diferencia de velocidad es igual a tres milímetros por segundo (unos escasos
diez metros por hora o aproximadamente el doble de la velocidad de crucero
de un caracol) en los tres segundos y fracción que tarda en llegar al suelo
una piedra dejada a caer en la punta, este impulso horizontal representa un
desplazamiento de un centímetro hacia el Este.
la diferencia de velocidad es igual a tres milímetros por segundo (unos escasos
diez metros por hora o aproximadamente el doble de la velocidad de crucero
de un caracol) en los tres segundos y fracción que tarda en llegar al suelo
una piedra dejada a caer en la punta, este impulso horizontal representa un
desplazamiento de un centímetro hacia el Este.
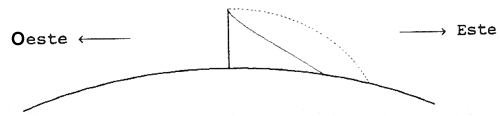
Desviación al este en caída libre (línea llena,)
Predicción incorrecta de Newton (línea cortada)
Newton le sugirió a Robert Hooke7![[Nota 7]](../img/mcommnt.gif) hacer el experimento de dejar caer bolas desde una torre, sin darles ningún
impulso y, verificar que cayeran un poco hacia el Este de la posición original.
Con este experimento se convencería a los escépticos que no creían todavía en
la rotación terrestre. En respuesta a la sugerencia de Newton, Hooke señaló
correctamente que debía haber también una deflexión hacia el Sur (como fue explicado
más arriba) y dijo haber hecho exitosamente el experimento. Sin embargo, no
es posible que lo haya logrado en forma decisiva, ya que la desviación predicha,
como se señaló más arriba, es demasiado pequeña.
hacer el experimento de dejar caer bolas desde una torre, sin darles ningún
impulso y, verificar que cayeran un poco hacia el Este de la posición original.
Con este experimento se convencería a los escépticos que no creían todavía en
la rotación terrestre. En respuesta a la sugerencia de Newton, Hooke señaló
correctamente que debía haber también una deflexión hacia el Sur (como fue explicado
más arriba) y dijo haber hecho exitosamente el experimento. Sin embargo, no
es posible que lo haya logrado en forma decisiva, ya que la desviación predicha,
como se señaló más arriba, es demasiado pequeña.
El razonamiento de Newton corresponde a la curva discontinua en la figura anterior...
y es incorrecto; la verdadera trayectoria es la de la curva llena. Para entender
este resultado teórico curioso (aunque difícil de medir) hay que primero darse
cuenta de que, mientras cae, la piedra no es afectada por la rotación terrestre:
se halla en órbita alrededor del centro de masa de la Tierra, del mismo modo
que los planetas están en órbita alrededor del Sol. Si el lector conoce la segunda
ley de Kepler8 ![[Nota 8]](../img/mcommnt.gif) sabrá
que al acercarse al centro de la Tierra, la piedra debe aumentar la velocidad
angular total, es decir; la combinación de la observada por un terrícola
y la debida a la rotación terrestre. Al acercarse al centro de la Tierra —es
decir, al caer— la piedra gira cada vez un poquito más rápido que el planeta
sobre su eje, y es por eso que cae un poquito hacia el Este. Se puede ver que
el desplazamiento respecto de la base de la torre es 2/3 del predicho por el
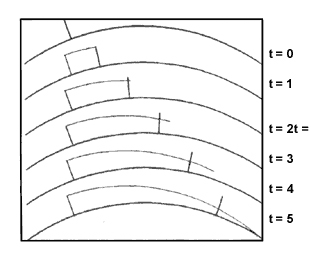
razonamiento de Newton. En la siguiente figura se puede apreciar el movimiento
de la torre y el objeto desde el punto de vista de una observadora inercial
en diferentes instantes, hasta que éste llega a la Tierra. La línea de puntos
indica la posición original de la torre y la curva fina la trayectoria recorrida
por el objeto hasta ese instante.
sabrá
que al acercarse al centro de la Tierra, la piedra debe aumentar la velocidad
angular total, es decir; la combinación de la observada por un terrícola
y la debida a la rotación terrestre. Al acercarse al centro de la Tierra —es
decir, al caer— la piedra gira cada vez un poquito más rápido que el planeta
sobre su eje, y es por eso que cae un poquito hacia el Este. Se puede ver que
el desplazamiento respecto de la base de la torre es 2/3 del predicho por el
razonamiento de Newton. En la siguiente figura se puede apreciar el movimiento
de la torre y el objeto desde el punto de vista de una observadora inercial
en diferentes instantes, hasta que éste llega a la Tierra. La línea de puntos
indica la posición original de la torre y la curva fina la trayectoria recorrida
por el objeto hasta ese instante.
Movimiento de la torre y el objeto en caída libre, vistos por una observadora en reposo
3) El péndulo de Foucault. El punto 3 es una "no explicación" porque presenta al fenómeno precisamente en el único lugar donde no hay ningún efecto real (un polo). Imagínense que deseo explicarles a los habitantes de Planolandia (los que, como es bien conocido carecen de la dirección vertical) el "fenómeno de la caída de los cuerpos", es decir, la observación de que si suelto un objeto desde una cierta altura, luego de un cierto tiempo (que depende de dicha altura) llega al piso. Si "por ser más fácil" eligiera para ilustrar el fenómeno, el caso particular en que la altura es nula (es decir, cuando apoyo el cuerpo en el suelo) estaría cometiendo un error similar de "no explicación"; al igual que, en el punto 3, el caso límite corresponde a una situación ¡donde no ocurre el efecto a explicar!
El hecho de que en los polos la rotación terrestre no afecte al péndulo de Foucault, no explica en absoluto por qué su plano de oscilación gire —para un terrícola— como lo hace en los museos de ciencia. Por ejemplo, la rapidez con que gira el plano es igual a una vuelta diaria por el seno de la latitud del lugar donde esté montado el péndulo. ¿Es esto un efecto aparente? No; una observadora inercial no ve al plano de oscilación fija (salvo en el caso muy especial del polo), sino que lo ve girando alrededor de la vertical local, la cual a su vez rota en torno al eje terrestre. Esto no es un movimiento aparente sino real y complicado, producido por fuerzas reales. Más adelante regresaré al péndulo de Foucault y a discutir cuáles son las fuerzas que producen su curioso movimiento.
La desviación de la vertical —en la caída libre— es un efecto demasiado
pequeño y difícil de observar.9 ![[Nota 9]](../img/mcommnt.gif) También
es ínfimo el efecto con respecto al péndulo de Foucault, sólo que en este caso
hay más tiempo para que se acumule un resultado tangible: se necesitan cientos
de oscilaciones del péndulo para que pueda observarse un cambio de la orientación
del plano. La caída libre, en cambio, ocurre demasiado rápido para que la corrección
sea apreciable.
También
es ínfimo el efecto con respecto al péndulo de Foucault, sólo que en este caso
hay más tiempo para que se acumule un resultado tangible: se necesitan cientos
de oscilaciones del péndulo para que pueda observarse un cambio de la orientación
del plano. La caída libre, en cambio, ocurre demasiado rápido para que la corrección
sea apreciable.
Las oscilaciones inerciales constituyen otro ejemplo donde transcurre el tiempo suficiente para que el efecto de Coriolis sea apreciable. De hecho, este tipo de movimiento es observado muy frecuentemente en el océano, sobre todo tras un cambio brusco de la dirección del viento.
Por otra parte, otro fenómeno —como el de la caída libre— donde tampoco
hay tiempo suficiente para que se pueda observar normalmente el efecto de Coriolis
es el del vórtice del desagüe, con el que comencé este capítulo.10
![[Nota 10]](../img/mcommnt.gif) Allí,
el sentido de giro es determinado por las peculiaridades del recipiente. El
que el agua rote siempre en la misma dirección (y que ésta sea diferente en
cada hemisferio) es sólo un mito sin fundamento, que demuestra la escasa capacidad
de observación de la agente.
Allí,
el sentido de giro es determinado por las peculiaridades del recipiente. El
que el agua rote siempre en la misma dirección (y que ésta sea diferente en
cada hemisferio) es sólo un mito sin fundamento, que demuestra la escasa capacidad
de observación de la agente.
Espero haberlos convencido de que las tres "explicaciones" presentadas dos son incorrectas y una insuficiente. Todavía no he dado la explicación correcta; para hacerlo, tengo antes que platicar de otros temas. Empiezo insistiendo en el tema de la realidad y la apariencia.
![[Inicio]](../img/begin.gif)
![[Anterior]](../img/prevsec.gif)

![[Siguiente]](../img/nextsec.gif)
![[FNT 9]](../img/i8p28.jpg)
![[FNT 11]](../img/i9bp29.jpg)
![[FNT 14]](../img/i12p35.jpg)