II. LÁSERES DE ALTA POTENCIA

INTERACCIÓN ÁTOMO-FOTÓN

El romance entre la radiación y la materia

LA FIGURA II.1 muestra esquemáticamente la estructura básica de un átomo de acuerdo con el modelo de Bohr. Podemos ver que éste consta esencialmente de un núcleo alrededor del cual giran electrones en determinadas órbitas. Como vimos en el capítulo anterior, el modelo de Bohr mostró que un electrón no se puede encontrar en cualquier órbita alrededor de un núcleo, sino sólo alrededor de determinadas órbitas estables y que los intercambios de energía son cuantizados. Además de esto, la energía de un electrón en una órbita se incrementa entre mayor sea la órbita en que se encuentra. De este modo, en la figura II.2 se muestra la energía correspondiente a cada una de las órbitas mostradas en la figura II.1. Podemos notar que la órbita de menor energía es la primera órbita; cuando el átomo se encuentra en esta situación decimos que se encuentra en su estado base o estado de menor energía. Debido a la diferencia de energía entre cada órbita tenemos que, para pasar de una órbita inferior a una superior (por ejemplo, de la segunda a la tercera órbita), se debe recibir un cuanto de energía, es decir, una cantidad de energía exactamente igual a la diferencia de energía entre esas dos órbitas; mientras que si se pasa de una órbita superior a una inferior (por ejemplo, de la cuarta a la tercera órbita), el átomo debe emitir un cuanto de energía. Por otra parte, también podemos apreciar en la figura II.1 que hay un límite superior a la energía que un electrón puede adquirir. Pasando ese límite ya no hay órbitas superiores que sobrepasar y entonces el electrón queda libre, dejando un átomo ionizado, es decir, un átomo que ha perdido uno o varios de sus electrones.

Figura II. 1.

Figura II. 2.

El considerar los procesos de interacción entre radiación electromagnética y materia en su más pequeña escala se reduce a estudiar la interacción entre cuantos de energía y átomos. Estos cuantos de energía también se conocen como fotones. Por simplicidad consideraremos átomos con sólo dos niveles de energía: uno inferior de energía E₁ y uno superior de energía E₂.

La figura II.3 muestra el proceso de absorción en el cual un fotón incide en un átomo que inicialmente se encuentra en su estado base o no excitado. En este caso, y suponiendo que la energía del fotón sea idéntica a la diferencia de energía entre los dos niveles del átomo (lo cual siempre supondremos), tenemos como resultado que éste absorbe la energía del fotón incidente, pasando por tanto de su estado base a su estado excitado de mayor energía.

Figura II. 3.

La figura II.4 muestra el proceso de emisión. En este caso un átomo inicialmente excitado de manera espontánea pasa a un estado de menor energía, emitiendo en el proceso un fotón con energía igual a la diferencia de energía entre los dos niveles. El fotón se emite en una dirección totalmente arbitraria.

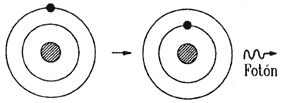
Figura II.4.

La figura II.5 muestra el proceso de emisión estimulada, cuya existencia fue propuesta por Albert Einstein en 1917, y es el proceso fundamental gracias al cual existe el láser. En este proceso se tiene la interacción entre un fotón y un átomo que inicialmente se encuentra en un estado excitado. Como resultado de esta interacción el átomo pasa a su estado base, emitiendo en el proceso un fotón que tiene las mismas características de dirección y de fase que el fotón inicial. Cuando esto último ocurre decimos que la radiación electromagnética resultante es coherente. Es importante notar que en este proceso está ocurriendo realmente un proceso de amplificación de fotones, pues inicialmente tenemos sólo un fotón y después del proceso de emisión estimulada tenemos como resultado dos fotones. Podemos afirmar que el germen que dio origen al desarrollo del láser surgió cuando el fenómeno de emisión estimulada fue propuesto. De hecho la palabra láser es el acrónimo de la expresión en inglés: Light Amplification by Stimulated Emission of Radiation, que en español podemos traducir como "amplificación de la luz por la emisión estimulada de radiación".

Figura II. 5.

ABSORCIÓN Y AMPLIFICACIÓN ÓPTICA

De la creación y aniquilación de fotones

Debemos ahora considerar la interacción no entre un átomo y un fotón, sino entre una gran cantidad de fotones y un gran número de átomos desde una perspectiva más real. La figura II.6 muestra una cavidad en la que se encuentran N átomos de los cuales una cantidad N₂ son átomos que están en su estado excitado y N₁ son átomos que se encuentran en su estado base o no excitado. Al propagarse un flujo S de fotones a través de la cavidad y entrar en interacción con átomos que están excitados, ocurrirá el proceso de emisión estimulada. Como hemos visto, este proceso traerá como consecuencia la amplificación del flujo inicial de fotones S. Esto se debe a que, como ya sabemos, cada fotón de flujo incidente que interactúe con un átomo inicialmente excitado dará origen, por medio del proceso de emisión estimulada, a la emisión de un segundo fotón junto con la transición del átomo del estado excitado al estado base o no excitado. Sin embargo, debido a que en dicha cavidad también hay átomos que se encuentran en su estado base, al interactuar el flujo de fotones con estos átomos ocurrirá el proceso de absorción de fotones y ocasionará una disminución del flujo inicial S de fotones. Esto se debe a que cada fotón que interactúe inicialmente con un átomo en su estado base, será absorbido por dicho átomo y éste pasará a un estado excitado.

En la práctica debemos considerar simultáneamente los procesos de emisión y de absorción. El primero tiende a amplificar el flujo incidente dependiendo de la cantidad de átomos que se encuentren en el nivel superior N₂, mientras que el segundo tiende a disminuir el flujo incidente dependiendo de la cantidad de átomos que se encuentren en el nivel base N₁. Al considerar de manera simultánea los dos procesos, el resultado final depende de la cantidad de átomos que se encuentran tanto en el estado excitado como en el estado base. Si estas cantidades son iguales; tendremos entonces que, en promedio, la amplificación y la absorción que sufre el pulso inicial son iguales, y por tanto el flujo final no será ni mayor ni menor que el flujo de fotones inicialmente incidente. Esto es, si

N₂ = N₁,

el cambio neto del flujo de fotones es cero, es decir, la cantidad de fotones que sale de la cavidad cilíndrica mostrada en la figura II.6 es la misma que la que entró.

Figura II. 6.

Por otra parte, si el número de átomos excitados N₂ que hay en la cavidad es menor que el número de átomos en su estado base N₁, el resultado promedio total será de una reducción del flujo inicial de fotones. Esto es, si

N₂ < N₁,

el flujo inicial de fotones será absorbido. Ello implica que a lo largo de su propagación por la cavidad cilíndrica mostrada en la figura II.6, el flujo inicial de fotones disminuye como se muestra en la figura II.7.

Figura II. 7.

Finalmente, si el número de átomos excitados N₂ que hay en la cavidad es mayor que el número de átomos en estado base N₁, el resultado promedio total será de un incremento al flujo inicial de fotones. Es decir, si

N₂ > N₁,

el flujo inicial de fotones se incrementará a lo largo de su propagación por la cavidad cilíndrica mostrada en la figura II.6. El flujo de fotones es entonces ampliado por el medio, como se muestra en la figura II.8.

Figura II. 8.

AMPLIFICADORES ÓPTICOS

La reproducción fotónica

Con lo antes mencionado podemos ahora comprender la operación de un amplificador óptico, también conocido como amplificador láser. Este es un sistema que proporciona a la salida un flujo final de fotones S_f mayor que el flujo inicial S_i. Dichos amplificadores ópticos generalmente tienen un aspecto similar al mostrado en la figura II.6, es decir, cilíndrico. Por un extremo entra un flujo inicial de fotones y por otro sale el flujo final de fotones amplificado.

Como vimos en la sección anterior, la condición necesaria para tener amplificación del flujo inicial de fotones S₁, es que el número de átomos excitados N₂ que se encuentra en la cavidad amplificadora sea mayor que el número de átomos que se encuentra en su estado base N₁. La condición anterior se conoce como inversión de población y el problema central para la realización práctica de un amplificador óptico está en cómo lograrla. Es decir, el problema es conseguir que la mayoría de los átomos que se encuentra en la cavidad amplificadora pase de su estado base, que es el estado normal en que cualquier átomo se encuentra cuando no es perturbado, a un estado excitado.

Para lograr dicha inversión de población es necesario algún dispositivo que proporcione la energía que los átomos de la cavidad amplificadora requieren para pasar de su estado base a un estado excitado. Este dispositivo recibe el nombre de sistema de bombeo y puede ser de varios tipos, aunque los más usuales son de tipo óptico o de tipo eléctrico.

Lo que se tiene en el caso de un sistema de bombeo de tipo óptico es la cavidad amplificadora circundada por una o varias lámparas luminosas de destello flash muy potentes. Al ser disparadas dichas lámparas, los fotones que emiten son absorbidos por los átomos de la cavidad amplificadora, los cuales pasan de su estado base a un estado excitado. Con ello se logra la inversión de población. La figura II.9 muestra la sección transversal de dos posibles arreglos para colocar las lámparas flash en un amplificador bombeado ópticamente.

Figura II. 9.

En un sistema de bombeo de tipo eléctrico se produce una intensa descarga eléctrica en los átomos que se encuentran en la cavidad amplificadora. De este modo, los energéticos electrones de la descarga transfieren parte de su energía por colisiones electrón-átomo a los átomos contenidos en la cavidad, logrando que éstos pasen de su estado base a uno excitado. Así se da la inversión de población. La figura II.10 muestra la sección transversal de un amplificador óptico bombeado eléctricamente, usando un cañón de electrones.

Figura II. 10.

Para amplificar un pulso de luz usando un amplificador óptico dotado de un sistema de bombeo óptico o eléctrico, se sincroniza el paso del pulso de luz con el disparo del sistema de bombeo. Es importante que estos dos hechos estén perfectamente sincronizados, pues si el sistema de bombeo se dispara antes o después de que llegue el pulso de luz al amplificador, este pulso no será amplificado. La figura II.11 muestra la simulación computacional de la amplificación de un pulso de luz que pasa a través de un amplificador óptico. Pueden observarse el pulso inicial y el pulso final amplificado.

Figura II. 11.

OSCILADOR ÓPTICO

El creador del rayo láser

Después de haber expuesto el principio básico de operación de un amplificador óptico, podemos comprender fácilmente el principio de funcionamiento de un oscilador óptico, también conocido como oscilador láser, o sencillamente láser.

Consideremos una cavidad amplificadora con un sistema de bombeo (representado por las flechas perpendiculares en la figura II.12), a la cual hemos colocado en sus extremos un par de espejos planos (o ligeramente cóncavos) tal como ahí se muestra, donde la línea punteada indica el eje óptico del sistema. Este par de espejos paralelos recibe el nombre de resonador óptico. Uno de los espejos del resonador es casi 100% reflejante, y el otro tiene una reflectancia que es de manera característica de alrededor de 90 por ciento.

Figura II. 12.

Para comprender qué función tiene el resonador óptico nos remitiremos a la figura II.13, la cual muestra al oscilador óptico inmediatamente después de que el sistema de bombeo fue disparado. Cualquier fotón que sea emitido en una dirección diferente de la definida por el eje óptico del resonador óptico se perderá, mientras que cualquier fotón emitido a lo largo del eje óptico del oscilador será amplificado por el proceso de emisión estimulada. Inmediatamente se generará un enorme flujo de fotones confinados por el resonador óptico, que se propagarán a lo largo del eje óptico. Si el resonador óptico no estuviera allí, después de disparar el sistema de bombeo los átomos que fueron excitados pasarían a su estado base debido al proceso de emisión espontánea, emitiendo fotones en todas direcciones y perdiendo la energía recibida por el sistema de bombeo.

Figura II. 13.

La presencia del resonador óptico nos permite extraer de modo eficiente la energía que el sistema de bombeo ha depositado en los átomos contenidos en la cavidad amplificadora. Debido a que uno de los espejos del resonador tiene reflectancia de 90%, el 10% de los fotones que incide allí será trasmitido fuera del resonador óptico, formando un haz de luz muy intenso, que además es monocromático (formado por fotones de idéntica energía), coherente (pues todos sus fotones están en fase, ya que fueron producidos por el proceso de emisión estimulada) y altamente direccional. Estas son las propiedades fundamentales de la luz láser que es generada por todo oscilador óptico.

PRODUCCIÓN DE PULSOS LÁSER ULTRACORTOS

Los fotones trabajando juntos

Como hemos visto, al excitar por medio de un pulso óptico o eléctrico el medio activo en un resonador óptico, podemos producir un pulso láser. La duración de este pulso es, en general, similar a la del pulso de excitación y característicamente es entre 500 y 1 000 microsegundos. Para muchas aplicaciones prácticas, como la fusión nuclear vía láser, o para la soldadura o el corte de placas de acero, la duración de tales pulsos es muy grande y su intensidad demasiado pequeña. Debido a esto se han diseñado varias técnicas que permiten obtener pulsos láser de muy corta duración y de muy alta intensidad. Una de las técnicas más empleadas para producir pulsos ultracortos de alta intensidad se conoce como conmutación de Q.

En todo sistema físico que presente oscilaciones, desde un columpio hasta un láser, se define una cantidad llamada factor de calidad, que se denota por la letra Q. Si el valor de Q en un láser es pequeño implica que en la cavidad láser se tienen muchas pérdidas ópticas, mientras que si el valor de Q es grande implica que casi no hay pérdidas en la cavidad.

La figura II.14 muestra un oscilador óptico con altas pérdidas, es decir, con un bajo valor de Q. Las pérdidas en este caso son producidas al introducir un "objeto extraño" en el interior del resonador óptico que impide que el sistema entre en oscilación y que el proceso de amplificación estimulada pueda ser eficiente. Por otra parte, la figura II.13 muestra un oscilador óptico con bajas pérdidas y por tanto con un alto valor de Q. En este último caso no hay nada que impida la oscilación óptica del sistema.

Figura II. 14.

Es posible construir un oscilador óptico que contenga en el interior de su resonador un interruptor óptico que nos permita variar a voluntad el valor Q de la cavidad. Esto se muestra en la figura II.15. Si el interruptor está encendido, el flujo de fotones puede pasar a través de él y esto nos da un alto valor de Q. Por otro lado, si el interruptor está apagado, el flujo de fotones no puede atravesarlo y tenemos entonces un bajo valor de Q.

Figura II. 15.

Si el interruptor óptico está apagado (o sea, un bajo valor de Q) y simultáneamente se dispara el sistema de bombeo, el sistema no puede entrar en oscilación láser y por lo tanto no puede perder energía emitiendo radiación láser hacia el exterior. Por tanto, toda la energía depositada por el sistema de bombeo será asimilada por los átomos contenidos en la cavidad amplificadora. Así, casi todos los átomos pasarán a su estado excitado y muy pocos permanecerán en su estado base. Por tanto, el nivel de inversión de población que se define como la diferencia N₂ — N₁, alcanzará un valor muy grande. Si en este momento —en el que tenemos un muy alto valor de inversión de población—, repentinamente encendemos el interruptor óptico (obteniéndose así un alto valor de Q) el sistema entrará violentamente en oscilación y muy pronto se generará un corto e intenso pulso de luz láser. Esto se muestra en la figura II.16. Allí podemos ver el bajo valor inicial de Q. El disparo del sistema de bombeo se inicia produciendo un incremento en el valor del nivel de inversión de población. En el instante t_i en que se acciona el interruptor óptico y se tiene un alto valor de Q, el nivel de inversión de población rápidamente decrece, produciéndose un corto e intenso pulso de luz láser. Algunos valores característicos de duración y potencia de pulsos láser generados mediante esta técnica son del orden de 10 x 10^-9 segundos de duración y entre 1 x 10⁶ y 1 x 10⁸ watts de potencia. Sin embargo, existen sistemas láser para lograr la fusión nuclear que pueden alcanzar potencias de hasta 20 x 10¹² watts (ñ20 giga watts!) en pulsos de 1 nanosegundo (1 x 10^-9 segundos).

Figura II. 16.

LÁSERES PARA FUSIÓN

La llave de la fusión

Para realizar investigación sobre fusión vía láser se han construido varios láseres en el mundo. El cuadro II.1 muestra algunos de los más importantes así como sus parámetros técnicos. Dentro de las características más importantes en la elección de un láser para este tipo de aplicaciones destacan la duración de los pulsos láser producidos, su energía, la longitud de onda de operación (el color de la luz emitida) y el número de haces láser disponibles para ser simétricamente focalizados en el blanco (que son las microesferas con mezcla de deuterio y tritio). Cada una de estas características es importante para mejorar diferentes aspectos del proceso de fusión; esto lo veremos con más detalle en el próximo capítulo. Sin embargo, por el momento podemos adelantar que la longitud de onda l del láser es una de las más importantes. De hecho, para lograr el proceso de fusión, entre más corta sea l mejor.

CUADRO II. 1.
País	Láser	Laboratorio	Energía/duración de pulso	Haces láser	Longitud de onda mm
EUA	Nova	Livermore	70 KJ/2.5 nseg.	10	0.35
	Omega	Rochester	3 KJ/1 nseg.	24	0.35
	Chroma	Kms fusión	0.7 KJ/1 nseg.	2	0.53
Japón	Gekko XII	Osaka	15 KJ/1 nseg.	12	0.53
Francia	Luli	Ecole Poly	0.7 KJ/0.6 nseg.	6	1.06
		Palaiseau	0.2 KJ/0.5 nseg.		0.25
Gran Bretaña	Vulcan Helen	Rutherford Aldermaston	3 KJ/1 nseg. 1.3 KJ/0.2 nseg.	12 3	0.53
Rusia	Delfin	Lebedev	3 KJ/1 nseg.	108	1.06
China	Shenguan	Shanghai	2 KJ/1 nseg.	2	1.06
Italia	—	Frascati	0.2 KJ/3 nseg.	2	1.06

La siguiente lista muestra algunos láseres pulsados de alta energía y potencia así como sus longitudes de onda característicos de operación:

Láser de CO2	10.6 mm
Láser de CF3I	1.31 mm
Láser de neodimio	1.06 mm (o 0.35 mm)
Láser de rubí	0.69 mm
Láser de KrF	0.24 mm

Por razones técnicas y económicas casi todos los sistemas láser construidos en el mundo para aplicación en fusión por láser son de neodimio. Los sistemas láser de bióxido de carbono (CO₂), a pesar de su alta eficiencia (mayor a 15%), prácticamente no se utilizan debido a su larga longitud de onda de emisión; los láseres de rubí tampoco se usan debido a que resultan demasiado caros, pues el rubí es un cristal muy costoso de producir. Los únicos competidores actuales de los láseres de neodimio son los de CF₃I y los de KrF; sin embargo, los problemas técnicos de construcción y operación de estos láseres (que, por ejemplo, requieren del manejo de sustancias altamente corrosivas) son mayores que los del neodimio.

La figura II.17 muestra el diagrama simplificado del láser Vulcan del laboratorio Rutherford Appleton en Didcot, Inglaterra. Ahí se tiene el más importante sistema láser de Europa para investigación en fusión. La mesa del oscilador contiene un láser cuya función es proporcionar pulsos con perfiles temporal y espacial determinados. Los pulsos láser ahí obtenidos son de baja intensidad y es necesario amplificarlos. Esto se hace pasando cada pulso a través de una serie de amplificadores, denotados como A16, A25, A32 y A45. Estos amplificadores son barras de neodimio de 16, 25, 32 y 45 milímetros de diámetro. En esta misma figura podemos identificar aisladores ópticos, que operan variando la polarización de los pulsos láser, denotados como WP y FR, e interruptores ópticos como PC. Para corregir defectos y optimizar el perfil de intensidad transversal de los pulsos láser producidos se usan filtros que se denotan como AP y VSF. Finalmente, como DA se encuentra un conjunto de amplificadores de disco de 108 y 150 mm de diámetro. Estos amplificadores de disco son amplificadores láser que no consisten en barras sólidas de neodimio sino de discos de neodimio con dos a tres centímetros de espesor. Separados entre sí, cuatro o seis de estos "discos" (que de hecho son en forma elíptica), se colocan en cada tubo amplificador. Este diseño de amplificador tiene la ventaja de que su enfriamiento después de cada disparo láser es más rápido y eficiente de lo que sería usando una barra sólida de neodimio de igual diámetro.

Figura II. 17.

Ahora que en el primer capítulo ya hemos descrito lo que es la fusión nuclear, mientras que en éste vimos el tipo de láseres que utilizan en la investigación de fusión por láser, en el siguiente capítulo veremos cuál es el efecto de focalizar estos intensos pulsos láser en la materia para así producir fusión nuclear.