VI. LA CONTRIBUCI�N DE FARADAY A LA TEOR�A DE DISOCIACI�N ELECTROL�TICA
|
JOS� L. C�RDOVA F
|
RESUMEN |
Se presentan los antecedentes cient�ficos y filos�ficos
que llevaron a Faraday a proponer la disociaci�n electrol�tica en los
t�rminos del modelo de Boscovich. Se analizan y discuten someramente
los conceptos y experimentos cient�ficos que permitieron a Svante Arrhenius
proponer, basado en la contribuci�n de Faraday, la Teor�a de Disociaci�n
Electrol�tica. El trabajo concluye mencionando que las investigaciones
de Faraday contribuyeron indirectamente al nacimiento de la fisicoqu�mica
como ciencia. |
EN 1850, nueve a�os antes de que naciera Arrhenius, 17 antes de
que muriera Faraday, el Journal of the Royal Agricultural Society of England
public� dos art�culos 13 ![[Nota 13]](../img/mcommnt.gif)
que
describ�an el fen�meno del intercambio i�nico en los terrenos de cultivo. En
uno de ellos se mencionaba que el cloruro de potasio pod�a ser retenido por
el terreno a pesar de las lluvias. El dispositivo experimental empleado para
comprobarlo era muy sencillo: una caja con tierra y perforaciones en el fondo.
Al analizar el l�quido que sal�a de la caja despu�s de verter soluci�n de cloruro
de potasio, se encontr� que conten�a cloro pero nada de potasio; �ste hab�a
sido reemplazado por calcio y magnesio.
Hoy d�a se representa lo anterior con:
Ca2 + 2K+ (del terreno).
La explicaci�n, como toda aquella de car�cter cient�fico, es resultado de la colaboraci�n de muchos cient�ficos. En este trabajo se intenta ilustrar el papel que en ello tuvieron dos de ellos: Faraday y Arrhenius.
En tiempos de Faraday (1820) era del dominio cient�fico la existencia de dos tipos de electricidad, originalmente llamados v�trea y resinosa. Las reacciones qu�micas se pod�an explicar entonces en t�rminos de atracci�n y repulsi�n el�ctricas. As�, los polos de un circuito atra�an a distancia los componentes de una mol�cula, destruy�ndola.
EL MODELO DE DISOCIACI�N DE FARADAY
Michael Faraday not� experimentalmente que no era suficiente la cercan�a de los polos el�ctricos para producir una reacci�n qu�mica: hac�a falta una descarga el�ctrica. De una manera semejante hab�a hallado que no se pod�a magnetizar agujas met�licas con polos el�ctricos sino que se necesitaba una descarga. El experimento al que nos referimos consisti� en colocar un papel filtro humedecido con soluci�n de yoduro de potasio entre dos terminales cargadas el�ctricamente. Cuando se libera yodo, el papel toma su caracter�stico color violeta, de forma que era f�cil comprobar si hab�a tenido lugar una reacci�n qu�mica. Sin embargo, repetimos, no bastaba la cercan�a de los polos: deb�a producirse una descarga el�ctrica para liberar el yodo.
A fin de interpretar el fen�meno, Faraday propuso que los componentes de las mol�culas de yoduro de potasio emigraban en direcciones opuestas intercambiando continuamente de pareja hasta transformarse en especies qu�micas libres en los polos; la corriente el�ctrica produc�a una perturbaci�n a trav�s de la soluci�n qu�mica, que llevaba a la liberaci�n de yodo.
Igual que su maestro H. Davy, Faraday conoc�a los trabajos de Gowin Knigth y del jesuita Roger Boscovich, cuyas obras capitales tienen t�tulos muy reveladores. La del primero es: Intento de demostrar que todos los fen�menos en la naturaleza pueden explicarse por dos principios activos simples: atracci�n y repulsi�n; y la de Boscovich: Teor�a de filosof�a natural elaborada segun la �nica ley de las fuerzas existentes en la naturaleza.
La unidad y convertibilidad de las fuerzas resultaba m�s consistente a las convicciones religiosas de Faraday, de manera que acept� el modelo de Boscovich, del que se hablar� a continuaci�n.
EL MODELO AT�MICO DE BOSCOVICH
Boscovich elabor� en 1758 un modelo at�mico que combinaba las fuerzas de atracci�n y repulsi�n de manera que el patr�n de fuerzas de un �tomo boscovicheano ser�a como el que se muestra en la figura VI. 1.
La fuerza entre los �tomos resultaba repulsiva a ciertas distancias y atractiva a otras. N�tese que, a distancias grandes, la fuerza era atractiva, de acuerdo con la ley de la gravitaci�n de Newton; adem�s, cada punto de intersecci�n de la curva con el eje X representaba un punto de equilibrio, necesario para la existencia de compuestos qu�micos.
El modelo at�mico de Boscovich part�a de unas cuantas suposiciones y bastaba un solo tipo de part�culas para explicar la gran diversidad de sustancias, y emplear, adem�s, una sola curva de fuerza interat�mica; con ello, las fuerzas qu�micas y gravitacionales se reduc�an a una sola. Como podr� suponerse, este modelo era puramente cualitativo; no se hab�an desarrollado instrumentos, ni experimentales ni matem�ticos como para hacer predicciones cuantitativas.
![[FNT 13]](../img/136-94.gif)
Figura VI.1. Modelo at�mico de Boscovich.
Ya se mencion� que la adhesi�n de Faraday al �tomo de Boscovich tuvo ra�ces ideol�gicas. La doctrina de la unidad y convertibilidad de las fuerzas de la naturaleza (la Naturephilosophie alemana del siglo XIX) contradec�a al materialismo ingl�s y ofrec�a un lugar al mundo del esp�ritu. Faraday era un hombre muy religioso y es probable que optara por el modelo boscovicheano porque hallaba en �l m�s coherencia con la creaci�n de Dios, quien no dejar�a a los �tomos materiales en interacci�n ca�tica.
Seg�n el modelo de Boscovich, los compuestos qu�micos eran agregados de �tomos cuyas propiedades eran resultado de patrones de fuerzas de part�culas puntuales. Si se permite el anacronismo, los �tomos deb�an entenderse como interpenetraciones de campos de fuerza. Seg�n esto, los �tomos de Faraday no eran bolas de billar atractivas o repulsivas, sino centros de un complejo nudo de fuerzas.
Volviendo a la disociaci�n del yoduro de potasio, la explicaci�n que Faraday propuso fue la transmisi�n de una vibraci�n gracias a la interacci�n de los �tomos; en vista de que las fuerzas entre los �tomos eran atractivas a unas distancias y repulsivas a otras, la perturbaci�n se trasmit�a en la soluci�n hasta producir yodo libre.
La aportaci�n de Faraday a la teor�a de disociaci�n electrol�tica se puede resumir en los siguientes puntos:
1) El cambio qu�mico se debe al paso de electricidad y no a la simple atracci�n el�ctrica.
2) El cambio qu�mico se da en los electrodos. S�lo scuando el ion yodo llega al electrodo se transforma en �tomo de yodo.
3) El paso de la corriente el�ctrica se debe a un intercambio de part�culas de distinta carga: los iones.
Debe subrayarse que, para Faraday los iones eran producidos por la diferencia de potencial el�ctrico. Como se ver� m�s adelante, Arrhenius propuso que para formar iones bastaba con la disoluci�n de una sal en agua, sin necesidad de polos el�ctricos.
Aproximadamente en 1857, Rudolph Clausius postul� que en una soluci�n exist�a un peque�o n�mero de iones producidos por las colisiones azarosas de las mol�culas. Puesto que en una soluci�n, como en los gases, las part�culas se mueven a muy diferentes velocidades, era posible que algunas tuvieran suficiente energ�a como para romper las mol�culas del compuesto en una colisi�n. Seg�n Johann Wilhelm Hittorf las part�culas resultantes de estas colisiones transportaban la carga el�ctrica en las soluciones, y eran los iones de Faraday.
Svante Arrhenius consider� las ideas anteriores al formular su teor�a de disociaci�n electrol�tica que present� en su tesis de doctorado (Universidad de Uppsala, 1884). No es ocioso decir que esta tesis recibi� comentarios muy poco elogiosos por parte de sus profesores. Uno de ellos, Per Theodor Cleve (descubridor de los elementos holmio y tulio), afirmaba:
...no tiene ning�n sentido decir que en una soluci�n
de cloruro de potasio el cloro y el potasio est�n separados el uno del
otro... |
Arrhenius propon�a que al disolver el cloruro de potasio en agua, los iones cloro y potasio se formaban sin necesidad de corriente el�ctrica. Para entonces, la idea que prevalec�a al respecto entre los qu�micos era la de Faraday: los iones se producen por el paso de la corriente el�ctrica a trav�s del electrolito; precisamente la palabra electrolito significa "destruido por la electricidad".
A pesar de las oposiciones, la tesis de Arrhenius fue aprobada pero no se le autoriz� para ser profesor de la universidad.
Obviamente no era Suecia el lugar donde pod�a consolidarse la teor�a, de modo que Arrhenius escribi� a Rudolf Clausius, Lothar Meyer, Wilhelm Ostwald y Jacobus van't Hoff y les envi� copias de su tesis. El entusiasmo e influencias de Ostwald y Van't Hoff ayudaron a difundir la teor�a de Arrhenius, a pesar de la oposici�n de cient�ficos de la talla de Mendeleyev, Kahlenberg y Lodge. El rechazo lleg� a darse en t�rminos tan acres como los de Lodge:
el senor Arrhenius es demasiado generoso en la
manipulaci�n de datos imaginarios...de esta forma logra una enorme confusi�n
de la cual puede obtener sus llamadas deduciones te�ricas. |
Sir Oliver Lodge sugiri�, con 50 a�os de anticipaci�n, la emisi�n solar de ondas de radio.
Ahora bien, entrando en materia, los experimentos hechos por Arrhenius para su tesis investigaban la conductividad de electrolitos empleando un depolarizador desarrollado poco antes. Este consist�a en un conmutador manual que permit�a cambiar el sentido de la corriente el�ctrica varias veces por segundo, de manera que se evitaba la acumulaci�n de cargas y, por consiguiente, la heterogeneidad de la soluci�n. En otras palabras, con esta t�cnica Arrhenius logr�, por primera vez, mediciones confiables de la conductividad de electrolitos.
Arrhenius trabaj� adem�s con soluciones muy diluidas (del orden de 5 x 10-4 equivalentes/litro), de manera que pudo llegar a conclusiones muy originales (aunque no totalmente fundamentadas). Por ejemplo:
1) Para soluciones muy diluidas, la conductividad espec�fica de una soluci�n salina es aproximadamente proporcional a su concentraci�n en id�nticas condiciones.
2) La conductividad de una soluci�n diluida de dos o m�s sales es igual a la suma de las conductividades que tendr�an las soluciones de cada sal a la misma concentraci�n.
3) La conductividad de una soluci�n es igual a la suma de las conductividades de soluto y solvente.
4) Si no se observan estas leyes esto se debe a que hay acci�n qu�mica entre soluto y solvente.
5) La resistencia el�ctrica aumenta con el peso molecular del solvente.
Hoy d�a la quinta conclusi�n se considera incorrecta: la resistencia el�ctrica aumenta con la constante diel�ctrica del soluto (no con el peso molecular). Sin embargo, para las sustancias que Arrhenius emple� (agua, alcoholes, �teres), la constante diel�trica aumenta con la masa molar.
La importancia de la tesis de Arrhenius, con todo, no radica tanto en las mediciones experimentales cuanto en las ideas que al respecto comenz� a elaborar. Por ejemplo:
A estas part�culas submoleculares las llam� iones, empleando el mismo t�rmino que Faraday. Como mencionamos antes, la proposici�n de una parte activa y otra inactiva ya la hab�a hecho Clausius al afirmar que los choques entre las part�culas pod�an romper las mol�culas. N�tese, por otro lado, que la formulaci�n de Arrhenius empleaba el concepto de equilibrio qu�mico para explicar el comportamiento de las soluciones acuosas.
Continuemos con la tesis de Arrhenius:
...el calor de neutralizaci�n liberado por la transformaci�n
de una base perfectamente activa y un �cido perfectamente activo es
s�lo el calor de actividad del agua, donde el calor de actividad es
el calor empleado para transformar una sustancia del estado inactivo
al activo. |
El lector habr� observado que "perfectamente activo" significa completamente disociado, y que la reacci�n entre una base fuerte y un �cido fuerte es, simplemente:
Experimentalmente se encuentra que DH� es independiente de la naturaleza del �cido y la base, lo cual apoya fuertemente a la teor�a de la disociaci�n de Arrhenius. En efecto si DH� es constante es porque, posiblemente, siempre se tienen los mismos reactantes y los mismos productos. Considerando al �cido fuerte HA y la base fuerte BOH; si �stos, como afirma Arrhenius, est�n disociados completamente, dan lugar a:
y la reacci�n de neutralizaci�n es:
En resumen: la reacci�n de un �cido fuerte y una base fuerte es, simplemente, la reacci�n (1) y, en consecuencia, existen iones H + y OH- en soluci�n sin necesidad de corriente el�ctrica.
A fin de explicar las variaciones experimentales Arrhenius defini� un "coeficiente de actividad" igual al cociente del n�mero de iones realmente contenido en la soluci�n y el n�mero de iones que habr�a si el electrolito se transformara completamente en iones. Dicho de otra manera: mientras m�s fuerte fuese un �cido, base, etc., mayor ser�a su coeficiente de actividad y, de acuerdo con las ecuaciones de equilibrio qu�mico, el coeficiente de actividad en la diluci�n infinita. Obviamente, las soluciones que emple� Arrhenius estaban muy diluidas (aproximadamente 5 x 10-4 equivalentes/litro).
Arrhenius tambi�n consider� la ley de migraci�n i�nica independiente de Kohlrausch:
donde L es la conductividad equivalente, m+,- es un coeficiente de proporcionalidad (llamado "movilidad i�nica") y a es el "coeficiente de actividad" introducido por Arrhenius (hoy conocido como "grado de disociaci�n").
Cuando Kohlrausch inici� su investigaci�n acerca de la capacidad de las soluciones para conducir corriente el�ctrica, el tema era asunto de una gran controversia. Por ejemplo, se discut�a la validez de la ley de Ohm para las soluciones, pues los resultados eran poco consistentes. Como se mencion�, la �nica corriente el�ctrica disponible en el laboratorio era corriente continua, la cual produce polarizaci�n en los electrodos e influye en las mediciones, por Arrhenius se evit� ese problema utilizando un depolarizador.
Tambi�n influ�an en las mediciones el tiempo empleado (pues se calentaba la soluci�n), la intensidad de la corriente (afectaba la homogeneidad de la soluci�n); sin embargo, a pesar de estas dificultades se pudo llegar a relaciones emp�ricas valiosas. Por ejemplo, la gr�fica de conductividad equivalente de un electrolito (L) contra la ra�z cuadrada de la concentraci�n en equivalentes/litro (�c), de la figura VI.2 es, para unas sustancias, una recta, mientras que para otras es una curva. Las sustancias que dan lugar a rectas fueron llamadas "electrolitos fuertes" por su gran reactividad qu�mica: HCl, KOH, KCl. Las otras como el CH3COOH, fueron nombradas "electrolitos d�biles". Para los electrolitos fuertes, cuya gr�fica es una recta, se pueden hacer extrapolaciones para diluci�n infinita; sin embargo, para los electrolitos d�biles la extrapolaci�n es poco precisa. El punto anterior es muy importante porque el comportamiento de una soluci�n muy diluida es m�s predecible que el de una concentrada, pues las interacciones de las part�culas del soluto son bajas.
![[FNT 14]](../img/136_99.gif)
Figura VI.2. Conductividad equivalente vs /c
En 1876 Kohlrausch pudo se�alar que en soluciones muy diluidas los iones tienen
un movimiento independiente de su pareja. En una soluci�n diluida cada especie
electroqu�mica tiene una conductividad propia. (cuadro VI.1).15 De
hecho Kohlrausch propon�a que la conductividad de la soluci�n era igual a la
suma de las conductividades de los componentes:
Se emplea L� para indicar conductividad a diluci�n infinita, pues en este caso la concentraci�n de soluto es igual a cero.
El cuadro VI.1 muestra las conductividades de algunos electrolitos fuertes
a diluci�n infinita16 y
D representa la diferencia entre las conductividades
de dos soluciones con un ion com�n, por ejemplo:
pero por la proposici�n de Kohlrausch:
En el cuadro VI.1 se ve que el resultado loK+ - lo Li+ es independiente de las sales empleadas.
En el p�rrafo anterior se se�al� la dificultad de determinar L, pues la curvatura de la l�nea hace poco confiable la extrapolaci�n; sin embargo, la ley de Kohlrausch permite calcular L0 para el �cido ac�tico.
Kohlrausch encontr� c�mo cuantificar una propiedad caracter�sfica de las especies qu�micas que intervienen en el transporte de corriente en una soluci�n. Esta propiedad es independiente del compuesto del cual procede y, evidentemente, no es afectada por el ion de carga opuesta. Sin embargo, para poder afirmar que los iones tienen existencia aun sin la corriente el�ctrica hac�an falta los trabajos de Raoult y las aportaciones te�ricas de Clausius y Van't Hoff, que fueron sintetizados de manera elegante y completa por Arrhenius.
|
|
||
|
L0
|
||
|
Electrolito
|
Conductividad (m2 /ohm)
|
D = l0K+
- l0Li+
|
|
|
||
| KCl |
0.014986
|
|
| LiCl |
0.011503
|
3.483 X 10-3 |
|
|
||
| KClO4 |
0.014004
|
|
| LiClO4 |
0.010598
|
3.406 X 10-3 |
|
|
||
|
L0
|
D = l0Cl- - l0(NO3)- | |
| LiCl |
0.01503
|
|
| LiNO3 |
0.011010
|
4.93 x 10-4 |
|
|
||
| KCl |
0.014986
|
|
| KNO3 |
0.014498
|
4.90 x 10-4 |
|
|
||
| HCl |
0.042616
|
|
| HNO3 |
0.042130
|
4.83 x 10-4 |
|
|
||
LAS PROPIEDADES COLIGATIVAS Y LA TEOR�A DE ARRHENIUS
Por los trabajos de Clemens Heinrich von Babo (1847) y Adolf Wullner (1856) era un hecho conocido que la presi�n de vapor de un solvente disminu�a al agregar un soluto y que dicha disminuci�n era aproximadamente proporcional al peso del soluto. Desde tiempos de Fahrenheit se hacia uso de este efecto: �l mismo lo emple� (en 1722) para definir uno de los puntos de referencia de su escala termom�trica: la temperatura de fusi�n de una soluci�n de sal y agua. Fahrenheit hab�a notado tambi�n el aumento en la temperatura de ebullici�n por la presencia de un soluto.
Obviamente, en las observaciones de Fahrenheit, de Von Babo o de Wullner no se inclu�a a la masa molar del soluto, pues no se hab�a desarrollado este concepto. Por otro lado, al experimentar con sustancias electrol�ticas se obten�an resultados poco consistentes, como se explicar� m�s adelante.
Francois Marie Raoult, por el contrario, emple� principalmente sustancias org�nicas (que generalmente son no electrol�ticas) para investigar las propiedades de las soluciones (presi�n de vapor, temperaturas de ebullici�n y congelaci�n). Encontr� que los cambios en esas propiedades eran aproximadamente proporcionales al peso del soluto (1880). Ya con el desarrollo del concepto de masa molar, Raoult pudo hallar que la disminuci�n del punto de congelaci�n de cualquier soluci�n de concentraci�n 1 g en 100 g de agua, multiplicada por la masa molar, era una constante
|
|
||||||
|
0.001 molal
|
0.01 molal
|
0.1 molal
|
||||
|
Dtteor
|
Dtexp
|
Dtteor
|
Dtexp
|
Dtteor
|
Dtexp
|
|
|
|
||||||
| C12H22O11 | 0.00186 | 0.00186 | 0.0186 | 0.0186 | 0.186 | 0.186 |
| NaCl | 0.00186 | 0.00366 | 0.0186 | 0.0360 | 0.186 | 0.348 |
| K2SO4 | 0.00186 | 0.00528 | 0.0186 | 0.0501 | 0.186 | 0.432 |
| K3Fe(CN)6 | 0.00186 | 0.00710 | 0.0186 | 0.0626 | 0.186 | 0.530 |
|
|
||||||
Esta relaci�n se pod�a aplicar tambi�n a la temperatura de ebullici�n y a la presi�n del vapor. Sin embargo, cuatro a�os m�s tarde Raoult report� que esa relaci�n fallaba con electrolitos, pero se aplicaba a los radicales que compon�an las sales como si �stos estuvieran separados en la soluci�n.
Raoult emple� la ecuaci�n 4 para determinar las masas molares de az�cares y alcoholes, sin embargo no investig� el origen de las desviaciones de las sales, ejemplificados en el cuadro VI. 2.
La ecuaci�n 4 puede rearreglarse considerando que implica concentraci�n de 1 g por 100 g de agua:
......................................................................= k2..............................(constante), (5)
.m2
y dividiendo la ecuaci�n 4 entre la 5, obtenemos
......m1 .........k2
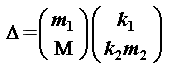
donde n es el n�mero de moles de part�culas de solutos y k3 una constante.
Es interesante observar que el valor Dtteor para las tres sales se aproxima a Dtexp cuando se multiplica respectivamente por 2, 3 y 4, respectivamente. Si el valor de Dt es funci�n del n�mero de part�culas, como lo sugiere la ecuaci�n 6, la conclusi�n ser� que hay 2, 3 y 4 veces el n�mero te�rico de part�culas.
|
|
|||
|
molalidad =
|
0.001
|
0.01
|
0.1
|
|
|
|||
| NaCL |
1.97
|
1.94
|
1.87
|
| MgSO4 |
1.82
|
1.53
|
1.21
|
| K2SO4 |
2.84
|
2.69
|
2.32
|
| K3Fe(CN)6 |
3.82
|
3.36
|
2.85
|
|
|
|||
El mismo problema encontr� Van't Hoff al investigar la presi�n osm�tica de soluciones electrol�ticas; para resolverlo ide� un coeficiente emp�rico i que correg�a los resultados te�ricos (Cuadro VI.3).
De hecho ambos t�rminos i y a, est�n relacionados por la estequiometr�a de la reacci�n
A+ +B-.........................................................(7)
En efecto, si consideramos la reacci�n 7 como reversible y en equilibrio qu�mico, el n�mero total de part�culas (n ) en la soluci�n es:
donde c� es la concentraci�n molar inicial de la soluci�n, y a el coeficiente de actividad de Arrhenius, es decir:
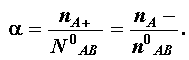
Los valores experimentales de i y a + 1 fueron tan aproximados que Arrhenius no titube� en hablar de disociaci�n a fin de explicar las anomal�as en las propiedades coligativas. Para ello bastaba atribuir diferentes grados de disociaci�n a las soluciones, lo que depend�a de la naturaleza y concentraci�n de las especies qu�micas.
Tomando como ejemplo una soluci�n 1 M de NaCl, cuya temperatura experimental de congelaci�n es -3.39� C, si se considera la reacci�n de disociaci�n total:
habr� el doble de part�culas en soluci�n (una concentraci�n 2 M) y una temperatura de congelaci�n te�rica de -3.72� C, mayor que el valor experimental. Arrhenius propuso que la reacci�n de disociaci�n de la sal es reversible:
Na+ + Cl-;
en ella el equilibrio qu�mico entre las tres especies produce un n�mero menor de part�culas que el debido a una disociaci�n total. Como puede verse en el cuadro VI.2, al disminuir la concentraci�n de la soluci�n de NaCL, el coeficiente emp�rico i se acerca a 2.
Sin embargo, �c�mo admitir que aumenta el n�mero de part�culas en una sal sin una corriente el�ctrica?, �c�mo explicar que una part�cula de Cl en la soluci�n tenga propiedades f�sicas y qu�micas tan diferentes a las del cloro gaseoso? Tales fueron las principales objeciones a la teor�a de Arrhenius la cual, sin embargo, pudo explicar:
a) las anomal�as de la temperatura de congelaci�n de electrolitos,
b) la diferencia entre electrolitos fuertes y d�biles,
c) las anomal�as en los valores de la presi�n osm�tica de los electrolitos,
d) las anomal�as en la temperatura de ebullici�n de electrolitos,
e) el valor constante del calor de neutralizaci�n de �cidos y bases fuertes.
f) la variaci�n en la presi�n de vapor de las soluciones electrol�ticas.
En una carta a Van't Hoff (30 de marzo de 1877), Arrhenius presentaba un razonamiento similar al presentado en este trabajo. La respuesta de Van't Hoff fue:
Su carta me ha aclarado considerablemente la constituci�n
de las soluciones. Puesto que los electrolitos se descomponen en sus
iones, el coeficiente i debe estar entre 1 y el n�mero correspondiente
a la disociaci�n. Con toda probabilidad los electrolitos se disocian
completamente en diluciones extremas. |
Sin embargo, a pesar de dar una interpretaci�n elegante a una gran diversidad de fen�menos, la teor�a de Arrhenius encontr� muchas oposiciones. Como se�alamos, Per Theodor Cleve, sinodal en el examen doctoral de Arrhenius, argumentaba que las cargas opuestas del cloro y del potasio imped�an la separaci�n de los iones. Arrhenius respond�a que la atracci�n entre los iones era vencida por la de las mol�culas del disolvente a los iones; si los iones no estaban hidratados (solvatados), no pod�an existir separados. Cleve preguntaba: �c�mo pod�a existir cloro en una soluci�n incolora e inofensiva de KCI siendo que el cloro es un gas amarillo verdoso y altamente oxidante?, �c�mo pod�a existir potasio en tal soluci�n sin liberar hidr�geno?
Hoy d�a tales preguntas parecen triviales (m�s por la familiaridad de los t�rminos que por la comprensi�n de los conceptos); sin embargo, debe recordarse que en 1884 a�n no se hab�a descubierto el electr�n. S�lo 16 a�os m�s tarde, con el concepto de electr�n, pudo explicarse el origen de la carga el�ctrica de los iones y la diferencia sustancial entre un �tomo y su ion.
Si bien hay diferencias notables entre las teor�as de disociaci�n de Faraday y la de Arrhenius no puede dejar de mencionarse la influencia de Faraday. Esta va m�s all� del concepto de ion como part�cula el�ctrica: incluye el intento de unificaci�n de fen�menos el�ctricos y magn�ticos, de fen�menos f�sicos y qu�micos.
El valor de ambas teor�as no radica s�lo en la belleza con que explicaron hechos aparentemente inconexos sino, sobre todo, porque permitieron plantear nuevos experimentos y leyes. La influencia de Faraday, a trav�s de Arrhenius, llev� a la creaci�n de una nueva disciplina: la fisicoqu�mica.
Concluyamos se�alando que las objeciones y rechazos a la teor�a de Arrhenius fueron explicados por �l mismo cuando recibi� el premio Nobel de qu�mica 1903.
La nueva teor�a tuvo la mala suerte de que nadie
sab�a d�nde ubicarla: ni los qu�micos en la qu�mica, ni los f�sicos
en la f�sica. Se tuvo que construir un puente entre ambas ciencias. |
C�rdova, J. L. "Equivalente qu�mico". Contactos, vol. II, n�m. 6, 1985, pp. 44-52.
C�rdova, J. L. "Teor�a de disociaci�n electrol�tica. Un enfoque hist�rico". Contactos, vol. III, n�m. 1, 1987, pp. 28-35.
Coulston, G. Dictionary of Scientific Biography. Ch. Scribner's Sons, Nueva York, 1976.
![[Inicio]](../img/begin.gif)
![[Anterior]](../img/prevsec.gif)
![[Siguiente]](../img/nextsec.gif)