V. FARADAY Y LA NOCIÓN DE VACÍO
|
LUIS DE LA PEñA
|
CUANDO se piensa en el desarrollo de la física a lo largo del siglo XIX, es frecuente imaginarlo como un proceso continuo y apacible, carente de las violentas rupturas que caracterizaron a las primeras décadas de nuestro siglo. Sin embargo, es un hecho que durante el siglo pasado surgieron al menos dos vertientes de la física, de naturaleza netamente revolucionaria. La primera de ellas, cronológicamente hablando, surgió con la incorporación a la física de la hipótesis de los químicos sobre la estructura corpuscular de la materia y su posterior desarrollo y aplicación, por ejemplo, a la teoría cinética de los gases y al redireccionamiento de la investigación hacia los fenómenos de escala atómica.
Para percibir las dificultades que el modelo atómico tuvo que superar para
su aceptación general, baste recordar que investigadores de la talla de Ostwald,
el creador de la físico- química —por no traer a colación el ejemplo usual
de Mach—, todavía en el presente siglo aceptaban los átomos a lo más como
un modelo útil pero carente de realidad física; o bien, que se requirió un siglo
completo para transformar la hipótesis de Dalton en una teoría física comprobada
—lo que ocurrió con los trabajos sobre el movimiento browniano de Einstein
(y Smoluchowski) y su ulterior verificación experimental por Perrin y sus discípulos,
periodo que va de 1905 a 1915, aproximadamente—2![[Nota 2]](../img/mcommnt.gif)
lo que permitió sustituir la convicción dominante hasta entonces, derivada de
la física clásica y newtoniana y firmemente reforzada por la teoría electromagnética,
de la materia como un continuo, por la de su estructura granular.
La segunda ruptura epistemológica a que hicimos mención se refiere a lo que viene a ser; indudablemente, la mayor contribución conceptual de la física de varios siglos, y no sólo del XIX: la introducción del concepto de campo como un ente físico de nivel ontológico, equivalente al que goza la materia. Es difícil exagerar la importancia de este descubrimiento, no sólo para el estudio de fenómenos no mecánicos como los electromagnéticos, sino para nuestra comprensión general de la estructura y naturaleza del mundo físico. En las siguientes páginas trataremos de repasar someramente algunos de los momentos centrales del proceso intelectual que permitió llegar a la noción de campo electromagnético que nació con los trabajos pioneros de Michael Faraday (1791-1867), y de describir cómo es que esta búsqueda se liga profundamente con la respuesta a otra pregunta milenaria: ¿qué es y cómo es el vacío?
FARADAY Y SUS LÍNEAS DE FUERZA
A partir de sus observaciones experimentales de fenómenos magnéticos, Faraday llegó a la convicción de que éstos se dan en la región del espacio que rodea a los cuerpos magnetizados —y algo similar ocurre con los electrizados— por lo que no se trata de acciones a distancia, sino de efectos transmitidos por las líneas de fuerza que él consideraba algo así como el camino o el vehículo de las acciones magnéticas. Detengámonos en un par de comentarios para aclarar las ideas.
El primero se refiere a la noción misma de línea de fuerza. Faraday partía
de una concepción de la materia dentro de la tradición atomista de Boscovich,
Bernoulli, Dalton, Davy —su mentor—, etc., considerándola formada
por centros puntuales, a los que convergen las líneas de fuerza.3
Las
líneas de fuerza representan para Faraday un estado de esfuerzos y deformaciones
que se da en el espacio entre los átomos. Faraday tiende a considerarlas como
una sustancia, sujeta a los esfuerzos correspondientes y transmisora
de ellos; esta sustancia se distingue de la materia común y sus diferentes estados
deberían permitir explicar todas las fuerzas entre los cuerpos. Esta
idea conduce a Faraday a convencerse de que debe ser posible transformar unas
fuerzas en otras, e incluso unificarlas en una sola. De aquí deriva Faraday
su convicción de que debería existir alguna relación entre la luz y la electricidad
con el magnetismo, lo que logró verificar finalmente con el descubrimiento del
efecto Faraday, que consiste en la modificación del plano de polarización
de la luz por un imán.
Más tarde, en 1844, para evitar las paradojas a que conduce la noción de acción a distancia, Faraday propuso considerar que cada átomo está conectado a cualquier otro a través de líneas de fuerza, por lo que la acción de éstas se extiende sobre todo el espacio. Así, desapareció para Faraday la noción de espacio vacío, que no necesitaba de un éter transmisor de las acciones eléctricas o magnéticas: la sustancia de la fuerza permea todo el espacio y el interior de la materia común. Argumentó que, en todo caso, las líneas de fuerza podrían corresponder, alternativamente, a algún estado de éter, como una vibración o una tensión, etc., por lo que el medio magnético en el espacio podría ser el propio éter. En cualquiera de estas formas, estamos en presencia de una concepción campal del fenómeno magnético que se abre paso, por vez primera, en la descripción de los fenómenos físicos.
La teoría de la gravitación universal elaborada por Newton considera que la
fuerza gravitatoria entre los cuerpos celestes actúa de manera instantánea e
independiente del medio (o espacio) entre tales cuerpos. Esta concepción influenció
largamente el pensamiento físico y prevalecía aún a mediados del siglo pasado;
fue aceptada por autores tan importantes como Ampñre. La preocupación central
de Faraday desde 1821, año en que inicia sus investigaciones sobre la electricidad
y el magnetismo, es precisamente la verificación de su hipótesis alternativa
—o especulación, como él la llama— de que las acciones eléctricas
y magnéticas son progresivas y requieren tiempo para propagarse. Por
ejemplo, logró demostrar que la inducción magnética —fenómeno descubierto
por él mismo— no es una acción a distancia, sino el resultado de que se
cortan líneas de fuerza (sea por movimiento entre conductor e imán, sea porque
se haga cambiar la corriente en un conductor, con los cuerpos fijos).4
La noción de un éter que llena el espacio —incluyendo los intersticios de la materia y sus átomos— es tan antigua como el pensamiento materialista griego; entre los griegos, el éter era la quinta esencia, más fundamental aún que los cuatro elementos que creían que daban cuerpo a la materia y que era quizá la materia del alma. A este éter se le consideraba material y atómico y, para Lucrecio, su movimiento generaba el movimiento de los astros. Con la noción newtoniana de espacio absoluto y la teoría ondulatoria de la luz, propuesta por Newton —que la consideraba complemento indispensable de su teoría corpuscular de la luz— Hooke, y especialmente Huygens y sus sucesores, reaparece en la física la noción de éter —ahora como éter luminífero—, como la sustancia en que se asientan las vibraciones de las ondas luminosas. En esta visión, el éter es a la luz lo que el aire al sonido o el océano a las olas. Más aún que en Faraday, la posición de Newton respecto del éter es ambivalente, aunque su tendencia es negarlo (por ejemplo, en la segunda edición de su Opticks, 1706) o, en todo caso, mantenerlo explícitamente como una hipótesis.
DE MAXWELL A EINSTEIN: LOS CAMPOS CLÁSICOS
Como hemos visto, a Faraday lo atrae, más que el éter, la idea del espacio en sí mismo permeado por la sustancia que él considera fundamental, el medio o la sustancia magnética o eléctrica; concibe las líneas de fuerza como estados del espacio —y esto debería poder extenderse a la luz y a la gravedad— y no considera que sea necesario el éter para que puedan existir tales líneas, aunque tampoco se resiste a admitirlo si fuera necesario, si bien su esquema no lo necesita. Maxwell (1831-1879) inició sus investigaciones sobre la electricidad y el magnetismo en 1861, partiendo de las nociones de Faraday. Igual que su predecesor, interpretó las líneas de fuerza como estados de esfuerzos y deformaciones, pero de un éter mecánico y newtoniano. Maxwell fue muy lejos con este modelo, en combinación con el método de analogías: consideró un modelo mecánico del éter en términos de celdas rotatorias (los vórtices), separadas entre sí por esferitas giratorias que evitan la fricción, modelo que según él, posee un comportamiento análogo al de los fenómenos eléctricos y magnéticos que estaba investigando.
La analogía resultó tan acabada, que le permitió deducir las ecuaciones correctas para los fenómenos electromagnéticos. Por ejemplo, encontró que en analogía a los cambios en el desplazamiento de las celdas elementales generados por los esfuerzos, debía introducir una corriente de desplazamiento asociada a la variación de los campos eléctricos en los medios dieléctricos. Este es quizá el descubrimiento específico más importante de Maxwell, pues de él depende la posibilidad de existencia de las ondas electromagnéticas. Este ejemplo muestra el inmenso valor heurístico que las analogías tuvieron en las manos de Maxwell para establecer las leyes del electromagnetismo.
En la descripción original de Maxwell, los fenómenos electromagnéticos quedan
representados por campos asociados al fluido etéreo: campos de velocidad,
de esfuerzos, etc.5 En
esta forma llegó a sus ecuaciones del electromagnetismo como una teoría de campo,
en la que las líneas de fuerza son esfuerzos sobre el éter magnético —que
distinguía cuidadosamente de su modelo, el éter de los vórtices—.
Los fenómenos electromagnéticos se propagan, según esta teoría, como en un medio
elástico, es decir, con velocidad finita, Maxwell descubrió que era muy cercana
a la de la luz. Esta observación le permitió identificar a la luz como una onda
electromagnética y simplificar el esquema, proponiendo que su éter y el luminífero
eran la misma cosa. Sin embargo, cada vez se alejaba más de las concepciones
originales de Faraday; por ejemplo, encontró que los campos eléctricos y magnéticos
se propagaban en dirección ortogonal a las líneas de fuerza, por lo que éstas
no podían concebirse ni como trayectorias ni como vehículos de los correspondientes
efectos, como proponía Faraday.
Hacia 1864, Maxwell dio el paso definitivo: aceptó las acciones electromagnéticas como un campo, al que se propone describir sin recurrir a modelos o analogías circunstanciales; en su Tratado de electricidad y magnetismo, ve ya al campo electromagnético como un sistema dinámico, generado por la materia en movimiento, y poseedor de propiedades físicas como energía, momento, etc., que antes de Maxwell eran atributo exclusivo de la materia ponderable. Sin embargo, pese a asignarle tales atributos sustanciales, Maxwell mantuvo al campo electromagnético aún en un nivel ontológico diferente al de la materia, pues no lo trató como una sustancia, sino como estado de una sustancia, el éter luminoso.
Con todo ello, el establecimiento por Maxwell de la teoría electromagnética,
que engloba los fenómenos eléctricos, magnéticos y ópticos en un cuerpo teórico
unificado, permanece hasta nuestros días como una de las grandes proezas del
intelecto humano. La comprobación por Heinrich Hertz (1857-1894) de la existencia
real de las ondas electromagnéticas o hertzianas predichas por Maxwell, además
de unificar definitivamente la óptica y el electromagnetismo,6 abrió
a la humanidad una gama de nuevas posibilidades científicas y tecnológicas de
gran importancia y vastedad —especialmente en las comunicaciones—
comparables con las que los grandes descubrimientos de Faraday introdujeron
con el uso generalizado de la energía eléctrica.
Desde el punto de vista del desarrollo de la noción de campo, el continuador tal vez más significativo de la obra de Maxwell fue Hendrik Antoon Lorentz (1853-1928). Este investigador holandés, que llegaría a convertirse en un patriarca de la física teórica, partió de la hipótesis de que la materia está hecha de moléculas cargadas (iones) que interaccionan entre sí vía el éter, el cual, sin embargo, permanece invariablemente inmóvil. Como el éter actua sobre los iones —a través de la fuerza ponderomotriz o fuerza de Lorentz—, pero éstos no actúan sobre aquél por el requerimiento de inmovilidad, el éter de Lorentz resulta un sistema dinámico no newtoniano, que viola la ley de acción y reacción. Pronto (en 1892), Lorentz se convenció de que el campo electromagnético mismo —el estado del éter no-newtoniano— tampoco era un sistema newtoniano en su teoría.
Alrededor de 1890, Lorentz se encontró con una contradicción dentro de la teoría de la luz que requirió una solución insólita. Desde tiempo atrás se sabía que la aberración de la luz —es decir, la desviación angular de la luz que nos llega de las estrellas— se podía explicar adecuadamente mediante la teoría de Fizeau (1819-1896), que se deduce de suponer que el éter excesivo, en el interior de la materia, es arrastrado por ésta en su movimiento en el espacio cósmico. Sin embargo, los elegantes experimentos de Albert Michelson (1852-1931) y sus colaboradores demostraron, sin lugar a dudas, que no hay movimiento relativo éter-Tierra. La única salida que encontró Lorentz a esta dificultad para su teoría del éter móvil consistió en inventar una contracción ad hoc de los cuerpos en la dirección de su movimiento respecto del éter. Esta es la famosa contracción de Lorentz, propuesta simultáneamente por el físico irlandés George Fitzgerald (1851-1901) y redescubierta poco tiempo después, desde perspectivas muy diferentes, por el matemático y filósofo francés Henri Poincaré (1854-1912) y por el joven Einstein. Para Lorentz esta contracción era un fenómeno real, de origen dinámico aunque no newtoniano, debida, pensaba inicialmente, al cambio de la fuerza entre el éter y los iones producido por el movimiento; más tarde la supuso generada por el cambio en las dimensiones de los electrones en movimiento respecto del éter.
Lorentz jamás renunció a la idea del éter sustancial e inmóvil y a la concepción del campo electromagnético como un estado de dicho éter no newtoniano, ni aun frente al advenimiento de la teoría de la relatividad que asignara a su contracción y a la respectiva transformación temporal —también dependiente de la velocidad y que para Lorentz era un mero cambio de variable, carente de contenido físico— un carácter fundamental. El cambio cualitativo se da con la intervención de Einstein (1879-1955) en el asunto.
Desde muy joven, Einstein se sintió atraído por varias dificultades que observó
en la descripción de algunos fenómenos fundamentales. Es muy conocido el hecho
de que en 1895 (a los 16 años de edad), siendo estudiante en la pequeña ciudad
suiza de Aarau, comprendió que la mecánica de Newton y la teoría de Maxwell
eran incompatibles. El argumento es por demás simple, pero no trivial: si suponemos
un observador que corre al lado de un rayo luminoso con la velocidad de la luz,
lo que deberá percibir son sólo las vibraciones del campo electromagnético,
pues respecto del corredor nada se propaga; sin embargo, ni en la óptica ni
en la teoría electromagnética existe luz que no se propague. Luego, aunque la
mecánica autoriza a pensar en los términos anteriores, no existe tal luz en
reposo y algo deja de funcionar al combinar mecánica y electromagnetismo. Otros
ejemplos de que la teoría era aún insatisfactoria, los veía Einstein en la asimetría
de la descripción cuando se consideraba la interacción entre un imán y un conductor
en movimiento relativo,7 o
bien, en el fracaso de los intentos por detectar el movimiento terrestre respecto
del éter, que condujeron a Lorentz—pero que Einstein aún no sabía—
a su hipótesis de contracción de los cuerpos en movimiento.
Einstein partió del argumento de que ni los fenómenos mecánicos ni los electromagnéticos poseen propiedad alguna que corresponda a la noción de reposo absoluto; esta observación le sugirió que "las mismas leyes de la electrodinámica y la óptica son válidas para todos los sistemas de referencia para los que son válidas las leyes de la mecánica", conjetura que después elevó al nivel de postulado con el nombre de principio de la relatividad. Al anterior agregó un segundo postulado que verdaderamente separa a la nueva teoría de la clásica, en el que establece que "la luz viaja en el vacío con la misma velocidad c, independientemente del estado de movimiento de la fuente emisora"; con ello Einstein logró tener en las manos todas las herramientas con que construyó la relatividad especial y recuperó la consistencia entre la mecánica y el electromagnetismo (a expensas, de modificar apropiadamente a la primera). El primer paso que dio lo llevó a concebir la transformación de Lorentz (como la llamó Poincaré) como un efecto cinemático, característico de la estructura del espacio-tiempo que surge de sus postulados. Conviene aquí observar la profunda diferencia que existe entre esta descripción y la de Lorentz, quien en su momento interpretó la contracción por él descubierta, como se ha dicho, como debida al cambio en las fuerzas entre el éter y los iones, generado por el cambio de la velocidad (respecto del éter). Para Einstein se trataba de un efecto universal puramente cinemático y recíproco (independiente de las teorías específicas): si dos observadores se mueven relativamente, cada uno verá las longitudes del otro contraídas, con la misma ley, al medirlas desde su propio sistema de referencia.
La nueva descripción le permitió a Einstein construir la electrodinámica de los cuerpos en movimiento —éste es precisamente el título de su famoso trabajo— a partir de la electro-dinámica de Maxwell para cuerpos en reposo. No aparece en la teoría la necesidad de introducir un éter, pues en ningún momento se requiere echar mano de nociones como espacio absolutamente estacionario o velocidad en el espacio vacío en el que tienen lugar procesos electrodinámicos, por lo que Einstein propuso dejar de lado la noción de éter, por superflua. El campo electromagnético se ha transformado con esto en un estado del espacio y ha adquirido un status ontológico a la par con la materia: el mundo físico está hecho de materia y campos; ambos entes son portadores de atributos físicos sustanciales como energía, momento, etcétera.
Para la relatividad especial la noción de éter es innecesaria; sin embargo,
no demanda que se niegue al éter; de hecho, en un trabajo de revisión de 1907,
Einstein insistió en que era el éter, entendido como asiento de las fuerzas
eléctricas y magnéticas, el que no cabía en la teoría, pues "los campos electromagnéticos
aparecen no como estados de una suerte de materia, sino como entes que tienen
existencia independiente, de naturaleza similar a la de la materia ponderable
y que tienen la propiedad de inercia en común con ella".8
¿Y el campo gravitatorio? En la teoría general de la relatividad que Einstein construyó en el curso de la década 1907-1916, la estructura (la métrica) del espacio-tiempo quedaba determinada por la materia, a través de su campo gravitacional que aparecía así como un elemento irreducible (ineliminable) de la descripción; además, la inercia (masa) del campo gravitatorio, era a su vez fuente de efectos gravitacionales lo que hace que esta teoría no sea lineal. Esto contrasta con el campo electromagnético, que puede ser nulo en las teorías clásicas y no interacciona directamente consigo mismo por no poseer cargas. La dualidad irreducible materia-campo gravitatorio —a la que cabría agregar el campo electromagnético que es lógicamente independiente y no es parte estructural indispensable del espacio-tiempo— es poco atractiva o verosímil conceptualmente. Por ello, desde el inicio de esta teoría, Einstein se dio a la tarea —nunca concluida— de elaborar una teoría unificada, en la que se eliminaría tal dualidad vía el descubrimiento de un solo ente ontológico, del que se derivarían todos los demás.
Para la teoría general de la relatividad queda abierta la posibilidad de que no exista cosa tal como "el espacio vacío", libre de toda forma de materia o campos. Y puesto que el campo gravitatorio es irreducible, llena todo el espacio y lo dota de atributos físicos, bien se le puede considerar como el éter de la teoría general de la relatividad. Este punto de vista fue adoptado por Einstein, cuando escribió (1920), por ejemplo, que: "De acuerdo con la teoría general de la relatividad, el espacio sin éter es inimaginable; en tal espacio... no tendrían posibilidad de existir varillas de medición y relojes ni tampoco intervalos espacio-temporales en el sentido de la física..." Espacio-tiempo, campo gravitatorio y éter se han transformado aquí en una noción única.
CAMPOS Y VACÍO EN LA FÍSICA CUÁNTICA
Con el advenimiento de la física cuántica, el panorama cambió drásticamente,
tanto para los campos como para el éter. De hecho, el término mismo de éter
se convirtió en obsoleto —quizá por gastado— y tuvo que cederle su
lugar al de vacío. Pero este vacío está muy lejos de ser la nada; es,
por lo contrario, un agitado océano de energía, tan rico que no sería una grave
exageración decir que la física contemporánea es, en mucho, la física del vacío.9
El vacío cuántico está —o mejor, como veremos, los vacíos cuánticos están—
en constante interacción con la materia ordinaria y determina a través de ello
muchas de sus propiedades; es extraordinariamente complejo —muy distante
conceptualmente de los modelos mecánicos newtonianos y del reposo— y quizá
una yuxtaposición de varios sistemas, cada uno de los cuales puede tener incluso
varios estados. Este vacío posee otra característica que lo diferencia esencialmente
de sus ancestros precuánticos: a pesar de cualquier cosa que se le hiciera al
viejo vacío, seguía siendo vacío; el nuevo, no. Por ejemplo, al darle suficiente
energía en condiciones apropiadas, puede llegar a responder dando a cambio partículas
y antipartículas.
En términos simples, la situación es la siguiente. Sabemos que la materia común sigue en realidad leyes cuánticas, lo que significa, entre otras muchas cosas, que aun libre, un electrón, digamos, tiene un comportamiento muy complejo y azaroso, aunque desde una perspectiva estadística se comporte con mucha regularidad; estadísticamente hablando, por ejemplo, cumple con precisión la ley de conservación de la energía; sin embargo, su energía instantánea podría diferir arbitrariamente de la que se seguiría de esta ley. Sucede que también los campos obedecen leyes cuánticas y con ellos ocurren cosas similares. Por ejemplo, es un hecho histórico que la primera ley cuántica la descubrió Max Planck (1858-1947) precisamente como una propiedad del campo electromagnético. Además; como en la teoría cuántica el comportamiento de un electrón está descrito por una función que tiene propiedades campales —es en efecto un campo electrónico— también ésta debe ser cuantizada a su vez, dando por resultado que, por ser cuánticos, ñlos electrones deben recuantizarse! (esto se conoce como segunda cuantización).
En todos los casos la cuantización otorga propiedades discretas al sistema, similares a las de sistemas compuestos por corpúsculos más o menos independientes, por lo que el lenguaje y la imagen más usados para referirse a estos efectos es el corpuscular. A estas estructuras se les llama cuantos (o quanta, si se prefiere el latinismo) del correspondiente campo. Por ejemplo, los cuantos del campo electromagnético son los fotones; los cuantos del campo de electrones-positrones pueden ser electrones o positrones, etc. Todos los sistemas cuánticos poseen un estado de mínima energía, a partir del cual pueden ir pasando a los diferentes estados físicamente posibles por acrecentamiento (continuo o discreto, según el caso) de su energía. El estado de mínima energía de un campo corresponde a la ausencia de sus corpúsculos (cero fotones, o cero electrones, etc.) y representa precisamente al vacío del campo en cuestión.
Por el hecho de que un campo cuántico se encuentre en su estado de mínima energía, sus propiedades no dejan de ser las características de los sistemas cuánticos; en particular, mantiene la propiedad de ser fluctuante, lo que significa que no desaparece. El campo de vacío está entonces en condiciones de interactuar con la materia y de imprimir sus huellas y reflejar su presencia a través del comportamiento de ésta. Si agregamos a esto la rica multiplicidad de vacíos característicos de la teoría cuántica, fácilmente podemos percibir la enorme riqueza y complejidad del mundo físico que suscita este cuadro. Como puede apreciarse, el tema es realmente importante, pero no lo desarrollaremos aquí más allá de algunos comentarios adicionales.
Un primer comentario se refiere al vacío del campo electromagnético. No es difícil convencerse de que se puede llegar a la idea de la posible existencia del vacío del campo de radiación de Maxwell por la vía clásica, es decir, sin recurrir a la teoría cuántica. Se sabe que las cargas aceleradas emiten radiación electromagnética —precisamente así generó Hertz las primeras ondas electromagnéticas intencionalmente producidas por el hombre, y así se siguen generando—. Pensemos pues en cada electrón en el Universo como una minúscula antena, todos ellos estarán emitiendo y crearán colectivamente un campo electromagnético en cada punto del Universo, terriblemente complejo y violentamente fluctuante. En condiciones de evolución como las alcanzadas por el Universo, parece razonable suponer que este campo de fondo (llamado de punto cero) resulta estadísticamente estable y, por su carácter fluctuante e ineliminable, es el que se debe identificar con el vacío electromagnético. Aún se ha de completar el argumento, pues se debe tomar en cuenta que ahora cada electrón está inmerso en el campo de vacío que hay en su localidad, por lo que al interaccionar y absorber energía de él, adquiere un movimiento aleatorio muy complejo. Si resulta posible que para cada electrón la tasa media de emisión de energía sea igual a la de absorción, cada átomo se encontrará en equilibrio. Sin embargo, ahora el átomo resulta ser un sistema abierto con propiedades novedosas, en el que se dan permanentemente fenómenos aleatorios. Estas ideas han sido exploradas con cierto detenimiento en los últimos años y constituyen la base de una teoría denominada electrodinámica estocástica. Ha sido posible demostrar que muchas de las propiedades cuánticas de los átomos —y hay razones para pensar que podrían ser todas— son originadas por este mecanismo.
Para mostrar con un ejemplo simple algo de la física de estos sistemas, vamos
a revisar el siguiente problema. Pensemos en un electrón que se mueve en el
espacio libre de fuerzas y campos externos; la única acción que sentirá en este
caso provendrá de su interacción con el vacío; consideremos a la del campo de
radiación de punto cero como la más importante (lo que sería el caso normal).
El electrón en movimiento respecto de este campo sentirá en general una fuerza
de fricción proporcional a su velocidad, que tenderá a frenarlo.10
Pero,
por otro lado, se sabe que este electrón debe mantener su velocidad, pues de
otro modo se estaría violando el principio de inercia. ¿Cómo podemos hacer compatibles
ambos puntos de vista? Un cálculo (no elemental, pero tampoco complicado) permite
mostrar que la fuerza sobre el electrón (no relativista) debida al campo es
de la forma
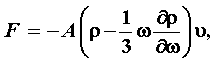
donde A es una constante que caracteriza el sistema en interacción con el campo, v su velocidad y j(w) es la densidad espectral de la energía del campo. El problema se resuelve si esta fuerza de fricción se anula, lo que ocurre si la densidad espectral del campo cumple con la condición j - 13 wddw j = 0.
La solución de esta ecuación diferencial es j=Cw3, lo que quiere decir que un vacío electromagnético con densidad espectral proporcional al cubo de la frecuencia garantiza el movimiento inercial de una carga a través de él. Como es previsible, éste es exactamente el espectro que tiene el campo de vacío, tanto en la electrodinámica cuántica como en la electrodinámica estocástica.
Bien, el electrón puede mantener su velocidad constante en el vacío; pero, ¿qué pasa si se mueve aceleradamente? La respuesta es muy interesante y constituye un tema al que se ha dedicado un esfuerzo considerable en los años recientes. Sucede que la densidad espectral del campo que el electrón ve cuando se mueve aceleradamente, deja de tener la forma simple anterior que corresponde al vacío —es decir, a temperatura nula— y toma la de una distribución de Planck a una "temperatura equivalente" determinada por la aceleración: parecería que el vacío efectivo del electrón acelerado se ha "calentado" y ha perdido su isotropía. Recordemos incidentalmente que en el espacio interestelar la radiación de fondo no es de temperatura nula, sino cercana a 3ñ Kelvin. Respecto de este campo de fondo que representa nuestro sistema natural de referencia, sí es posible determinar el movimiento de la Tierra. En el apéndice a este trabajo —que es de carácter más avanzado por las matemáticas empleadas ahí, pero cuya lectura no es indispensable— se muestra con un ejemplo adicional relativamente sencillo la complejidad que puede alcanzar el vacío al interaccionar con la materia.
En este apéndice se muestra a vuelo de pájaro un fenómeno muy general e importante
al que ya hemos hecho referencía: el hecho de que las interacciones modifican
(en ocasiones, incluso determinan) las propiedades de las partículas.11
Vamos
a ver, en particular, cómo dentro de las teorías contemporáneas llamadas de
norma (tema que desarrolla Matías Moreno en su exposición), la masa de
ciertas partículas surge como consecuencia de sus interacciones. Sin embargo,
el lector debe tener presente que el material aquí presentado tiene un carácter
matemático mucho más avanzado que el resto del texto y que su lectura es optativa.
Supongamos un campo clásico (es decir, no cuántico) complejo f; una teoría típica de este campo se construye a partir de un lagrangiano como el siguiente:
El término t =(dmf)( dmf*) (que es no negativo) representa la versión relativista de la energía cinética, mientras que
es un potencial. Normalmente m representa la masa del campo f, por lo que m2 es real y positiva; sin embargo, podemos ser más generales y aceptar a m como un parámetro, lo que significa que debemos considerar valores positivos y negativos para m2. El término l 2 = l(ff*)2 describe una interacción del campo f consigo mismo, es decir, es un término que genera una fuente para el campo f, la cual depende del propio campo f (éste es un típico ejemplo de una teoría no lineal, con autointeracciones). Una característica muy importante de esta teoría es que L(y t y v por separado también) es invariante frente a la transformación local de norma (q es una constante)
Considerado el potencial v como una función de p, posee mínimos sólo si l>0, que es el único caso que estudiaremos; entonces, si m2>0, v posee un mínimo para j = 0, es decir, para f>=0, lo que corresponde al estado base o vacío de este sistema, el que obviamente es invariante frente a la transformación de norma (1). Todo resulta normal, pero no se obtiene nada especialmente interesante. Consideremos, sin embargo, el caso m2<0, por lo que m no es más una masa. En este caso, j=0 corresponde a un máximo, como puede apreciarse en la figura, y el mínimo está fuera del origen y ocurre para
De este resultado se sigue que el campo complejo f que corresponde al estado de vacío tiene la forma
con z, una fase arbitraria. Hemos obtenido así no
uno, sino un continuo de estados de vacío para este sistema (vacío degenerado);
como la solución en el origen es inestable, éstos son los verdaderos vacíos
del campo, cada uno de los cuales ha dejado de ser invariante frente a la transformación
(1) de invariancia del lagrangiano. En otras palabras, el estado de vacío de
este campo posee menos simetrías que el lagrangiano del cual se deriva y es
degenerado; o bien, el estado de menor energía no es el más simétrico. Cuando
esto sucede, se acostumbra decir que ha ocurrido una ruptura espontánea de la
simetría."12
![[FNT 12]](../img/136_89.gif)
Los diferentes estados del campo f los podemos escribir ahora en la siguiente forma, separando sus partes real z e imaginaria X (esto equivale a tomar como vacío el que se encuentra sobre el eje real):
donde los nuevos campos z y X son reales y nulos en el estado base. Con esta escritura, el lagrangiano resulta (omitiendo términos constantes que son dinámicamente irrelevantes):
Esta expresión puede parecer muy complicada y casi incomprensible. Pero si comparamos con el lagrangiano original vemos que ella corresponde a un campo real x sin masa, más un campo z con masa:
los cuales interaccionan entre ellos y entre sí mismos. La teoría ha generado en esta forma, a partir de un campo f complejo sin masa, dos campos reales, uno sin masa y otro con masa, cuya ley de interacción queda determinada por la propia teoría. Nótese de manera particular que la masa mz está determinada por la constante de autoacoplamiento del campo inicial l, y por el valor del vacío a través de R.
Boyer, T. H. "The Vacuum in Classical Physics". Scientific American, 253 (2), 70 (agosto de 1985).
Braun, E. Una faceta desconocida de Einstein. Fondo de Cultura Económica-SEP, México, 1989, Colección La Ciencia desde México.
Cetto, A. M. La luz. Fondo de Cultura Económica-SEP, México, 1989. Colección La Ciencia desde México.
De la Peña, L. Albert Einstein, navegante solitario. Fondo de Cultura
Económica-SEP, México, 1989, colección La Ciencia desde México.
De la Peña, L. y A. M. Cetto, "Teorías estocásticas de la mecánica cuántica". Rev. Mex. Fis. 37 (1991), 17.
Dodd, J. E. The Ideas of Particles Physics. Cambridge University Press, Cambridge, 1984.
Einstein, A. Investigations on the Theory of the Brownian Movement. Editado y anotado por R. Fñrth, Dover, 1956.
Einstein, A. (1949) "Autobiographical Notes". En P. A. Schilpp. Albert Einstein: Philosopher-Scientist, Open, Court, 1970.
Faraday, M. (1831) Experimental Researches in Electricity. Dover, 1965.
Lorentz, H. A., A. Einstein, H. Minkowski, y H. Weyl, 1923, The Principle of Relativity (anotado por A. Sommerfeld). Dover.
Maxwell, J. C. (1891) A Treatise on Electricity and Magnetism. Dover, 1954.
Nersessian, Nancy J. Faraday to Einstein: Constructing Meaning in Scientific Theories. Martinus Nijhoff Publishers, Dordrecht, Países Bajos, 1984. El autor ha descansado in extenso en esta obra durante la elaboración de las notas.
Podolny, R. Something Called Nothing. Mir Publishers, Moscú, 1986.
![[Inicio]](../img/begin.gif)
![[Anterior]](../img/prevsec.gif)
![[Siguiente]](../img/nextsec.gif)