I. LOS MITOS DEL CAOS

LA METAF�SICA ocupa un lugar importante dentro del conocimiento humano, ya que el hombre al preguntarse acerca del origen del mundo, lo hace tambi�n del suyo propio. Es tan sencillo como decir que la metaf�sica empieza donde termina el lenguaje de la ciencia. A pesar de que los griegos tuvieron filosof�a y los jud�os s�lo religi�n, es interesante hacer notar que el pensamiento metaf�sico fue m�s acentuado en los griegos. A diferencia de los mitos babil�nicos y griegos, en los cuales el mundo tiene su origen en peleas entre los dioses paganos, en el Antiguo Testamento se hace un planteamiento racional, no antropom�rfico e incluso casi cient�fico del origen del mundo. Si nos referimos al texto del Antiguo Testamento vemos que la primera de las especificaciones teol�gicas es el enunciado del estado ca�tico original de la Tierra, el cual se plantea con la ayuda de una serie de conceptos corrientes en el pensamiento cosmol�gico sacerdotal. Tohuwabowu significa lo informe, la masa primigenia de aguas rodeada de tinieblas, designa al caos en su aspecto material como un elemento primordial l�quido, pero suscita al mismo tiempo una asociaci�n con el aspecto dimensional: tehom = oc�ano ca�tico es el abismo c�smico (la palabra est� relacionada ling��sticamente con Tiamat, el drag�n babil�nico del caos, cuya destrucci�n a manos de Marduk permite la creaci�n del Universo). Edmundo Valad�s (El libro de la imaginaci�n) nos narra la siguiente versi�n de la creaci�n proveniente de la teogon�a n�huatl.

El mundo estaba lleno de agua. Y en el agua viv�a la Se�ora de la Tierra. Era un monstruo cubierto de ojos y de fauces. Tezcatlipoca y Quetzalc�atl decidieron darle forma a la Tierra. Convertidos en serpientes, enlazaron y estrecharon al monstruo hasta que se rompi� en sus dos mitades. Con la parte inferior hicieron la Tierra y con la parte superior el cielo. Los otros dioses bajaron a consolarla y, para compensar el da�o que Tezcatlipoca y Quetzalc�atl acababan de hacerle, le otorgaron el don de que su carne proporcionara cuanto el hombre necesita para vivir en el mundo.

Tras todo lo creado subsiste el abismo de lo informe, que puede ser continuamente engullido por ese abismo; el caos constituye, en suma, una perpetua amenaza para las criaturas. Cuando hablamos de caos, la primera idea que nos viene a la mente es de car�cter negativo, como una imperfecci�n, algo que causa inquietud y, m�s a�n, se ve como una forma del Mal. El tema, como dice Pierre Tuiller, fil�sofo e historiador de la ciencia, ha sido uno de los m�s discutidos, y en todas las mitolog�as, religiones y filosofas se ha tratado de resolver la pregunta clave: �cu�l es el orden universal?

EL CAOS DETERMINISTA

En a�os recientes, parte de la comunidad cient�fica en todo el mundo ha comenzado a hablar incesantemente de caos, desorden, aperiodicidad, para explicar muchos fen�menos que se suceden en la naturaleza y en experimentos controlados de laboratorio, que se caracterizan por tener un comportamiento que no puede ser descrito por leyes matem�ticas sencillas. M�s extra�o a�n es el hecho de que este tipo de caos emerge de fen�menos cuya evoluci�n es inicialmente determinista. Contrariamente a lo que podr�a esperarse, al aumentar la cantidad de informaci�n disponible no se evita la imposibilidad de conocer la progresi�n futura del sistema. Dicha evoluci�n queda determinada por su pasado y una de las propiedades peculiares del caos es que la m�nima incertidumbre en la definici�n de las condiciones iniciales se amplifica exponencialmente, alcanzando proporciones macrosc�picas que impiden conocer lo que suceder� a largo plazo.

El descubrimiento del caos determinista ha forzado un cambio sustancial en la filosof�a de la ciencia: por una parte, establece l�mites a nuestra capacidad para predecir un comportamiento; por otra, abre un nuevo espacio para comprender muchos fen�menos aleatorios que suceden en varios campos del conocimiento. Sin embargo, la aceptaci�n que estos fen�menos han tenido entre los cient�ficos no ha sido general, el polvo de la casa a veces se suele esconder c�modamente debajo de la alfombra, pero tarde o temprano requerir� de nuestra atenci�n. El polvo afea el orden, pues si existe un componente de aleatoriedad o de imperfecci�n se destruyen las simetr�as intr�nsecas que simplifican la predicci�n f�sica. Sin embargo, a pesar de que se niegue su existencia las evidencias son contundentes: el polvo se manifiesta en la f�sica a escalas tan microsc�picas como es la distribuci�n de los niveles de energ�a en ciertos sistemas at�micos; en qu�mica se describen reacciones oscilatorias en las que, una vez desencadenadas, al cabo de cierto tiempo parece regresarse a los reactivos de partida. En los movimientos de los planetas de nuestro Sistema Solar tambi�n encontramos comportamientos desordenados, as� como en los cambios clim�ticos, el ritmo cardiaco, la vida econ�mica y las epidemias que atacan a la humanidad, por nombrar s�lo algunos. Definir el concepto de desorden no es una tarea f�cil ya que cada quien tiene una idea propia de �l. En ciertos casos evoca un estado de confusi�n, una disposici�n de cosas m�s o menos irregular, pero independientemente de los giros sem�nticos la idea general es que el orden ha sido gravemente perturbado. El desorden se presenta entonces como algo que nunca debi� haber existido y en el dominio de las ciencias se le acusa de delincuente que viola las "leyes de la naturaleza". Durante mucho tiempo, la ciencia ha hecho suyo el credo de que detr�s de los des�rdenes aparentes de la naturaleza siempre existe un orden escondido. Predecesores de esta filosof�a son los pitag�ricos y Plat�n. Para este �ltimo el estado ideal del Cosmos es cuando cada cosa est� en su lugar. La racionalidad del Cosmos la interpreta como el resultado de una operaci�n efectuada por un poder ordenador, una figura semim�tica a la que llama Demiurgo, especie de "obrero" que ordena el desorden al crear el Cosmos, palabra que significa en primer lugar belleza, arreglo, orden y en segunda instancia, mundo, es decir, orden del mundo. Nos dice Plat�n:

con todo aquello en desorden, el dios insert� proporciones en cada cosa respecto de s� y respecto de los dem�s, esas simetr�as eran tan abundantes como fue posible y se encontraban en las cosas ajustadas seg�n proporci�n y medida com�n [...] todas esas partes primero fueron ordenadas y luego se constituy� con ellas ese todo, viviente �nico que contiene en s� mismo a todos los vivientes mortales e inmortales.

El mundo es matem�ticamente ordenado y el trabajo del hombre de ciencia consiste en encontrar las estructuras racionales que sirvieron de modelo al Demiurgo. Seg�n Plat�n, en el campo de los elementos microsc�picos estas formas perfectas se identifican con los poliedros regulares, en particular con el c�rculo. Por ello los astr�nomos, hasta Kepler, redujeron todas las trayectorias celestes a c�rculos o combinaciones de ellos. Sin embargo el mismo Plat�n, aunque obsesionado por el orden, le presta gran atenci�n a los des�rdenes y sugiere que el orden ideal no puede ser jam�s instaurado de manera absoluta en los objetos materiales. Hay algo que se resiste, que impide a las estructuras matem�ticas realizarse perfectamente: la Naturaleza emergida de las manos del Demiurgo es sede de una agitaci�n permanente.

Podemos, por tanto, afirmar que la ciencia ha estado influida durante muchos siglos por los conceptos de Plat�n, quien delinea tres niveles principales de jerarquizaci�n. En el nivel superior se encuentran las ideas y formas matem�ticas que constituyen los modelos ideales de todas las cosas. Es el dominio del ORDEN. Al otro extremo se encuentra el CAOS, estado primordial carente de orden y desorden, que escapa a toda descripci�n.

Entre esos dos niveles est� nuestro mundo, resultado del trabajo del Demiurgo, que tiene un poco de orden y desorden. Aunque idealmente es ordenado y obedece a leyes deterministas, no est� exento de car�cter aleatorio. Uno de los postulados que ha regido la ciencia nos dice que existen regularidades en la sucesi�n temporal de los eventos que ocurren en el universo material y en algunas caracter�sticas mensurables de los sistemas materiales relativamente aislados, cuando est�n en equilibrio. Como afirma A. Rosenblueth, este principio es la esencia del determinismo o la causalidad, puesto que implica que es posible predecir el futuro de un sistema si se conocen en un momento dado las condiciones de los elementos que lo constituyen. Las ecuaciones que empleaba la f�sica cl�sica para expresar sus leyes, tanto las que se refer�an a los equilibrios como las que expresaban los procesos din�micos, ten�an una forma que implicaba relaciones causales precisas y rigurosa entre sus variables; eran, por lo tanto, compatibles con las formulaciones filos�ficas del principio de causalidad.

EL COLAPSO DE LA PREDICCI�N

Una de las primeras sacudidas a la s�lida estructura del determinismo la proporcion� la conocida teor�a cin�tica de los gases, desarrollada por J. G. Maxwell y luego perfeccionada por L. Boltzman. En ella se trata de concebir y analizar los mecanismos ocultos presentes en un gas, y con ello explicar las propiedades manifiestas en el nivel macrosc�pico (volumen, temperatura, presi�n). Supusieron que las sustancias estaban compuestas de �tomos, pero en lugar de razonar en forma individual, manejaron el problema en forma estad�stica y calcularon promedios bas�ndose en el principio de que la energ�a del gas se distribuye uniformemente entre las part�culas que lo componen (principio de equipartici�n de la energ�a). Maxwell y Boltzman, como nos dice P. Tuiller, hacen emerger el orden del caos, pues las regularidades observadas en el nivel macrosc�pico provienen de la incapacidad que tenemos para predecir las trayectorias individuales de los �tomos.

El lenguaje de la estad�stica es una manera subjetiva de analizar la objetividad de la naturaleza. Recurrimos a ella no porque los acontecimientos sean de naturaleza azarosa, sino porque desconocemos subjetivamente cu�l va a ser el curso que van a tomar dichos acontecimientos. Cada una de las partes que integran los sistemas de la naturaleza tiene una historia individual, pero como integran sistemas tan complejos, en los cuales interviene un n�mero tan grande de partes, es imposible conocer la historia individual de cada parte y por ello debemos recurrir a la estad�stica.

La estructura determinista termina de colapsarse con la aparici�n de la teor�a de la mec�nica cu�ntica, en particular con el principio de incertidumbre de Heisenberg, el cual postula que no se puede medir al mismo tiempo la posici�n y la velocidad de una part�cula. Si se requiere precisar d�nde est� la part�cula, su momento lineal se vuelve indefinido y viceversa: al tratar de definir la velocidad dentro de l�mites estrechos, menos se sabe d�nde se halla la part�cula. De lo anterior se deduce que de acuerdo con la mec�nica cu�ntica, cualquier medida inicial es siempre insegura y que el caos asegura que las incertidumbres sobrepasan la habilidad de hacer cualquier predicci�n. No es de extra�ar que la teor�a cu�ntica tuviese numerosos opositores cuando fue elaborada. De acuerdo con el principio de incertidumbre de Heisenberg, el macroorden de la naturaleza depender�a del microcaos de los procesos �ntimos de la materia. En el campo de las ciencias naturales, el embate contra el determinismo fue similar. Un ejemplo lo constituyen las teor�as sobre la gen�tica desarrolladas por Gregor Mendel, formuladas en 1865, pero que fueron aceptadas a partir de 1900. Antes de los trabajos de Mendel se admit�a como cierto el dogma de la g�nesis, seg�n la cual las especies fueron creadas en pares �nicos, hembra y macho, en un punto de la Tierra a partir del cual se propagaron. Una especie que ten�a caracter�sticas intermedias entre dos de ellas era considerada un h�brido, un mutante, algo que romp�a el orden y deb�a desaparecer para regenerar el modelo deseado por el Creador. Las leyes de Mendel sobre la hibridaci�n aportaron a la biolog�a un concepto revolucionario para su �poca, el cual indica que los organismos no se reproducen a s� mismos y por tanto no transmiten sus propios caracteres, sino que procrean aportando a sus descendientes s�lo la mitad de su patrimonio gen�tico. Cont� los granos y aplic� los m�todos preestad�sticos de su �poca, bas�ndose en la ley de grandes n�meros, pero sin conocer a fondo la teor�a matem�tica. De su trabajo se deduce que las mezclas de especies siempre son posibles y que resultan tan fecundas como sus progenitores, mientras que los h�bridos, cuando llegan a ser viables son frecuentemente est�riles. No obstante, el grado de esterilidad no se encuentra asociado estrictamente con la afinidad de las formas, pues est� gobernado por leyes complicadas y todav�a escasamente conocidas.

Tal vez el m�s destacado de los cient�ficos de las ciencias naturales haya sido Charles Darwin, quien dec�a simplemente que las variaciones aleatorias, seleccionadas en forma ciega, pueden engendrar toda la diversidad de formas vivientes. He aqu� otro buen ejemplo del desorden que engendra el orden.

En resumen podemos decir que existe una ciencia del desorden, de la cual describiremos algunos ejemplos en el curso de esta obra, pero a diferencia de la ciencia plat�nica, su existencia misma no hace desaparecer los des�rdenes que ella estudia. En cierta escala, todos los fen�menos son desordenados, irregulares y no pueden reducirse a formas puras. La ciencia del caos encuentra el desorden escondido entre un aparente orden real.

BORGES Y EL DESORDEN

Prosigamos esa historia del caos con un cuento... de Jorge Luis Borges. En "La loter�a de Babilonia" el personaje central relata que este juego formaba parte principal de la realidad, y si bien poca gente lo jugaba, una organizaci�n, llamada La Compa��a, despert� el inter�s del p�blico al incorporar unos cuantos resultados negativos dentro de los n�meros favorables. La loter�a era secreta, gratuita y general. Todos participaban en los sorteos y las consecuencias eran incalculables, pues el asesinato de alguien o el descubrimiento de un tesoro pod�a ser el resultado de numerosos sorteos previos. Si la loter�a era una peri�dica infusi�n del caos en el Cosmos, mejor ser�a que el azar interviniese en todas las etapas del sorteo y no en uno solo. Ninguna decisi�n es final y todas se ramifican en otras. Cuenta el personaje que hay quien dice que La Compa��a no existe y que el desorden de nuestras vidas es puramente hereditario, mientras que otros declaran que es omnipotente, pero s�lo influye en cosas min�sculas (como por ejemplo, el aleteo de una mariposa). �Se suceden los hechos al azar o funciona el mundo siguiendo reglas que podemos descubrir? Si decimos que el mundo tiene un sentido, y si �ste es perfectamente inteligible, esto significa que el pasado y el futuro est�n abiertos ante nosotros como un libro. Por el contrario, si negamos lo anterior, no es posible discernir ninguna regla y si no entendemos el pasado, menos podremos predecir el futuro. La verdad, parece ser, se encuentra a medio camino entre esas dos aseveraciones, pero antes de abogar por ella, presentemos las dos versiones.

EL AZAR

El azar, seg�n una definici�n cl�sica, es la intersecci�n de series causales independientes. Lo aleatorio, en oposici�n al determinismo, es la independencia del pasado y del futuro. Un personaje del cuento de Borges sale de su casa y despu�s de caminar un tiempo le cae un objeto encima que lo mata: �fue el azar? Hay quien afirma que no existen las series causales independientes en nuestro Universo: al caminar, el personaje ejerce en la calle una fuerza de atracci�n sobre el objeto que lo va a matar, ya que la cantidad de viento que desplaza en su movimiento es inseparable de todo un contexto meteorol�gico en el que la actividad pasada de la v�ctima ha tenido su contribuci�n. A veces uno oye decir que los movimientos de los planetas obedecen leyes rigurosas, mientras que la tirada de un dado es fortuita o sujeta al azar. Karl Popper dec�a que la diferencia entre estas dos cosas reside en el hecho de que no somos capaces de predecir los resultados individuales de las tiradas de un dado. Para deducir predicciones se necesitan leyes y condiciones iniciales: si no se dispone de leyes apropiadas o si no se pueden averiguar las condiciones iniciales, el modo cient�fico de predecir se desmorona. Sin duda alguna, cuando tiramos un dado no tenemos el conocimiento suficiente de las condiciones iniciales; si dispusi�ramos de mediciones suficientemente precisas tambi�n ser�a posible hacer predicciones en este caso, pero las reglas para tirar el dado correctamente est�n elegidas de tal modo que nos impiden medir las condiciones iniciales, por lo tanto decimos que el proceso es aleatorio.

EL DETERMINISMO

Por otra parte, A. Rosenblueth en su libro Mente y cerebro nos describe con acierto uno de los postulados cient�ficos que se han adoptado en la ciencia, del cual ya hablamos con anterioridad. Seg�n �ste, existen regularidades en la sucesi�n temporal de los fen�menos que ocurren en el universo material y hay caracter�sticas que son mesurables en los sistemas materiales relativamente aislados cuando est�n en equilibrio. �ste es el postulado del determinismo o de la causalidad, y seg�n �l, es posible predecir los estados futuros de un sistema material si se conocen en un momento dado las condiciones de los elementos que lo constituyen. Todo lo que se producir� ma�ana tiene una causa hoy, y un conocimiento bastante preciso de la causa permitir� predecir el efecto. Dos tipos de situaciones se presentan en los sistemas materiales: en el primero el tiempo es una de las variables, mientras que en el segundo no existe tal variable. En cualquiera de los dos casos la herramienta cl�sica que se emplea para describirlos es la ecuaci�n diferencial. Si un fen�meno est� regido por ella, su evoluci�n est� totalmente inscrita en su estado presente: el conocimiento perfecto de �ste permite reconstruir su pasado y predecir su futuro. La ecuaci�n diferencial es una relaci�n v�lida en cada instante entre la posici�n de un m�vil, su aceleraci�n y su velocidad. Cuando se integra la ecuaci�n se deduce la trayectoria del m�vil y su desplazamiento sobre �sta. Una relaci�n instant�nea entre la posici�n y la velocidad permite determinar por completo tanto una como otra, siempre y cuando se conozca la posici�n en el instante inicial. Eli de Gortari (Ensayos filos�ficos sobre la ciencia moderna) llama la atenci�n sobre ciertas restricciones que tiene el determinismo. El presente f�sico implica siempre un lapso de cierta duraci�n y, por lo tanto, las condiciones iniciales no son estrictamente instant�neas.

Lo anterior implica que el sistema sigue evolucionando durante la condici�n inicial tomada como punto de partida, por lo cual es irrealizable la previsi�n estrictamente rigurosa del estado del sistema en un instante dado. Otro punto importante es que para conocer exactamente la posici�n en el instante inicial es necesario hacer una medici�n perfecta, cosa imposible ya que las mediciones cient�ficas est�n siempre afectadas por errores experimentales, adem�s, al medir perturbamos el sistema, pues destruimos su aislamiento.

UN DETERMINISMO DISFRAZADO DE AZAROSO

Hoy en d�a se ha llegado a la conclusi�n de que una ley puramente determinista puede manifestarse por fen�menos totalmente aleatorios. Esta caracter�stica est� dada por el car�cter no lineal de las ecuaciones matem�ticas que modelan el sistema f�sico. Dado que estas ecuaciones no permiten una soluci�n anal�tica exacta los cient�ficos han tenido dificultades para construir teor�as que permitan su predicci�n. Mucho se ha avanzado gracias al uso de las computadoras, que han permitido al matem�tico explorar e identificar pautas de comportamiento indispensables. Esta nueva aproximaci�n, en la que interviene una combinaci�n de "experimentos" num�ricos y de an�lisis matem�tico, ha dado origen a un campo llamado din�mica no lineal. Quienes trabajan en �l usan el t�rmino caos para referirse al comportamiento irregular e impredecible, aunque determinista, de los sistemas no lineales. Un primer ejemplo de un sistema no lineal, muy sencillo, que exhibe una transici�n de un comportamiento regular a uno ca�tico es el generado por la llamada ecuaci�n log�stica. Para profundizar en ella s�lo necesitamos papel, l�piz y una calculadora sencilla.

El primer paso para desarrollar la ecuaci�n consiste en definir una variable X; para aquellos que no les gusta trabajar con una simple letra, podemos sugerir que asocien la letra con una idea menos abstracta, como una poblaci�n de insectos, la cantidad de una sustancia que reacciona en un vaso o bien, si se desea, el n�mero de personas de una poblaci�n que han o�do un chiste (el lector podr� darle a X el sentido que su imaginaci�n le dicte).

As�, el sistema est� descrito por una sola variable X, es decir que para definir toda la evoluci�n del mismo, bastar� conocer el valor que toma X en cierto instante dado. Para simplificar a�n m�s las cosas diremos que la variable tiempo s�lo puede tener valores enteros. El modelo deber� entonces ser capaz de predecir el valor de X_sig a partir del �ltimo calculado, es decir, el valor de X; veamos c�mo sucede esto:

Xsig = K (l - X) X

(ecuaci�n 1)

X_sig ser� el siguiente valor calculado a partir de X; K es una constante que ser� detallada m�s, adelante.

�Empecemos! Supongamos que X vale 0.04 y K, 2.7. Calculemos el valor de X_sig:

X_sig= 2.7 (1 - 0.04) 0.04

el resultado es 0.10368. Si ahora repetimos la operaci�n, pero empleando X = 0.1, el resultado ser� 0.2430 y as� continuamos resolviendo la ecuaci�n, aumentando en cada caso el valor de X hasta llegar a 1. Una imagen, dice el refr�n, vale m�s que mil palabras, hagamos pues una gr�fica en donde en el eje horizontal dispongamos los valores de X empleados y en el vertical los que resultan de estas simples operaciones. En la figura 1 se muestra el resultado de nuestro c�lculo. Bueno, se preguntar� el lector, �qu� de extraordinario tiene dicha gr�fica? pues nada, hasta ahora; los bi�logos conocen esta ecuaci�n, descrita por P. Verhulst en el siglo pasado, que fue propuesta para modelar el crecimiento de una poblaci�n de insectos en un medio ambiente limitado. La gr�fica nos indica que cuando la densidad de poblaci�n es inicialmente peque�a, las generaciones siguientes ser�n m�s numerosas, pero s�lo hasta un l�mite, a partir del cual el crecimiento disminuye. La sobrepoblaci�n, el incremento en la mortalidad, la competencia por el alimento y muchos otros factores hacen que la poblaci�n disminuya, como se observa en la presencia de valores altos de X. Se asume que la poblaci�n no sigue un crecimiento exponencial incontrolable, como lo hab�a predicho el economista ingl�s T. Malthus en 1798, bas�ndose en una ecuaci�n del tipo:

Xsig =K X

(ecuaci�n 2)

De acuerdo con su modelo, Malthus predec�a que si no se pon�a un "freno moral" (matrimonios aplazados y continencia sexual) no tardar�a mucho para que la humanidad agotara la cantidad de alimentos disponibles. La ecuaci�n del ingl�s describe un crecimiento lineal, mientras que nuestra ecuaci�n (afortunadamente) genera un arco parab�lico que empieza a elevarse desde el origen, llega a un m�ximo y desciende sim�tricamente hasta alcanzar nuevamente el cero. La constante K hace que la altura del m�ximo se modifique, hecho que se puede demostrar si graficamos la ecuaci�n empleando un valor diferente de K.

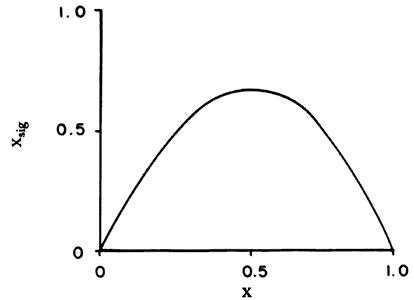
Figura 1. Forma t�pica de la relaci�n entre X y X_sig, descrita por la ecuaci�n log�stica, K = 2.7.

Hagamos una peque�a modificaci�n a nuestro c�lculo: con el mismo valor de K = 2.7, usemos inicialmente el de X = 0.04. El valor de X_sig que se obtiene se sustituye como nueva X y se obtiene otra X_sig; repitamos la operaci�n sesenta veces (en matem�ticas a esto se le llama iterar la ecuaci�n). Veamos c�mo se obtienen los dos primeros valores:

El primer resultado es 0.10368, como ya lo vimos antes; ahora calculemos con �l el siguiente:

X_sig= 2.7 (1-0.10368) 0.10368

que nos produce 0.25091. A partir de la iteraci�n n�mero dieciocho el producto es 0.6296. Si se da cualquier otro valor inicial entre cero y uno y se itera, se obtendr� el mismo valor final 0.6296. La figura 2 muestra una gr�fica de las operaciones realizadas al iterar la ecuaci�n; en el eje vertical est�n dispuestos los valores de X y en horizontal los de X_sig. Una manera sencilla de realizar las iteraciones sin necesidad de calcularlas con una m�quina, la presentamos en esta misma figura 2. Hemos trazado una recta punteada que parte del origen, cuya expresi�n equivale a X = X_sig. Supongamos que partimos del valor inicial 0.04; si trazamos una l�nea vertical hasta tocar la curva y luego una horizontal que toque la recta punteada, tendremos el valor de X_sig y de esa manera repetimos la operaci�n tal y como se describe mediante los trazos con flecha realizados en la figura. Como se puede observar, se llega a un punto fijo en el cual convergen todas las trayectorias generadas por las iteraciones.

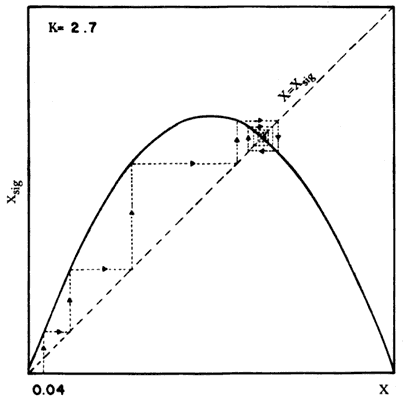
Figura 2. Iteraci�n de la ecuaci�n log�stica para K = 2.7. Presencia de un atractor.

En la figura 3 se muestra el mismo desarrollo de la ecuaci�n descrita, salvo que hemos modificado el valor de K> a 3.15. En este caso el punto fijo deja de ser estable y a pesar de que inicialmente atrae las �rbitas hacia �l, se genera una bifurcaci�n en la que aparecen dos puntos estables (marcados como X₁> y X₂ en la gr�fica) que, independientemente del valor inicial escogido, "atraen" todas las �rbitas que se generen por la iteraci�n de la ecuaci�n. Debemos aclarar que en din�mica se llama bifurcaci�n al cambio en el n�mero de soluciones posibles para una ecuaci�n cuando se var�a un elemento, en este caso, el valor de K. El asunto empieza a ponerse interesante... Hagamos otro an�lisis de la ecuaci�n empleando ahora K = 3.53. Los resultados est�n representados de una manera diferente en la figura 4; ahora en el eje horizontal est� anotado el n�mero de iteraciones de la ecuaci�n y en el vertical el valor resultante de la variable X. El periodo dos se ha bifurcado y ahora existe un ciclo de cuatro valores. En lugar de continuar describiendo el comportamiento de la ecuaci�n para diferentes valores individuales de K, presentamos en la figura 5 una vista general del modelo por medio de un diagrama de bifurcaci�n en el cual en el eje horizontal se disponen los diferentes valores de K de 3.5 hasta 4 y en el eje vertical los de X_sig normalizados de cero a uno; cada valor de la figura se ha obtenido iterando la ecuaci�n m�s de cien veces. La gr�fica de la din�mica irregular de la ecuaci�n log�stica nos da una imagen del caos. Como muchos de los sistemas no lineales que existen en la naturaleza, el modelo matem�tico exhibe un comportamiento que parece azaroso a pesar del hecho de que las ecuaciones que describen su comportamiento son enteramente deterministas. Los resultados nos ense�an que si K se sit�a entre uno y tres, pensando en el modelo de crecimiento poblacional de los insectos, los valores iniciales evolucionan a una poblaci�n que alcanza un equilibrio.

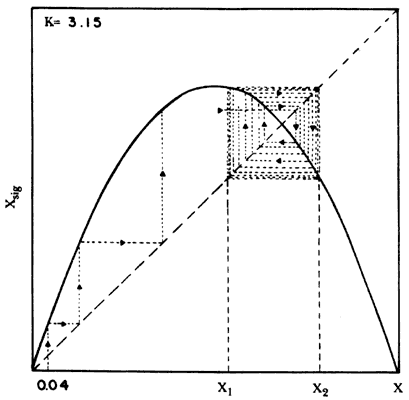
Figura 3. Iteraci�n de la ecuaci�n log�stica para K= 3.15. Presencia de dos atractores con valores X_l y X₂.

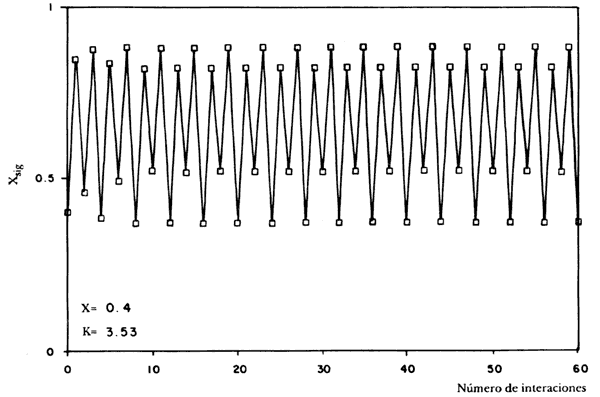
Figura 4. Valores de X para 60 iteraciones de la ecuaci�n log�stica para K = 3.53. Ciclo de cuatro valores.

LAS RUTAS DEL CAOS

Al incrementarse K entre 3 y 4 la din�mica cambia en forma notable y aparecen bifurcaciones de orden 2 que son reemplazadas por ciclos en los que se alternan cuatro valores, que luego ser�n de 8, 16, 32, 64 (como dec�a Borges, "la decisi�n final no existe, se ramifica en otras"). Este proceso, al que se le suele llamar duplicaci�n peri�dica, es una secuencia que antecede el periodo ca�tico y tambi�n se le denomina bifurcaci�n en forma de tenedor, ya que su forma recuerda tal instrumento. Este mecanismo de duplicaci�n peri�dica ha sido muy estudiado ya que representa una de las rutas hacia el caos y como veremos m�s adelante, es com�n en muchos sistemas din�micos reales. Si el lector analiza con detalle la figura 5 puede notar que las regiones de comportamiento ca�tico se ven interrumpidas por intervalos de comportamiento peri�dico, uno de ellos se presenta cuando el valor de K es 3.569, otro mucho m�s prolongado ocurre en las vecindades de K 3.83 pero aqu� se presenta un ciclo de tres valores estables al inicio del periodo, que permanece durante un corto lapso para luego desencadenar nuevamente un comportamiento ca�tico. Un esquema de este mecanismo se muestra en la figura 6. Este �ltimo proceso en el cual las bifurcaciones son impares representa otra de las rutas hacia el caos y se le conoce como intermitencia del tipo I, fen�meno que posteriormente estudiaremos en sistemas din�micos naturales.

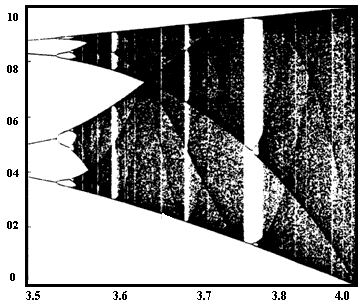
Figura 5. Diagrama de bifuraciones de la ecuaci�n log�stica cuando K var�a de 3.5 a 4. En el eje horizontal se encuentra el valor de K, en el vertical los de X.

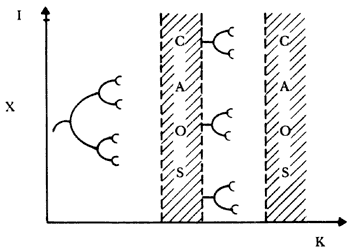
Figura 6. Detalle del diagrama de bifuraciones en la ecuaci�n log�stica para el ciclo de periodo tres.

EL CAOS

�Qu� pasa cuando el valor de K es mayor de cuatro? La situaci�n cambia en forma importante. Consid�rese la figura 7, en la cual gr�ficamente presentamos los resultados de la ecuaci�n para cinco valores de K que van desde 4.0001 a 4.0005 con un valor inicial de X= 0.4. En el eje vertical se representa el n�mero de iteraciones que llegan hasta 200 y en el horizontal el valor siguiente de X. Como se observa, cuatro de las cinco ecuaciones se salen r�pidamente de la escala negativa en las primeras 200 iteraciones, pero el orden que siguen es totalmente inesperado. La primera que se sale de la escala es la que tiene el valor de 4.0004, luego sigue la de 4.0003, y despu�s la de 4.0005. En la iteraci�n 200 s�lo la que emplea el valor de K = 4.0002 sigue en el rango entre cero y uno, hemos entrado en el r�gimen ca�tico en el cual la periodicidad es dif�cil de predecir. Volvamos un momento al ejemplo del bi�logo que sigue el crecimiento de la poblaci�n de insectos: supongamos que cada iteraci�n de la ecuaci�n representa un a�o, por tanto, s�lo uno de los sistemas representados en la figura anterior ser� estable por dos centurias, lo cual deja m�s que satisfecho a nuestro cient�fico con su predicci�n. Sin embargo, si cada iteraci�n representa una semana, el periodo de estabilidad deducido ser� mucho menor.

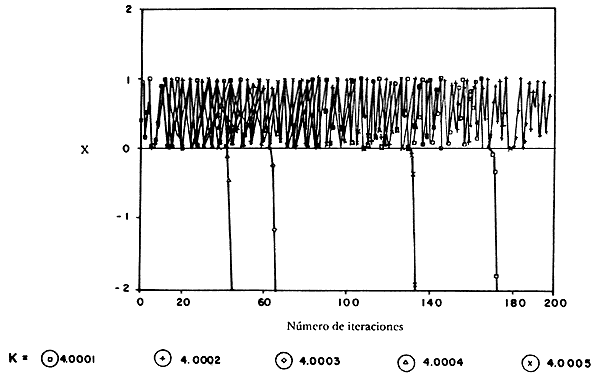
Figura 7. Iteraci�n de la ecuaci�n log�stica para cinco valores de K mayores de cuatro.

EL N�MERO 4.669 201 609 102 990 9...

Una conclusi�n interesante que resulta del estudio de la "inocente" ecuaci�n log�stica es que las bifurcaciones peri�dicas son una de las rutas hacia el caos, pero lo notable de este hecho es que dicho mecanismo es v�lido para cualquier ecuaci�n que tenga un solo valor K. La universalidad de este proceso se reproduce sin importar la f�sica detallada o la descripci�n del modelo te�rico que se estudie. M�s a�n, la din�mica de fen�menos que transitan de la estabilidad al caos por el mecanismo de la bifurcaci�n se realiza de una manera que puede evaluarse cuantitativamente, lo cual fue descubierto por M. Feigenbaum entre otros, un f�sico estadounidense que analiz� los datos de la famosa ecuaci�n con su calculadora.

Hagamos un esquema para entender lo que Feigenbaum encontr�, v�ase la figura 8. En la parte superior del diagrama hemos anotado un eje de valores para X que va de cero a uno, tal como lo hicimos con la ecuaci�n log�stica. Los s�mbolos K₁ hasta K₆ representan valores de la constante en los cuales se sucede una bifurcaci�n. Si vemos la secuencia de arriba hacia abajo se nota que cada punto es reemplazado por dos "gemelos". Seg�n el primer n�mero universal descubierto por Feigenbaum, la distancia entre los n�meros gemelos es 2.5029078750958...veces m�s peque�a que la que existe entre los puntos que les dieron origen. El lector minucioso podr� ver que cada secuencia de puntos que se origina una l�nea abajo reproduce el modelo global de la que le antecede, salvo que est�n m�s juntos. Feigenbaum encontr� adem�s que el cociente de diferencias en los valores de K requeridos para llevarse a cabo una bifurcaci�n, por ejemplo (K₃ - K₂ / K₄ - K₃), es constante y vale 4.66201... para cualquier sistema no lineal unidimensional. M�s adelante veremos que en los fen�menos f�sicos reales el paso a la din�mica ca�tica se lleva a cabo por un mecanismo similar al descrito te�ricamente por las observaciones de Feigenbaum.

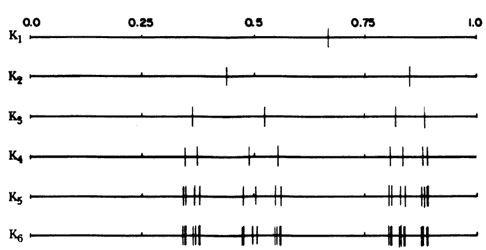
Figura 8. Bifurcaciones peri�dicas de la ecuaci�n log�stica.

TODO DEPENDE DEL INICIO

Una conclusi�n muy importante que se deriva del estudio del caos fue claramente descrita por Henri Poincar� en 1908. Este notable matem�tico franc�s, empleando las herramientas del c�lculo, escribi� la siguiente conclusi�n de sus trabajos sobre las ecuaciones que describen la evoluci�n temporal de varios sistemas: "una causa muy peque�a, que se nos escapa, determina un efecto notable que no podemos ver y decimos entonces que tal efecto se debe al azar."

Al referirse a la definici�n de las condiciones iniciales que deben emplearse (por ejemplo, en nuestro caso ser�a el valor dado a X en la ecuaci�n log�stica), nos dice que por mas que se trate de precisarlas, �stas ser�n siempre aproximadas y:

[...] puede suceder que peque�as diferencias en las condiciones iniciales engendren unas a�n mayores en el fen�meno final, un peque�o error en las primeras producir�a uno enorme sobre las segundas. La predicci�n se vuelve imposible y tenemos el fen�meno fortuito.

Para ver en la pr�ctica lo dicho por Poincar� debemos recurrir nuevamente a nuestra ecuaci�n. Empleando una K = 4.00 se calculan los resultados de las iteraciones con dos valores iniciales ligeramente diferentes entre s�, por ejemplo X = 0.4000 por una parte y X = 0.4001 por la otra. (El cuadro de la p�gina siguiente muestra algunos de los valores que se obtienen.)

Para la sexta iteraci�n la diferencia ha llegado al cuarto decimal, pero en la 21 est� ya en el primero, es decir que cualquier efecto, no importa lo peque�o que sea, alcanza proporciones macrosc�picas y la diferencia en los resultados crece exponencialmente. Una manera de obtener una medida de la sensibilidad de un sistema a las condiciones iniciales fue descrita por el matem�tico ruso A. M. Lyapunov (1857-1918). Supongamos que partimos de la ecuaci�n log�stica dando dos valores iniciales que difieren muy poco entre s�, por ejemplo, X y X + e, e iteramos la ecuaci�n n veces. Lyapunov encontr� que la divergencia puede caracterizarse aproximadamente por una f�rmula que nos dice que el valor de la diferencia iterada n veces es aproximadamente igual a e e^ln.

Núm. iteraciones	Valores de Xsig		Diferencia
0	0.4000	0.40001	-0.000010
6	0.025466	0.025261	0.000205
21	0.774403	0.554030	0.220373

La letra l es conocida como el exponente de Lyapunov, y nos da una velocidad promedio a la cual se separan las dos trayectorias. Si el exponente es negativo, las trayectorias poco separadas en el inicio tender�n a converger y la evoluci�n no ser� ca�tica. Por el contrario, si el exponente es positivo las trayectorias divergen y la evoluci�n es sensible a las condiciones iniciales y por tanto es ca�tica. En la figura 9 el exponente se grafica como funci�n del valor K de la ecuaci�n log�stica para valores entre 2.8 y 4.0. Si comparamos esta figura con la n�mero 5 observamos que el signo del exponente se correlaciona muy bien con el comportamiento del sistema, es decir, que los valores positivos corresponden a las bifurcaciones, mientras que los negativos se asocian al comportamiento peri�dico en la regi�n entre 3.5 y 4 del valor de K.

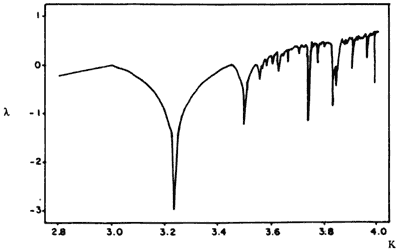
Figura 9. El exponente de Lyapunov vs. K para la ecuaci�n log�stica.

�D�NDE EST� EL PLANETA?

Quiz� el lector piense que exageramos la nota cuando hablamos de sistemas imposibles de predecir por su extrema sensibilidad a las condiciones iniciales. Para convencerlo de que estamos en lo cierto, veamos lo que sucede cuando se quiere conocer la posici�n futura de los planetas que constituyen el Sistema Solar. Siempre hemos tenido la idea de que el movimiento de los planetas es la imagen misma de la regularidad. Nuestro reloj c�smico se remonta a unos 5 000 000 000 de a�os, que es el tiempo estimado que ha transcurrido desde la creaci�n del Sistema Solar. La ley de Newton de la gravitaci�n universal permite modelar el movimiento de esos cuerpos, claro est�, introduciendo las correcciones necesarias debidas a la relatividad general para los planetas pr�ximos al Sol. La ley provee una relaci�n entre las aceleraciones de los cuerpos y sus posiciones. El sistema se puede modelar perfectamente si se conocen las condiciones iniciales en las que se introducen las coordenadas de posici�n y las de velocidad para un instante dado. Pero aun con esos datos la resoluci�n de las ecuaciones para estos sistemas no permite conocer las posiciones y velocidades para cualquier valor del tiempo. Tampoco arroja luz sobre c�mo var�an las trayectorias si uno modifica ligeramente las condiciones iniciales. El �nico ejemplo cuya soluci�n de ecuaciones da un valor exacto es el descrito para el caso de un planeta �nico que gira alrededor del Sol: el problema se puede integrar y la soluci�n indica que el planeta se mueve alrededor de una elipse. Sin embargo, en la pr�ctica los planetas describen movimientos m�s complejos debido a la perturbaci�n que introduce la atracci�n de los cuerpos celestes entre s� y la presencia de asteroides, cometas y otros objetos cuya existencia ignoramos. Gracias a los trabajos de Laplace y Lagrange referentes al estudio de la estabilidad del Sistema Solar se obtuvieron m�todos que permiten encontrar soluciones aproximadas a las ecuaciones de movimiento de los planetas, pero como fue demostrado por Poincar� tras sesudas demostraciones matem�ticas, los resultados no permiten conocer la estabilidad del sistema en periodos muy extensos. M�s recientemente, las computadoras han permitido hacer c�lculos que tiempo atr�s hubiesen tomado a�os de trabajo; as�, dos investigadores del Instituto Tecnol�gico de Massachusetts, Estados Unidos, realizaron la integraci�n de ecuaciones de movimiento de los planetas m�s externos de nuestro sistema para los pr�ximos 845 000 000 de a�os. La integraci�n num�rica indic� que Plut�n tiene un movimiento ca�tico. El exponente de Lyapunov se estim� a partir de la divergencia que ten�an las �rbitas, una de ellas especificada a partir de valores de referencia y la otra te�rica y muy pr�xima a la primera. La distancia que separa a las dos �rbitas se multiplica por un factor de tres cada 20 000 000 de a�os, lo que hace imposible cualquier predicci�n sobre la excentricidad y la inclinaci�n de la �rbita m�s all� de los 400 000 000 de a�os. En otra simulaci�n de los planetas internos (Mercurio, Venus, Tierra y Marte), J. Laskar, en Francia, lleg� a la siguiente conclusi�n: es posible precisar la posici�n de los planetas hasta 100 millones de a�os m�s, a partir de esta fecha las excentricidades e inclinaciones tienen una din�mica ca�tica, m�s a�n, un error de 0.00000001% en la estimaci�n de los valores iniciales aumenta a 100% en cien millones de a�os.

LAS MARIPOSAS DE LORENZ

En 1963 el meteor�logo Eduard Lorenz, interesado en obtener un modelo que predijera el clima, trabajaba con una computadora para desarrollar un sistema que simulara el complejo movimiento de la atm�sfera. El modelo hab�a sido simplificado al m�ximo: una capa de aire pr�xima a la superficie se eleva por el calentamiento que le provoca la radiaci�n solar absorbida en el suelo. El programa de c�lculo inclu�a un conjunto de tres ecuaciones diferenciales cuyas variables representaban el movimiento, la variaci�n horizontal y vertical de la temperatura. Lorenz pidi� a la m�quina que a partir de ciertos valores iniciales que �l propuso, calculara los datos correspondientes para diferentes intervalos, por medio de iteraciones como las que ya describimos. Cada uno de los resultados fue impreso en una gr�fica de tres ejes (X, Y, Z) y cada uno representa una de las variables del modelo. Para su asombro, los valores obtenidos formaron una figura parecida a una mariposa con sus alas desplegadas, v�ase la figura 10.

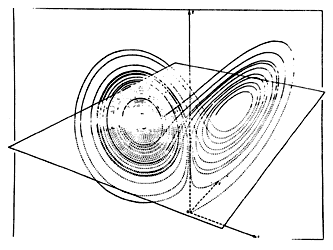
Figura 10. El atractor de Lorenz.

Los resultados de Lorenz, a pesar de haber aparecido en una revista t�cnica, pasaron inadvertidos para la comunidad cient�fica. La figura del modelo de Lorenz no es otra cosa que la manifestaci�n de la inestabilidad exponencial. En meteorolog�a se sabe que la amplitud de una perturbaci�n se duplica cada tercer d�a. A una condici�n inicial dada, es decir, cierto estado de la atm�sfera en la superficie del planeta (presi�n, temperatura, humedad) le corresponde una evoluci�n futura perfectamente determinista. No obstante si se modifican ligeramente las condiciones iniciales, por ejemplo, si alg�n miembro poderoso de La Compa��a, del cuento de Borges, hace que una mariposa agite sus alas, este peque�o cambio tal vez no tenga repercusiones en los primeros instantes o d�as. Sin embargo, ya lo hemos visto con las iteraciones, la modificaci�n se amplificar� y si se duplicar� cada tercer d�a, se multiplicar� por 300 cada mes y por 100 000 cada dos meses y llegar� a ser 10³⁰ por a�o.

Si reflexionamos sobre los hechos anteriores vemos tambi�n que en los sistemas ca�ticos existe una p�rdida de informaci�n con el paso del tiempo. Si uno conoce el estado de un sistema con N decimales en el tiempo inicial, t = 0, �nicamente podremos conocer N - 1 en el instante siguiente t = 1, y por tanto N - n en el instante t = n hasta perder toda la informaci�n anterior cuando t = N. Esto es parte de las caracter�sticas de la inestabilidad exponencial: los errores se multiplican hasta degradar toda la informaci�n de partida. Para un sistema que posee esta propiedad, sea unidimensional como el caso de la ecuaci�n log�stica o multidimensional y complejo como es la atm�sfera, la din�mica misma es la �nica capaz de revelarnos la informaci�n que estaba contenida en las condiciones iniciales. En el caso de la meteorolog�a esto quiere decir que el tiempo que observaremos dentro de un a�o revelar� informaci�n sobre el estado de la atm�sfera que prevaleci� hoy. Consid�rese que las medidas que se determinan en las ciencias experimentales nunca son definidas m�s all� de la incertidumbre ligada a la medici�n, y los instrumentos m�s precisos que poseemos hoy en d�a nos dan valores que no pasan de las doce cifras, l�mite de precisi�n para las constantes físicas. Visto desde otro �ngulo, cuando la din�mica del sistema ca�tico nos permite conocer la treceava cifra revela una nueva informaci�n creada de la nada. De lo anterior se resume que la evoluci�n futura de tal sistema depende del estado que podemos constatar en este momento... �y del azar!, aunque es claro que siempre tenemos el recurso de echar mano de las leyes de c�lculo de probabilidades que permiten estimar el comportamiento promedio de dichos sistemas en el tiempo. Por tanto, la definici�n tradicional de un sistema azaroso, mejor dicho estoc�stico, s�lo puede ser descrita en t�rminos de propiedades promedio dadas por una distribuci�n probabil�stica determinada. �Se puede diferenciar desde ese punto de vista una secuencia aleatoria de la generada por el caos determinista? Veamos un ejemplo sencillo de este problema; utilizaremos una ecuaci�n que nos permite calcular el valor siguiente a partir del que le precede:

Xsig= 1- K X2

(ecuaci�n 3)

Digamos que inicialmente X vale 0 y K siempre vale 1.5, invitamos al lector a realizar el c�lculo de los primeros doce resultados. Ahora reemplacemos por A aquellos valores cuyos resultados son menores de cero y por B los mayores de cero. La serie obtenida se escribir�: B A B B B B B A B B B A. Ahora t�mese una moneda y an�tese las veces que cae �guila, que llamaremos A, y las que cae sol, que denominaremos B. Supongamos que la secuencia obtenida es: A B B A B B A A B A B A. Para una persona que no sea muy observadora, la primera secuencia obtenida a partir de una ecuaci�n muy sencilla le parecer� muy similar a la de la moneda, ya que no puede especular cu�l ser� el valor siguiente a partir de la secuencia de d�gitos que tiene ante s�. Comprobar que una serie es rigurosamente aleatoria no es tarea f�cil y los matem�ticos someten los resultados a pruebas estad�sticas exhaustivas para estar seguros de ello. Se podr�a pensar que lanzar la moneda resulta la manera m�s cl�sica de producir una serie de n�meros aleatorios, pero en el fondo no es as�, ya que, por ejemplo, si lanzamos la moneda 20 veces se puede generar 2²⁰ (es decir, un poco menos de un mill�n) series binarias de secuencias y cada una de ellas con la misma posibilidad de hacerse presente. Por lo tanto, seg�n la definici�n t�cnica de caos, un sistema din�mico ca�tico es aquel que exhibe muchos de los atributos de los sistemas ideales aleatorios; en esencia su evoluci�n es impredecible debido a la extrema sensibilidad a las condiciones iniciales y el promedio de sus propiedades se puede describir empleando m�todos estad�sticos.

Si quisi�ramos transmitir a una persona la secuencia de A y B que surge de la ecuaci�n log�stica en la zona ca�tica, y no conoci�ramos la f�rmula que dio origen a los valores, emplearemos una computadora y le dar�amos un programa de instrucciones (un algoritmo) a fin de que la m�quina pudiera reproducir paso a paso dicha secuencia en forma expl�cita sin que tuviera que comprender el resultado de cualquier parte de la informaci�n que proporciona. Los cient�ficos A. N. Kolmogorov y G. J. Chaitin han definido que una serie de n�meros es aleatoria si el algoritmo m�s peque�o que se le puede especificar a la computadora tiene el mismo n�mero de bits (1 bit es la unidad fundamental de informaci�n) que la propia serie.

Por lo tanto, una manifestaci�n de la incapacidad de predecir la din�mica de un sistema ca�tico es que su evoluci�n en el tiempo es computacionalmente irreducible. La manera m�s r�pida de saber c�mo prosigue la din�mica de un sistema ca�tico es observando su evoluci�n. Ve�moslo de esta manera: supongamos que se realiza la simulaci�n mediante una serie de n�meros binarios de la evoluci�n del sistema de Lorenz. Un cient�fico intentar� explicar estas observaciones por medio de una teor�a que puede verse como el algoritmo capaz de generar la serie de resultados y extenderla, es decir, predecir las observaciones futuras. Para una serie dada de observaciones siempre existir�n otras teor�as que compiten entre s� y el cient�fico tendr� que escoger entre ellas. El modelo que se escoja tendr� la menor cantidad de bits. Entre m�s peque�o es el programa, m�s se comprende el fen�meno que se estudia. El hecho es que los resultados de la simulaci�n del fen�meno meteorol�gico no pueden ser predichos, por lo que cabe hacer la reflexi�n de si existen realmente sistemas azarosos ideales en el mundo de la f�sica cl�sica o m�s bien la aparente aleatoriedad que observamos y explotamos en las teor�as estad�sticas no es otra cosa que el comportamiento ca�tico de alg�n sistema din�mico determinista escondido.

El drag�n en la mitolog�a mesopotámica se asocia con el caos. La serie de 10 diapositivas que aqu� se presenta fue generada y coloreada por el doctor Isaac Schiffter. La n�mero 5 representa una alegor�a entre el caos y el orden (estructura del acr�lico).

LOS DIAGRAMAS DE FASES

Volvamos a la figura generada por la computadora de Lorenz, �qu� es lo que representa? Para entenderla es necesario describir c�mo se representa la din�mica de un sistema en forma geom�trica. El sistema din�mico est� caracterizado por dos elementos: un estado y una din�mica. El primero representa las variables que lo caracterizan y el segundo es una regla que describe la forma en que el estado evoluciona, por ejemplo con el tiempo, para lo cual los cient�ficos utilizan una construcci�n en un espacio matem�tico llamado de fases. Veamos c�mo se puede representar el movimiento de un p�ndulo que se balancea suavemente en ausencia de fricci�n. Si construimos un diagrama de fases en el cual las variables son de posici�n y velocidad, el vaiv�n quedar� descrito por un punto en el plano. En su eterno ir y venir, el p�ndulo seguir� una �rbita o camino en un espacio de fases, en la figura 11 se representa uno en forma bidimensional, la L corresponde a la posici�n y V a la velocidad. Despu�s de ser lanzado, la oscilaci�n infinita describe una trayectoria que tiene forma de elipse representada peri�dicamente por el punto representativo.

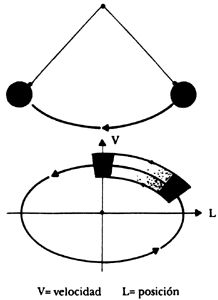
Figura 11. Movimiento de un p�ndulo sin fricci�n en el espacio de fases: V = velocidad, L = posici�n.

Despu�s de cierto tiempo, el conjunto de puntos iniciales contenidos en el cuadrado se�alado en la figura se vuelve a encontrar dentro de otro cuadrado de �rea id�ntica al primero. Ahora supongamos que el p�ndulo oscila experimentando una resistencia a su movimiento, por ejemplo, la que ocasiona la fricci�n de sus partes con el aire. Esto produce que al cabo de un tiempo pierda su impulso y termine por detenerse; en el espacio de fases la din�mica quedar� descrita por una espiral, la cual se va contrayendo sobre s� misma hasta terminar en un punto fijo, cuando llega al equilibrio. Obs�rvese la figura 12, el �rea que contiene los puntos iniciales se contrae hasta reducirse a un punto. Hasta la aparici�n de las m�quinas de cuarzo, los relojeros hab�an empleado al p�ndulo como referencia del tiempo. Dado que no se puede eliminar completamente la fricci�n, se debe proporcionar al balanc�n cierta energ�a para mantener su movimiento, por ejemplo mediante pesas.

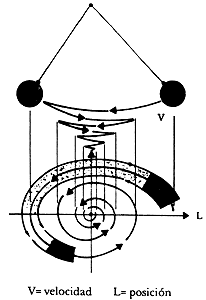
Figura 12. Movimiento de un p�ndulo con fricci�n en el espacio de fases. V = velocidad, L = posici�n.

El movimiento de ese balanc�n corresponde tambi�n a una trayectoria el�ptica en el espacio de fases, pero diferente a la del ejemplo anterior: sin importar el impulso que se le d� al inicio, el balanc�n, al cabo de un lapso realizar� un movimiento que siempre tiene la misma velocidad y amplitud. En el espacio de fases, una trayectoria que se inicia del interior o del exterior de la elipse terminar� por acercarse a ella y confundirse. Dicha elipse se llama de ciclo l�mite y es tambi�n un atractor. Resumiendo, los dos tipos de atractores se caracterizan por tener �rbitas o trayectorias que no se repiten exactamente en el tiempo, pero que se mantienen muy pr�ximas unas de las otras, llegando a concurrir en el mismo punto fijo o ciclo l�mite. En los dos casos, el comportamiento de los sistemas es predecible cuando la amplitud del movimiento es moderada. Pero el espacio de fases puede tener m�s de dos dimensiones y en esos casos la din�mica del sistema es mucho m�s compleja y aparecen los atractores llamados extra�os.

ATRACTORES SORPRENDENTES

El atractor de Lorenz, tal y como se le conoce hoy en d�a, es el resultado del comportamiento ca�tico al tratar de modelar el movimiento de una capa de aire en un sistema tridimensional. Imaginemos por un momento que tenemos la capacidad de observar los atractores a intervalos constantes de tiempo (podr�amos pensar en intervalos a cierto n�mero de iteraciones de las ecuaciones que describen el sistema). Cuando el atractor tenga un solo periodo, cada vez que analicemos la figura encontraremos un punto que representa el estado del sistema en el mismo sitio de la iteraci�n previa, como el caso del p�ndulo que oscila sin resistencia a la fricci�n. Sin embargo, puede suceder que el punto no regrese a su posici�n original en el espacio de fases, y cada vez que realicemos la observaci�n veremos que "viaja" en forma err�tica confinado en un espacio de fases, creando una miríada de puntos que reflejan trayectorias; al inicio son muy pr�ximas pero en el curso de las iteraciones se alejan vertiginosamente. Dado que en el espacio de fases las �rbitas no pueden distanciarse eternamente, en un determinado momento se pliegan sobre sí mismas, operaci�n que repiten una y otra vez.

�Cu�l es el factor que determina este fen�meno? Con anterioridad se demostr� que una de las caracter�sticas esenciales de los fen�menos ca�ticos es su sensibilidad a las condiciones iniciales; basta una peque�a incertidumbre en la definici�n de ellas para que el error se magnifique r�pidamente con el tiempo y sea imposible prever en d�nde se colocar�n los puntos en la gr�fica. Stephen Smale, matem�tico de la Universidad de California, demostr� gr�ficamente el proceso din�mico que sucede en los atractores extra�os, empleando conceptos de topolog�a. Esta rama de las matem�ticas estudia las deformaciones continuas en geometr�a y las relaciones entre las teor�as de las superficies y el an�lisis matem�tico. Vemos en la figura 13 c�mo se representa la gestaci�n del atractor extra�o. Primero nos procuramos un material estirable y con �l trazamos un cuadrado que representa el espacio de fases (figura 13 (A)). Luego estiramos esa figura para obtener un rect�ngulo (figura 13 (B)), el cual doblamos para generar algo as� como una herradura (figura 13 (C)). Hasta aqu� lo que hemos hecho es equivalente a realizar una iteraci�n de la ecuaci�n; consid�rese que ahora dos puntos, inicialmente alejados, son pr�ximos. Procedamos a confinar la herradura en el espacio de fases original (figura 13 (D)) y realicemos una manipulaci�n id�ntica a la anterior. Aparecen cuatro peque�os rect�ngulos (figura 13 (E)), que se ir�n multiplicando conforme se hagan m�s iteraciones y todos ellos provienen de �rbitas que surgen de estados iniciales totalmente diferentes. Cuando se amplifica cualquier punto de la imagen del atractor de Lorenz (por ejemplo, haciendo c�lculos m�s precisos) veremos que el objeto tiene peque�as copias de s� mismo, perfectas en cada detalle, de manera que una parte del mismo es semejante al conjunto total a diferentes escalas de amplificaci�n; m�s claramente dicho es un fractal. Cuando uno clasifica los objetos cl�sicos de la geometr�a dentro de una escala de 1 a 3, los puntos quedan incluidos en el primer grupo y su dimensi�n es cero, las curvas son de dimensi�n uno, las superficies dos, y los s�lidos de dimensi�n tres. Los fractales, naturalmente, se sit�an en posiciones intermedias; por ejemplo, el atractor de Lorenz se sit�a entre 2 y 3. Dado que el n�mero de valores necesarios para describir el atractor es de tres, el hecho de que la dimensi�n del atractor sea inferior significa que el sistema no explota todo el espacio te�ricamente disponible. Una explicaci�n muy clara de los fractales se encuentra en el libro de E. Braun, Un movimiento en zigzag (La Ciencia desde M�xico, n�m. 13).

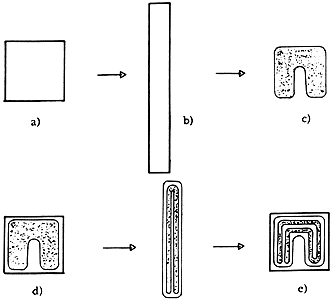
Figura 13. Construcci�n del mapa de la herradura de Smale para dos iteraciones.

LA TURBULENCIA

Despu�s de esta excursi�n por el mundo de las matem�ticas y los atractores extra�os es conveniente tomar un respiro y relajar la mente, para lo cual invitamos al lector a irse de pesca. El movimiento del agua nos hipnotiza mientras intentamos burlar al pez y atraparlo. Si para observar el curso de las aguas tomamos como referencia la vegetaci�n que viaja por ellas, notamos que en las zonas tranquilas las hojas parecen moverse en l�nea recta y a la misma velocidad. En cambio, en los r�pidos las velocidades son diferentes y si seguimos el movimiento de dos hojas que en un momento viajan pr�ximas, veremos que s�bitamente se apartan describiendo trayectorias que no repiten las que vienen atr�s. Se dice que en esta �ltima zona el agua es turbulenta. La hidrodin�mica se interesa en el comportamiento de los fluidos en movimiento y la turbulencia en particular sigue siendo un problema no del todo resuelto desde el punto de vista te�rico, ya que hasta hace no muchos a�os no hab�a una descripci�n rigurosa y precisa para el mecanismo por el cual un fluido pasa de un movimiento ordenado a otro turbulento. El estudio de estos mecanismos tiene un alto valor desde el punto de vista cient�fico y tecnol�gico; baste recordar que gran parte del transporte que realiza el ser humano es a base de ductos, adem�s de que existen sistemas, como las turbinas o los aviones y barcos, que se mueven en un fluido. �C�mo imitar el movimiento de los delfines que se desplazan retardando al m�ximo la formaci�n de la turbulencia? Algo tiene que ver la compleja estructura de su dermis y epidermis y cuando podamos imitarla seguramente economizaremos grandes cantidades de energ�a que gastamos en la propulsi�n de barcos y submarinos. Pero este no es el �nico campo que se beneficiar�a con el conocimiento m�s detallado de la turbulencia; como el cuerpo humano posee una vasta red de ductos por los cuales circula la sangre, el conocimiento de las pautas de movimiento sin duda aclarar�a muchos de los problemas circulatorios que se presentan.

Seg�n nos cuenta E. Braun en su libro Un movimiento en zigzag, el bot�nico Robert Brown hab�a realizado una descripci�n muy parecida en 1827, al observar al microscopio una suspensi�n de polen en agua. A cualquier escala de tiempo, por peque�a que fuese, la part�cula cambiaba constantemente de direcci�n y de velocidad. Despu�s de los trabajos de Maxwell, y sobre todo los de Einstein y Perrin, realizados medio siglo despu�s, se hizo claro que el movimiento browniano no era sino el efecto visible que resultaba del choque de las mol�culas de agua con la part�cula de polen. Seg�n el modelo que se desarroll�, despu�s de cada colisi�n se pierde la informaci�n sobre las velocidades adquiridas en el choque previo, por tanto ya no son correlacionables la velocidad y la posici�n entre s�, y s�lo es posible conocer una distribuci�n promedio de velocidades.

En el caso de la turbulencia su descripci�n tambi�n es estad�stica, ya que es imposible predecir la velocidad exacta de un fluido en un punto dado. M�s a�n, lo �nico que puede uno predecir es la probabilidad de que la velocidad tenga cierto valor, aunque esto tambi�n tiene dificultades ya que se sabe que las velocidades fluct�an cuando el movimiento es turbulento, pero no se conoce con precisi�n cu�l es la ley de probabilidad que hay que aplicar.

Pero vayamos del orden al desorden y primero describamos aquel flujo de fluido que no es turbulento. Supongamos que tenemos un l�quido viscoso que queremos desplazar por un tubo; la viscosidad, entendida como el rozamiento interno del fluido, hace necesario que ejerzamos una fuerza para obligar a la capa l�quida a deslizarse sobre otra. Si la velocidad no es muy elevada, el movimiento del l�quido ser� laminar, en cuyo caso imaginamos que todas las mol�culas del fluido se mueven como los coches en una autopista de m�ltiples carriles de acuerdo con las siguientes reglas: a) cada coche sigue el mismo camino que sus predecesores; y b) dos coches vecinos que est�n en el mismo carril o en uno diferente, conforme pasa el tiempo se separan lentamente uno de otro, en forma proporcional a la diferencia de velocidades, esto es, linealmente. Sin embargo, cuando el fluido es sacudido por alguna fuerza externa y la velocidad excede un valor cr�tico, la naturaleza del movimiento es impredecible, aparecen torbellinos que originan un aumento a la resistencia al movimiento. Esa transici�n entre los dos estados tiene causas que no son conocidas aun cuando sabemos emp�ricamente cu�les son los factores que determinan si el r�gimen de un fluido ser� laminar o no. �C�mo estudiar experimentalmente la turbulencia sin introducir en el sistema dispositivos que perturben la observaci�n? La estrategia es sencilla y se basa en poner en movimiento el fluido mediante la convecci�n t�rmica. En t�rminos menos t�cnicos, consiste en crear una diferencia de temperatura en un material que se expande, lo que provoca el movimiento del mismo. Este experimento lo realiz� el franc�s Henri B�nard en 1900, encontrando resultados verdaderamente interesantes.

LAS C�LULAS DE B�NARD

Henri B�nard fue uno de los cient�ficos pioneros en el campo de la hidrodin�mica. Empleando el principio de la convecci�n se propuso estudiar el movimiento de l�quidos viscosos, para lo cual dise�� un sistema en el que calentaba un recipiente por abajo en forma controlada mediante placas perpendiculares al eje gravitacional. En la figura 14 mostramos el equipo experimental que B�nard construy� para realizar sus observaciones; se trata de un cilindro perfectamente aislado para evitar la p�rdida de calor por las paredes laterales. Al calentar las placas mediante vapor de agua, entre la parte inferior del recipiente y la superior se establec�a una diferencia de temperatura que se manten�a constante. En esas condiciones el calor genera una expansi�n del l�quido, provocando que el fluido m�s caliente tenga una densidad menor, por lo que tender� a subir mientras el superficial har� lo contrario. En el experimento original, B�nard emple� una capa delgada de aceite de ballena, quedando la superficie superior en contacto con el aire. Para estudiar la convecci�n utiliz� como detector "un corp�sculo s�lido, de densidad igual a la del l�quido, el cual tiene el mismo movimiento de la part�cula l�quida que reemplaza, a condici�n de que el grano tenga dimensiones despreciables": en este caso fueron granos de licopodio. Tomando placas fotogr�ficas en distintos momentos observ� que bajo condiciones de calentamiento precisas el l�quido sub�a por el centro del recipiente, mientras que el de la superficie descend�a por los bordes, tal como se muestra en la figura 15.

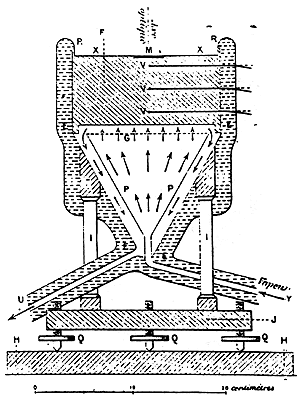
Figura 14. El equipo empleado por B�nard (del dibujo original).

Figura 15. Esquema descrito por B�nard para explicar la formaci�n de las "celulas".

Como los granos de licopodio son menos densos que el fluido no se sumergen, por lo tanto, cuando B�nard a�adi� el polvo y esper� cierto tiempo, lo que observ� aparece en la figura 16: s�bitamente se generan en forma espont�nea estructuras hexagonales de ejes verticales, que "es la estructura celular regular. Llamar� en lo subsiguiente c�lula al volumen limitado por uno de esos prismas verticales". Adem�s nos dice: "�nicamente por la acci�n de fuerzas moleculares ordinarias y de la gravitaci�n, una capa l�quida muy delgada, inicialmente homog�nea, se puede dividir en individuos l�quidos, todos iguales, limitados por prismas hexagonales regulares."

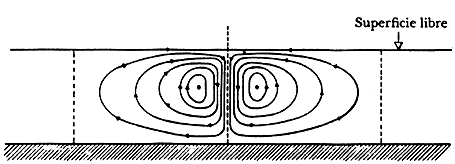
Figura 16. Las c�lulas del experimento de B�nard.

B�nard tambi�n insiste en el hecho de que la m�nima perturbaci�n t�rmica o mec�nica, como podr�an ser las corrientes de aire, provoca la ruptura de la formaci�n. B�nard llega a conclusiones interesantes: "En lo que concierne a la posible relaci�n con la estructura de los seres organizados, temo aventurarme sobre un terreno que no me es familiar, si trato de precisar los detalles..." B�nard sugiere que la divisi�n celular podr�a llevarse a cabo por fen�menos de difusi�n o de �smosis que produzcan los mismos efectos que el calor provoc� en el caso que �l estudi�.

EL HELIO EN CONVULSI�N

En a�os recientes se llev� a cabo un experimento m�s controlado que el de B�nard, en el cual el fluido empleado fue el helio gaseoso a baja temperatura, es decir a 268� C bajo cero. El material estaba dentro de un cilindro vertical, confinado entre dos placas, al cual se calentaba por abajo y se enfriaba por arriba. Durante la experiencia el par�metro que se vari� fue el llamado n�mero de Rayleigh (Ra), bautizado as� en honor de Rayleigh, otro de los notables pioneros en el estudio de la hidrodin�mica, que en 1916 public� sus trabajos y dio una primera interpretaci�n del fen�meno.

El Ra, en t�rminos sencillos, es una medida adimensional de la diferencia de temperatura impuesta al sistema, pero depende de otras caracter�sticas del fluido como son la viscosidad, la conductividad t�rmica, etc. Cuando el Ra es peque�o se presenta un fen�meno de conducci�n, es decir, el calor se transmite sin que el fluido se mueva, y mediante term�metros colocados entre la parte inferior y superior se verifica que hay un gradiente de temperatura constante en el tiempo. Cuando el valor de Ra es un poco m�s elevado, el fen�meno pasa a ser de tipo convectivo y aparecen las c�lulas de B�nard. Si se prosigue el calentamiento, el movimiento del fluido no es del todo desordenado; por el contrario, se establece una estructura regular en forma de rodillos (v�ase la figura 17) en la que es posible observar una sucesi�n de corrientes que suben y bajan alternadamente, y son casi equidistantes cuando se establece una diferencia de temperatura entre T y T + § T. En la figura se aprecia que la distancia entre dos corrientes verticales adyacentes es del orden de d, que es la distancia entre dos placas r�gidas horizontales. Debe se�alarse asimismo que si consideramos todo el conjunto de rodillos veremos que cada uno de ellos puede cambiar el sentido de su giro sin que con esto se modifiquen las propiedades geom�tricas o din�micas del fluido en movimiento. Esto se debe a que la probabilidad de que gire en un sentido o en el otro es exactamente la misma, como sucede cuando dejamos caer una piedra desde la cima de una monta�a, puede rodar por uno u otro lado de la ladera. Si se aumenta el Ra a�n m�s, las c�lulas se desordenan y aparece el caos, los term�metros marcan temperaturas totalmente aleatorias y el fluido tiene un comportamiento tan err�tico que pareciera que cada una de sus partes se desplaza en forma independiente. En tal caos aparente, los cient�ficos han podido describir, adem�s de las estructuras de B�nard, otras formaciones curiosas como: a) las llamadas capas l�mite, las cuales son regiones muy delgadas de espesor en donde la velocidad del fluido varia r�pidamente; y b) las plumas t�rmicas, especie de hongos parecidos a los que se desarrollan en una explosi�n nuclear, los cuales son resultado de la existencia de una fuente de calor puntual en el fondo del recipiente. El fluido caliente sube por el pie del hongo y cuando alcanza el sombrero se extiende antes de volver a descender. Estas formaciones las encontramos en otros contextos, por ejemplo en las turbulencias que se sienten a veces cuando se viaja en avi�n; se piensa tambi�n que la erupci�n de la lava durante una actividad volc�nica sigue el mismo principio.

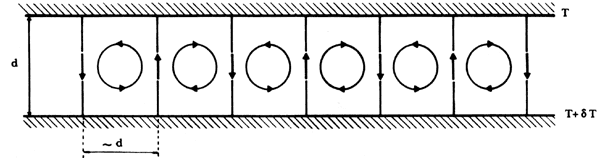
Figura 17. Diagrama de la organizaci�n del movimiento de un fluido en convexi�n.

EL AGUA TAMBI�N ES DESORDENADA

En la Universidad de Chicago, que ha sido sede de los estudios recientes en turbulencias; tambi�n se ha trabajado usando como modelo el agua. �Cu�ntas veces la hemos calentado sin percatarnos de la gran complejidad de los movimientos que se generan! Consideramos interesante transcribir la descripci�n de los autores que realizaron un experimento en un recipiente de unos veinte cent�metros de alto, el cual calentaban por abajo y enfriaban por arriba, tal como lo hac�a B�nard. Nos dicen los cient�ficos que el agua gira en sentido inverso a las manecillas de un reloj y que en ciertas regiones del recipiente el l�quido se acelera antes de subir r�pidamente como un chorro, el cual atraviesa la parte superior y desciende tambi�n en forma de chorro hacia el fondo; esto parecer�a una gran c�lula de B�nard. Paralelamente, cerca del fondo del recipiente se observan regiones de capas l�mite en donde el l�quido est� relativamente en calma, �pero con una temperatura mayor que el resto!, y a la m�nima perturbaci�n emergen las plumas t�rmicas de estas regiones. Todo este concierto de formas y movimientos, paradoja de la turbulencia, parece llevarse a cabo en zonas independientes. Sigue en pie la pregunta que surge de la turbulencia: �cu�l es el mecanismo por el cual se origina? La respuesta no es a�n contundente y posiblemente pasar� mucho tiempo antes de obtenerla; lo que s� podemos decir es que estudios detallados de estos experimentos comprueban que se genera un mecanismo muy semejante al que hemos visto anteriormente con la ecuaci�n log�stica. La explicaci�n m�s avanzada hasta la fecha fue dada en 1978 por D. Ruelle y F. Takens en Francia, y es de gran importancia ya que echa por tierra el mecanismo del investigador ruso, Lev Landau que hab�a prevalecido por muchos a�os. Tal y como vimos en la ecuaci�n ca�tica, despu�s de una etapa determinista aparecen bifurcaciones en los valores y la ecuaci�n empieza a oscilar.

De acuerdo con Landau, para que ocurra la turbulencia es necesario que suceda un n�mero muy elevado de bifurcaciones para llegar a ese estado; Ruelle y colaboradores han demostrado que s�lo unas cuantas oscilaciones son necesarias para entrar en caos. M�s a�n, en Italia, V. Fraceschini, mediante un sistema de cinco ecuaciones diferenciales acopladas, adapt� en su computadora las ecuaciones que rigen el movimiento del fluido y encontr� que aparec�an los atractores de bifurcaci�n peri�dica conforme los elementos que gobiernan el movimiento se acercaban a los valores que irrumpen en el r�gimen turbulento. Los c�lculos de su simulaci�n indicaron que los n�meros descubiertos por Feigenbaum se comprobaban perfectamente. Por primera vez un modelo matem�tico de la turbulencia f�sica revelaba una parte de su compleja estructura.

CAOS Y MEZCLAS

"...Con las manos o utilizando un tenedor se desbarata la levadura en harina, agreg�ndole media taza de leche tibia. Cuando est�n bien incorporados los ingredientes se amasan un poco, se forma una bola y se deja reposar..., reza la receta para hacer una rosca de reyes, �y es precisamente en la mezcla de los componentes que est� el secreto de la pasta! Tambi�n los qu�micos necesitan de una buena mezcla para que las reacciones procedan eficientemente, o para dispersar los dep�sitos que obstaculizan una tuber�a. Sin importar el proceso de que se trate, la mezcla es una operaci�n compleja y hay que elegir entre fluidos que puedan o no ser totalmente miscibles entre s�, o que fluyan lenta y ordenadamente o r�pido y en forma turbulenta. La parte principal en la comprensi�n de los fen�menos b�sicos del mezclado se basa en el concepto del "movimiento", una idea que fue desarrollada en el siglo XVIII por el matem�tico suizo Leonhard Euler. Desde el punto de vista matem�tico, el movimiento de un fluido es una expresi�n que nos permite conocer en d�nde estar� cada part�cula del fluido para un tiempo futuro; de esa manera se podr� calcular la fuerza y energ�a total necesaria para realizar cierta cantidad de mezclado en el sistema. Dada la dificultad que implica poseer dicha informaci�n, una manera de conocer el mecanismo por el cual se lleva a cabo el proceso de mezclado consiste en realizar el estudio en un sistema de dos dimensiones. Al generar un mapa de espacio de fases bidimensional mediante una computadora, el sistema queda restringido en sus movimientos y las part�culas adoptan uno de dos comportamientos: o fluyen por el mismo camino creando una corriente (una �rbita, dir�amos si estuvi�semos hablando de la ecuaci�n log�stica) o se quedan est�ticas. �C�mo hacer para que las corrientes lleguen a un punto com�n, se separen luego y posteriormente se aproximen de nuevo para volver a mezclarse? La respuesta la sabe intuitivamente quien cocina sin tanta matem�tica: hay que forzar el flujo para que var�e con el tiempo en una forma peri�dica de manera que se estire y se pliegue como el atractor de Smale para que parte de la mezcla regrese al punto de origen. Es posible relacionar el estudio del tipo de atractores que se generan con la eficiencia del mezclado. Debemos pensar que el atractor generado es del tipo de ciclo limitado, por ejemplo, y el fluido regresa a su posici�n original, veremos en la mezcla de dos componentes islas de un material rodeado por el otro, lo cual obstaculiza la homogeneidad del fluido. En la figura 18 se representa una simulaci�n por computadora de cierto n�mero de "part�culas" que se mezclan al moverse entre dos cilindros exc�ntricos que giran peri�dicamente en sentido opuesto. La computadora calcula el movimiento que se genera en cada giro y en este caso representa 1 000 de ellos; como se ve, la mezcla es bastante homog�nea aunque todav�a hay un par de islas de material que no se ha mezclado. J. Ottino y K. Leong de la Universidad de Massachusetts, EUA obtuvieron las im�genes de la figura 19 como resultado de un experimento de laboratorio; en ellas se demuestran con claridad el proceso de deformaci�n y plegamiento descrito por Smale. En este caso se trata de un material fluorescente, el cual deposita en la superficie de la glicerina un producto viscoso, que se encuentra en una cavidad rectangular. La parte superior e inferior de la c�mara se mueven independientemente y en este caso en forma peri�dica, pero discontinua. Se observa que conforme aumenta el n�mero de periodos aparece el mecanismo de deformaci�n y plegamiento, que conduce al mezclado ca�tico necesario para obtener un material final homog�neo.

Figura 18. Simulaci�n computacional de una mezcla de "part�culas", en donde a�n aparecen zonas heterog�neas.

Figura 19. Secuencia de deformaci�n y plegamiento en un experimento de mezclado.