III. CAOS Y BIOQUÍMICA
SI LAS reacciones catalíticas que se llevan a cabo en un reactor
industrial pueden presentar, bajo ciertas condiciones, dinámicas complejas,
¿qué pasa en el complejo reactor catalítico que es nuestro cuerpo? Por lo general,
la composición química de un adulto se mantiene constante, y si bien uno renueva
constantemente sus estructuras, las reacciones que se producen en su seno son
necesariamente alimentadas por sustancias que la persona toma del exterior.
Estas sustancias son el oxígeno y los alimentos. En condiciones extremas, los
alimentos en presencia del oxígeno se queman para darnos productos termodinámicamente
estables, como el bióxido de carbono y el agua. Pero en nuestro cuerpo reaccionan
a la temperatura ambiente con el oxígeno en presencia de catalizadores
muy eficientes: las enzimas. Por acción de ellas los animales, por ejemplo,
transforman el oxígeno y la mayoría de los alimentos en gas carbónico y agua,
pero este paso se acompaña de otro en el cual parte de las sustancias se convierten
en los materiales de los cuales están constituidos los seres, que no son el
producto final que dicta la termodinámica del proceso. Obviamente estas últimas
(llamados productos metaestables), se convertirán en los productos más estables,
lo cual permitirá la producción de trabajo o simplemente de calor. Si todas
las reacciones que conducen al equilibrio termodinámico están acompañadas de
un aumento de la entropía del sistema, es decir, de una degradación del orden
que le caracteriza, podría parecer contradictorio el hecho de que se generen
estructuras tan ordenadas como las que poseen los seres vivientes. Durante mucho
tiempo prevaleció la idea de que las reacciones bioquímicas inevitablemente
convergían de inmediato a un estado termodinámicamente estacionario y que éste
era único. Gracias a los trabajos de Prigogine, ya mencionados con anterioridad,
se demostró que en un sistema abierto que intercambia energía y materia con
el medio exterior, en el caso de que los suministros externos sean suficientemente
grandes, el sistema puede tender hacia un régimen constante que no es precisamente
el del equilibrio. Se trata de un estado estacionario no equilibrado y se relaciona
con lo que se ha dado en llamar estructuras disipativas, es decir, estructuras
que se crean y se mantienen gracias a intercambio de energía con el mundo exterior
en condiciones de no equilibrio. Ya hemos mencionado que las células de Bénard
son un ejemplo clásico de estructura disipativa de tipo especial, y la de Belousov-Shabotinsky
representa además una estructura temporal; veamos la representación del mecanismo
más sencillo de una reacción catalítica en el nivel bioquímico, en este caso
para una enzima que transforma un sustrato inicial en un producto dado:
| E |
||
| S |
® |
P |
La transformación se lleva a cabo por una secuencia de pasos que fue descrita por dos químicos alemanes, Michaelis y Menten en 1913. El ciclo lo podemos describir mediante el esquema que está representado en la figura 33. En él aparecen por lo menos tres intermediarios: una enzima libre (E), un complejo entre la enzima y el sustrato (ES) y un complejo entre la enzima y el producto (EP) para por último generar el producto de la reacción y liberar la enzima que reanuda el ciclo.
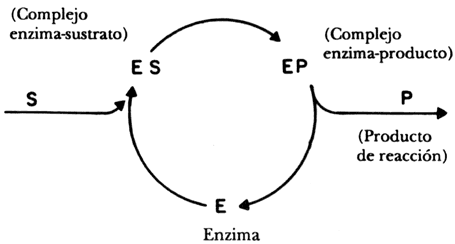
Figura 33. El ciclo de una reacción catalizada por enzima (E); S = sustrato; complejo enzima- sustrato (ES) y enzima- producto (EP); P = producto de reacción.
Veamos ahora uno de los famosos ciclos de reacción que se llevan a cabo en el nivel bioquímico en muchos sistemas biológicos. Nos referimos al llamado ciclo glicolítico; en él la conversión del adenosín-trifosfato (ATP) en adenosín-ifosfato (ADP) y viceversa, desempeña un papel preponderante para almacenar y disponer la energía en los seres vivos. La glucosa constituye una materia prima importante en este proceso. Los productos finales dependen del organismo en particular y la disponibilidad de oxígeno, pero en todos los casos las primeras etapas del proceso se inician con la conversión de la glucosa en piruvato con ganancia neta en ATP. Las moléculas de glucosa en primer término aceptan grupos fósforo, convirtiéndose en la fructuosa-6-fosfato (F6P). Este último compuesto acepta nuevos grupos fosfato, reacción que se lleva a cabo en presencia de la enzima llamada fosfofructuocinasa (PFK), generándose el ADP y la fructuosa difosfato (FDP). Para atender mejor este asunto, que cada vez se complica más, presentamos la figura 34, en donde aparece un diagrama de la estructura de control del proceso glicolítico. Desde su descubrimiento en 1964 el ciclo ha sido el arquetipo de las reacciones oscilatorias en bioquímica; para su estudio se han empleado preparaciones de músculo cardiaco, extractos de células de hongos, etc. Las oscilaciones del ciclo se han puesto en evidencia al medir la concentración de la especie NADH y se sabe hoy en día, con un alto grado de confianza, que las variaciones cíclicas son una consecuencia de los famosos interruptores químicos que actúan en las enzimas. En particular la enzima PFK es alostérica, esto quiere decir que su estructura posee subunidades catalíticamente activas en las que se realizan reacciones diferentes. Cuando un sustrato llega a uno de esos sitios puede afectar la actividad de las subunidades, incrementando la producción de una determinada sustancia a costa de inhibir la generación de otras que se realizan en un sitio diferente. Para el caso que nos concierne se sabe que el ATP inhibe la enzima y que el ADP la activa. El ciclo glicolítico se ha presentado mediante el esquema de la reacción que ya vimos, y sus oscilaciones periódicas se han reproducido mediante la ayuda computacional. Los investigadores han modificado el modelo en la computadora haciendo variar la concentración inicial de glucosa: el caos se hizo presente en dichos modelos entre regiones de oscilaciones simples y otras más complejas. Bueno, dirá el lector, eso no es más que la simulación en computadora, pero no hay ejemplos autónomos de casos en sistemas bioquímicos. Para aclarar este punto pasemos a otro ejemplo que esperamos sea más convincente. En la figura 35 representamos en forma muy esquematizada el llamado ciclo del ácido cítrico, mejor conocido como ciclo de Krebs, en honor a Hans Krebs, bioquímico alemán nacido en 1900.
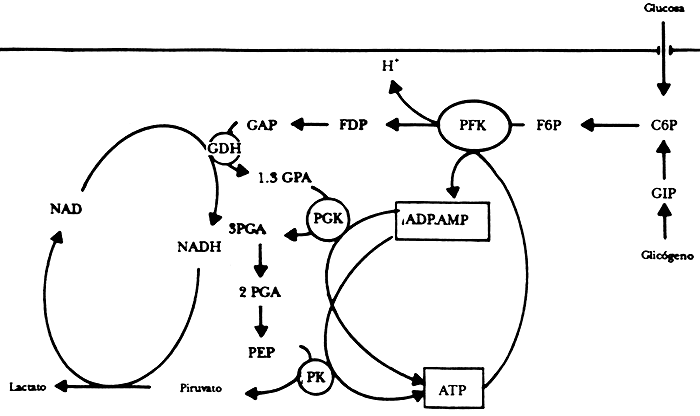
Figura 34. Esquema simplificado del ciclo glicolítico. C6P = glucosa - 6-fosfato, G1P = glucosa-1 - fosfato, F6P = fructuosa - 6 fosfato, PFK = fosfofructo - cinasa, FDP = fructuosa - disfosfato, GAP = fosfogliceraldehído PK = piruvato - cinasa, 2 PGA, 3 PGA y 1-3 PGA = fosfogliceraldehídos, PEP = fofoenol - piruvato.
El ciclo es uno de los mecanismos más importantes que tienen los organismos vivos, pues regula el metabolismo de los carbohidratos y de los ácidos grasos en las células, además de ser fundamental en los procesos biosintéticos. La reacción neta consiste en la oxidación completa de dos grupos carboxílicos (CH3COOH) en bióxido de carbono y agua. Durante el transcurso de la transformación se generan doce enlaces fosfato de alta energía, y algunos de ellos provienen de una reacción de oxidación de la especie nicotinamida-adenina dinucleótido (NADH), la cual interviene en varias partes del ciclo de Krebs, catalizada por una enzima llamada peroxidasa. Tomemos una lupa imaginaria e indaguemos en este vasto y complejo mecanismo donde intervienen otros reactivos y productos no incluidos en el esquema de la reacción de oxidación del NADH catalizada por la enzima peroxidasa. Un modelo sencillo de la reacción es el siguiente:
La reacción consiste en la oxidación del NADH con la consecuente reducción
del oxígeno molecular en presencia de un ácido, representado por la especie
H+. La enzima interviene en su forma oxidada y reducida, asociada
en ambos casos con el ion Fe (quizá el lector pueda de inmediato llegar a la
conclusión de que lo que estudiaba el biofisico Belousov en su laboratorio estaba
relacionado con el ciclo de Krebs, cuando encontró la peculiar reacción que
hemos visto). En 1965, muy poco tiempo después de haber sido descubierta la
reacción de Belousov, un grupo japonés encabezado por I. Yamazaki informó que
bajo ciertas condiciones experimentales, la concentración de oxígeno medido
presentaba oscilaciones periódicas. En otra parte del orbe, los daneses L. Olsen
y H. Degn emprendieron un largo proyecto de investigación para estudiar las
misteriosas oscilaciones de esta reacción bioquímica. Comprobaron que al disminuir
paulatinamente la cantidad inicial de enzima que se añadía a la reacción, había
un punto en donde era posible obtener un comportamiento caótico, como
lo llamaron en un artículo publicado en 1977. La investigación no quedó ahí;
se llegó a proponer un modelo cinético que, mediante simulación computacional,
era capaz de reproducir los resultados obtenidos en el laboratorio y, más aún,
dibujar el tipo de atractor extraño que se generaba. He aquí un modelo simplificado
del mecanismo de reacción:
| A + B + X |
® |
2X | (R1) |
| 2X |
® |
2Y | (R2) |
| A + B + Y |
® |
2X | (R3) |
| X |
® |
P | (R4) |
| Y |
® |
Q | (R5) |
En este caso, A representa la cantidad de oxígeno proveniente de la fase gaseosa
que se disuelve en la solución reaccionante, B representa la cantidad de NADH,
X y Yson especies intermedias que no aparecen en los productos finales, mientras
que P y Q son dichos productos. Hemos de aclarar que en la práctica se ha constatado
que la reacción tiene más de veinte pasos, muchos de ellos aún no conocidos
con suficiente detalle. El lector ya habrá observado que la dinámica de la reacción
no es tan sencilla como aparenta, por lo que en la figura 36 se presenta un
diagrama para aclarar el proceso. Note que las tres primeras reacciones son
autocatalíticas, y que en la primera y en la tercera se genera el mismo producto,
X, pero con reactivos diferentes en cada caso. Así encontramos dos subsistemas
que operan entrelazados a manera de interruptores químicos; por tanto es de
esperar que bajo ciertas circunstancias las oscilaciones actúen en forma sincronizada,
otras veces en forma alternada y lo más importante, que en algunas ocasiones
entren en un estado caótico.
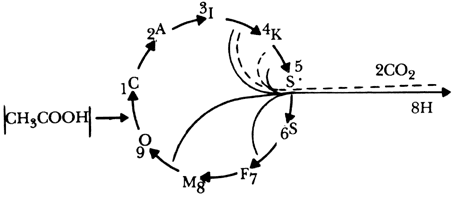
Figura 35. Diagrama simplificado del ciclo de Krebs. Los componentes principales son: C = citrato, A = cis-aconiato, I = isocianato, K = alfa cetoglutárico, S5 = succinil coenzima A, S6 = succinato, F = fumarato, M = malato, 0 = oxaloacetato. El acetato entra al ciclo como acetil coenzima A (paso 1 y reacciona con el oxaloacetato y agua para formar el citrato.
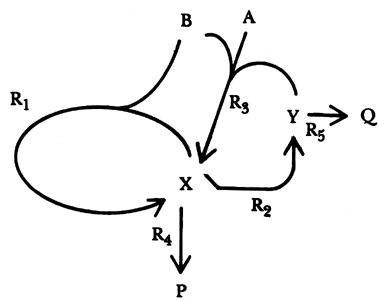
Figura 36. Esquema del ciclo de la oxidación de la NAHD catalizada por la perioxidasa.
En 1970, A. Zaikin y nuestro conocido A. Shabotinsky publicaron un artículo en el cual describían algunas peculiaridades de la reacción B-Z. Haciendo referencia a la propagación de las ondas producidas por las oscilaciones del sistema, decían que un modelo muy parecido debería aplicarse para explicar los impulsos de propagación en el músculo cardiaco. Una de las referencias que nos dan los autores es nada menos que un artículo aparecido en los archivos del Instituto de Cardiología de México, firmado por N. Weiner y A. Rosenblueth en 1946.
Podemos hacer una analogía entre la reacción química de B-Z y el músculo cardiaco imaginando que las "especies que se propagan" en el primer caso representan un potencial eléctrico para el segundo y que "el catalizador" está constituido por un conjunto de proteínas diseminadas en células especializadas. Las ecuaciones que gobiernan tal sistema, que incluyen la reacción y difusión, son diferenciales, como las que se aplican a las reacciones químicas que hemos descrito en el curso de este libro. Veamos entonces dónde entra el caos en el corazón.
Primero revisemos la forma en que trabaja. El corazón es un músculo cuya función es semejante a la de un motor; su contracción (sístole) alterna con periodos de reposo (diástole) y ese movimiento está gobernado por un sistema de "arranque" que asegura el funcionamiento automático de este sistema mecánico. Los datos electroquímicos asociados con el latido del corazón se registran mediante el electrocardiograma, inventado en 1903 por el fisiólogo holandés W. Einthoven, ganador del premio Nobel de medicina y fisiología en 1924. El principio es sencillo: la actividad de las células responsables del automatismo cardiaco se acompaña por fenómenos eléctricos característicos que se registran con la ayuda de electrodos dispuestos en la superficie del corazón. La contracción de las aurículas, que precede a la de los ventrículos es provocada por la activación automática y regular de un grupo de células anatómicamente diferentes de las células contráctiles situadas en la parte alta de la aurícula derecha. De ahí parte una corriente eléctrica que provoca la activación de las células vecinas de las dos aurículas, pero que es transmitida a los ventrículos al poco tiempo mediante otro grupo de células especializadas que forman una red que se disemina en los ventrículos, algo así como el "cable eléctrico" que permite la conexión entre las células especializadas en la conducción y las células cardiacas puramente contráctiles. La contracción está precedida por cambios eléctricos llamados despolarizaciones, que se registran mediante los electrodos. En el electrocardiograma se aprecia una primera onda que corresponde a la de polarización de las aurículas, seguida de una segunda provocada por la contracción de los ventrículos, y por último otra que proviene de la repolarización de los ventrículos.
L.Glass y colaboradores llevaron a cabo en Canadá un estudio experimental que ha revelado datos muy interesantes sobre el comportamiento de las células cardiacas. Los investigadores aislaron un grupo de este tipo de células en embriones de pollo, las cuales transferidas a un medio de cultivo apropiado, laten espontáneamente con un ritmo regular que se registra con la ayuda de diminutos electrodos. Estos últimos sirven también para enviar a las células pulsos de corriente en las diversas fases del ciclo espontáneo de latidos. Si se asume que la dinámica del movimiento del corazón puede ser representada por una ecuación diferencial que describe la evolución en el tiempo, la representación del oscilador cardiaco en un diagrama de fases describirá un atractor de ciclo limitado. Un estímulo eléctrico desplazará el oscilador hacia un nuevo punto en el espacio de fases, distancia que puede ser medida experimentalmente.
Glass y colaboradores observaron que al aplicarse un campo eléctrico fuerte, el latido siguiente ocurre más pronto o después de lo normal. Si se aplican impulsos periódicos el agregado celular se encuentra solicitado por dos fuerzas de periodos diferentes: uno con el ritmo intrínseco de las células cardiacas y el otro con el ritmo provocado por la corriente eléctrica aplicada externamente. El latido cardiaco que se produce dependerá de la relación existente entre los dos periodos. En ciertos casos las células laten una, dos o tres veces seguidas por cada dos impulsos externos, pero en otras circunstancias la contracción es aparentemente azarosa, produciendo formas irregulares, caóticas. Estas experiencias son interesantes porque muestran que se puede inducir caos en un sistema artificial que simula los procesos cardíacos. Además, cuando se comparan las dinámicas observadas en el experimento con las que detecta el electrocardiograma de pacientes cardiacos, existe una notable similitud. Glass ha llegado a la conclusión de que muchos problemas patológicos de los humanos son producto de lo que él ha dado en llamar enfermedades dinámicas. Este tipo de enfermedades, que es el caso de las cardiacas, resultan de cambios en las variables fisiológicas que normalmente se responsabilizan de los procesos rítmicos, las cuales de repente fluctúan de manera caótica. En el hombre adulto, el ritmo cardiaco normal es de 60 a 100 latidos por minuto. Hay dos grandes categorías de problemas rítmicos: por una parte está la aceleración de la frecuencia cardiaca, taquicardia, y por la otra la desaceleración del ritmo a menos de 60 latidos, que se conoce como braquicardia. Los síntomas de cualquiera de los dos tipos de enfermedades van desde la fatiga al esfuerzo, hasta la muerte súbita. En este último caso, es bien conocida la llamada fibrilación ventricular, que se manifiesta por una anarquía total de la contracción de las fibras musculares y que es antecedida por un ritmo cardiaco caótico generado por bifurcaciones periódicas como las que presenta la reacción de Belousov. Hay quien afirma, como es el caso de A. Goldberger de la Escuela de Medicina de Harvard, que el caos procura al cuerpo humano una flexibilidad que le permite responder a diferentes tipos de estímulos; para el caso específico del ritmo cardiaco afirma que en una persona normal éstos son caóticos. Su afirmación se basa en el análisis del espectro de frecuencia del electrocardiograma de personas sanas y pacientes cardiacos. Para el caso de los primeros, dice Goldberger, se presentan irregularidades que van desde algunos segundos hasta días, mientras que en los enfermos los espectros son más constantes. Como es común en las ciencias, hay quien refuta las observaciones del autor y afirma que no necesariamente existe el caos, ya que las irregularidades pueden ser señales que se reciben accidentalmente en el organismo en el momento en que se hacen los registros.
¿Tiene usted una respiración irregular? ¡Atribúyale la enfermedad al caos! Este padecimiento es otro de las llamadas enfermedades dinámicas. Le explicaremos su problema: usted tiene dificultad en el control de la eliminación del bióxido de carbono. Es posible analizar este padecimiento matemáticamente. Considere la ecuación diferencial: dX/dt=A - Bx, en la cual X es la variable de interés, t es el tiempo, y A y B son constantes positivas que representan la velocidad de producción y eliminación de la variable X. En muchos sistemas fisiológicos, A y B no son constantes sino que dependen del valor que tenía X en un tiempo previo. Por lo tanto, la velocidad instantanea de cambio de X respecto al tiempo es función de un valor X t-a. Si se aplica una ecuación de esta naturaleza al sistema de control fisiológico que nos ocupa, A representa la velocidad de producción del bióxido de carbono y en B quedan englobados factores como el tiempo transcurrido entre la oxigenación de la sangre en los pulmones y la estimulación de los receptores químicos por parte del cerebro. Al proveer de valores a la ecuación e iterarla para diversos tiempos se genera un diagrama en el que se grafica el volumen del bióxido de carbono expelido, el cual reproduce oscilaciones no periódicas en el proceso con las clásicas características de los fenómenos caóticos, como por ejemplo la sensibilidad a las condiciones iniciales. Por lo tanto, este modelo matemático sencillo de la circulación del bióxido de carbono en el curso del proceso respiratorio puede presentar un comportamiento irregular y caótico para ciertos valores de los criterios característicos de la biofísica del ciclo del bióxido, resultados que son comparables con los que se observan en ciertos pacientes que han sufrido accidentes cardiacos congestivos. M. Mackey y L. Glass, autores del trabajo anterior, sugieren que es muy importante profundizar en el conocimiento de los datos experimentales y clínicos que se poseen de los pacientes, para determinar si existen secuencias de bifurcaciones similares a las observadas en el modelo; además insisten en que es necesario diseñar nuevas estrategias terapéuticas basadas en la manipulación de los criterios de control identificados, para así resolver enteramente estos padecimientos a la mayor brevedad posible.
W. Freeman, profesor de neurobiología de la Universidad de California ha estudiado por más de 30 años los fenómenos de la percepción. Al ver, oír y escuchar, nuestro cerebro desencadena en fracción de segundos un mecanismo complejo por el cual reconocemos el estímulo que lo provoca. La percepción, nos dice el autor, no puede comprenderse examinando únicamente las propiedades microscópicas de las neuronas en forma individual, se debe entender que se trata de la acción cooperativa de millones de neuronas que están localizadas en diferentes puntos de la corteza cerebral. El caos determinista, según Freeman, está presente en esos mecanismos complejos, ya que representa una forma de entender cómo un grupo de neuronas cambia abruptamente la actividad que realiza al menor estímulo. Se adentra en el terreno de la especulación y propone que gracias al caos es posible que el cerebro sea flexible en su respuesta al mundo exterior y más aún, que sea capaz de generar nuevos modelos de actividad. Alejémonos de la especulación y veamos cuáles son los trabajos de Freeman que lo han llevado a tales afirmaciones. El científico ha dedicado mucho esfuerzo para comprender cómo funcionan las neuronas del sistema olfatorio; veamos lo que se conoce al respecto.
Cuando se huele un aroma las moléculas que lo provocan son capturadas por una pequeña porción del inmenso número de receptores neuronales que se encuentran ubicados en la nariz. De alguna manera, cada receptor está especializado para responder a un tipo de aroma en particular. El estímulo genera en las células una serie de pulsos que se propaga vía los axones hasta el llamado bulbo olfatorio; aquí se analizan los estímulos recibidos y se transcriben en un nuevo mensaje que es transmitido por los axones hacia la corteza olfatoria; ésta se encarga de enviarlo a muchas partes del cerebro que mezclan dichas señales con las provenientes de otros sistemas sensoriales. El resultado de todo este proceso es la percepción de un aroma que es único para cada individuo. Experimentalmente, Freeman y sus colaboradores entrenan a un grupo de animales para que respondan al estimulo de varios aromas, en cada caso se enseña al animal a que se comporte de una manera particular ante un aroma en particular. En "recompensa" al aprendizaje se le colocan 65 electrodos en gran parte de la superficie bulbar, con los que pueden obtener simultáneamente otros tantos electroencefalogramas (EEG) que miden la actividad neuronal. El registro de los EEG para la región del bulbo olfatorio y la corteza olfatoria muestra ondas de baja frecuencia que se ven interrumpidas por oscilaciones de gran amplitud y alta frecuencia cuando el animal percibe el olor. Estas oscilaciones duran una fracción de segundo en el intervalo entre la inhalación y exhalación. Como dato curioso debemos apuntar que este mismo modelo de oscilaciones se encuentra en la reacción de Belousov-Shabotinsky cuando la experiencia se realiza en un sistema abierto. Estos sobresaltos oscilatorios representan una actividad cooperativa del sistema neuronal del cual se puede obtener un mapa donde se grafican las amplitudes por medio de cada uno de los electrodos. El mapa revela un diagrama de contornos con elevaciones de valles y montañas que se repite cuando el animal vuelve a inhalar un aroma en particular. Hay muchas razones para creer que la actividad del cerebro durante los sobresaltos, y en los espacios de tiempo entre ellos, es caótica y no simplemente azarosa. La diferencia entre estos dos estados es similar a la que existe entre la gente que transita por una estación de correspondencia del Metro y una multitud aterrorizada.
En el primer caso, aunque la gente pasa corriendo para tomar un determinado tren, en el proceso hay un orden oculto y el flujo de movimiento puede cambiarse si se ordena por el altoparlante un cambio en la dirección de los trenes. En el caso de la multitud en pánico un anuncio no cambiará nada la situación y la cooperación no hará acto de presencia.
Entre las aparentes evidencias de que el fenómeno es caótico podemos mencionar el que el conjunto neuronal del bulbo y la corteza pasan al unísono e instantáneamente de periodos de sobresaltos a otros de aparente calma, para reincidir de nuevo en las oscilaciones, comportamiento que es propio de los estados caóticos que en física llamamos transiciones de fase, y bifurcaciones en matemáticas. Más evidencia se suma a los hechos cuando los autores desarrollan y aplican un modelo computacional del sistema olfatorio en su totalidad. Mediante esta herramienta se simula la actividad del sistema resolviendo un conjunto de ecuaciones diferenciales que "describen" la dinámica de las neuronas. El modelo, ante el estímulo de un simple pulso (equivalente a la excitación de unas cuantas neuronas) es capaz de reproducir una actividad semejante a la que se observa en los EEG. A partir de esta simulación se representan los resultados de la actividad mediante un diagrama de fases en donde se grafican las amplitudes en función del tiempo (en este caso a cada milésima de segundo de intervalo). El resultado es un atractor extraño. Los científicos piensan que el caos en el cerebro es consecuencia de que dos áreas, en este caso el bulbo y la corteza, se excitan una a otra pero no son capaces de generar una frecuencia común de oscilación. La competencia entre las partes incrementa la sensibilidad e inestabilidad del sistema, que contribuyen al caos, afirmación que se confirma cuando se interrumpe la conexión entre el bulbo y la corteza, ya que el caos desaparece.
Entre los científicos, en particular en aquellos dedicados al estudio de la evolución, existen dos posturas respecto al papel que pueden desempeñar las dinámicas caóticas en los seres vivos. Hay quienes categóricamente afirman que éstas no existen en las poblaciones reales y añaden que de existir fluctuaciones caóticas se crearía un riesgo intrínseco en la evolución que ocasionaría la extinción progresiva de dicha especie. M. Conrad, especialista en biología y las ciencias de la computación de la Universidad de Wayne, Estados Unidos, tiene una visión diferente. Hemos visto que muchos modelos dinámicos de los complejos sistemas biológicos llegan a ser caóticos si se escogen ciertos valores para los criterios que los controlan. Los resultados caóticos de estas ecuaciones son semejantes a los obtenidos en reacciones químicas inorgánicas como la de Belousov-Shabotinsky. ¿Cuál es entonces la función que tiene una dinámica caótica en un organismo vivo? Conrad nos lo explica de la siguiente manera: la posibilidad de interpretar el caos biológico en términos funcionales está basada en el hecho de que cualquier sistema de este tipo debe ingeniárselas para permanecer en el juego de la vida. Para ello es necesario que la dinámica de las partes que lo conforman sea consistente con la dinámica del conjunto y ésta a su vez sea consistente con sus partes. El más importante mecanismo para alcanzar tal autoconsistencia es la selección natural. Si la dinámica de un organismo individual no es congruente con la estabilidad del ecosistema como un todo, será inevitable que la selección natural lo elimine. En su evolución hacia estados que le permitan seguir funcionando, Conrad nos dice cuáles son las posibles funciones que puede tener el caos; revisémoslas brevemente:
1) Búsqueda de nuevos procesos. En esta categoría se genera y se ponen a prueba un conjunto de posibilidades nuevas. Entre ellas, la más importante sería la diversificación genética a través de la mutación y otras operaciones genéticas. Con ello se crearían nuevos genotipos sobre los cuales actuaría la selección natural. Aún no hay evidencia directa de que las dinámicas caóticas actúen directamente en el nivel genético.
2) Defensa. Los mecanismos caóticos pueden ser empleados para evadir a los predadores. Por ejemplo, un animal que se mueve de manera azarosa (por ejemplo mariposa) es más difícil de atrapar que aquel que posee movimientos predecibles. En este caso se podría pensar que el caos está instalado en el nivel neuronal.
3) Previene al sistema biológico de la "burocracia". En ausencia del caos, la actividad del sistema se anquilosaría de tal manera que le sería difícil responder en forma dinámica a un estímulo que la acecha. El éxito de la adaptabilidad será más eficiente en un sistema cuyas partes están más descentralizadas, más independientes. Piense el lector en el sistema inmunológico; la gran diversidad de moléculas de inmunoglobulina hace posible que el organismo pueda luchar con un mundo microbiano muy diverso.
El descubrimiento del caos determinista en muchas áreas de la ciencia y en especial aquellas relacionadas con la química de los seres vivos, ha motivado en los científicos nuevas reflexiones que intentaremos resumir en este apartado. Es obvio que todos los sistemas vivientes son estructuras muy bien ordenadas que permanecen en el juego de la vida gracias al equilibrio preciso entre la actividad química y el comportamiento. Hay quienes piensan, como S. Kauffman, profesor de bioquímica y biofisica de la Universidad de Pennsylvania, que es posible que el orden biológico sea un reflejo parcial del orden espontáneo sobre el cual actúa la selección natural. Esta moldea la coherencia propia del desarrollo biológico, y es la evolución la que aporta la capacidad para cambiar y adaptarse. Una nueva vertiente, tentativa e incompleta, nos dice Kauffman, emerge en ese sentido: la evolución se comprende como la sumatoria de la selección y la autoorganización, esta última es una propiedad innata de algunos sistemas complejos. Los sistemas complejos presentan fenómenos como el caos determinista, pero también, dice el autor, podemos pensar en el anticaos, un sistema desordenado que "cristaliza" en orden. ¿Cómo funciona la lógica y estructura de un sistema regulatorio, como sería el caso del genoma de un ser humano con capacidad para formar 100 000 diferentes proteínas? Para estudiar el problema se crean modelos matemáticos que describen cómo los elementos individuales del sistema se conectan y regulan mutuamente mediante funciones lógicas. Cada combinación de funciones que se genera constituye un nuevo estado del sistema y la sucesión de estados es la trayectoria que sigue el sistema. El modelo presupone que existe un número finito de estados y que a la larga el sistema volverá a un estado anterior: esto se llama un atractor dinámico. Mediante la simulación se ha demostrado que para un sistema constituido por N elementos, en el que cada uno puede ser modificado en su comportamiento por tres posibles señales, S, el nuevo estado del sistema tiene un comportamiento caótico, hay sensibilidad a las condiciones iniciales, y si el número de elementos crece el tamaño del ciclo también, pero exponencialmente. Sin embargo, cuando S=2, las propiedades caóticas desaparecen abruptamente y el sistema exhibe un orden colectivo espontáneo y los atractores resisten, por así decirlo, a mínimas perturbaciones. ¿Por qué un sistema que tiene únicamente dos señales por cada elemento exhibe tal orden? La respuesta no es fácil; los especialistas que estudian los mecanismos de transmisión de señales en un sistema conectado entre si nos indican que en el vasto enrejado interconectado se forman cúmulos de elementos que se encierran en sí mismos como islas que permanecen funcionando en forma aislada y no pueden propagarse; el sistema en su totalidad se ordena porque los cambios en su comportamiento son pequeños y aislados.
Si cada uno de los 100 000 elementos que posee el genoma humano recibiera dos señales, potencialmente podría asumir 10 30 000 diferentes estados. Sin embargo, el sistema asume un orden tal que el número de ciclos calculados no pasa de 370 estados. Si uno supone que cada tipo de célula es en sí un atractor, deberia ser posible predecir cuántos tipos de células aparecen en el organismo. El número de atractores es aproximadamente igual a la raíz cuadrada del número de elementos en el sistema, por tanto, el número de tipos de células debería ser casi igual a la raíz cuadrada del número de genes. Si se asume que ese número es proporcional a la cantidad de ADN en una célula, entonces los humanos tendrían aproximadamente 100 000 genes y 370 variedades de células. La cuenta más reciente en los humanos distingue 254 tipos, la predicción del modelo no está muy alejada de la realidad. Otra predicción de este tipo de modelos se refiere a la estabilidad de los diferentes tipos de células. Si cada célula es un atractor, entonces no puede ser fácilmente alterada por cualquier perturbación, ya que su estabilidad es una propiedad que emerge el sistema regulatorio que tienen los genes, hipótesis de la evolución que está gobernada por sistemas regulatorios que funcionan en el límite entre el orden y el caos.