II. NUEVAS REGLAS, NUEVAS GEOMETRÍAS

NUESTRO mundo está constituido por montañas, costas, mares, nubes, plantas, animales, etc.; sin duda alguna es el reino de la forma. Si quisiéramos describirlo, un vistazo rápido podría desalentar todo intento de realizar simplificaciones; más que el reflejo de la perfecta armonía de un mundo sencillo y ordenado, parece ser el dominio de la irregularidad y el caos.

Cuerpos amorfos desde rocas hasta planetas, flujos turbulentos desde ríos a tornados, patrones asimétricos que sobrepasan con mucho el número de cuerpos regulares con los que el hombre se ha obsesionado desde el inicio de los tiempos. Azar y desorden en un Universo aparentemente estructurado.

Sin embargo, en este mar de caos, una observación más cuidadosa de la naturaleza muestra que aun dentro de su enorme complejidad existen ciertos patrones que la caracterizan.

Una roca es similar a la montaña de la que forma parte; una rama tiene la misma estructura que la del tronco del que nace; como si la decisión hubiera sido repetir la misma forma a diferentes escalas dentro de un mismo objeto, asegurando la preservación de una copia del original a cualquier nivel de amplificación; como si se pensara en generar el máximo nivel de detalle con el mínimo costo en el diseño.

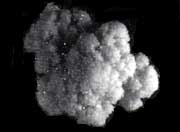
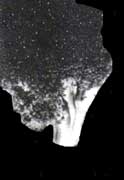
Un helecho cuerno de ciervo (Figura 1), un brócoli o una coliflor (Figura 2) son muestras vivas de este juego de la naturaleza en el que el mismo patrón de crecimiento se manifiesta a diferentes escalas, y aunque es verdad que la realidad pone límites a la imaginación, nada nos impide especular sobre las propiedades de helechos "imaginarios" que aun a nivel microscópico exhiban características geométricas semejantes a las de la planta completa. Objetos que en sus detalles se repiten a sí mismos, siguiendo una idea semejante a la plasmada en las famosas muñecas de los artesanos rusos.

 

 

 

Figura 1. Fotografía de un helecho cuerno de ciervo. La repetición del mismo patrón de crecimineto se presenta a varias escalas. (Fotos: Guillermo Sosa.)

 

 

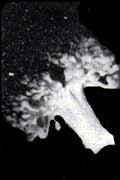Figura 2. Los diferentes pedazos de la coliflor tienen una estructura muy similar a la de la cabeza completa. Con el brócoli sucede lo mismo. (Fotos: Guillermo Sosa).

Estructuras como éstas se conocen desde hace mucho tiempo en el campo de las matemáticas. Quizá uno de los ejemplos más representativos sea la curva construida por la matemática sueca Helge von Koch en 1904 (Peterson, 1988). Para dibujarla basta tomar un triángulo equilátero como figura inicial (Figura 3(a)) y añadir en el centro de cada uno de sus lados un nuevo triángulo equilátero tres veces más pequeño que el original (Figura 3(b)). Repitiendo indefinidamente este proceso (Figura 3(c) y 3(d)) se obtiene la curva o copo de nieve de Koch.

Figura 3. Éstas son las primeras cuatro etapas del proceso de iteración que da lugar a la curva de Koch.

Triángulo sobre triángulo hasta el límite de cualquier imaginación, la curva así construida resulta indibujable, pues la forma del contorno se repite a todos los niveles. Cada punto sobre ella, si lo exploráramos con una lupa, nos revelaría siempre los mismos secretos; triángulo sobre triángulo, indefinidamente.

A entidades como ésta se les denomina autosimilares, pues cada una de sus partes es igual al total (su apariencia es la misma a cualquier escala) y desde el punto de vista matemático poseen ciertas propiedades peculiares que las distinguen (Briggs, 1990).

LA PATOLOGÍA DE LO QUE LLAMAREMOS FRACTALES

¿Cuál es la longitud de la curva de Koch? Es claro que la respuesta depende del tipo de regla que se utilice para medirla. Si nuestro instrumento de medida es poco flexible y sus divisiones no son muy finas, el valor obtenido será inexacto y sólo un burdo reflejo de la extensión de la curva real. La regla no puede penetrar y considerar todos los detalles de la figura.

Si para delinear mejor las sinuosidades de la ruta decidiéramos recorrer la curva ajustando un hilo sobre su perímetro, un momento de reflexión nos permitiría ver que la presencia de detalle a toda escala hace imposible nuestra tarea si no contamos con un filamento inmensamente largo; sólo así podríamos visitar todos los recovecos del contorno. La curva es generada en un proceso de repetición que añade más y más detalle a cada paso, extendiendo su longitud sin límite alguno. Si la cortamos en un punto y la estiramos, podemos generar con ella una recta de longitud infinita, pensemos que siempre habrá un pico que desdoblar, y dentro de éste otro, y luego otro, y otro, y así hasta el cansancio.

El resultado es sorprendente; nos encontramos con un objeto que a pesar de estar definido sobre una región finita del espacio posee una frontera de extensión ilimitada. La curva de Koch envuelve un área que no es mucho mayor que la que tiene el primer triángulo del que se parte, de hecho, se puede demostrar que es sólo 1.6 veces más grande.

El contorno del copo de nieve de Koch es tan irregular que entre dos puntos cualquiera sobre él existe una distancia infinita y un número incontable de quiebres y zigzags. Esto último hace que sea imposible dibujar una tangente (recta que toque, sin cortar, a la curva en un solo punto) en algún lugar a lo largo de su perímetro. En esta curva, todo punto es un punto de quiebre al que no se puede ajustar una recta tangente con inclinación única (Figura 4(a)); esto la distingue de las curvas suaves con las que estamos más acostumbrados a tratar, en las que en cada punto se puede hacer pasar una tangente (Figura 4(b)); sólo para caracterizar este hecho diremos que la curva no es diferenciable.

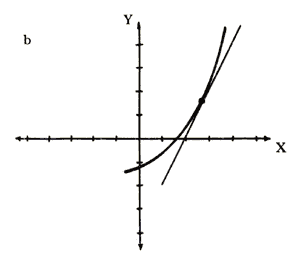
Figura 4. (a) En una curva como ésta no es posible asociar una tangente única a los puntos de quiebre y el copo de nieve de Koch los tiene en todas partes. (b) En una curva suave, a cada punto le corresponde una tangente con inclinación bien definida.

Las propiedades particulares de "monstruos" matemáticos como éste hacen que sea difícil establecer un mecanismo sistemático para compararlos y clasificarlos (Gardner, 1976); si tienen una longitud infinita, ¿cómo distinguirlos? El primer intento para lograrlo se basa en las ideas del matemático alemán Félix Hausdorff, quien en 1919 introdujo el concepto de dimensión que hoy permite caracterizarlos (Gould, 1988).

Establecer la dimensión de un objeto regular "a ojo" parece ser cosa fácil y requiere tan sólo de un poco de sentido común. Así decimos que un trozo de hilo es aproximadamente unidimensional y que una hoja de papel es un buen ejemplo de una forma en dos dimensiones. Sin embargo, si se nos pide definir un mecanismo práctico para verificarlo nos encontraremos en aprietos. Además, ¿es lo mismo una hoja lisa que una arrugada?; si el hilo es de longitud infinita, ¿no podríamos cubrir con él todo el plano? En fin, es mejor intentar generar un método que nos permita obtener respuestas sin dejar lugar a las dudas.

Tomemos primero el hilo, el cual representaremos como una recta de longitud L= 1 m , por ejemplo, y dividámoslo en tres pedazos iguales de l = 1/3 m de extensión. En este caso, el número de particiones que se generan (N) se obtiene determinando cuántas veces cabe una parte l en el total L: N = L/l = (L/l)¹=3:

Si repetimos este proceso sobre la hoja de papel a la que consideraremos como un cuadrado de lado L= 1 m, al que seccionamos en cuadrados más pequeños de lado l = l/2m y área l²=1/4 m², el número de particiones resulta ahora N=L²/l² = (L/l)²=4:

La extensión directa de los resultados anteriores al caso tridimensional nos llevaría a suponer que aquí debe cumplirse que N= (L/l)³ (parece que basta elevar L/l a una potencia igual a la dimensión de la figura), lo que se verifica con el cubo que dibujamos a continuación:

Al dividir cada lado a la mitad, l= L/2, se generan N=L³/l³=8 pequeños cubos de volumen l³.

Si generalizamos las relaciones obtenidas podemos decir que en un proceso de división como el descrito, el número de secciones generadas está dado por N=(L/l)d_f, donde d_f es lo que denominaremos la dimensión de Hausdorff del objeto; hay que notar que la misma relación debe cumplirse tanto si decidimos seccionar el objeto total como cualquiera de sus partes.

Encontramos así una estrategia para cuantificar la dimensión de cualquier forma geométrica, pues si N= (L/l)d_f, despejando:

d_f = log(N)/log(L/l)

Por ejemplo, al tomar un triángulo equilátero de lado L=1 y dividirlo en secciones de la mitad de extensión (l=1/2; L/l=2):

se obtienen cuatro particiones idénticas (N=4); de donde se deduce que como d_f =log(4)/log(2)=2, tratamos con un objeto bidimensional.

Apliquemos entonces nuestro resultado a la curva de Koch. En este caso, y a toda escala sobre la figura, una recta de longitud L es dividida en secciones de un tercio de extensión, l =L/3, y en el proceso se generan cuatro particiones de tamaño similar (N=4, pues generamos un pico):

Así tenemos d_f = log(4)/log(3)= 1.2619, ñun objeto con dimensión fraccional! El resultado es desconcertante pero indiscutible, y es una evidencia más de la singularidad de la forma geométrica que estudiamos. La dimensión de Hausdorff definida de esta manera es una medida de la complejidad y rugosidad del cuerpo, y nos da una idea de su extensión real en el espacio. El copo de nieve de Koch cubre más espacio que una recta (d_f=1), pero mucho menos que un plano (d_f=2).

Otros "monstruos" como la curva de Koch exhiben dimensiones fraccionales distintas y cada uno de ellos tiene una dimensión de Hausdorff que lo caracteriza. Tal es el caso, por ejemplo, de las figuras de Sierpinski (Figura 5).

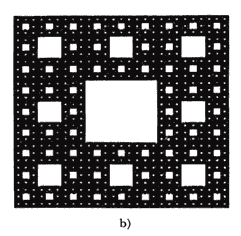
Figura 5. (a) Triángulo y (b) carpeta de Sierpinski.

El triángulo de Sierpinski es el resultado de seccionar a toda escala un triángulo equilátero en cuatro particiones similares cuyos lados son tan sólo la mitad de los de la figura original (L/l=2). Una vez hecho esto se extrae la sección central, de forma que queden las tres partes de los vértices (N=3), y sobre éstas se actúa de la misma manera:

Este proceso se repite en cada una de las partes restantes y así se procede ad infinitum; el resultado es similar al que aparece en la figura 5(a), aunque no hay pluma que permita dibujar la estructura con todo detalle. La dimensión de Hausdorff de la figura se obtiene considerando que cada vez que la longitud del triángulo se reduce a la mitad, aparecen tres triángulos más, por tanto, ñd_f =log(3) /log(2) =1.584!

De forma análoga puede construirse la carpeta de la figura 5(b) si la iteración (repetición de la misma operación o transformación a toda escala) consiste en dividir a todos los niveles un cuadrado en secciones de un noveno de área (L/l=3), eliminando la participación del centro:

Finalmente se tiene una forma geométrica cuya dimensión también es fraccional: d_f =log(8) /log (3) =1.893.

Comparando los resultados obtenidos para las tres figuras estudiadas se hace evidente que la dimensión de Hausdorff cuantifica hasta qué punto el objeto cubre el espacio en el que se encuentra inscrito: mientras la curva de Koch malcubre el plano d_f =1.263, la carpeta de Sierpinski, d_f =1.893, lo logra casi completamente. También hay formas de quedarse a la mitad del camino, ¿podríamos imaginar la estructura final que se obtendría de seguir reproduciendo a toda escala la greca de la figura siguiente? ¿Cuál sería la dimensión del objeto generado?

¿Y qué decir de la figura 6? ¿Podríamos identificar la operación que fue repetida varias veces sobre el cuadrado que sirvió de base?

Figura 6. ¿Qué dimensión tiene este fractal? ¿Cómo la obtenemos?

Si este esquema, de repetir el mismo patrón en todas partes dentro de una figura, se extiende a objetos definidos en el espacio de tres dimensiones, es claro que el número de "monstruos" que se pueden construir resulta ilimitado. Ahora bien, ¿tiene todo esto algo que ver con la realidad del mundo que nos rodea?

FRACTALES EN TODAS PARTES

En 1975 Benoit Mandelbrot denominó fractates (del latín fractus, irregular) al conjunto de formas que, generadas normalmente por un proceso de repetición, se caracterizan por poseer detalle a toda escala, por tener longitud infinita, por no ser diferenciables y por exhibir dimensión fraccional. Adicionalmente, construyó con ellas un conjunto de nuevas reglas para explorar la geometría de la naturaleza, y las reconoció como herramientas potencialmente útiles para analizar un gran número de fenómenos físicos (Peitgen, 1986).

El interés de Mandelbrot en los fractales nació de su certeza de que "las nubes no son esferas, las montañas no son conos, las costas no son círculos, como la corteza de un árbol no es plana ni un rayo viaja en línea recta... La naturaleza no solamente exhibe un grado mayor sino también un nivel diferente de complejidad" (Mandelbrot, 1984).

Hoy día se han identificado innumerables manifestaciones naturales de estructuras fractales. Se sabe que su geometría está presente en depósitos y agregados coloidales (como los generados por el polvo y el esmog), poliméricos y electroquímicos (Sander, 1987); en aparatos y sistemas de los seres vivos, como los vasos capilares, tubos intestinales, biliares y bronquiales, y en las redes neuronales (Goldberger, 1990). De manera similar, hay evidencia de que la localización geográfica de epicentros en temblores exhibe un patrón fractal (Bak, 1991), y en la actualidad la dimensión fraccional (dimensión fractal) de la superficie irregular de una falla en un material ya se utiliza como medida indirecta de su resistencia y dureza (Peterson, 1988).

Los fractales mostraron su utilidad por primera vez cuando se generó con ellos un modelo simple para la aprición de ruido en ciertas líneas de transmisión en sistemas de comunicación digital (Peterson, 1988); esto es, la presencia de breves interrupciones eléctricas que confunden y dificultan la comunicación (del tipo de las que estamos acostumbrados a oír cuando hablamos por teléfono o escuchamos el radio). El análisis de las señales demostró que las interrupciones aparecían como por paquetes, pero dentro de estos paquetes se distinguía una estructura intermitente, y dentro de ésta... ya podemos imaginar la historia. Un registro gráfico de las interrupciones dio lugar a un patrón fractal similar al que se obtiene a través del siguiente procedimiento. Tomamos una recta de longitud L y la seccionamos en tres partes idénticas (l=L/3), extrayendo después la sección central (nos queda N=2):

Cuando el procedimiento se repite a toda escala;

se obtiene el fractal conocido como conjunto de Cantor (Peitgen, 1992) en honor a su creador, el matemático alemán Georg Cantor; famoso por su desarrollo de la teoría de conjuntos. Este "monstruo" fue presentado al público por primera vez en 1883, y cien años después decidió aparecer por todas partes.

El conjunto o polvo de Cantor tiene una dimensión de Hausdorff menor que la unidad, pues cada vez que la longitud de un segmento se reduce a su tercera parte, sólo aparecen dos trozos más, d_f =log(N)/log(L/l)= log(2)/log(3)= 0.6309. En otras palabras, ñes más que una colección de puntos, pero menos que una línea! Es uno de los fractales más famosos, a pesar de no ser tan atractivo visualmente. Su estructura está detrás de varias cosas en el mundo real y así se ha utilizado como modelo para representar desde la distribución nada homogénea de los anillos de Saturno (Davies, 1987) y las fluctuaciones en el precio del algodón a partir del siglo pasado, hasta las variaciones que el nivel de las aguas del río Nilo ha experimentado desde hace 2 000 años. Más aún, cuando la idea que subyace en la construcción de este conjunto se extiende a tres dimensiones, el patrón que se genera coincide sorprendentemente con la distribución de estrellas y galaxias en el universo. Esto es más que suficiente como para quedarse anonadado.

En general, parece ser que dondequiera que un proceso irregular y caótico ha dado forma al ambiente (erosión acuosa y atmosférica, vientos, fallas geológicas) se han generado geometrías fractales (costas, ríos, montañas, nubes, rocas) que por su redundancia y falta de regularidad poseen propiedades estructurales particulares.

Así, para los geógrafos modernos, preguntas como "¿qué tan larga es la costa de Inglaterra?" Comienzan a carecer de sentido; pues ¿qué tan larga? depende de la escala y el detalle con el que se mida. Si se le cuantifica a partir de la información contenida en un globo terráqueo, un mapa de Europa, o una carta de navegación de la Gran Bretaña, la respuesta será distinta. ¿Cuál será la longitud para un viajero que decida recorrer todos los cabos y bahías? Para efectos prácticos, ilimitada. El problema es muy similar al que encontramos al intentar determinar la longitud de la curva de Koch; de hecho, fractales como éste resultan modelos más adecuados para representar el perfil de la costa que el trazo de una línea zigzagueante. En particular se ha calculado que la dimensión de Hausdorff de las costas terrestres se encuentra entre ñ1.15 y 1.35!; de nuevo entre la línea y el plano, pero ni una ni otro.

Es importante señalar que los fractales que existen en la naturaleza tienden a ser irregulares y son autosimilares sólo en sentido estadístico; esto es, si tomamos un conjunto suficientemente grande de objetos de la misma clase y amplificamos una porción de alguno de ellos, es posible que no sea idéntico al original, pero seguramente sí será similar a algún otro miembro de la colección. Su dimensión es fraccional pero se obtiene realizando promedios sobre sus valores en muchas regiones y para muchos cuerpos del mismo tipo. Cuando se amplifica una de las partes de un fractal natural, la propiedad de generar la misma figura, o alguna similar, tiene límites inferiores y superiores. Por ejemplo, al observar el perfil de una montaña, el tamaño de los objetos más grandes está determinado por la fuerza de gravedad, mientras que la menor escala de observación a la cual todavía se detectan los mismos detalles depende de la acción de la erosión y, por supuesto, del tamaño de los átomos. Los fractales son, en ese sentido, sólo una buena aproximación de la estructura de las formas naturales.

El mundo de los fractales está en pleno desarrollo en la actualidad. Así como la naturaleza parece haberlos elegido para generar formas complejas y únicas a través de un mecanismo de repetición muy simple, los seres humanos se sirven de ellos para almacenar y reproducir imágenes (Dewdney, 1990; Jñrgens, 1990), hacer modelos teóricos y experimentales de cuerpos irregulares (Peterson, 1988), analizar las características de pulsos cardiacos y nerviosos (Goldberger; 1990), desenmarañar la estructura de procesos dinámicos caóticos (Ford, 1989; Rietman, 1989), etcétera.

Para construir un fractal pueden seguirse procedimientos matemáticos, geométricos, físicos y químicos, y vale la pena dedicar un poco de tiempo a analizar los principios en que se basa cada uno de ellos. El interés de generar objetos fractales, como ya hemos visto, es muy diverso: representar imágenes, hacer modelos, analizar patrones, identificar estructuras. Pero este trabajo no es sólo un asunto de curiosidad científica o utilidad práctica inmediata; en él se esconde mucho de placer y de sorpresa, dos elementos que, como se verá, son inevitables.