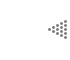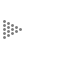III. EN EL PAÍS DE LAS MARAVILLAS

CUANDO Benoit Mandelbrot publicó en 1975 su primer ensayo sobre fractales no se atrevió realmente a dar una definición matemática formal que caracterizara a estos objetos; decidió simplemente utilizar el término para denominar las formas que compartían la característica común de ser a la vez rugosas y autosimilares. Mandelbrot buscaba otorgarles una categoría intermedia entre los cuerpos euclidianos regulares y lisos que nos son comunes (círculo, triángulo, esfera, etcétera), y las figuras que hoy día se denominan geométricamente caóticas y cuya apariencia es rugosa, pero sin exhibir ningún patrón geométrico regular.

Hacia 1977, el matemático se vio forzado a dar una definición formal que permitiera distinguir con más claridad una entidad fractal. Para hacerlo recurrió al antiguo concepto de dimensión de Hausdorff y en respuesta al pragmatismo definió, en general, todos los fractales como el conjunto de formas con dimensión fraccional. Mandelbrot era perfectamente consciente de que esta definición, si bien establecía una frontera bien delimitada con la geometría euclidiana de los conos y las esferas (en la que los cuerpos tienen una dimensión de Hausdorff entera), dejaba una puerta abierta hacia la región del caos geométrico. Sin embargo, a la espera de mejores definiciones, inició el trabajo que con hechos y con el lenguaje de las imágenes le mostraría al mundo el verdadero significado del término fractal. Sus resultados abrieron la puerta de un mundo impresionante donde habita el verdadero sentido de la palabra obsesión, donde las matemáticas se confunden con el arte, y la ciencia ha encontrado nuevas respuestas. Veamos en qué consistió su juego.

DE BÚSQUEDAS E ITERACIONES

A finales de los años setenta Benoit Mandelbrot incursionó en un área de las matemáticas que lo llevó a construir algunos de los objetos geométricos más complejos y hermosos que se conocen. Lo increíble es que el procedimiento que utilizó para hacerlo es muy sencillo: sólo hay que repetir y repetir una operación un sinnúmero de veces.

La idea se basa en tomar un número sobre el que se hace una operación, repetir lo mismo con el resultado y continuar haciéndolo indefinidamente en los siguientes resultados obtenidos. Formalmente se dice que se hace una iteración y se representa de manera general como:

x_n+1=f(x_n).

Para comprenderlo mejor, imaginemos que la operación por repetir consiste en elevar un número al cuadrado. Entonces la iteración se simbolizaría así:

x_n+1=x²_n

Al aplicarla sobre un valor inicial cualquiera, por ejemplo, x_o=2, el primer cálculo nos daría x₁=(2)²=4; después x₂=(4)² =16, y x₃=(16)²=256, y así seguimos. La secuencia de números que se genera:

2ñ 4ñ 16ñ 256ñ 65536ñ ...ñ ñ

se denomina la órbita de la iteración, y el punto al que se tiende a llegar (infinito, ñ, en este caso) se le llama su atractor. Si el valor inicial elegido es distinto, x=0.5, por ejemplo, la órbita será:

0.5ñ 0.25ñ 0.0625ñ 0.00390625ñ ...ñ 0,

y el atractor es el número 0.

Si x₀=1, las cosas son un poco distintas, pues el resultado siempre es 1, y no hay manera de salir de ahí; la órbita está constituida por un solo punto al que se le llama punto fijo. En la iteración que escogimos, los números x=0 y xñ ñ también son puntos fijos, pues al elevarlos al cuadrado no producen ningún resultado distinto.

Al trabajar con una iteración resulta interesante estudiar las características de las órbitas, atractores y puntos fijos que se obtienen después de hacer las operaciones sobre un gran conjunto de puntos. Aquí es donde está la segunda parte del problema, pues una vez elegida la operación, hay que decidir con qué tipo de números trabajar: ¿los enteros positivos?, ¿todos los números de la recta numérica (a los que llamamos números reales)? Las posibilidades son muchas, pero Mandelbrot seleccionó a los denominados números complejos.

ALGO SOBRE NÚMEROS COMPLEJOS

Los números reales constituyen una manera de etiquetar cada punto situado sobre la recta numérica de forma única e inequívoca; el 1 está antes que el 2, y el 1.5 se localiza entre ellos; a cada número le corresponde un punto y cada punto tiene su etiqueta numérica. Hay reglas para sumarlos y multiplicarlos que todos conocemos bien: 2 + 2 = 4, 3 x 4 = 12, etcétera.

Los números complejos funcionan de manera similar, ya que también permiten caracterizar puntos, pero éstos no están sobre una línea, sino sobre un plano al que llamamos plano complejo.

Todo número complejo, al que siempre simbolizaremos con la letra z, consta de dos partes que por razones históricas se denominan real e imaginaria. Hay varias formas de representarlos y una de ellas es como si se tratara de coordenadas. Por ejemplo:

z=(3, -2)

es un número complejo en el que la parte real (que siempre se escribe primero) vale 3, y la parte imaginaria vale -2. De manera más general diríamos que los números complejos se representan de la manera siguiente:

z= (a, b),

donde a y b son la parte real e imaginaria, respectivamente, y pueden ser números enteros o con decimales, positivos o negativos.

Para localizarlos en el plano se construye un sistema coordenado en el que el eje "x" se utiliza para señalar el valor de la parte real (eje real), y el eje "y" para la parte imaginaria (eje imaginario). Cuando se hace esto es posible construir una representación gráfica muy sencilla como la de la figura 7, donde como ilustración se localizan los números complejos: z= (4, 0), z=(0, 2) y z=(-3, -3).

Figura 7. Representación gráfica del plano complejo. La distancia R a la que está cada número complejo del origen es una medida de su tamaño.

Definir un nuevo conjunto de números es entretenido, pero poco útil si no lo acompañamos de reglas que permitan trabajar con ellos, por lo menos sumarlos y multiplicarlos. Para los números complejos esto ya está establecido y resulta relativamente fácil.

Si queremos hacer la suma de dos números complejos, z1= (a, b) y z₂= (c, d), basta sumar por separado sus partes reales e imaginarias:

z₁ + z₂ = (a, b) + (c, d) = (a+c, b+d).

Por ejemplo, si z₁ = (2, 1) y z₂ = (4, 3), su suma nos da:

z₁ + z₂=(2,1) + (4,3) =(2+4,1+3) = (6,4),

en donde el resultado z = (6, 4) también es un número complejo.

Para la multiplicación la regla es un poco más complicada, pero basta seguir la receta:

z₁ + z₂= (a, b) (c, d) = (ac - bd, ad + cb),

donde para obtener la parte real se toma el producto de los términos reales menos el producto de los imaginarios, y para la parte imaginaria se suma el producto de los términos cruzados (real por imaginario).

Así, si z₁ = (2, 1), y z₂ = (4, 3), al multiplicarlos se obtiene el número complejo:

z₁ + z₂ = (2, 1) (4, 3) = ((2 x 4) - (1 x 3), (2 x 3) + (1 x (5, 10).

Ahora tenemos ya todo listo: un conjunto de números y reglas para sumarlos y multiplicarlos, ¿por qué no usarlos entonces para jugar con sus iteraciones? Hacerlo constituye una de las posibles vías para generar fractales, y quizá sea la ruta que lleve a resultados más sorprendentes. Veamos cómo lograrlo.

PRIMERA SORPRESA, LOS CONJUNTOS DE JULIA

El trabajo pionero en el juego de hacer iteraciones con números complejos fue desarrollado por dos matemáticos franceses, Gaston Julia y Pierre Fatou, a principios de nuestro siglo. Sus resultados fueron la base sobre la que se construyó la revolución fractal de los ochenta. En particular, Benoit Mandelbrot recuperó su análisis sobre el comportamiento de los números complejos cuando la iteración consiste en elevarlos al cuadrado y sumar una constante al resultado. Simbólicamente diríamos:

Z_n + 1 = Z²n + c,

donde c es la constante y también es un número complejo. Esta iteración dice simplemente: toma un número y elévalo al cuadrado (multiplícalo por sí mismo), súmale la constante c que elegiste, y repite lo mismo una y otra vez sobre tus resultados. Las órbitas que ahora se generan son secuencias de números complejos y sus características dependen fundamentalmente de los valores del punto inicial z_o del que se parte y la constante c seleccionada.

Por ejemplo, si el punto inicial es z_o = (1, 0) y la constante c = (0, 1), al hacer la iteración tenemos:

Z₁ = z₀² + c = (1,0) (1,0) + (0,1) = (1,1)

Z₂ = z₁² + c = (1,1) (1,1) + (0,1) = (0,3)

Z₃ = z₂² + c = (0,3) (0,3) + (0,1) = (-9,1)

Z₄ = z₃² + c = (-9,1) (-9,1) + (0,1) = (80,-17)

y así podemos seguir hasta detectar la naturaleza del atractor. En este caso, cuando se representa la órbita sobre el plano complejo se ve que la iteración nos aleja cada vez más del origen (0,0) sin acercarse a ningún número complejo determinado. Decimos entonces que el atractor es el infinito y lo representamos diciendo que z =>ñ.

Desde 1906, Fatou había demostrado que para cada valor de c, la aplicación de esta iteración sobre todos los puntos del plano complejo genera órbitas que en su mayoría terminan en z =>ñ, salvo para un conjunto bien definido de puntos. En estos casos, la iteración detecta puntos fijos; órbitas periódicas donde se repite la misma secuencia de números después de cierto número de iteraciones, o puntos que escapan hacia atractores finitos. A este tipo de puntos cuya iteración NO escapa a infinito, podríamos llamarlos prisioneros, mientras los otros son escapistas.

Todos los puntos prisioneros pertenecen a lo que llamaremos el cuerpo de un conjunto de Julia. El conjunto, en sí, sólo está constituido por la curva que separa a los prisioneros de los escapistas; los puntos del conjunto de Julia también son prisioneros.

Para localizar los puntos que conforman el conjunto de Julia para una c dada, hay que recorrer el plano complejo buscando la frontera donde se pasa de tener órbitas que se disparan a infinito, a la región donde esto ya no sucede. El recorrido se convierte en un viaje inolvidable por el país de las maravillas.

En la actualidad, el viaje puede hacerse fácilmente si se tiene una computadora personal (Dewdney, 1987), y las figuras que se obtienen se ven extraordinarias cuando se reproducen en un monitor de color (ver las imágenes a color). Para los interesados, en el capítulo "Para la computadora" se explica la manera de hacer el recorrido, y en las figuras 8 y 9 se ilustra el tipo de resultados que se generan.

Figura 8. Conjuntos de Julia asociados a la iteración z_n+1 = z²_n+c. a) c = (0.12, 0.57); b) c= (-0.12, 0.66); c) c= (0.12, 0.74); d) c= (-0.25, 0.74); e) c= (-0.194, 0.6557); f) c= (0.75, 0.11).

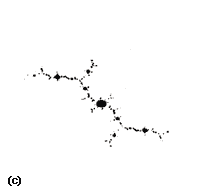
Figura 9. Conjuntos de Julia asociados a la iteración z_n+1 = z²_n+c. (a) c= (0.745, 0.113); (b) c= (1.25, 0); (c) c= (-0.1565, 1.0322); (d) c= (0.32 0.043); (e) detalle de la figura 8(c) en una amplificación del orden de 1/0.0001; (f) detalle de la figura 8 (c) en una amplificación del orden de 1/0.25.

Una observación cuidadosa del borde de estas figuras, donde los prisioneros están de negro y los escapistas de blanco, revela un hecho fundamental: la frontera o conjunto de Julia es un fractal y la curva total puede ser regenerada por cualquier trozo que de ella se elija. Esto es, el detalle del contorno se conserva a cualquier escala y de nuevo nos encontramos con una estructura autosimilar. Muestra de esto son las ampliaciones de los detalles arbitrariamente seleccionados de las figuras 8(c) y 8(e) que se presentan en las figuras 9(e) y 9(f), respectivamente. Como puede verse, la estructura de la frontera se repite a cualquier nivel de ampliación, y toda la información sobre la geometría del conjunto está codificada en el trazo de un solo punto sobre el papel: en la figura 9(f) hay un factor de aumento del orden de 4 y en la 9(e), de ñ10000! Viajar a lo largo del contorno de cualquiera de estas formas es perderse en el laberinto de un mundo infinitamente repetido, que de nuevo tiene longitud infinita y dimensión fraccional.

La increíble belleza de la representación gráfica de los conjuntos de Julia fue puesta en evidencia hace no más de 15 años por J. H. Hubbard, quien para hacerlo se sirvió de los grandes adelantos computacionales de nuestra época. El trabajo de Hubbard y Mandelbrot mostró la enorme riqueza de comportamientos que pueden generarse, y la marcada susceptibilidad de la estructura del conjunto ante ligeras variaciones del parámetro complejo c (Figuras 8(f) y9(a)).

Ante un mundo de posibilidades como éste, lo primero que se nos puede ocurrir es intentar hacer una clasificación. Pero, ¿cómo organizar formas que tienen tanto detalle?, en qué propiedad común podemos basarnos? Además, hay que considerar que cada valor de c da lugar a un conjunto de Julia distinto, ¿cómo clasificar entonces un número infinito de formas? La respuesta a estas preguntas fue dada en 1980 por Benoit Mandelbrot y las conclusiones que obtuvo son otra muestra clara de su enorme intuición visual.

EL FAMOSO CONJUNTO DE MANDELBROT

Del análisis de las figuras 8 y 9 se hace evidente que existen dos clases principales de conjuntos de Julia: aquellos para los cuales el cuerpo está formado por una sola pieza (el área del cuerpo se dice que es conexa, figuras 8(a)-(c) y 9(a)-(d), y otros en los que el cuerpo está desmembrado en infinitas colecciones de puntos más o menos aisladas (el área del cuerpo es disconexa, figuras 8(d)-(f). A estos últimos también se les llama conjuntos de Cantor o polvos de Fatou.

Esta distinción geométrica da pie a la posibilidad de separar los valores del parámetro complejo c en dos conjuntos bien diferenciados: los que en la iteración Z_n+1 = Z²_n+ c dan lugar a figuras conexas, y disconexas.

En principio, el trabajo de construirlos puede parecer una locura, pues se necesitaría analizar las posibilidades de un número infinito de sistemas. Sin embargo, para hacerlo, Mandelbrot aprovechó un teorema probado de manera independiente por Julia y Fatou alrededor de 1919.

ATENCIÓN: Es posible demostrar que todos los valores de c que dan lugar a conjuntos de Julia conexos (áreas de una sola pieza) comparten la propiedad común de producir órbitas que NO se disparan a infinito cuando se aplica la iteración sobre el punto z₀ (0,0); esto es, el punto z_o = (0,0) es prisionero. Si z₀ = (0, 0) se comporta como escapista, la forma producida es necesariamente disconexa.

Las implicaciones del teorema son sorprendentes; basta aplicar la iteración en un solo punto, el z₀ = (0, 0), para determinar la naturaleza del conjunto de Julia que se obtendrá cuando la iteración se aplique a todo el plano complejo.

Benoit Mandelbrot fue el primero en aprovechar esta propiedad de la iteración cuadrática y se dedicó a localizar los valores de la constante c que dan lugar a conjuntos de Julia conexos. Al hacerlo se encontró con que esta colección de valores de c, que en su honor tiene el nombre de conjunto de Mandelbrot, también tenía una estructura sorprendente cuando se representaba en el plano complejo. De nuevo, en el capítulo "Para la computadora" se describe cómo generar por medio de la computadora la representación gráfica del conjunto de Mandelbrot y sus detalles, que se ilustran en las figuras 10 y 11.

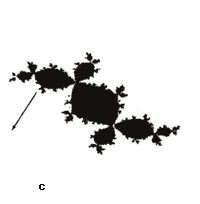
Figura 10. a) Conjunto de Mandelbrot. Se indican sobre la figura las regiones cuyo detalle se amplifica en las figuras 11 (a) y 11(b). (b) Contorno del conjunto de Mandelbrot. Se señala la localización de los valores del parámetro c que dan lugar a los conjuntos de Julia de las figuras 8 y 9. Los puntos 8(f) y 9(a) se encuentran en el denominado Valle de los hipocampos.

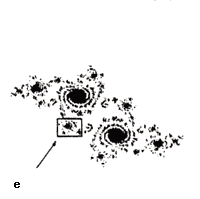
Figura 11. Detalles de la frontera del conjunto de Mandelbrot. Las figuras 11(d) y 11(f) son amplificaciones de regiones contenidas en el cuadro que les antecede.

Hay dos maneras de comenzar a describir la estructura geométrica del conjunto de Mandelbrot (Figura 10); una informal, que se refiere a él como la representación de un muñeco de nieve recostado y completamente infestado de granos; la otra, más purista, que considera que el cuerpo principal puede pensarse como una forma cardioide (de corazón) tangente a un disco circular de menor extensión, de los cuales brotan una infinidad de estructuras que se ajustan a la misma descripción. Es difícil decir que se trata de una figura cuya frontera es endiabladamente complicada, pues a toda escala aparecen formas geométricas semejantes a la original, conectadas a través de filamentos que siguen patrones muy poco regulares. Y así, aunque a simple vista el borde parezca estar salpicado de puntos aislados, puede demostrarse que el conjunto total es conexo (de una sola pieza), ya que siempre puede hallarse, a cierta escala, un filamento que cubra la ruta entre dos puntos aparentemente separados.

El conjunto de Mandelbrot parece ser un fractal en el sentido que hasta ahora hemos manejado. La ampliación de un detalle de su frontera (Figura 11(a)) da lugar a una forma muy similar a la del conjunto completo, y tal parece que esto se repetirá a cualquier escala. Sin embargo, las cosas no suceden exactamente de esta manera. los retoños de nuestro hombre de nieve resultan ser mas peludos y están más despeinados que su padre, y en plena lucha generacional las cosas se agravan con cada nuevo descendiente (Figura 11(b)). Como veremos más adelante, a entidades como ésta se les sigue clasificando como fractales, pero se les agrupa dentro de una clase particular denominada fractales no lineales; en ellos se pierde la autosimilitud en sentido estricto, pues cada cambio de escala introduce rasgos peculiares.

Quizá el propósito principal de construir el conjunto de Mandelbrot reside en desentrañar de qué manera se relacionan la posición de un valor del parámetro c dentro de él y la estructura del conjunto de Julia que se generará cuando se le utilice para aplicar la misma iteración a todo el plano complejo. Hoy se sabe que el conjunto de Mandelbrot es mucho más que una tabla de clasificación para distinguir entre formas conexas y disconexas. En realidad, contiene toda la información sobre las propiedades geométricas de cada conjunto de Julia, pero codificada como en un jéroglífico. En sí mismo es el recipiente de una colección completa de versiones reducidas y deformadas de cada uno de ellos.

Así, por ejemplo, todo valor de c que cae dentro del cuerpo del principal en el conjunto de Mandelbrot da lugar a una forma de Julia con apariencia de círculo arrugado (Figura 8(a)). Si el valor elegido se encuentra dentro de uno de sus primeros retoños, los círculos se multiplican (Figura 8(c)), y si se le desplaza hacia uno de los filamentos que surgen de él, las estructuras se adelgazan hasta generar una forma dendrítica (Figura 9(c)).

Un reto a nuestra capacidad de asombro consiste en hacer una visita a la región del conjunto de Mandelbrot conocida como el valle de los hipocampos (Figura 10(b)). Los valores de c comprendidos en esta región dan lugar a conjuntos de Julia como los de la figura 9(a). Estructuras como ésta inundan el valle con formas geométricas que simulan caballos marinos enlazados de múltiples maneras (Figuras 11(c) ñ 11(f)); un verdadero paraíso de Neptuno a escalas diversas.

El contorno del conjunto de Mandelbrot es sin duda alguna su secreto más apasionante. Es ahí donde se define todo el futuro del reino habitado por los conjuntos de Julia. Si tomáramos una ruta que nos llevara desde el interior del conjunto de Mandelbrot y, cruzando a través de la frontera, nos depositara en su parte externa, seríamos testigos del equivalente a una verdadera "transición de fases" geométrica. Un análisis de los conjuntos de Julia visitados nos mostraría cómo éstos comienzan a desgajarse., desmoronarse, y finalmente son víctimas de una explosión violenta que los desmenuza en mil pedazos al atravesar la frontera. Como ejemplo tenemos las figuras de la 8(a) a la 8(d) que corresponden a la ruta trazada sobre el conjunto de Mandelbrot de la figura 10(b), y que nos lleva del interior al exterior del conjunto.

Los detalles de la estructura del contorno del conjunto de Mandelbrot se hacen más evidentes cuando se utilizan colores para distinguir las características de la órbita de iteración que le corresponde a cada valor de la constante c. Al hacerlo se producen imágenes de enorme belleza (véanse las láminas) dignas de ser consideradas como verdaderas obras de arte, las cosas han llegado tan lejos que hay quien considera que tienen poderes relajantes sobre aquel que las observa con detenimiento.

La creación de un universo extraordinario poblado de hipocampos, dragones, hombres de nieve, flores y caracoles de extrema complejidad de diseño, no es una particularidad única de la iteración cuadrática que hemos estudiado. Existen numerosos casos de relaciones matemáticas que son capaces de construir su propio mundo fractal (Peitgen, 1986). El análisis y clasificación del zoológico de sus formas ha mostrado a los seres humanos una nueva forma de generar, almacenar y transcribir información. El juego con iteraciones de números complejos es un mecanismo sencillo para generar estructuras altamente organizadas, utilizando una sola clave. Ilustra con mucha claridad cómo la presencia de una estructura compleja no necesariamente implica un mecanismo de formación igualmente complicado. Esto hace pensar que, para nuestra sorpresa, la gran similitud con el comportamiento de la naturaleza, en el que la lectura de un solo código puebla nuestro mundo de formas diversas, puede ser más que mera coincidencia.