IV. UN MUNDO DE IMÁGENES

LOS fractales son, sin duda alguna, mucho más que interesantes curiosidades matemáticas con las cuales alimentar nuestra fantasía. En ellos reside la esencia del vastísimo lenguaje de una nueva geometría que permite describir objetos y formaciones a través de expresiones extraordinariamente compactas.

Sin embargo, a diferencia de la geometría euclidiana, en donde los elementos básicos pueden generarse de manera directa (líneas, círculos, planos, etcétera), en la geometría fractal las formas primarias son conjuntos de procedimientos matemáticos (algoritmos) que se encargan de rotar, trasladar, reescalar o deformar figuras de una manera particular.

En este sentido, podemos decir que la geometría fractal está constituida por una infinidad de elementos, cada uno de los cuales representa una transformación geométrica completa y única. Como los símbolos gráficos del chino y el japonés, cada algoritmo fractal funciona como un ideograma que transmite un mensaje global característico.

Los códigos matemáticos que subyacen en toda estructura fractal son parte de un concepto que los matemáticos denominan transformaciones generales de afinidad en el plano. Éstas no son más que reglas para escalar, rotar, desplazar y, en ocasiones distorsionar un objeto geométricamente. Lo que se puede hacer con ellas es impresionante: la hoja de un helecho, la planta completa, el bosque donde colocarla, las montañas que lo rodean, o mejor, todo el planeta. La creación y recreación de paisajes, la codificación, reproducción y transmisión de imágenes, todo está al alcance de la mano del que esté dispuesto a intentarlo.

TRANSFORMANDO

La naturaleza de cualquier transformación de afinidad permite clasificar a ésta dentro de dos grandes grupos: lineales y no lineales. La diferencia fundamental entre ellas reside en que las primeras respetan las líneas rectas que constituyen la forma geométrica sobre la que se aplican, mientras que las segundas no, y por tanto actúan sobre ellas alterando algo más que su posición, orientación y tamaño.

En ambos lenguajes, lineal o no lineal, el número de algoritmos básicos que puede construirse es infinito, pero mientras las reglas del primer dialecto son mucho más sencillas, la riqueza de posibilidades del segundo lo hacen especialmente atractivo.

Para ayudar a que todo esto cobre sentido, veamos, poco a poco, cómo generar la estructura global de una transformación de afinida lineal (Peitgen, 1992).

Tomemos como figura geométrica inicial un cuadrado de lado L y situémoslo en un sistema de referencia arbitrario, de forma tal que su vértice inferior izquierdo coincida con el origen (Figura 12(a)). Cada punto en la frontera o dentro del cuadrado puede así caracterizarse por un par de coordenadas (x, y), donde "x" y "y" representan números que siempre son mayores que 0 pero menores que L.

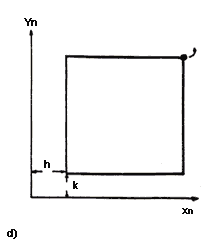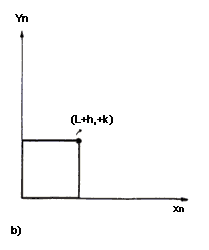
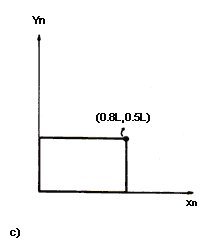
Figura 12. Se ilustra el resultado de aplicar diversas transformaciones sobre la figura de base representada en (a). (b) Transformación de similitud con un factor de escala r = 0.5. c) Transformación de afinidad con r= 0.8 y s= 0.5. d) Desplazamiento x_n = x + h, y_n = y + k.

¿Cómo construir una transformación geométrica que aplicada sobre cada punto de este cuadrado dé lugar a una forma similar; pero de la mitad de tamaño que la original?

El problema se resuelve fácilmente si consideramos que las coordenadas de todo punto en la nueva figura, que llamaremos (x_n, y_n) para distinguirlas, pueden generarse a partir de las de la primera (x, y) siguiendo una regla que reduzca todo a la mitad, tanto en la dirección x como en la y:

X_n = 0.5*x

X_y = 0.5*y.

Para ilustrarlo basta, por ejemplo, aplicar la receta anterior a las coordenadas de los cuatro vértices del cuadrado inicial:

(0,0)---> (0.5*0, 0.5*0)---> (0, 0)

(0, L)---> (0.5*0, 0.5*L)---> (0, L/2)

(L, 0)---> (0.5*L, 0.5*0)---> (L/2, 0)

(L, L)---> (0.5*L, 0.5*L)---> (L/2, L/2)

con lo que se obtiene el pequeño cuadrado de la figura 12(b). En un caso como éste se dice que la transformación ha introducido un factor de escala r=0.5.

Debe ser claro, entonces, que para aumentar o disminuir el tamaño de una figura por un factor de escala r arbitrario, se requiere simplemente aplicar la transformación

X_n = r*x

Y_n = r*y

a cada uno de los puntos que la constituyen. La forma así generada es similar a la original, pero más grande que ella si r es mayor que 1 o más chica si r es menor que 1. Como la figura no ha sido deformada se dice que se ha hecho una transformación de similitud.

Si para ampliar el número de posibilidades se utilizan parámetros de escala distintos para cada coordenada, "x" y "y", de manera que:

X_n = r*x.

Y_n = s*y,

el resultado de la transformación geométrica ya no es un cuadrado regular. Por ejemplo, si r=0.8 y s=0.5, lo que obtendremos es un rectángulo más largo que ancho, como el de la figura 12(c); sin embargo, se vale decir que sigue siendo una forma geométrica "afín" a la inicial (Figura 12(a)). Esta transformación de carácter más general se conoce como transformación de afinidad.

La estructura de reglas geométricas como éstas se enriquece si además de reescalar la figura permiten trasladarla a otro sitio o rotarla. Analicemos cómo lograrlo.

Para desplazar nuestro cuadrado de lado L a cualquier región del espacio es importante notar que todo cambio en la posición de una figura puede descomponerse en desplazamientos simples paralelos a cada uno de los ejes del sistema de referencia elegido: primero la movemos horizontalmente y luego verticalmente, o al revés. Sin embargo, para asegurar que la forma mantiene su estructura durante el proceso, es necesario que todos los puntos en ella se trasladen de la misma manera. Por ejemplo, si queremos mover la figura 12(a) una unidad en la dirección x y otra unidad en la dirección y, deberemos sumar un uno a todas las coordenadas del cuadrado:

X_n = x+1

Y_n = y+l.

Si generalizamos esto para cualquier traslación que mueva la figura h unidades en x, y k unidades en y, tendremos:

X_n = x+h

Y_n = y+k,

como se representa en la figura 12(d).

Ahora, siendo más ambiciosos, ¿qué hacer para trasladar y reescalar simultáneamente la forma geométrica? Pues como cada cosa se puede hacer de manera independiente, basta ponerlo todo junto:

X_n = r*x + h

Y_n = s*y + k

y aplicar la misma transformación a todos los puntos de la figura que nos interese. Que quede claro, lo que multiplica, reescala; lo que se suma, traslada.

Para completar estas ideas debemos ahora considerar los efectos de una rotación, con lo que tendremos la posibilidad de hacer prácticamente lo que queramos. En este punto solicitaremos del lector un acto de fe, que más que ahorrarnos lágrimas nos evitará presentar una explicación demasiado larga.

Cuando se desea rotar una figura cuyos puntos se designan con las coordenadas (x, y), basta aplicar sobre todos ellos la siguiente transformación para obtener las coordenadas (X_n, Y_n) de la nueva figura:

X_n = x*cos (A) - y*sen(B)

Y_n = x*sen(A) + y*cos(B).

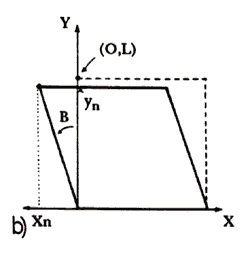
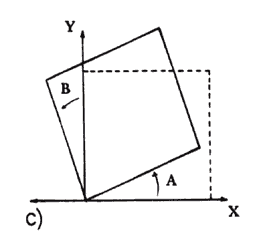
Aquí hay que calcular el coseno y el seno de A y B, que son los ángulos en que se rotan los lados horizontales y verticales de la figura original, medidos con respecto a los ejes "x" y "y", respectivamente. Por ejemplo, si rotamos el cuadrado de la figura 12(a) un ángulo A, pero B = 0, sólo rotarán los lados horizontales (Figura 13(a)); si por el contrario, A = 0 pero B tiene cierto valor, rotarán los lados verticales (Figura 13(b)). La figura 13(c) muestra el resultado de combinar ambos efectos. Es importante señalar que A y B son positivos si se miden, a partir de su eje de referencia, en sentido contrario a las manecillas del reloj; en el otro caso se consideran negativos.

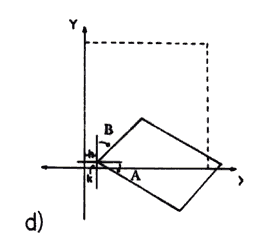Figura 13. (a) Efecto de la rotación de un ángulo A de los lados horizontales de la figura de base que se representa con líneas discontinuas. (b) Efecto de la rotación de un ángulo B de los lados verticales. c) Rotación general obtenida por la combinación de las dos anteriores. d) Efecto de la aplicación de la transformación de afinidad lineal descrita en el texto.

Con estos antecedentes podemos ya presentar la estructura global de una transformación de afinidad lineal que sea capaz de modificar el tamaño, posición y orientación espacial de una forma geométrica cualquiera. En este camino,

si r y s son parámetros de escala para las coordenadas "x" y "y" respectivamente, h y k son una medida de los desplazamientos honzontal y vertical y A y B son los ángulos que determinan la naturaleza de la rotación, tenemos:

X_n = r* x* cos (A) - s* y* sen(B) + h

Y_n = r* x* sen (A) + s* y* cos(B) + k,

la cara completa de la transformación que buscábamos (Peterson, 1988).

Para ilustrar los efectos generales que resultan de realizar una transformación de afinidad lineal como ésta sobre una figura cualquiera, consideremos el caso descrito en la siguiente tabla:

r	s	h	k	A	B
3/4	1/2	1/2	1/4	-30ñ	-45ñ

y apliquémosla a nuestro ya famoso cuadrado de longitud L.

En estas circunstancias, los vértices originales de la figura se desplazan a las posiciones

(0,0)--->(1/2, 1/4)

(L,0)---> (0.65*L + 1/2, -0.375*L + 1/4)

(0,L)---> (0.35*L + 1/2, 0.35*L + 1/4)

(L,L)---> (1.0*L + 1/2, -0.02*L + 1/4)

y la forma resultante, reducida, rotada y trasladada (pero aún con fronteras rectas), toma la estructura que se indica en la figura 13(d). Así vemos que una definición de tablas de transformación como la anterior nos permite producir prácticamente la deformación que sea, siempre y cuando nos conformemos con mantener las líneas rectas, "rectas". Lo más importante es que el nuevo dialecto de los fractales lineales se basa completamente en ellas.

Todo fractal lineal puede construirse aplicando reiteradamente un conjunto determinado de transformaciones de afinidad lineales sobre cierta región del espacio. En ese sentido, todo el detalle de una forma fractal puede quedar almacenado en un conjunto de tablas de transformación como la descrita. Esta manera de concebir las cosas es útil en la medida que tengamos acceso a un método que permita extraer la imagen codificada en ellas. Como la técnica existe, nuestro problema está solucionado.

PING-PONG FRACTAL

En la década pasada, M. Barnsley y sus colaboradores desarrollaron una estrategia de trabajo que permite reproducir prácticamente cualquier fractal. La idea básica es desde el principio artística y entretenida: hágase primero un collage para después jugar sobre él un ping- pong fractal.

En el método de Barnsley el trabajo se inicia buscando un conjunto de transformaciones de afinidad, que al aplicarse sobre una figura de base arbitraria (como nuestro cuadrado de lado L), dé lugar a nuevas formas que, acomodadas o superpuestas como en un collage, reproduzcan algo que se parezca a la imagen del fractal que se quiere construir.

Por ejemplo, en la reproducción del triángulo de Sierpinski de la figura 14(c) bastaría tomar como base inicial un triángulo y generar tres transformaciones de afinidad que además de reducirlo a la mitad, trasladen los resultados hacia cada uno de sus vértices (Figura 14(a)). Las transformaciones correspondientes pueden condensarse en una tabla como la siguiente:

	r	s	h	k	A	B
1	0.5	0.5	0	0	0	0
2	0.5	0.5	0.5	0	0	0
3	0.5	0.5	0.25	0.5	0	0

Cuando los resultados de las tres transformaciones se dibujan juntos (se hace el collage), se ve que representan el esqueleto del triángulo de Sierpinski (Figura 14(b)).

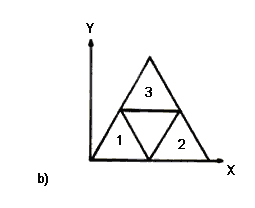
Figura 14 (a) Representación de las tres transformaciones de afinidad necesarias para generar el triángulo de Sierpinski. b) Collage obtenido de la superposición de las formas generadas al aplicar las transformaciones anteriores. c) Resultado de jugar ping-pong fractal sobre el collage de la figura (b).

Una vez que se ha identificado el número mínimo de transformaciones que permiten generar el esqueleto del fractal, puede iniciarse el juego con un ping-pong muy especial.

Si analizamos la estructura geométrica del triángulo de Sierpinski podemos darnos cuenta de que un mecanismo simple para reconstruirlo podría basarse en la aplicación sucesiva de las anteriores transformaciones de afinidad sobre cada una de las tres regiones triangulares generadas. De esta forma, repitiendo el proceso a toda escala produciríamos la imagen del fractal (Figura 14(c)). Sin embargo, poner en práctica este procedimiento puede ser muy engorroso, pues es necesario transformar una gran cantidad de puntos en un orden bien determinado.

Barnsley y su grupo lograron demostrar que el mismo objetivo podría alcanzarse siguiendo un camino distinto, el cual, al menos desde el punto de vista de la operación por computadora, resulta menos costoso.

Imaginemos una mesa de ping-pong para tres jugadores formada por canchas triangulares, dispuestas tal y como se indica en la figura 14(b). Para iniciar el juego, el juez del partido lanza una pelota entintada sobre alguna de las canchas y grita un número arbitrariamente elegido entre 1 y 3 (correspondiente a alguna transformación de afinidad). En estas circunstancias, el jugador que recibe la pelota deberá dejarla botar en su cancha, localizar su posición dentro de ella (la pelota dejará una marca en el punto (x, y)), y lanzarla al punto que corresponda, (X_n, Y_n), después de aplicar la transformación de afinidad voceada por el juez. Si el jugador acierta el tiro (y siempre lo hace), el árbitro deberá elegir otro número al azar (entre 1 y 3) para que quien tenga la pelota en su cancha, registre de nuevo la posición del bote y conteste buscando atinar a la coordenada resultante de aplicar la transformación que ahora le corresponde. Continuando de esta forma con el juego y confiando en la habilidad de los deportistas, podemos preguntarnos después de un tiempo razonable, qué figura se ha formado sobre la cancha después de tanto rebote. La respuesta quizá parezca sorprendente, pero el campo de juego completo reproducirá la imagen de nuestro fractal triangular (Figura 14(c)).

La propuesta de principio es entonces genial. Basta, para construir el fractal, elegir de modo arbitrario un punto inicial y a partir de él aplicar reiteradamente las transformaciones de afinidad en un orden seleccionado al azar. Si se dibuja sobre un plano la órbita de la iteración así generada, la figura obtenida reproducirá la estructura del fractal cuyo esqueleto esté descrito por el conjunto de transformaciones de afinidad con el que se preparó el collage original.

Bajo este principio podríamos preguntarnos, ¿cómo reproducir la carpeta de Sierpinski de la figura 5(b)? En este caso, la forma de partida puede ser un cuadrado o rectángulo al que hay que aplicar ocho transformaciones de afinidad. Cada una de ellas se encargará de producir un nuevo cuadrado o rectángulo tres veces más pequeño que el original, trasladado a manera de generar un collage como el siguiente:

Ahora tan sólo nos queda jugar con él al ping-pong fractal.

En estos dos ejemplos todas las transformaciones de afinidad utilizadas generan formas básicas de área similar. Cuando esto no sucede es necesario modificar un poco las reglas del juego, con el fin de asegurar que cada cancha será visitada un número de veces proporcional a su extensión en el espacio.

Para ilustrarlo apliquemos las siguientes cuatro transformaciones de afinidad sobre una figura inicial de forma rectangular:

	r	s	h	k	A	B
1	0.0	0.16	0.0	0.0	0.0	0.0
2	0.3	0.37	0.0	0.44	135	-40
3	0.3	0.34	0.0	1.6	45	45
4	0.85	0.85	0.0	1.6	-1.5	-1.5

La superposición de los resultados da lugar a un esqueleto como el de la figura 15 (a), donde el polígono resultante de aplicar la última transformación de afinidad es el de mayor área.

Al jugar ping-pong fractal sobre este collage, asegurando que la probabilidad de visita de cada región espacial (p₁) sea proporcional a su área:

P₁=0.005           p₂=0.0975            p₃=0.0975           p₄=0.8

el resultado es una increíble hoja de helecho con estructura fractal (Figura 15(b)), en la que cualquiera de sus partes es similar al total. ñUna imagen tan compleja contenida en sólo cuatro formaciones de afinidad! Una imagen que, para los interesados, puede reconstruirse con increíble facilidad (véase el capítulo "Para la computadora").

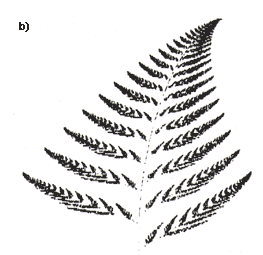
Figura 15. (a) Collage que sirve de base para la construcción de la hoja de helecho fractal del inciso b).

Utilizar en forma práctica el método de Barnsley para la construcción de fractales requiere en gran medida de una interacción estrecha entre el observador y la computadora. Sólo así puede encontrarse el conjunto mínimo de transformaciones de afinidad que permitirá reproducir la imagen deseada. Procediendo de esta manera existe la posibilidad de desarrollar nuestro espíritu creativo y diseñar desde pequeños arbustos (Figura 16) hasta los más complejos paisajes fractales. ¿Por qué no probar y construir su catálogo personal de imágenes fractales? Todo se vale.

Figura 16. a) Superposición de las formas obtenidas al aplicar las siguientes transformaciones de afinidad sobre una figura rectangular:

	r	s	h	k	A	B
1	0.47	0.12	0.77	0.77	80	-50
2	0.49	0.66	0.42	0.75	60.5	47.8
3	0.53	0.55	0.9	1.3	-20.6	-48.9
4	0.53	0.76	0.6	0.1	-10	-2

b) Fractal generado al jugar ping-pong sobre el collage anterior (p₁ =0.05, p₂= 0.3, p₃ = 0.3, p₄=0.35).

Y TODAVÍA HAY MÁS

La riqueza de los diseños finales que se obtienen puede incrementarse notablemente si se incopora el uso de tranformaciones de afinidad no lineales. Como ya lo mencionamos, en este caso la aplicación de un algoritmo deforma las líneas rectas de la figura original, dando lugar a nuevas estructuras cuya apariencia tiene poco que ver cxon la de aquella.

Para poner un ejemplo, baste decir que son suficientes dos transformaciones de afinidad no lineales (Jñrgens, 1990) para recuperar las intrincadas formas de los conjuntos de Julia presentados en el capítulo anterior. Jugando ping-pong fractal con ellas se obtienen resultados como los que se muestran en la figura 17.

Figura 17. Formas de Julia obtenidas jugando ping-pong fractal con dos transformaciones de afinidad no lineales. a) c=(-0.12, 0.74); b) c=(0.1565, 0.322); c) c=(1.25, 0); d) c=(0.32, 0.043).

¿Qué más se puede pedir? Con un poco de paciencia y cierta dosis de creatividad podemos generar prácticamente lo que queramos, con un nivel de detalle que en muchas ocasiones resulta inimaginable.

Todo esto, por supuesto, sólo es una muestra de la enorme potencialidad práctica de la geometría de los fractales. En la actualidad su uso ha permitido reducir significativamente la cantidad de datos necesarios para transmitir almacenar o simular casi cualquier imagen. Hoy día, de manera sistemática, la escena de interés (fotografía o video) es trasladada a la computadora, donde se analiza y secciona en trozos de diversos tamaños, asegurando que el color o tono dentro de ellos se mantenga relativamente constante. Elegidas así las piezas del collage, se inicia la búsqueda sobre una enorme variedad de transformaciones de afinidad (existen catálogos para formas estándar) del conjunto de algoritmos necesarios para reproducirlas. La imagen queda entonces codificada como un sistema de funciones que se almacena o transmite con facilidad. Posteriormente, si se quiere recrear la escena original, sólo es necesario seguir las reglas del ping-pong fractal; y aún más, la reconstrucción puede hacerse de manera secuencial con el fin de generar imágenes animadas en las que es posible incluir hasta treinta figuras distintas en cada segundo.

La técnica de Barnsley (o más formalmente, el método de sistemas de funciones iteradas) no es el único camino que se conoce para obtener fractales que simulan la estructura de objetos naturales. En particular, las características de fractales clasificados como aleatorios han sido fuertemente explotadas en este terreno.

Un fractal se considera aleatorio cuando en su construcción intervienen elementos condicionados por el azar. Por ejemplo, imaginemos que queremos reproducir el perfil de una montaña partiendo de una figura regular como un triángulo (Figura 18(a)). Iniciemos el trabajo localizando los puntos medios de cada lado, y desplacémoslos verticalmente a una distancia d_i determinada por algo que produzca números aleatorios. Si unimos con líneas los puntos desplazados (Figura 18(b)), la forma resultante estará constituida por cuatro triángulos más pequeños, que a diferencia de los obtenidos por el método de Barnsley para la carpeta de Sierpinski, no son necesariamente iguales. Si sobre cada una de estas nuevas partes se repite el mismo procedimiento (Figura 18(c)), y se continúa haciéndolo sobre las figuras resultantes (Figura 18(d)) hasta que sea imposible distinguir los lados de cada triángulo, el resultado será una estructura poligonal muy rugosa y compleja que con un manejo adecuado de tintes, luces y sombras puede convertirse en una excelente reproducción de una montaña.

Figura 18. Construcción gráfica de una fractal aleatorio. La estructura final simula una montaña.

Aplicando el mismo procedimiento sobre figuras poligonales diferentes a nuestro triángulo, pueden generarse paisajes montañosos que exhiben tanto detalle como el de una verdadera fotografía.

En la recreación de un paisaje fractal la mayoría del tiempo y esfuerzo que se emplea no se gasta en el trabajo matemático de construir las diferentes estructuras geométricas que formarán la composición, sino en los detalles artísticos de selección de colores, texturas y sombras. Los investigadores y los artistas trabajan juntos estudiando las características del reflejo de la luz sobre diversas superficies, o los mecanismos para hacer resaltar una estructura particular. El resultado es una obra de arte en todos los sentidos.

Otros métodos de simulación de imágenes desarrollados por B. Mandelbrot y sus colaboradores recurren al uso de los patrones generados en caminatas aleatorias o señales de ruido de radiofrecuencia, para generar los contornos de costas, nubes o macizos rocosos. En este caso, aunque las escenas obtenidas pueden ser muy realistas, existen serias desventajas asociadas al hecho de que la técnica no es sistemática y requiere de un largo periodo de prueba y error.

Las diversas rutas que pueden seguirse para crear entidades fractales semejantes a objetos reales, junto con el método descrito para "comprimir" escenas y automatizar la reproducción de paisajes, abren las puertas a un mundo de increíbles posibilidades. La transmisión de fotografías e incluso de películas por vía telefónica, así como la recreación de universos imaginarios que sirvan de escenografía al cine de ciencia ficción de los próximos años son sólo dos ejemplos de los muchos proyectos que están en desarrollo.

Los fractales que se obtienen por métodos matemáticos o geométricos como los hasta ahora descritos son en ocasiones demasiado regulares y perfectos como para servir de modelo para patrones naturales. Esto ha llevado a tratar de incluir en los algoritmos matemáticos las características conocidas sobre los procesos de crecimiento y formación de objetos reales. De esta manera, y poco a poco, los fractales aparecen como herramientas fundamentales en el trabajo de no pocos físicos, químicos y biólogos.

El conocimiento de las reglas básicas de la geometría de los fractales está revolucionando nuestras concepciones sobre las formas y su imagen, su gestación y crecimiento, dotándonos de nuevas armas para descifrar algunas de las claves que rigen los astutos juegos de la naturaleza.