V. JUEGOS NATURALES

HEMOS insistido hasta el cansancio que los fractales están por todas partes y que las características de su estructura los hacen particularmente adecuados para describir la geometría de una infinidad de formas naturales. Ahora surgen las preguntas inevitables: ¿Por qué? ¿Qué tipo de mecanismo o proceso de crecimiento los produce? ¿Qué se esconde detrás de la formación de un fractal en el mundo real?

Para contestar estas preguntas lo primero que hay que hacer es tratar de ser lo más honestos posible. Por principio de cuentas, si bien es cierto que los fractales son en muchos casos buenas aproximaciones de la realidad, la verdad es que no hay estructura real que soporte ser ampliada repetidamente un número infinito de veces y siga mostrando la misma cara; para todo hay límites. A nivel microscópico llegará el momento en que la figura se desdibuje y nos encontremos con los átomos y las moléculas; a nivel macroscópico siempre hay una frontera en la que el objeto real cambia de un tipo de patrón a otro.

Por otra parte, como las estructuras fractales han aparecido en áreas tan distintas como la distribución de galaxias en el Universo y la propagación de enfermedades infecciosas, es todavía muy pronto para decir si se trata de problemas diferentes que requieren de una explicación particular, o si hay un principio general único que permite explicarlo todo.

Han surgido así diversos modelos que consideran las características físicas, químicas o biológicas del sistema de interés y proponen mecanismos de crecimiento que dan lugar a estructuras fractales muy semejantes al objeto real. Las distintas propuestas contienen ingredientes comunes que hacen pensar en la presencia de principios universales, pero no todo es claro y pocos se atreven a aventurarse.

Hay maneras muy sencillas de generar estructuras fractales en un laboratorio, o aun en la casa, si se tiene el equipo adecuado. El análisis de su crecimiento permite obtener pistas sobre los mecanismos que se han encargado de inundar la naturaleza con formas fractales. Algunos de los ejemplos más ilustrativos los encontramos al realizar experimentos en electroquímica o sobre flujo de fluidos; detengámonos un poco en ellos para comprenderlos.

AGREGADOS FRACTALES

Cuando uno se pregunta cómo se forma una roca, un diamante o un cristal de cuarzo, las respuestas que se obtienen son muy distintas. Un cristal perfecto, por ejemplo, se forma normalmente en condiciones de equilibrio donde las partículas que lo constituyen se agregan muy lentamente y pueden cambiar de posición un sinnúmero de veces. Sin embargo, en la mayoría de los casos no hay tiempo para tantos lujos; la formación de objetos naturales, desde montañas hasta seres vivos, se da en condiciones muy alejadas de la situación de equilibrio y a través de procesos irreversibles (Sander, 1987).

Tal es el caso de una categoría especial de objetos fractales que durante los últimos años ha merecido la atención de muchos científicos: los denominados agregados fractales (Matsushita, 1984). Se trata de sistemas en los que una gran cantidad de partículas se agrupan para generar un cuerpo con estructura irregular y son muy familiares a los químicos, pues se les obtiene en procesos de sedimentación, electrodeposición, floculación y agregación de coloides, aerosoles, polvos, etcétera. En particular, la formación de agregados fractales metálicos que se depositan electroquímicamente sobre superficies que tienen geometrías diversas, ha impulsado un nuevo campo de investigación que rinde frutos importantes en el área de tecnología de pilas y baterías.

Para entender mejor qué es y cómo se forma un agregado fractal por electrodeposición electroquímica hasta hacer el siguiente experimento (Talanquer, 1991):

El material necesario consiste en dos pedazos de vidrio de ventana en forma de disco circular de 15 cm de diámetro, dos trozos de alambre de cobre de 1 mm de diámetro transversal, una pila de 1.5 ó 5V, masking-tape, una jeringa y disoluciones de sulfato de cinc (ZnS04) a diversas concentraciones (por ejemplo, 1 g de ZnS04 en 100 ml de agua u 8 de la sal en 100 ml de agua).

Con el alambre de cobre se construyen los electrodos: uno de ellos, con forma de círculo de 10 cm de diámetro, se coloca entre las placas de vidrio, centrándolo con respecto a una pequeña perforación hecha en la placa superior; para el otro se corta un trozo recto de alambre que se introduce en el agujero central (Figura 19).

Para mantener los discos de vidrio juntos basta colocar en el borde unas tiras de masking-tape, y la disolución de sulfato de cinc se inyecta con una jeringa a través de la perforación, asegurando que cubra uniformemente la región entre el orificio y el electrodo circular.

El experimento comienza cuando el polo negativo de la pila se conecta al electrodo central (cátodo) y el positivo al electrodo circular (ánodo).

Figura 19. Esquema de la celda electroquímica para el crecimiento de un agregado fractal.

La diferencia de potencial aplicada entre los electrodos hace que los iones cinc migren hacia el electrodo central y se depositen sobre él. Al cabo de unos cuantos minutos se ve la formación de un agregado metálico que comienza a ramificarse en todas direcciones y que alcanza un diámetro considerable ( 6 cm) después de una hora de crecimiento.

La estructura final del agregado depende tanto de la concentración de la sal como del voltaje aplicado (Argould, 1988; Kahanda, 1989). Se han identificado así al menos cuatro tipos de patrones distintos (Grier; 1986; Sawada, 1986): fractales y homogéneos (Figuras 20 (a) y (b)), dendríticos y filiformes (Figuras 20(c) y (d)). Los primeros dos son agregados desordenados que crecen lentamente y, como veremos, tienen dimensión fraccional; los segundos tienen estructura cristalina y se forman con más rapidez. De hecho, es posible construir una especie de diagrama de fases donde se localiza la concentración y el voltaje, en la que aparece cada una de estas estructuras (Figura 21). El experimento que hemos propuesto asegura la formación de fractales si se trabaja con una pila de 1.5 V y permite obtener también dendritas si la pila es de 5 V (para la disolución menos concentrada).

Figura 20. Depósitos de cinc en una celda circular. (a) fractal; (b) homogéneo; (c) dendrítico; (d) filiforme (Fotos: Guillermo Sosa).

Figura 21. Diagrama de fase para los depósitos de cinc. Las estructuras tipo fractal crecen a valores bajos de voltaje (V). La concentración (c) está medida en moles de sulfato de cinc por litro de solución (1 mol de ZnSO₄ tiene una masa de 161.4 g)

El que se forme una estructura fractal o un depósito cristalino está condicionado por muchos factores: las características del transporte de iones en disolución, los mecanismos de transferencia de carga en los electrodos y las propiedades particulares del sólido formado (Voss, 1985); el papel que desempeña cada uno de ellos no es del todo claro. El tipo de sal con el que se trabaja es también de gran importancia: las sales de cobre y cadmio sólo permiten obtener estructuras fractales y homogéneas, mientras que las sales de plata dan lugar a hermosas formas de todos los tipos (véanse las imágenes a color).

Cosas tan simples como la geometría de la celda de electrodeposición pueden influir sobre los diferentes regímenes de crecimiento; no es lo mismo trabajar con una celda circular que con una rectangular. Cuando el experimento que antes describimos se repite en una celda rectangular se genera un pequeño mundo artificial poblado de arbustos, hongos, flores y árboles enanos (Figura 22). De nuevo, ¿cómo explicamos todo esto?

Figura 22. Depósitos de cinc en una celda rectangular. (a) fractal; (b) homogéneo, (c) dendrítico (Fotos: Guillermo Sosa).

AL AZAR Y DE UNO EN UNO

Alrededor de 1981, L. M. Sander y T. A. Witten (Witten, 1981, 1983) propusieron un mecanismo para explicar el crecimiento de agregados fractales y lo denominaron agregación limitada por difusión (o DLA, por sus siglas en inglés). La idea central consiste en reconocer que la difusión de partículas en el medio es el factor más importante que condiciona y limita la formación del agregado.

En este modelo, el proceso de crecimiento se inicia suponiendo la presencia de una partícula o un conjunto de ellas (cúmulo) que actúa como semilla para el desarrollo posterior. Adicionalmente, se considera que una gran cantidad de partículas se difunden hacia el cúmulo siguiendo una caminata al azar; una ruta en la que el tamaño y la dirección de los pasos se elige aleatoriamente. Cuando una partícula entra en contacto con el cúmulo se adhiere a él de manera permanente, y así el agregado crece a través de un mecanismo irreversible.

Las características de este modelo, en el que se repite siempre el mismo esquema: partículas que se difunden siguiendo una ruta aleatoria y se pegan al agregado al entrar en contacto con él, hacen que sea fácil utilizar a la computadora para simular el crecimiento (véase el capítulo "Para la computadora"). 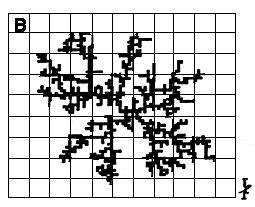El resultado que se obtiene aun después de depositar pocas partículas ( 900) es similar al que se muestra en la figura 23, donde vemos el caso de una celda circular (A) y una rectangular (B). El parecido con las formas fractales producidas a través del experimento de electrodeposición electroquímica (Figuras 20 (a) y 22(a)) es sorprendente, y se hace más obvio cuando se comparan con la simulación de un depósito que contiene un número mucho mayor de partículas (véanse las láminas ).

 

Figura 23. La simulación computacional por el método DLA genera estructuras fractales como éstas. (a) celda circular; (b) celda rectangular.

La estructura final está repleta de salientes y entrantes que son resultado de la presencia de lo que se denomina inestabilidades ante crecimiento. Cuando en el cúmulo se forma una protuberancia por azar, ésta crece más rápidamente que el resto del sistema pues la probabilidad de que las partículas se encuentren con ella es mayor; las partículas se pegan a la saliente y no alcanzan las regiones internas que ya no pueden rellenarse. Sobre la protuberancia en crecimiento se generan otras, y sobre éstas otras, y sobre las nuevas... hasta terminar con un objeto muy ramificado.

Estos fractales son autosimilares sólo en un sentido estadístico, ya que la ampliación de una de sus partes quizá no se parezca a la forma original, pero sí a algún otro agregado obtenido al repetir de nuevo el proceso de crecimiento. Para calcular su dimensión y verificar si es fraccional se sigue un procedimiento distinto al que analizamos en detalle casi al comienzo de este libro.

Cuando una estructura es muy irregular y no es formalmente autosimilar, su dimensión fractal se calcula normalmente por el método de la caja. El resultado que se obtiene también nos da una idea de la capacidad real del objeto para cubrir el espacio en el que está embebido. La manera de proceder es muy sencilla:

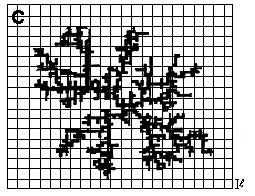
Se toma la estructura de interés y se coloca en una caja de lado L, sobre la que se construye una red regular en la que cada segmento tiene una longitud l (Figura 24(a)). Se cuenta el número de cajas que contienen alguna parte de la estructura, lo que da un número N. Ahora se repite el procedimiento utilizando redes cada vez más finas (l más pequeña, (Figuras 24(b) y 24(c)) registrando en cada caso la N que les corresponda. Cuando hacemos esto sobre una figura como la que aquí nos interesa es posible construir una tabla como la siguiente, en la que se registra el número de cajas que caben a lo largo del segmento L (L/l) y, del total de cajas en toda la red, sólo cuántas de ellas (N) atraviesan la figura:

L/l	5	10	20
-------------------------------------------------------------------------
N	18	52	148

Si se toma el logaritmo de ambas cantidades y se grafica log (N) vs log (L/l (Figura 24(d)), es posible ajustar sobre los datos una línea recta cuya pendiente es la dimensión fractal d_c de la figura. En realidad, esto nos indica que existe una relación del tipo:

N = (L/l)d_c

entre las dos variables, muy similar a la que ya describimos al hablar de la dimensión de Hausdorff.

 

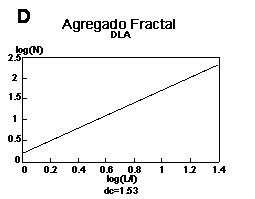Figura 24. Cálculo de la dimensión fractal del agregado DLA por el método de la caja. En este caso L=10 cm y (a) L/l=5, N=18; (b) L/l=10, N= 52; (c) L/l= 20, N=148. La pendiente de la recta en (d) en una medida de la dimensión fractal d_c.

El método de la caja es uno de los más utilizados en ciencias para obtener la dimensión de un objeto, pues ofrece un camino sistemático aplicable a una gran diversidad de formas naturales. También se usa para estudiar figuras que se encuentran en un espacio de tres dimensiones, y se utiliza para hacer las primeras estimaciones sobre la dimensión de objetos tales como costas, nubes, fronteras, sistemas arteriales, etcétera.

Para el agregado fractal que genera la computadora, la dimensión fractal, siguiendo el método de la caja, resulta cercana a 1.5, y es independiente de los detalles del proceso de agregación. Su valor es similar al que se ha obtenido para muestras experimentales (Matsushita, 1984; Argould, 1988) a pesar de la gran idealización del modelo de agregación limitada por difusión. La coincidencia en verdad es sorprendente; sólo pensemos que mientras en la simulación se depositan unos cuantos miles de partículas, en el experimento real se trabaja con miles de millones de átomos.

Cuando la simulación computacional se modifica para permitir que las partículas que chocan con el agregado puedan "rebotar" antes de adherirse, la estructura final es más compacta y simula un depósito homogéneo. Su dimensión sigue siendo fraccional, pero ya es muy cercana a 2.

El modelo de agregación limitada por difusión no es sólo de utilidad para analizar la estructura de depósitos electroquímicos. Parece ser que cuando se aplica una diferencia de potencial sobre una emulsión fotográfica o en la superficie de un aislante, se genera una descarga eléctrica cuyo patrón, llamado figura de Lichtenberg, es muy similar al fractal DLA. El caso se repite al estudiar el comportamiento de líquidos inmiscibles que son forzados a fluir uno a través del otro.

DEDOS VISCOSOS

Cuando un fluido como el agua o el aire se desplaza a través de un líquido más viscoso, la interfase entre ellos puede deformarse y generar dedos o estructuras más complejas. Este hecho no es nuevo para los ingenieros petroleros, químicos o geólogos que trabajan en procesos de extracción en mantos petrolíferos. Por ejemplo, en algunas ocasiones el material por recuperar queda atrapado en el subsuelo poroso y no puede ser extraído de manera directa; para desplazarlo es común bombear agua desde la superficie. Si en las condiciones de trabajo se forman dedos o conos de un líquido dentro del otro, la eficiencia de la extracción de reduce considerablemente pues el agua se dispersa en el petróleo.

Este fenómeno puede reproducirse a pequeña escala haciendo uso de un dispositivo muy simple desarrollado alrededor de 1898 por Henry Hele-Shaw (Walker, 1987):

Se toman dos placas de vidrio o acrílico de 1.5 cm de espesor, y 40 x 40 cm² de área. Se colocan horizontalmente una sobre otra y se sostienen con pinzas y soportes a unos 30 cm de la mesa de trabajo (Figura 25).

Sobre la placa superior se practica una perforación central de aproximadamente 0.2 cm de diámetro, a través de la cual se inyectarán los líquidos de interés. La separación entre las placas se controla utilizando tiras de masking-tape superpuestas y situadas en el contorno de la placa inferior; el propio peso de la placa superior y la presión ejercida por las pinzas de sostén, aseguran que su valor se mantiene constante a lo largo del experimento (entre 0.03 y 0.08 cm). Con el fin de mejorar la visualización de los patrones de flujo resulta conveniente introducir una lámpara de luz difusa entre las placas y la base.

En este experimento el líquido más viscoso o fluido por desplazar se inyecta o esparce entre las placas, generando una capa homogénea, y el líquido desplazante (agua normalmente) se inyecta por el orificio central.

 

Figura 25. Esquema de la celda de Hele-Shaw utilizada para estudiar patrones de flujo.

Cuando el fluido por desplazar es un material viscoso como salsa catsup, leche de magnesia, jarabe para la tos o miel de abeja (Córdoba, 1993) y el líquido inyectado es tinta azul o negra, los patrones de flujo adquieren formas diversas (Figura 26) que de nuevo se parecen a los electrodepósitos fractales y homogéneos. ¿Qué está sucediendo ahora?

a	b
c	d

Figura 26. Patrones de flujo al inyectar tinta azul en medios viscosos distintos. (a) Salsa catsup; (b) jarabe para la tos; (c) miel de abeja; (d) leche de magnesia (Fotos : Guillermo Sosa).

También en este caso existen inestabilidades ante crecimiento. Para comprenderlo mejor imaginemos una celda de Hele-Shaw en la que los fluidos presentes exhiben una interfase idealmente plana. Si en estas circunstancias se aplica una presión constante y uniforme sobre el fluido menos viscoso, la interfase se desplazará sin deformarse. Sin embargo, la presencia de cualquier perturbación que curve la superficie dará lugar a una diferencia de presiones y se incrementará la velocidad de flujo en esa zona (Figura 27). Si se mueve más rápido, se deforma más, si se deforma más, se mueve más rápido, y así de nuevo se generan protuberancias que crecen y se ramifican, pues cualquier protuberancia dentro de otra se mueve más rápido y ramifica, y...

Figura 27. Cualquier perturbación de la interfase entre ambos líquidos puede generar un dedo viscoso.

La evolución del patrón depende de varios factores, entre los que sobresalen (Robinson, 1985): la separación entre las placas, las viscosidades de los fluidos y la tensión interfacial. La influencia de este último parámetro es particularmente importante pues su presencia tiende a estabilizar y aplanar la interfase (recordemos que la tensión interfacial es una medida del costo energético de formación de la misma).

El trabajo teórico y experimental sobre los patrones de flujo en la celda de Hele-Shaw ha demostrado que la formación de estructuras fractales tipo DLA se favorece si:

—se incrementa la diferencia de viscosidades entre los fluidos,

—se disminuye la separación entre las placas o

—se reduce la tensión superficial.

En todo caso, siempre hay que buscar que los efectos de cualquier perturbación en la interfase dominen sobre las tendencias estabilizadoras del sistema.

Las estructuras que aparecen en una celda de Hele-Shaw también se generan a través de simulaciones computacionales basadas en el modelo de agregación limitada por difusión (DLA). Los resultados que se obtienen directamente con un programa como el que hemos utilizado para la electrodeposición coinciden muy bien con el caso en el que la tensión interfacial entre los líquidos es prácticamente cero. Cuando esto no es así, hay que incluir la posibilidad de que las partículas reboten con el cúmulo antes de adherirse a él. Esto suaviza las estructuras y permite generar patrones menos ramificados y verdaderos dedos viscosos (Tang, 1985; Liang, 1986).

El estudio de fenómenos como éstos es de gran utilidad para comprender en qué circunstancias se favorece la aparición de formas fractales, y es parte del inicio para desentrañar el misterio de la aparición de muchas formas naturales. Sin embargo, falta mucho por hacer e investigar; hoy día no es fácil predecir cuál será la geometría de un objeto, a pesar de haber identificado los mecanismos de crecimiento que lo generan. Hay quien juzga que conocer las reglas de la geometría fractal resultará de gran utilidad para simplificar este trabajo; hay quien piensa lo contrario, que basta de juegos. ¿Se nos está acabando la imaginación o soñamos demasiado? ¿Seguimos la pista correcta o nos perdimos en el laberinto?

Fractales
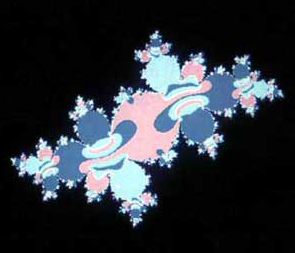
Figura 1.	Figura 2.
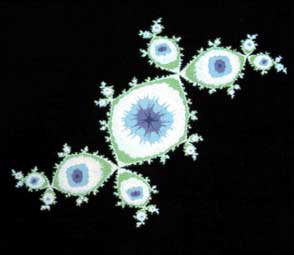
Figura 3.	Figura 4.
Figura 5.	Figura 6.
Figura 7.	Figura 8.
Figura 9.