VI. HUELLAS EN EL TIEMPO
LOS fractales no son solamente útiles para describir la geometría de las formas
naturales, también nos proveen de nuevas herramientas para analizar sus propiedades
dinámicas, la manera en que se desarrollan y evolucionan, o cómo interaccionan
entre sí para competir u organizarse. Los fractales son sin duda alguna parte
fundamental del nuevo lenguaje de la complejidad y el caos, y uno estaría tentado
a decir que habitan en esa frontera tan sutil entre el orden y el desorden.
Hay quien dice que están dentro del espejo que separa al reino del caos del
dominio de la organización y la estructura (Briggs, 1990); aparentemente están
ahí, sus reflejos se multiplican.
Los seres humanos siempre nos hemos preocupado por buscar las leyes que rigen la evolución del mundo que nos rodea. Se ha establecido así un conjunto de relaciones que nos permiten predecir el futuro de un sistema si se tiene información confiable sobre su estado presente o pasado. Estas reglas que le señalan a cada sistema el camino a seguir, se denominan deterministas y pueden ser simples o complejas; de ellas, en principio, se espera siempre una fidelidad absoluta, una capacidad predictiva sin límite.
Sin embargo, en los últimos años, gracias al desarrollo de las computadoras y de mejores métodos numéricos para resolver los problemas, se ha encontrado que existen sistemas que,
IMPORTANTE:a pesar de estar gobernados por relaciones
precisas y bien conocidas (sus ecuaciones determintstas), presentan
un comportamiento absolutamente ñIMPREDECIBLE! (Crutchfield,
1986). |
Esta característica es una propiedad intrínseca del sistema que no se evita acumulando más información y, sorprendentemente, su presencia es más una regla que la excepción. El fenómeno ya se ha observado en el estudio de movimientos planetarios, la predicción del clima, el crecimiento de cristales, la evolución de sistemas fisiológicos, algunas reacciones químicas, etcétera.
Perder la capacidad de predecir el futuro a largo plazo es un verdadero desastre,
es el CAOS, y el problema fundamental radica en la estructura de
las ecuaciones deterministas que le corresponden a cada sistema. Cuando un sistema
físico se comporta de manera continua y regular, de tal forma que su respuesta
a cualquier perturbación es siempre proporcional a la intensidad de la misma
(poco -> poco; mucho -> mucho), se dice que es un sistema lineal pues
la representación gráfica de su comportamiento dará lugar a una línea recta.
Si esto no es así, el sistema resulta no lineal y las cosas pueden complicarse.
Muchos sistemas no lineales exhiben un comportamiento caótico porque son muy sensibles a las influencias externas. Su susceptibilidad en ocasiones raya en la histeria: si, por ejemplo, quisiéramos predecir la trayectoria de una bola de billar que choca con otras en su camino, bastaría ignorar el efecto gravitacional de un electrón situado en la frontera de nuestra galaxia para comenzar a obtener resultados erróneos después de un minuto de haberla lanzado. Es también famoso el denominado efecto mariposa en la predicción del clima: en algunos modelos utilizados en climatología, no considerar el simple aleteo de una mariposa puede tener consecuencias desastrosas sobre la predicción del comportamiento atmosférico.
Un sistema caótico resulta impredecible porque es extraordinariamente sensible a la especificación de las condiciones iniciales a partir de las cuales se quiere estudiar su evolución (Dresden, 1992); cualquier pequeño cambio en el estado inicial tiene dramáticos efectos sobre el comportamiento futuro. Para predecir el fenómeno se necesitaría conocer los datos iniciales con precisión infinita, así como un control extremo del proceso; esto es imposible, independientemente de qué tanto logremos mejorar nuestros aparatos de medición y control, y de qué tan bien conozcamos las relaciones matemáticas que rigen su comportamiento.
Muchos sistemas son capaces de tener un comportamiento regular o caótico, de acuerdo con las condiciones a las que estén sujetos; desgraciadamente, no existen reglas generales que permitan decidir a priori si exhibirán o no una dinámica caótica. El tránsito entre el orden y el caos puede darse de manera brusca o gradual y esto cambia de sistema a sistema. Sin embargo, cuando se da, el resultado es increíble.
Ahora, ¿qué tienen que ver el caos y los fractales? Como muestra basta un ejemplo.
Imaginemos que estamos decididos a estudiar el comportamiento de una población de insectos en una isla y para ello desarrollamos el siguiente modelo (Davies, 1987):
La evolución de la población de insectos depende del ritmo de nacimientos y muertes que se presenten en su comunidad. Si suponemos que estos animales tienen un periodo de reproducción anual y la población en el año i era Ni, es de esperar que la población al año siguiente Ni+1 sea proporcional a la que había el año anterior. Esto es:
donde a es una constante de proporcionalidad que mide la capacidad reproductiva de la especie.
En la relación anterior no hemos tomado todavía en cuenta el efecto de la muerte de los insectos. Como primera aproximación podríamos decir que el mayor número de decesos se da por competencia entre individuos: compiten por el alimento, por la pareja, por territorio, etcétera; digamos que muy pocos se mueren de viejos. Entre más insectos haya, más difícil será que sobreviva cada uno, de ahí que no sea descabellado pensar que la probabilidad de que muera un individuo es proporcional a la población total de ese año: Ni. Como esto se vale para cada uno de ellos, el ritmo de decesos para toda la población será proporcional a Ni x Ni = N2i, o:
Si combinamos ambos efectos (nacimientos menos muertes) resulta la ley de crecimiento poblacional que esperamos:
Esta relación es muy útil, pues si damos valores a las constantes a y b, y elegimos una población inicial No, con ello se calcula la población al año siguiente N1. Con el resultado se genera N2, que a su vez nos lleva a obtener N3 y así sucesivamente. Este proceso es de nuevo una iteración que nos permite analizar la evolución de la población año con año. El modelo de crecimiento poblacional es muy sencillo pero en él ya está presente un elemento que puede conducirnos a resultados inesperados. La iteración contiene un término en el que la variable Ni está elevada al cuadrado y esto quiere decir que tratamos con un sistema no lineal (la gráfica de la relación (aN - bN²) como función de N no es una línea recta).
Para facilitarnos un poco las cosas resulta conveniente suponer que las constantes a y b son iguales y que la población Ni está medida con respecto a una población máxima de referencia, por lo que su valor está siempre entre 0 y 1. Esto no altera las conclusiones finales pero facilita los cálculos que, por cierto, pueden hacerse directamente en una computadora (véase el capítulo "Para la computadora").
Cuando se analiza el valor de la población como función del tiempo que predice la iteración simplificada:
para diferentes valores del parámetro de crecimiento a, es posible distinguir varios casos:
a) Para valores de a menores que 1 la tasa de nacimientos es tan baja que la población decrece año con año y termina por extinguirse (Figura 28 (a)). Esto sucede siempre independientemente de cuál sea la población inicial.
b) En el intervalo de a entre 1 y 3, la población se estabiliza en un valor constante diferente de cero que no depende de la No de la cual se parte (Figura 28 (b)). El balance de nacimientos y muertes asegura que la población nunca cambie.
c) A partir de a>3, las cosas se complican. En cuanto el parámetro
de crecimiento es un poco mayor que tres, la población comienza a oscilar entre
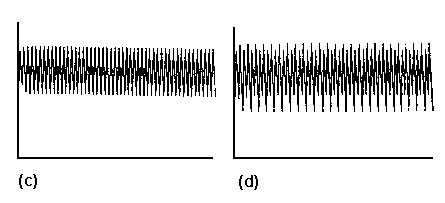
dos valores distintos (Figura 28(c))y se acostumbra decir que la solución antes
estable se bifurca, se generan dos posibilidades que se visitan alternadamente
en el transcurso de los años. Esta situación se mantiene hasta a 
3.4495, donde cada rama de nuevo se bifurca y la población oscila entre
cuatro valores diferentes (Figura 28 (d)) Si seguimos aumentando el valor de
a, el mismo esquema de duplicación se reproduce en cada rama y el periodo de
oscilación aumenta a 8,16, 32 (Figura 28 (e))..., hasta que en a
3.5699 el ciclo tiene una duración infinita. A partir de aquí, poco o nada es
predecible; el comportamiento se torna caótico (Figura 28 (f)) y la evolución
temporal es muy susceptible a la población inicial elegida. Por ejemplo, cuando
a4, una
diferencia de 0.000001 entre dos datos iniciales hace que los resultados sean
completamente distintos después de 50 iteraciones. En la región del caos la
población cambia año con año de una manera que desafía al mejor adivino.
![[MCT 45]](../img/147_82ab.gif) |
 |
 |
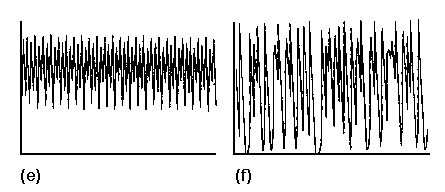Figura 28. Evolución de la población de insectos para varios valores del parámetro a. (a) a= 1.00; (b) a= 2.00; (c) a= 3.30; (d) a= 3.50; (e) a= 3.569; (f) a= 4.00.
La transición hacia el caos se ve más claramente cuando se grafica el valor o valores que alcanza la población a tiempos muy largos, como función del parámetro de crecimiento a. La gráfica que se genera se conoce como diagrama de bifurcaciones y se presenta en la figura 29 (a) (véase el capítulo ñPara la computadora" si hay interés en reproducirla). El diagrama muestra con claridad los valores de población que se visitan para cada valor de a: cuando es pequeño se tiene una sola rama (población constante), después dos (oscilación entre dos valores) y así seguimos hasta alcanzar la región caótica que tiene una estructura muy compleja.
En la zona del caos hay muchos valores de a para los que la población evoluciona sin seguir un orden determinado; sin embargo, también está repleta de secciones en las que se recupera el comportamiento periódico. Estas regiones aparecen como franjas más blancas y cuando hacemos una ampliación para analizarlas (Figuras 29(b) y 29 (c), nos deparan la tan esperada sorpresa. Dentro de ellas se repite el mismo esquema de bifurcaciones que en el diagrama general, y así ad infinitum, el caos y el orden se entremezclan siguiendo las reglas de la geometría fractal.
![[MCT 46]](../img/147_84.gif)
Figura 29. a) Diagrama de bifurcaciones para la dinámica poblacional N1+1= a*Ni(1-Ni). En (b) y (c) se presentan ampliaciones de la zona central en la franja blanca más ancha en la figura que las precede.
Es importante señalar que este último hecho no es una casualidad. El comportamiento general de nuestra dinámica poblacional es muy similar al que se encuentra cuando se analizan las ecuaciones que describen sistemas diversos: circuitos eléctricos, reacciones oscilantes, láseres o fluidos-turbulentos. En algunos de ellos la evolución temporal se representa en diagramas que grafican simultáneamente la posición y velocidad de las partículas que los constituyen. la estructura de las figuras que se generan depende de la condiciones de trabajo, pero si se identifica que su geometría es fractal, se tiene una señal indudable de que el sistema está comportándose caóticamente.
Los fractales parecen ser herramientas particularmente útiles para desentrañar los misterios del caos; es como si en su lenguaje la aparente extrañeza e irregularidad del comportamiento caótico fuera el estado natural. Quizás, de hecho, debíamos haber esperado su presencia. Ya hemos visto que muchos fractales son producto de realizar la iteración matemática de una función no lineal (z², por ejemplo); las leyes dinámicas que describen el comportamiento de diversos sistemas fisicos muchas veces no son más que eso. De ahí que los fractales aparezcan como sus huellas, únicas, indelebles, inconfundibles.
Los fractales son el prototipo de lo que uno estaría dispuesto a llamar un objeto complejo. No en el sentido de difícil o complicado, pues normalmente se generan a través de procedimientos sencillos, sino por el hecho de presentar detalle a toda escala, de guardar información a muy diferentes niveles. Nuestro Universo está plagado de objetos complejos, y él mismo, como los fractales, presenta estructuras organizadas a diversas escalas: cúmulos de galaxias, galaxias, estrellas, planetas, y por lo menos en nuestro planeta, nubes, montañas, organismos vivos. ¿De dónde salió todo esto?
Uno siempre se pregunta cómo surgió el Universo, pero con menos frecuencia se cuestiona cómo llegó a convertirse en lo que hoy conocemos. Si al principio de los tiempos, o mejor dicho, nuestros tiempos, el universo naciente carecía de forma y contenido, ¿qué lo llevó a organizarse? ¿Cómo lo hizo? En los últimos años estos cuestionamientos han comenzado a aclararse gracias al estudio de sistemas que, en condiciones adecuadas, tienen la capacidad de autorganizarse. Todos ellos comparten características comunes entre las que destacan: su habilidad para generar estructuras macroscópicas complejas y organizadas, su extrema susceptibilidad a las perturbaciones externas, y su increíble capacidad para autorregularse y funcionar como una entidad única que responde creativamente y se adapta a las condiciones del medio (Nicolis, 1989).
Los sistemas que se autorganizan siempre se encuentran en condiciones que los mantienen muy alejados de su estado de equilibrio; son entidades que están en contacto con el medio externo y utilizan la energía que éste les proporciona para organizarse y formar estructuras complejas. Es por ello que también se les denomina estructuras disipativas.
Un ejemplo típico de autorganización se presenta cuando una capa horizontal de algún fluido se somete a una diferencia de temperaturas. Para lograrlo basta calentar el líquido en su parte inferior o, aún más fácil, trabajar con un líquido volátil permitiendo que se evapore. Esto enfriará la superficie y provocará la diferencia de temperatura deseada. El fenómeno se presenta a gran escala cuando el Sol calienta la superficie terrestre y la atmósfera se toma como fluido de trabajo.
En este experimento, el líquido más caliente cercano a la base es menos denso y tratará de ascender; el más frío cercano a la superficie es más denso y tratará de descender. Si la diferencia de temperaturas es pequeña, la viscosidad del fluido impedirá su movimiento, pero si se sigue calentando se alcanza una condición crítica en la que repentinamente el líquido comienza a desplazarse y se organiza en celdas de flujo convectivo a las que se denomina celdas de Bénard (Figura 30 (a).
![[MCT 47]](../img/147_87a.gif)
Figura 30. (a) Esquema de la estructura de las celdas de Bénard en un corte lateral del fluido. (b) Estructura en la superficie de la acetona después de la formación de las celdas. (Foto: Guillemro Sosa).
El experimento es fácil de hacer (Talanquer, 1991):
| En un recipiente de fondo plano (como una caja de Petri) se coloca acetona hasta formar una capa de aproximadamente 0.3 cm de ancho. Se espolvorea sobre ella un poco de aluminio en polvo que sirve para hacer visible el movimiento de las partículas del fluido. Cuando se sopla sobre la superficie para acelerar la evaporación, es increíble ver cómo el sistema se autorganiza formando una multitud de celdas de convección (Figura 30(b)). |
Cuando aparecen las celdas de Bénard, el sistema que era originalmente homogéneo adquiere una verdadera estructura. En cada una de las celdas hay del orden de 1021 moléculas que se desplazan de manera concertada, a pesar de su movimiento térmico azaroso. Esto quiere decir que de alguna forma se ha establecido comunicación entre ellas.
La aparición de los patrones de Bénard en un fluido es un fenómeno completamente reproducible. Si se aseguran las mismas condiciones de trabajo, las celdas se presentarán al alcanzar la misma diferencia de temperatura. Sin embargo, su posición o el sentido en el que rota el líquido dentro de ellas es algo impredecible e incontrolable. Sólo el azar determina cómo será el patrón en cada caso.
Esta posibilidad de elegir entre muchas opciones y de que el azar decida cuál se selecciona es típica de sistemas que se autorganizan. Se acostumbra decir que el sistema es arrastrado hasta un punto en el que repentinamente se le presentan muchos caminos, pero es imposible predecir cuál seguirá. El resultado de la selección puede conducirlo a un nuevo estado más complejo y organizado, pero también puede perderlo en el reino del caos. Loque es indudable es que se trata de un mecanismo muy efectivo para explotar la creatividad del sistema, generando formas complejas muy parecidas pero no idénticas.
Otros ejemplos de sistemas con capacidad de autorganizarse se presentan en casos tan distintos como la producción de rayos láser, la aparición de flujos turbulentos, las reacciones químicas oscilantes o la formación de ondas químicas (Talanquer, 1992). Al igual que en el caso de las celdas de Bénard, la descripción de su comportamiento incluye términos como selección, coherencia, creatividad, organización, adaptación. Esto ha abierto las puertas hacia el campo de la biología, y hoy resulta que modelos muy semejantes se utilizan para estudiar el desarrollo embrionario, los procesos de diferenciación y localización celular, la propagación de impulsos nerviosos o la formación de órganos multicelulares.
Los modelos propuestos para estudiar estos fenómenos son de diversos tipos, pero dentro de ellos existe una familia que ha resultado particularmente útil y su uso se ha generalizado. Se les llama autómatas celulares y es aquí donde, de nuevo, nos invaden los fractales.
Los autómatas celulares fueron utilizados por primera vez por los matemáticos John von Neumann y Stanislaw Ulam en 1948 para representar la reproducción en algunos sistemas biológicos. Posteriormente, su uso se extendió a diversos campos y hoy día sus aplicaciones son muy variadas.
Para construirlos basta tomar un arreglo de sitios o celdas, cada una de las cuales se encuentra en un estado que se caracteriza por la asignación de un valor numérico. Por ejemplo, si sólo hay dos estados posibles: vivo-muerto, vacío-lleno, etcétera, pueden elegirse los números 0 y 1 para distinguirlos.
Una vez elegido un estado inicial para todo el sistema se procede a estudiar cómo evoluciona en el tiempo. Para ello se definen reglas que establecen cómo cambia el estado de cada celda, considerando su situación y la de sus vecinos más cercanos en la etapa anterior.
Un caso sencillo se presenta cuando consideramos un autómata celular unidimensional en el que cada celda puede estar ocupada por un organismo vivo (1) o estar vacía (0). Si la distribución inicial es al azar; una representación esquemática del sistema se vería de la siguiente manera:
![[MCT 48]](../img/147_89a.gif)
Las reglas de evolución temporal que podemos proponer son múltiples. Por ejemplo:
| Cada organismo vivo sobrevivirá para la siguiente etapa si y sólo si no lo rodean por ambos lados otros organismos vivos (esto podría representar la competencia). En un sitio vacío aparece un organismo vivo (nacimiento) si al menos un vecino es un organismo vivo. |
En términos numéricos esta regla de evolución podría esquematizarse considerando la suma de los números asignados a cada celda y sus dos vecinos más cercanos. La suma tomaría valores entre 0 (todos vacíos) y 3 (todos llenos), y el estado para la siguiente etapa se obtendría consultando una tabla como la siguiente:
|
Si la suma da Nuevo
estado
|
ññññññññññ ||
|
0
|
®
|
0
|
|
1
|
®
|
1
|
|
2
|
®
|
1
|
|
3
|
®
|
0
|
Cuando la regla se aplica a cada celda del sistema inicial se genera la población de la siguiente etapa. Después el procedimiento se repite una y otra vez, y para fines de análisis resulta conveniente dibujar uno tras otro los resultados que se obtienen:
![[MCT 49]](../img/147_89b.gif)
En la práctica este trabajo puede hacerlo sistemáticamente una computadora (véase el capítulo "Para la computadora") y el esquema de evolución después de 100 etapas, por ejemplo, es como el que se muestra en la figura 31 (a). En esta figura se distinguen los sitios llenos de los vacíos por la asignación de color blanco o negro.
 |
 |
 |
 |
Figura 31. Patrones de evolución de una autómata celular. (a) y (b) corresponden a la regla de crecimiento descrita en el texto; (c) y (d) muestran el resultado para reglas distintas.
De nuevo, el resultado es fascinante. A pesar de haber partido de una situación azarosa y de que la regla de evolución actúa muy localizadamente (sobre una celda y sus dos primeros vecinos), el autómata celular es capaz de generar espontáneamente un patrón complejo que presenta organización y estructura a toda escala. Esto es, el sistema se autorganiza.
Las características del patrón que se forma se distinguen más claramente cuando se repite el cálculo suponiendo que inicialmente sólo había un organismo vivo situado en una celda central. El resultado de la evolución del autómata (Figura 31(b)) es nada más y nada menos que una estructura muy similar al ñtriángulo de Sierpinski! La autorganización del sistema conduce a la formación de una estructura compleja, autosimilar y con dimensión fraccional. Fractales, fractales, fractales.
Si la regla de evolución se modifica, la estructura del patrón puede cambiar drásticamente (Figuras 31(c) y 31(d)), pero en general sólo se identifican unos cuantos tipos generales. Hay reglas que conducen a patrones fractales o a estructuras periódicas; otras no llevan a nada o generan estructuras de tamaño finito. Las condiciones iniciales pueden modificar ciertos detalles pero no la esencia del resultado.
El ejemplo que hemos presentado es un caso sencillo y quizá poco realista si pretendemos representar el comportamiento de un sistema fisico. Sin embargo, las ideas generales pueden extenderse para generar autómatas en dos y tres dimensiones que reproducen notablemente bien las propiedades de muchos sistemas complejos. El reto al utilizarlos consiste en capturar la esencia del fenómeno y traducirla al lenguaje del autómata. Considerando un mayor número de estados para cada celda y diferentes reglas de evolución, los autómatas celulares efectúan la mimesis de la formación de ondas químicas, el flujo de fluidos a través de obstáculos, o el crecimiento de copos de nieve. Cuando se introducen ciertos elementos aleatorios en las reglas que rigen su comportamiento, son modelos adecuados para fenómenos tales como la propagación de enfermedades infecciosas o de incendios en un bosque, la difusión de líquidos a través de medios porosos o la distribución de cierta especie de plantas en una selva (Peterson, 1988).
Detrás de muchos de los resultados obtenidos siguen apareciendo los fractales como la elección más eficiente para generar estructuras complejas, como la alternativa más creativa, como obsesión inevitable.
